核能与核技术应用的飞速发展导致放射事故的潜在危险日益增加,对辐射损伤伤员的快速分析提出了新的需求和挑战。双着丝粒染色体分析作为生物剂量估算的金标准,目前主要依赖于人工分析[1]。为了增加剂量估算的可信度,要分析的分裂相多,需要耗费大量人工资源[2-3]。近年来,一些发达国家的辐射细胞遗传学实验室已装备了自动分析系统[4-8]。市场上也有较成熟的产品,比如德国蔡司公司的Metafer玻片扫描系统、美国昂飞公司的CytoScan HD细胞遗传学检测系统等。但是这些国外产品价格都比较昂贵,动辄上百万。国内在该领域起步较晚,染色体自动分析尚处于研究阶段。特别是在辐射生物领域,还局限于半自动双着丝粒分析估算剂量[9]。为此,本文基于人工智能技术,开展了国内自主研发的用于生物剂量估算的双着丝粒体自动识别算法初步研究,以期助力提高生物剂量估算效率。
材料与方法1.材料:染色体图像来自于中国疾病预防控制中心辐射防护与核安全医学所制备的标准片,共1 471张,均为灰度图像。本研究基于美国MathWorks公司发布的MATLAB R2021b软件进行算法开发。
2.图像预处理:受染色体标准片制备过程中染料质量不稳定、分布不均匀,以及成像系统噪声被放大等因素的影响,导致染色体图像引入一定数量的噪声,从而影响双着丝粒染色体的自动识别精度。本研究将采用5×5模板的中值滤波算法对图像进行预处理,消除椒盐噪声,并保护图像的边界信息。
3.阈值分割与二值化处理:随机选择50张图像作为输入样本,采用OTSU算法求得分割阈值。OTSU算法作为一种自动的无参数无监督的分类算法,对图像有很强的自适应性[10]。将图像进行从上到下,从左到右的扫描;如果像素值大于或等于分割阈值,那么将该像素的灰度值设为255;否则,设为0。从而将图像中染色体与背景分离。
4.染色体标记:为了识别双着丝粒染色体,确定哪一条染色体有双着丝点,因此需对图像中的染色体进行标记。本研究采用八连通区域标记算法[11]。在染色体二值图像中,相互连通的白像素(像素值为255)集合成为一个区域。通过对每个区域进行标记操作,求得图像中区域的数目。首先按照图像扫描的原则,依次检测每个像素,如果发现某像素点像素值为255,则依次检测该点的左上、正上、右上及左前点共4个点的像素值,进行连通性判断,并标记。
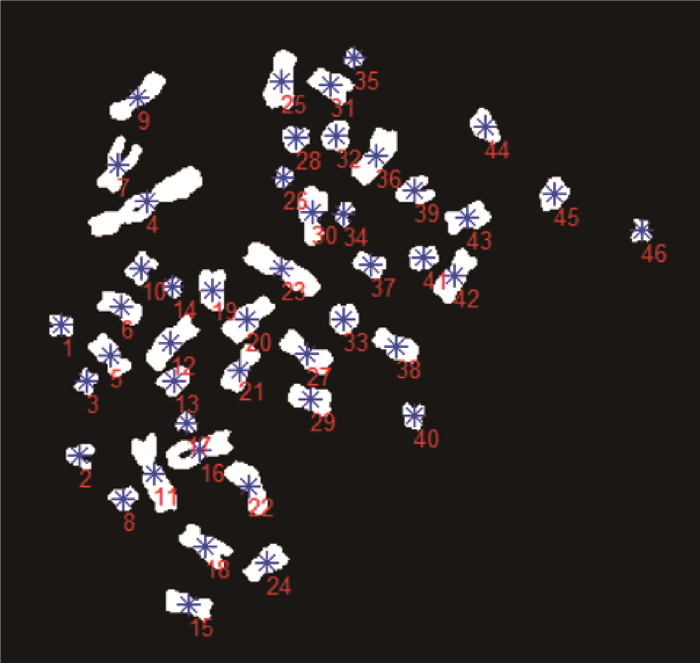
由于前文处理方法不能将图像中的噪声全部清除,有些噪声也被标记为区域,因此需要对被标记的噪声进行删除。每个连通区域进行尺度检测,当染色体尺寸少于400个像素时,无法形成可识别的双着丝粒体;而最大的染色体尺寸也不超过1 920个像素。因此,根据上述原则,消除小尺度的噪声块和所有大尺度的噪声球,标记结果如图 1所示。图像中的连通区域都具有唯一且连续的标记值,标记值的最大值为图像连通区域的数目。
|
图 1 染色体连通区域标记结果 Figure 1 Chromosome labeling results |
5.卷积神经网络算法:由于存在分离、交叉、粘连等现象,一个连通区域既可能是一个染色体,也可能是半个染色体,还可能是多个染色体。双着丝粒体检测只是针对包含一个染色体的连通区域,对于包含多或半个染色体的连通区域将会产生许多错检,应预先删除。本研究将选择训练两个微型的卷积神经网络[12-13]来实现这个功能。首先,训练一个微型卷积神经网络识别仅包含1个染色体的连通区域,然后,训练另一个微型卷积神经网络识别包含多个或半个染色体的连通区域。只有被第一个网络识别且被第二个网络拒绝的连通区域,才被认为是候选染色体。
因标记的训练数据集较少,而且用于训练和识别的图像块比较简单,所以卷积神经网络的结构很小。因为图像中染色体的分辨率差别不大,因此这两个神经网络的卷积层仅需10个尺度的卷积核,池化层采用最大值采样。由于网络规模很小,层间权值采用全连接。在训练数据较少的情况下,直接采用随机初始化网络权值的效果不佳。所以本研究先用其他的二分类图像对随机初始的网络权值进行预训练,再用训练数据集对其进行二次训练。输出图像块分类的结果如图 2所示。对于连通区域为半条或多条染色体的图像块进行丢弃;对连通区域为一条染色体的图像块,则作为候选染色体。

|
A.连通区域为半条染色体;B.连通区域为一条染色体;C.连通区域为多条染色体 图 2 输出图像块分类结果 A. Connected region includes half a chromosome; B. Connected region includes one chromosome; C. Connected region includes multiple chromosomes Figure 2 Classification results of output image blocks |
6.双着丝点识别算法
(1) 染色体旋转:为方便双着丝点的识别,本研究将候选染色体进行适度旋转预处理,调整候选染色体均处于几乎相同角度,利于后续统一检测处理。具体实现过程为:首先测量每个候选染色体图像块的长度和宽度,计算候选染色体的倾斜角度θ,然后采用最近邻插值将该图像块旋转-θ°,使得全体图像块中的候选染色体均处于近似水平的状态。染色体旋转示意图如图 3所示。

|
A、C. 原图像块;B、D. A和C旋转后图像块 图 3 染色体旋转示意图 A, C. Original image block; B, D. Image block after A and C rotation Figure 3 Schematic diagram of chromosome rotation |
(2) 确定着丝点:考虑到用确定性函数不适用于准确判断双着丝粒染色体,本算法将基于模糊逻辑理论,定义模糊隶属度函数来描述每个染色体属于双着丝粒染色体的程度。双着丝粒染色体模糊隶属度函数是由多个特征的模糊隶属度函数组成,将所有子特征模糊隶属度值相乘得到该染色体模糊隶属度值,如式(1)所示。按照文献[14-15]定义隶属度的方式,本研究定义3个模糊隶属度函数f1(x)、f2(x) 和f3(x) 分别描述着丝点的位置、宽度和染色体的尺度特征,并综合形成了双着丝粒体的模糊隶属度函数F(x)。
| $ F(x)=\prod\limits_{i=1}^{n} f_{i}(x) $ | (1) |
对于每个候选染色体图像块,分别提取候选染色体的上背景和下背景,分别统计它们在每个坐标点的高度ht(n) 和hb(n), 其中n为像素横坐标值,ht(n)、hb(n) 为像素纵坐标值。红色区域为候选染色体的上背景,蓝色区域为候选染色体的下背景,白色区域为候选染色体,黑色区域为候选染色体内的间隙,如图 6所示。
|
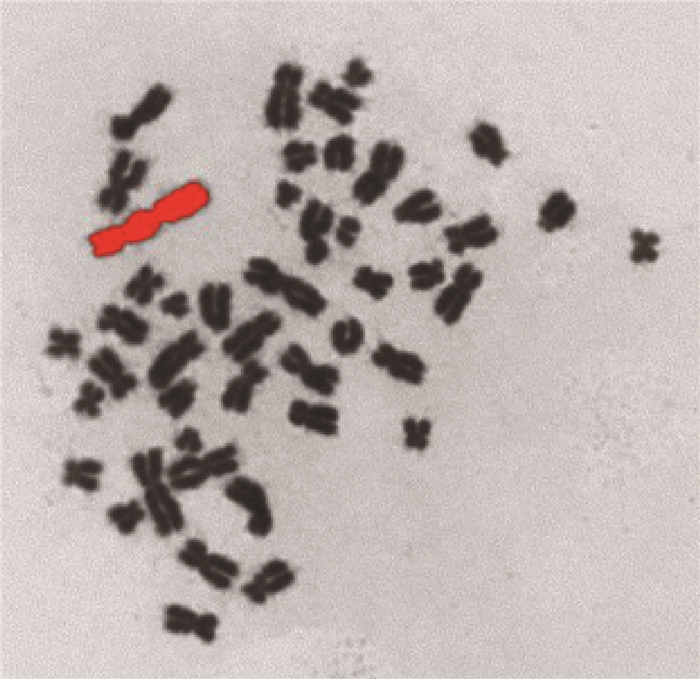
注:红色为识别出的双着丝粒染色体 图 4 双着丝粒染色体识别结果 Figure 4 Dicentric chromosome identification results |

|
图 6 染色体区域划分示意图 Figure 6 Schematic diagram of the division of chromosome regions |
按照公式(2)和公式(3)对高度值ht(n) 和hb(n) 进行加权模糊:
| $ \begin{gathered} h_{t}(i-2)+h_{t}(i-1) \times 2+h_{t}(i) \times 4+ \\ h_{t}(i+1) \times 2+h_{t}(i+2)=H_{t}(i) \\ \end{gathered} $ | (2) |
| $ \begin{gathered} h_{b}(i-2)+h_{b}(i-1) \times 2+h_{b}(i) \times 4+ \\ h_{b}(i+1) \times 2+h_{b}(i+2)=H_{b}(i) \end{gathered} $ | (3) |
分别求Ht(i) 和Hb(i) 的极值点,作为染色体的候选着丝点。真实的染色体着丝点两侧必定存在着上、下背景的峰值点,必然存在着相互配对的Ht(i0) 和Hb(i1) 极值点与之对应,且两坐标i0和i1之间的距离非常小。本研究定义染色体着丝点的模糊隶属度函数f1(x),如公式(4)所示:
| $ f_{1}(x)=\mathrm{e}^{-\frac{\left|i_{0}-i_{1}\right|}{2}} $ | (4) |
Ht(i0) 和Hb(i1) 按照i的值顺序匹配,若遇一配多或者是多配多的情况,则能使模糊隶属度函数f1(x) 取得极大值的i0和i1值,被认定为染色体着丝点的上、下背景极值点横坐标。当|i0-i1|≥6时该收腰点模糊隶属度f1(x) 的值< 0.05,为简化计算,本文设定距离阈值为6,只把距离小于阈值的着丝点被认定为候选着丝点,其余候选着丝点直接淘汰。可见,模糊隶属度函数f1(x) 约束了丝点在X方向上的位置。另外,判断染色体着丝点是否自然收腰,需确定Ht(i0) 和Hb(i1) 是否为递增式极值点。真实的双着丝粒体着丝点中的上、下背景极值点都是递增式极值点,突变式极值点一般是含噪声或变异的染色体。
为识别双着丝点,本研究定义了模糊隶属度函数f2(x) 来统一描述基于宽度(Y方向)特征的染色体收腰点属于着丝点的程度,如公式(5)、(6)所示:
| $\begin{gathered} f_{2}(x)=\mathrm{e}^{D\left(i_{0}, i_{1}\right)} \end{gathered} $ | (5) |
| $ \begin{gathered} D\left(i_{0}, i_{1}\right)= \\ -\frac{\left(\sqrt{\left(i_{0}-i_{1}\right)^{2}+\left(H_{\mathrm{t}}\left(i_{0}\right)+H_{\mathrm{b}}\left(i_{1}\right)-K\right)^{2}}-12\right)^{2}}{6} \end{gathered} $ | (6) |
式中,K是染色体图像块的高度。经计算,设定两极值点纵坐标Ht(i0) 和Hb(i1) 的高度差上限是15,下限是5,此时f2(x) 隶属度函数值近似为0.05。所有超出这个高度差范围的候选着丝点的f2(x) 均 < 0.05,直接排除这些候选着丝点。
在待检测图片中可能含有许多染色体粘连现象,两个单着丝粒染色体粘连一起容易被误认为是一个双着丝粒染色体。包含两个或多个染色体的粘连体尺度相对较大。因此,通过定义尺度模糊隶属度函数f3(x),来约束双着丝粒染色体的尺度大小,如公式(7)所示:
| $ f_{3}(x)= \begin{cases}0 & (x<400) \\ \frac{x-400}{760} & (400<x \leqslant 1160) \\ \frac{1900-x}{760} & (1200<x \leqslant 1920) \\ 0 & (x>1920)\end{cases} $ | (7) |
式中x是染色体的像素数。经计算,设定尺度上限是1 882,下限是438,所有超出这个尺度范围的染色体的f3(x) 隶属度函数值均 < 0.05。
因此,选择0.000 125作为着丝点的隶属度函数F(x) 的阈值, 所有超过阈值的候选点均被认为是着丝点,所有包含2个着丝点的图像块均被认为是含有双着丝粒染色体的图像块。
结果为了验证本研究所提的双着丝粒体识别算法的实际效果,应用上述算法对1 471张染色体图像进行了测试。首先,对1 471张染色体图像进行了人工识别,其中有92张图像包含双着丝粒体(97个双着丝粒体)。然后,使用该算法进行识别,共检出81张图像,其中有65张图片包含双着丝粒体(68个双着丝粒体), 错检16张图片,漏检27张。对应的双着丝粒体细胞检出率为70.7%,误检率为19.8%,漏检率为29.3%。部分识别结果如图 4所示。结果表明,算法在双着丝粒染色体自动识别方面具有良好的效果,为双着丝粒染色体自动识别提供了一种可靠、有效的方法。
讨论双着丝粒染色体自动分析生物剂量估算方法不仅能估算急性均匀照射,还可以估算局部照射和慢性照射剂量,适用于大规模核与辐射事故下快速高通量的生物剂量估算[16]。双着丝粒染色体自动分析生物剂量估算方法应用的关键是实现双着丝粒染色体的快速准确识别。染色体的尺度不一,且存在弯曲、联结、交叉、断裂等多种变形,难以找到单一特征用来准确判断染色体是否为双着丝粒体。因此,本研究组合染色体的多种图像特征联合检测,能够提高检测结果准确率。本研究基于卷积神经网络、模糊逻辑等算法,实现了双着丝粒染色体识别算法的初步研究。应用结果表明,算法对双着丝粒体染色体细胞检出率达到70.7%,可以大大节约剂量估算分析人员的时间,提高双着丝粒染色体的识别效率,为实现快速高通量的生物剂量估算提供了可能。
然而,算法双着丝粒染色体的检出率受以下因素的影响:①受图像质量影响较大。染色体制片效果直接影响染色体的图像质量,而在实际操作中获得高质量的制片并不容易。由于受染色体制片质量的影响,有时候染色体形态过度细长或短粗、分散不良时,双着丝粒染色体检出率较差。②当图像中黏连染色体数目较少时,检出率较高;反之,较差。③受训练样本数量影响。本研究使用的1 471张染色体图片中,阳性图片只有92张。应用人工智能技术训练获得性能良好的模型,需要大量的训练样本,一般应达到上万、百万这样的数量级。④受算法本身误差传递的影响。在本文所提算法中深度神经网络先对图像块进行预筛选,删除交叉、粘连和断裂的染色体,能够降低算法的误检率。在图像处理的过程中,前面步骤产生的误差会向后传递,算法本身的误差对于双着丝染色体识别有一定的影响,在清晰的高分辨图像中算法的误差极小可忽略不计,但是在质量较差的模糊图像中算法的误差会变大,降低目标识别精度。
在今后的工作中,将针对上述问题需要做更多的研究,进一步优化算法,改善算法性能,提高算法的效率和强度;收集更多的训练样本,构建人工确认的双着丝粒染色体图形特征库,优化模型,提高双着丝粒染色体的检出率;将算法在大型染色体数据库上进行检验,以期为双着丝粒染色体全自动分析快速高通量的剂量估算方法研究提供更多的科学依据。
利益冲突 无
作者贡献声明 范胜男负责算法研究、软件开发以及论文撰写;邓君负责算法研究、论文修改和指导;张子扬参与算法研究和讨论;阮健磊和潘艳负责染色体标本制备和图像采集;孙全富负责论文撰写的指导
| [1] |
International Atomic Energy Agency. Cytogenetic dosimetry: application in preparedness for and response to radiation emergencies[R]. Vienna: IAEA, 2011.
|
| [2] |
白玉书, 陈德清. 人类辐射细胞遗传学[M]. 北京: 人民卫生出版社, 2006. Bai YS, Chen DQ. Human radiation cytogenetics[M]. Beijing: Peoples's Medical Publishing House, 2006. |
| [3] |
中华人民共和国卫生部. GB/T 28236-2011染色体畸变估算生物剂量方法[S]. 北京: 中国标准出版社, 2011. The Minister of Health of the People's Republic of China. GB/T 28236-2011. Method of chromosome aberration analysis for biological dose assessment[S]. Beijing: Standards Press of China, 2011. |
| [4] |
Vaurijoux A, Gruel G, Pouzoulet F, et al. Strategy for population triage based on dicentric analysis[J]. Radiat Res, 2009, 171(5): 541-548. DOI:10.1667/RR1664.1 |
| [5] |
Li Y, Shirley BC, Wilkins RC, et al. Radiation dose estimation by completely automated interpretation of the dicentric chromosome assay[J]. Radiat Prot Dosim, 2019, 186(1): 42-47. DOI:10.1093/rpd/ncy282 |
| [6] |
Royba E, Repin M, Pampou S, et al. RABiT-Ⅱ-DCA: a fully-automated dicentric chromosome assay in multiwall plates[J]. Radiat Res, 2019, 192(3): 311-323. DOI:10.1667/RR15266.1 |
| [7] |
吕玉民. 染色体畸变在急、慢性辐射损伤评估中的意义专家解析[J]. 中国辐射卫生, 2019, 28(4): 349-354, 360. Lyu YM. Expert interpretation on the significance of chromosomal aberration in the assessment of acute and chronic radiation damage[J]. Chin J Radiol Health, 2019, 28(4): 349-354, 360. DOI:10.13491/j.issn.1004-714X.2019.04.001 |
| [8] |
韩林, 陆雪, 李杰, 等. 双着丝粒体半自动与人工分析估算生物剂量的比较研究[J]. 中华放射医学与防护杂志, 2020, 40(11): 826-831. Han L, Lu X, Li J, et al. Study on the comparison of semi-automatic and manual dicentric detection for biological dosimetry[J]. Chin J Radiol Med Prot, 2020, 40(11): 826-831. DOI:10.3760/cma.j.issn.0254-5098.2020.11.003 |
| [9] |
王平, 韩林, 李杰, 等. 双着丝粒染色体分析在核与辐射事故应急生物剂量估算中的应用与进展[J]. 辐射防护通讯, 2020, 40(4): 97-102. Wang P, Han L, Li J, et al. Application of dicentric chromosome analysis in nuclear/radiation emergency biodosimetry and its progress[J]. Radiat Protect Bull, 2020, 40(4): 97-102. DOI:10.3969/j.issn.1004-6356.2020.04.023 |
| [10] |
Nobuyuki OTSU. A threshold selection method from gray-level histograms[J]. IEEE Trans Syst, 1979, 9(1): 62-66. DOI:10.1109/TSMC.1979.4310076 |
| [11] |
杨淑莹. VC++图像处理程序设计. 2版[M]. 北京: 清华大学出版社, 北京交通大学出版社, 2005: 163-169. Yang SY. VC++ image processing program design. 2nd edition[M]. Beijing: Tsinghua University Press, Beijing Jiaotong University Press, 2005: 163-169. |
| [12] |
Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks[C]//Neural information processing systems foundation. advances in neural information processing systems 25 (NIPS 2012). Stateline, Nevada: NIPS, 2012: 1097-1105.
|
| [13] |
Sharma M, Saha O, Sriraman A, et al. Crowdsourcing for chromosome segmentation and deep classification[J]. 2017 IEEE Conference on computer vision and pattern recognition workshops. IEEE, 2017, 34-41. DOI:10.1109/CVPRW.2017.109 |
| [14] |
Ferro A, Brunner D, Bruzzone L. Automatic detection and reconstruction of building radar footprints from single VHR SAR images[J]. IEEE Trans Geosci Remote Sens, 2013, 51(2): 935-952. DOI:10.1109/TGRS.2012.2205156 |
| [15] |
Huang Y, Liu F. Detecting cars in VHR SAR images via semantic CFAR algorithm[J]. IEEE Geosci Remote S, 2016, 13(6): 801-805. DOI:10.1109/LGRS.2016.2546309 |
| [16] |
戴宏, 刘玉龙, 冯骏超, 等. 双着丝粒染色体自动分析生物剂量估算研究[J]. 中华放射医学与防护杂志, 2017, 37(3): 182-186. Dai H, Liu YL, Feng JC, et al. Study on the automatic analysis of dicentric chromosome biodosimetry[J]. Chin J Radiol Med Prot, 2017, 37(3): 182-186. DOI:10.3760/cma.j.issn.0254-5098.2017.03.004 |
 2022, Vol. 42
2022, Vol. 42


