放射性核素内照射治疗是一种将放射性核素或其标记物引入人体后使其在病变组织或器官浓集,利用放射性核素发射射线的辐射效应抑制和破坏病变组织的治疗方法。该治疗方式又可分为放射性核素受体靶向治疗、放射性核素基因介导治疗、放射性核素反义治疗等[1],在甲状腺癌、唾液腺癌、前列腺癌以及甲状腺功能亢进等疾病的治疗中具有广泛的应用前景[2-3]。随着我国《医用同位素中长期发展规划(2021—2035年)》[4]的不断推进,放射性核素内照射治疗在我国的临床应用必将得到更快和更广的普及。
诸多研究表明,放射性核素内照射治疗的剂量与疗效之间存在显著的正相关关系,但其副作用也不容忽视,需要在疗效和安全性之间找到平衡[5-6]。放射性核素内照射治疗的个体化剂量估算通常需要分两个步骤:先获得放射性核素的分布情况及该核素在肿瘤靶区和危及器官等感兴趣区域的累积活度分布;接着计算蓄积在患者体内的放射性核素衰变时发射出各类射线在患者体内感兴趣器官或组织的能量沉积(吸收剂量)。本文重点围绕这两个方面的方法学研究进展进行综述。
一、放射性核素的体内分布与蓄积放射性核素在患者体内的分布与蓄积过程直接关系到患者肿瘤靶区和危及器官/组织的累积活度。借助体外成像等手段,可较准确地掌握治疗用放射性核素在患者体内的定量分布。
1. 患者体内放射性核素分布测量:早期主要通过测量患者血液或尿液样品中的放射性核素活度来间接估算放射性核素在患者体内的蓄积量[7]。之后甲状腺131Ⅰ测量仪和伽马相机等辐射测量设备的出现,使得131Ⅰ等具有伴生可成像光子的放射性核素体内分布的直接测量成为了可能。基于影像数据的个体化内照射剂量计算在放射性核素内照射治疗的效果评估中具有重要意义[8-9]。
自21世纪后期以来,随着单光子发射计算机体层成像(SPECT)和正电子发射计算机体层成像(PET)的发展,已可实现大部分治疗用放射性核素在患者体内的三维分布测量[10]。当前,临床常规SPECT设备的空间分辨率普遍在6~11 mm,通过改进准直器设计及超分辨率重建算法还可提升空间分辨率,部分研究已实现可达亚毫米级分辨率的局部成像(如0.5 mm人脑成像)[11];临床常规PET设备的空间分辨率通常为4~5 mm,部分新型临床设备(如搭载2.76 mm晶体的PET系统)通过改进探测器设计,可将美国电气制造商协会(NEMA)标准分辨率提升至2.8 mm,并借助算法优化实现1.0 mm的局部高分辨率[12]。
为进一步提高核医学成像的分辨率并反映出亚细胞尺度肿瘤组织的异质性,近年来,多模态成像、人工智能(AI)和影像组学等技术已应用于核医学图像处理[13-14]。磁共振成像(MRI)具有极高的空间分辨率,但对于PET/MRI系统,MRI图像并不能直接显示物质对光子的衰减性质。为此,Ladefoged等[15]借助深度学习的方法建立了MRI信号与计算机体层成像(CT)中HU值的对应关系,并依此进行了图像的衰减校正。上述核医学成像技术的发展,已为具有伴生可成像光子的放射性核素内照射治疗剂量估算打下坚实的基础。然而,对于通常不具有伴生可成像光子的α核素内照射治疗,目前的体内成像技术仍难以准确定量其体内分布[16]。
2. 感兴趣器官/组织的累积活度计算:虽然治疗用的放射性核素通常都具备靶器官特异性,但仍有相当大一部分核素也会随人体的代谢,蓄积到骨髓、肾、肝等具有一定辐射敏感性的器官或组织中,产生有害的不良反应;另一方面,患者的年龄、性别、生理与病理等情况的不同也会导致摄入的放射性核素在感兴趣器官中不同的活度分布变化。为此,需要使用多个时间点的体内成像测量,通过函数拟合和积分得到长时间的累积活度。时间-活度曲线的拟合常使用多指数求和的模型进行拟合:
| $ A(t)=\left(\sum\limits_{i=1}^{M} a_{i} \mathrm{e}^{-\lambda_{i} t}\right) \cdot \mathrm{e}^{-\lambda_{p} t} $ | (1) |
式中,M为求和的指数项个数,ai;λi为待定的拟合参数(λi> 0);λp为核素的物理衰变常数[17]。要注意的是,为避免过拟合,参数个数必须少于测量次数。另一方面,为获得更加准确的活度信息,诸多研究表明,SPECT或PET图像的定量在重建过程中还需要对射线的衰减、散射和小病灶或器官的部分容积效应所产生的偏差做适当校正[18-19]。
对于噪声较大、指数拟合不稳定的情形,也可以使用简单的梯形法,通过直线连接各个测量点,并对最后一个测量点利用物理半衰期进行外推的方式进行累积活度计算。通常,基于物理半衰期而忽略生物代谢的外推会一定程度上高估累积活度[20]。对于仅进行一次测量的情形,Hänscheid等[21]给出了一种在活度单指数衰变的简单假设下基于单次测量结果的累积活度计算方式。这种近似方法利用在0.75~2.5个有效半衰期内的一次测量,可以得到不依赖有效半衰期的较为有效的累积活度估计。
体内测量难以获得活度信息时,生物动力学模型和药代动力学模型也可用于估算放射性核素在人体中的分布和转运情况。前者基于相关实验观察到的药物浓度变化,给出经验性的器官和组织水平的平均药物浓度估计,其隔室之间的转运系数可作为测量结果的拟合参数;后者基于对潜在生理过程的理解,对药物浓度变化的估计可精确到亚细胞水平[22],其转运系数由对相关的生理和药理学参数的了解推出[23]。
放射性核素内照射治疗药物的生物动力学模型通常用隔室模型描述。它可表示为一系列描述不同器官或组织之间转运效率的微分方程[24]:
| $ \frac{\mathrm{d} A_{i}}{\mathrm{~d} t}=\sum\limits_{j \neq i} A_{j} \lambda_{j i}-A_{i}\left(\sum\limits_{j \neq i} \lambda_{i j}+\lambda_{p}\right) $ | (2) |
式中,Ai、Aj分别为i、j隔室中的总活度;λji为j隔室向i隔室的转运系数;λp为核素的物理衰变常数。各个隔室之间的转运系数λji为描述隔室模型的主要参数。
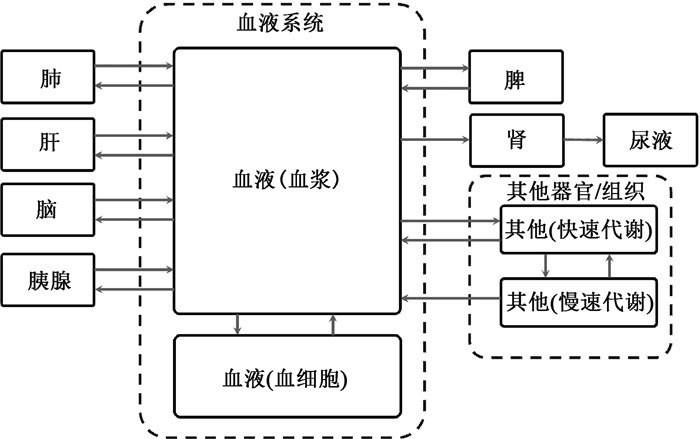
一个典型的生物动力学隔室模型如图 1所示。隔室模型方程组的解是指数函数求和的形式。因此,时间-活度曲线的拟合中常用多指数函数模型。
国际放射防护委员会(ICRP)在其相关出版物[26-30]中给出了多种常见核素的生物动力学模型及相关参数。该模型给出了较简单离子形态131Ⅰ,223Ra等核素的生物动力学模型,可以作为这些治疗用核素生物动力学模型的基础[31-32]。治疗用生物动力学模型的建立需要大量患者体内活度-时间变化的临床数据;在临床数据难以取得的情况下,可对动物实验得到的代谢参数进行适当缩放得到人体代谢的估计[33]。
生物动力学模型只关心器官或组织的平均活度。对于短射程以及具有明显靶向性的核素,需使用基于生理学的药代动力学(physiologically based pharmacokinetic,PBPK)模型精确模拟药物沉积位点的分布。与一般的生物动力学模型类似,PBPK模型的主体仍然是表示各个组织器官的隔室[34]。不同的是,PBPK模型中每个隔室不仅考虑隔室之间的输运性质,也考虑隔室内部药物的吸收、分布、代谢和排泄过程。不同于主要用于辐射防护目的的生物动力学模型,PBPK模型建立的初衷即为进行前瞻性的药物疗效分析[35]。目前已报道有一些用于放射免疫疗法和放射配体疗法的PBPK模型[36-37]。
二、内照射剂量计算内照射剂量评估研究工作始于1959年ICRP对待积吸收剂量概念的提出。1968年,美国核医学与分子影像学会(SNMMI)核医学内照射剂量委员会(MIRD)在其发布的第1号Pamphlet(手册)[38]中,首次提出以器官累积活度和器官比吸收分数为核心的内照射剂量估算方法,由此确立了系统的核医学内照射剂量计算体系。之后,核医学成像与计算体模的发展又为基于上述方法的内照射剂量估算提供了更加准确的手段。近年来,为更准确地反映α粒子和俄歇电子等短射程粒子在细胞以至DNA尺度的能量沉积与生物学效应关系,微剂量学计算方法也得到了一定发展。
1. 宏观尺度的内照射剂量计算:宏观尺度的内照射剂量计算主要基于MIRD框架。早期方法受限于计算机技术和医学影像精度,主要进行器官层面的平均剂量估算。MIRD框架的核心是计算靶区的平均吸收剂量D(rT),其计算公式如下[39]:
| $ \begin{gathered} D\left(r_{\mathrm{T}}\right)=\sum_{r_{\mathrm{S}}} N\left(r_{\mathrm{S}}\right) \sum_{R, i} E_{R, i} Y_{R, i} \cdot S A F\left(r_{\mathrm{S}} \rightarrow r_{\mathrm{T}}, R, i\right) \\ =\sum_{r_{\mathrm{S}}} N\left(r_{\mathrm{S}}\right) \cdot S\left(r_{\mathrm{S}} \rightarrow r_{\mathrm{T}}\right) \end{gathered} $ | (3) |
式中,D(rT)为靶区rT的平均剂量;N(rS)为源区rS的累积活度,即发生的核素衰变次数;ER, i、YR, i分别为衰变产生的R种类射线第i个能峰的能量及其分支比;SAF(rS→rT, R, i)(Specific Absorbed Fraction,比吸收分数)为单位能量的源区粒子在靶区中的平均剂量期望;S(rS→rT),即源区到靶区的S值,为源区中核素一次衰变在靶区rT产生的平均剂量期望。
(1) 传统的S值计算方法:为便于计算与使用,将人体简化为一系列表示不同组织、器官的简单几何体(如圆柱体、椭球体)的程式化体模被早期的诸多研究用于统一化的辐射剂量计算,这些研究将大量S值的计算结果列表给出[40]。近年来,随着体素化体模和网格化体模等仿真程度更高的体模的相继出现[41-42],器官层面S值计算的精确性得到了很大提升。依其个性化程度,S值计算使用的体模可分为四个等级:基于人群中位数身高和体重信息的参考人体模,基于典型身高和体重组合的参考人体模库,仅配准患者身体轮廓的个体化体模,以及能描述患者身体和器官轮廓的个体化体模[20]。
另外,考虑到患者身体结构的个体化差异,由参考人体模得到的S值还可以根据患者的器官质量进行修正。在核医学内照射剂量计算领域,通常只需利用下式修正对剂量贡献最大的源区同时作为靶区的自身S值:
| $ S_{\mathrm{self}}^{\prime}=S_{\mathrm{self}} \cdot \widetilde{m}^{R} $ | (4) |
式中,Sself、S′self分别为考虑器官质量校正前、后的自身S值;
器官S值的计算结果通常用于危及器官吸收剂量的安全性评估,通常不适用于肿瘤靶区治疗剂量计算。另外,器官S值计算假定核素在器官水平上均匀分布,当器官水平的非均匀沉积情况对剂量及辐射效应影响较大时,还需要使用亚器官水平的S值进行更精细的计算。例如,在开展肾毒性评估时,大分子药物主要聚集于肾髓质中的肾小管尖端,而小分子药物主要与皮质中的肾小管中部结合,这为药物的肾脏内分布赋予了一定的异质性[20]。为此,MIRD的第19号小册子中给出了一个年龄相关的肾脏亚器官模型及其S值[45]。
(2) 基于剂量点核的体素S值计算方法:随着核医学成像技术的发展和更为精细的体素化体模的出现,相比传统的器官S值,更加精确的基于剂量点核的体素S值计算方法也得到了发展。传统的器官S值计算假定放射性核素在源区均匀分布,不能充分利用核医学图像提供的放射性核素分布细节信息,其剂量计算在小尺度下的准确性难以保证。
剂量点核(dose point kernel, DPK)是各向同性点源在均匀介质中单次衰变产生的剂量分布期望,因其球对称性而可表示为一个一维的剂量-距离曲线。将该剂量点核与活度分布进行卷积,可简便地得到体素水平的剂量分布。但是,剂量点核作为一种连续的、球对称的分布,它在体素化几何中的卷积面临较大的计算代价。为此,体素S值(voxel S value,VSV)方法应运而生。体素S值是体素化几何中的剂量点核,可由蒙卡模拟或直接对剂量点核进行体素化重采样得到,常以一个三维数组的形式表示。体素化几何下体素S值的卷积计算过程可利用快速傅里叶变换进行加速,这也是体素S值方法作为一种体素化几何中的快速剂量计算方式被提出的初衷[46]。
基于剂量点核的体素S值方法也存在一些固有缺点。点核方法假设粒子始终在均匀介质中传输,如果粒子在真实的输运中所经介质种类发生变化,计算结果就会产生偏差。这对骨髓、肺等密度变化剧烈区域的小尺度剂量计算是不利的。为此,Khazaee等[47]提出了一种使用VSV核中相邻体素剂量之比进行校正的方法。另外,体素S值的计算代价正比于介质种类和粒子能量的组合数,在多种介质中模拟各个能量的粒子输运较为耗时费力。VSV方法最初仅针对水或软组织计算单一介质的点核,依此卷积计算全身的剂量分布[46];近来,已有不少研究人员[48-49]创建的多重VSV方法,这种方法通过在多种不同密度介质中分别计算VSV核,之后与不同密度体素的活度分布分别卷积,最后将结果相加,从而更加妥善地考虑人体异质性对剂量分布的影响。
(3) 直接蒙特卡罗模拟计算方法:近年来,随着计算机硬件算力的大幅提升、减方差技术的发展和计算机中央处理器或图像处理器并行计算加速等技术在蒙特卡罗模拟计算软件中的引入,早期因其较大的时间代价而较少使用的直接蒙特卡罗模拟的内照射剂量计算时间已降至数分钟的量级[50]。这使得基于直接蒙特卡罗模拟的剂量计算方法进入临床剂量学评估成为了可能。通过融合SPECT/CT、PET/CT等医学影像数据,构建患者特异性模型,精准反映组织密度、放射性核素浓度等参数,可准确计算出患者的肿瘤靶区和危及器官的个体化吸收剂量。该方法已被多个国家推荐为放射性核素内照射治疗药物临床评价技术指导原则的标准化工具。
作为剂量计算的金标准,患者个体化体模中的蒙特卡罗模拟可以最为细致地考虑患者特异的解剖结构和粒子的输运细节;对于非均匀的介质,复杂的几何结构和未达成带电粒子平衡的情形都可以做到准确的剂量计算[22]。上述S值和剂量点核方法重点关注剂量沉积的期望值,难以考虑剂量分布的统计涨落。这使得微尺度剂量计算更加依赖直接蒙卡模拟的方法。若无须考虑其算力成本,直接蒙特卡罗模拟计算具有最高的准确性和最广的适用范围。
(4) 基于人工智能的计算方法:作为图像处理领域的一大有力工具,人工智能技术主要在以下两方面为内照射剂量计算提供助益:首先,可通过深度学习方法处理SPECT/CT、PET/CT等医学影像数据,实现靶区和危及器官中放射性核素分布的高精度三维重建[51];其次,可尝试以卷积神经网络(CNN)、生成对抗网络(GAN)等网络架构利用蒙特卡罗算法得到的计算结果进行训练,得到迅速且较为可靠的内照射剂量估计。Lee等[52]使用卷积神经网络对68Ga射程内的局域PET图像进行处理,得到了与直接蒙卡结果较为一致的体素剂量分布;Ma等[53]利用机器学习方法成功预测了接受177Lu-PSMA I&T治疗前列腺癌患者的内照射剂量。
(5) 内照射剂量计算软件:近年来,国外已开发出了数十款可用于核医学治疗内照射剂量估算的软件系统[54],大多数软件仍以MIRD剂量计算框架为基础进行开发。OLINDA/EXMⓇ(其前身为MIRDOSEⓇ)是一款最广泛应用于核医学成像与治疗剂量计算的软件[55]。该软件分为OLINDA(organ level internal dose assessment)和EXM(exponential modeling)两部分,前者使用MIRD剂量框架进行器官剂量评估,后者使用指数拟合的方式计算累积活度分布。OLINDA/EXMⓇ可支持超过1 000种不同的核素,OLINDA经常作为其他内照射剂量计算软件的验证工具。对于接受103Pd或 90Y植入或栓塞治疗的患者,RMDPⓇ、RAY doseⓇ和Simplicit90YⓇ等软件系统均可支持图像的自动分割与配准,可以准确估算肿瘤靶区的吸收剂量,这些软件均已通过了美国FDA的批准,并于加拿大等国投入临床使用。Voximetry TorchⓇ作为一款侧重于使用GPU加速技术进行内照射剂量估算的软件,其器官分割、配准和时间-活度曲线拟合,以及粒子输运的蒙特卡罗模拟过程都支持GPU并行计算加速,该软件于2022年取得了美国FDA批准。
2. 微观尺度的内照射剂量计算:对于短射程核素的剂量-效应关系的评估,微剂量学计算是必要的。电离辐射与物质的相互作用是一个随机过程,其相互作用次数和各次相互作用的能量转移是随机变量。在应用α核素与俄歇电子核素开展内照射治疗时,α粒子和俄歇电子等短射程核素因其LET很高,射程很短(表 1),宏观的吸收剂量不再是评价其治疗效果的唯一指标。需要进行微剂量学计算,使用比能(z,Gy)或线能(y, keV/μm)[56]等微剂量学量在细胞模型中评估其生物学效应。比能反映靶区受到辐射作用的强弱,其频率加权的平均值为吸收剂量;线能反映辐射粒子与物质相互作用空间上的密集程度,其频率加权的平均值为传能线密度。比能和线能是随机变量,它们的完整数学描述需给出概率分布函数。
|
|
表 1 不同粒子在人体中的典型LET与射程[57] Table 1 Typical LET and range of different particles in the human body[57] |
为获得细胞或亚细胞水平的S值,Goddu等[58]计算了同一细胞中不同细胞器之间的S值;小尺度的辐射生物学效应与细胞群的密度、细胞的形态和核素在细胞中的沉积位点密切相关[56],为精确评估辐射与细胞及分子的相互作用,Vaziri等[59]开发的MIRDcellⓇ软件可进行细胞群微观结构的建模与剂量评估。目前,Geant4-DNA软件对DNA碱基级别的结构也有细致的描述[60]。不同于宏观尺度的剂量学,为正确描述间接作用对DNA分子的损伤,微剂量学的蒙特卡罗模拟不仅要模拟粒子输运的物理过程,也要模拟辐射引发自由基的生成和自由基造成DNA损伤等化学过程。
三、剂量与效应关系放射性核素治疗内照射剂量估算的主要目的是为了评估其疗效和副作用。因此,建立辐射剂量与生物学效应的关系有重要的科学意义和应用价值。在放射治疗领域,人们常用线性二次模型(linear-quadradic model,LQ model)来描述吸收剂量(D)与细胞存活分数(survival fraction, SF)的关系[57]:
| $ S F=\mathrm{e}^{-\alpha D-\beta D^{2}} $ | (5) |
式中,线性项系数α描述单个辐射事件对单个细胞的直接影响,非线性项系数β描述两个辐射事件对同一个细胞的协同影响。
考虑到外照射治疗和内照射治疗通常都是分次进行,分次治疗会使得同样大的剂量产生的辐射效应有所减弱,因此学术界又引入生物有效剂量(biologically effective dose,BED)来修正分次照射的剂量与效应关系[61]:
| $ S F=\left(\mathrm{e}^{-\alpha d-\beta d^{2}}\right)^{n}=\mathrm{e}^{\left[-\alpha D\left(1+\frac{d}{\alpha / \beta}\right)\right]}=\mathrm{e}^{-\alpha \operatorname{BED}} $ | (6) |
式中,D为总吸收剂量,假设照射等分为n次进行,d为单次吸收剂量,D=nd;理论上,BED数值上等于以无穷小的分次剂量给药(这种方式下β项不会产生任何作用)达到同样生物学效应所需的剂量。
另一方面,不同于外照射放疗,内照射治疗用放射性核素会在患者体内滞留数天至十数天之久,其间放射性活度在达到高峰后会因代谢和物理衰变不断减少,且肿瘤体积的变化也会使得靶区的S值随时间发生变化。因此,需要结合时间-活度曲线计算不同时间点靶区的吸收剂量率Ḋ(t)[22]:
| $ \dot{D}\left(r_{\mathrm{T}}, t\right)=\sum\limits_{r_{\mathrm{S}}} A\left(r_{\mathrm{S}}, t\right) \cdot S\left(r_{\mathrm{S}} \rightarrow r_{\mathrm{T}}, t\right) $ | (7) |
式中,A(rS, t),S(rS→rT, t)分别为随时间变化的源区活度与随时间变化的源区到靶区S值。内照射核素在滞留期间同样会受到DNA的自身修复作用的影响。为此,Lea和Catcheside[62]提出了用于对β项做进一步修正的G(T)因子。该因子数值上等于T时段内造成一次辐射损伤后第二次辐射到来时该损伤未被修复的概率的期望:
| $ G(T)=\frac{2}{D^{2}} \int_{0}^{\mathrm{T}} \dot{D}(t) \mathrm{d} t \int_{0}^{t} \dot{D}(\tau) e^{-\mu(t-\tau)} \mathrm{d} \tau $ | (8) |
式中,D为累积吸收剂量;T为施加剂量的总时间(通常取为正无穷);μ为DNA修复因子,即一个单链断裂事件单位时间内被修复的可能性,可通过体外实验取得。因此,单次给药情形下细胞存活分数SF和生物有效剂量BED的表达式需要分别修正为:
| $ S F=\mathrm{e}^{-\alpha D-G(T) \beta D^{2}}=\exp \left[-\alpha D\left(1+D \cdot \frac{G(T)}{\alpha / \beta}\right)\right]=\mathrm{e}^{-\alpha \mathrm{BED}} $ | (9) |
需要提及的是,计算G(T)因子需要获得整个时间序列的剂量率-时间曲线而不仅是累积剂量,这给实际应用带来了不便。为此,通常假设活度随时间以有效衰变常数λ单指数衰减,时段T取为+∞,依此计算单次给药情形下G(+∞)以及BED:
| $ G(+\infty)=\frac{\lambda}{\lambda+\mu} $ | (10) |
| $ \mathrm{BED}=D\left(1+\frac{D}{\alpha / \beta} \cdot \frac{\lambda}{\lambda+\mu}\right) $ | (11) |
为描述组织异质性对内照射生物学效应的影响,研究人员又引入了等效均匀生物有效剂量(equivalent uniform biologically effective dose,EUBED)来评价组织中剂量分布不均匀性的细胞平均存活分数SF[63-64]:
| $ \text { EUBED }=-\frac{1}{\alpha} \ln \left(\frac{1}{N} \sum\limits_i \mathrm{e}^{-\alpha \mathrm{BED}_i}\right) $ | (12) |
| $ \overline{\mathrm{SF}}=\frac{1}{N} \sum\limits_i \mathrm{e}^{-\alpha \mathrm{BED}_i}=e^{-\alpha \mathrm{EUBED}} $ | (13) |
式中,N为体素总数;BEDi为体素i的生物有效剂量。
剂量-效应关系的评估是放射性核素内照射治疗疗效评估的重要环节。尤其对于内照射放疗与外照射放疗结合使用的情形[57],以及考虑核素相对生物学效应差别较大的衰变产物的情形,合理的内照射剂量-效应评估具有十分重要的意义。
四、小结与展望综上所述,放射性核素内照射治疗的剂量估算是一个相当复杂的过程。尽管目前已构建了较为完备的内照射剂量计算框架,且可以借助一些商用软件系统结合核医学的定量成像来开展个体化内照射剂量计算,内照射剂量学走进临床核医学治疗应用仍面临诸多挑战,其主要问题及可能的解决方法如下:
首先是影像数据定量精度的限制。内照射剂量计算的本质是活度-时间-空间积分的求解。受限于显像设备的定量性能,对于ml量级的肿瘤转移灶,现有技术还难以实现亚器官/组织尺度的活度刻画。多模态影像的融合与影像组学的使用有望改善这一问题。如将SPECT、PET与MRI、CT的功能/解剖信息融合,可提升靶区勾画与剂量计算的准确性。影像组学通过提取纹理特征等参数,可帮助构建更精细的肿瘤生物动力学模型。基于AI的图像增强方法可以降低图像噪声,增强影像质量,从低质量影像中提取高保真活度分布信息。这种方法有望成为进行肿瘤异质性建模的主要手段。
其次是现有的成像模式占用资源多且成本高。为定量患者体内放射性核素的分布及其变化情况,目前主要使用多次SPECT或PET成像来动态监测患者体内的放射性核素分布情况,其临床推广受限于高昂的设备成本和复杂的操作流程。患者通常需在数天至十数天内多次接受显像检查,会严重消耗设备机时、住院床位等医疗资源,且难以确保患者的依从性。针对这一挑战,有必要开展放射性核素内照射治疗的PBPK模型研究,以期利用PBPK模型来替代耗时耗力的成像。结合AI技术对患者影像数据的增强,还有望进一步降低显像频次。
再次是目前α核素治疗患者的体外成像仍面临较大困难,即便能找到合适的替代显像剂,α治疗核素的剂量-效应关系仍较难定量确定。为此建议先加强微剂量学的计算方法研究与验证,进一步量化线能、比能等微剂量学参数,进而整合微剂量学数据与细胞生物学实验结果,完成由剂量到临床效应的跨尺度预测框架。
放射性核素治疗的内照射剂量估算的主要目标是预测治疗效果及其安全性,并为个体化治疗提供用药方案。由以上主要问题和可能的解决方案可以看出,未来的内照射治疗剂量学是迈向精准化与智能化的新一代剂量学。这一发展愿景的实现需要大量的算力与数据资源的支撑,需在以下几个方面实现突破:第一,建立AI赋能的自动化剂量计算平台,开发集成影像分析、生物建模与剂量优化的AI系统,实现从显像到剂量报告的一站式处理;第二,依托基于GPU或CPU集群的并行计算技术与云端网络,增强本地或云端的算力调配,使基层医院能够使用高性能计算资源,为AI、蒙特卡罗模拟计算等高算力消费的技术提供算力支持;第三,建立涵盖物理剂量、微剂量参数与临床结果的多中心数据库,对珍贵的患者数据资源进行合理的共享,从而为AI训练与PBPK模型的建立提供至关重要的数据支持。
放射性核素治疗的内照射剂量学正经历从宏观到微观,从静态到动态的方法变革。随着AI、影像组学和并行计算技术的进一步引入,未来十分有希望实现剂量学指导的个体化给药治疗,最终推动核医学迈入真正的精准治疗时代。
利益冲突 无
作者贡献声明 綦家成负责综述撰写与文献整理;卓维海负责综述写作指导和修改;李俊豪负责图表制作以及文献资料的搜集与分析;汪景航负责文字语句的修改与勘误
| [1] |
医学名词审定委员会核医学名词审定分委员会. 核医学名词[M]. 北京: 科学出版社, 2018. Nuclear Medicine Subcommittee, China National Committee for Terminology in Science and Technology (Medical Division). Chinese terms in nuclear medicine[M]. Beijing: Science Press, 2018. |
| [2] |
Hu J, Li H, Sui Y, et al. Current status and future perspective of radiopharmaceuticals in China[J]. Eur J Nucl Med Mol Imaging, 2022, 49(8): 2514-2530. DOI:10.1007/s00259-021-05615-6 |
| [3] |
陈跃. 我国诊疗一体化核素及放射性药物临床应用与展望[J]. 协和医学杂志, 2022, 13(2): 187-191. Chen Y. Development and prospect of theranostic medical isotopes and radiopharmaceuticals in China[J]. Med J Peking Union Med Coll Hosp, 2022, 13(2): 187-191. DOI:10.12290/xhyxzz.2021-0557 |
| [4] |
国家原子能机构, 科技部, 公安部, 等. 医用同位素中长期发展规划(2021-2035年)[R/OL]. (2021-06-24)[2025-06-25]. https://nnsa.mee.gov.cn/ztzl/haqshmhsh/haqrdmyyt/202501/202501/t20250125_1101449.html. China Atomic Energy Authority, Ministry of Science and Technology of the People's Republic of China, Ministry of Public Security of the People's Republic of China, et al. Medium and long-term development plan for medical isotopes (2021-2030)[R/OL]. (2021-06-24)[2025-06-25]. https://nnsa.mee.gov.cn/ztzl/haqshmhsh/haqrdmyyt/202501/202501/t20250125_1101449.html.. |
| [5] |
Barone R, Borson-Chazot F, Valkema R, et al. Patient-specific dosimetry in predicting renal toxicity with 90Y-DOTATOC: relevance of kidney volume and dose rate in finding a dose-effect relationship[J]. J Nucl Med, 2005, 46(Suppl 1): 99-106. |
| [6] |
Mohan V, Bruin NM, van de Kamer JB, et al. The increasing potential of nuclear medicine imaging for the evaluation and reduction of normal tissue toxicity from radiation treatments[J]. Eur J Nucl Med Mol Imaging, 2021, 48(12): 3762-3775. DOI:10.1007/s00259-021-05284-5 |
| [7] |
Weber WA, Czernin J, Anderson CJ, et al. The future of nuclear medicine, molecular imaging, and theranostics[J]. J Nucl Med, 2020, 61(Suppl 2): 263-272. DOI:10.2967/jnumed.120.254532 |
| [8] |
Piwowarska-Bilska H, Kurkowska S, Birkenfeld B. Individualization of radionuclide therapies: challenges and prospects[J]. Cancers (Basel), 2022, 14(14): 3418. DOI:10.3390/cancers14143418 |
| [9] |
Strigari L, Konijnenberg M, Chiesa C, et al. The evidence base for the use of internal dosimetry in the clinical practice of molecular radiotherapy[J]. Eur J Nucl Med Mol Imaging, 2014, 41(10): 1976-1988. DOI:10.1007/s00259-014-2824-5 |
| [10] |
Crișan G, Moldovean-Cioroianu NS, Timaru DG, et al. Radiopharmaceuticals for PET and SPECT imaging: A literature review over the last decade[J]. Int J Mol Sci, 2022, 23(9): 5023. DOI:10.3390/ijms23095023 |
| [11] |
Ma T, Wei Q, Lyu Z, et al. Self-collimating SPECT with multi-layer interspaced mosaic detectors[J]. IEEE Trans Med Imaging, 2021, 40(8): 2152-2169. DOI:10.1109/TMI.2021.3073288 |
| [12] |
Singh MK. A review of digital PET-CT technology: Comparing performance parameters in SiPM integrated digital PET-CT systems[J]. Radiography (Lond), 2024, 30(1): 13-20. DOI:10.1016/j.radi.2023.10.004 |
| [13] |
Cheng Z, Wen J, Huang G, et al. Applications of artificial intelligence in nuclear medicine image generation[J]. Quant Imaging Med Surg, 2021, 11(6): 2792-2822. DOI:10.21037/qims-20-1078 |
| [14] |
Mayerhoefer ME, Materka A, Langs G, et al. Introduction to radiomics[J]. J Nucl Med, 2020, 61(4): 488-495. DOI:10.2967/jnumed.118.222893 |
| [15] |
Ladefoged CN, Hansen AE, Henriksen OM, et al. AI-driven attenuation correction for brain PET/MRI: Clinical evaluation of a dementia cohort and importance of the training group size[J]. Neuroimage, 2020, 222: 117221. DOI:10.1016/j.neuroimage.2020.117221 |
| [16] |
余飞, 冯钰天, 程震, 等. 医用阿尔法核素应用策略[M]. 上海: 上海大学出版社, 2024. Yu F, Feng YT, Cheng Z, et al. Strategies and applications of targeted alpha-particle therapy[M]. Shanghai: Shanghai University Press, 2024. |
| [17] |
Sarrut D, Halty A, Badel JN, et al. Voxel-based multimodel fitting method for modeling time activity curves in SPECT images[J]. Med Phys, 2017, 44(12): 6280-6288. DOI:10.1002/mp.12586 |
| [18] |
Ritt P, Vija H, Hornegger J, et al. Absolute quantification in SPECT[J]. Eur J Nucl Med Mol Imaging, 2011, 38(Suppl 1): 69-77. DOI:10.1007/s00259-011-1770-8 |
| [19] |
Rathod N, Jutidamrongphan W, Bosbach WA, et al. Total body PET/CT: Clinical value and future aspects of quantification in static and dynamic imaging[J]. Semin Nucl Med, 2025, 55(1): 98-106. DOI:10.1053/j.semnuclmed.2024.11.004 |
| [20] |
International Commission on Radiation Units and Measurements. ICRU Report 96. Dosimetry guided radiopharmaceutical therapy[R]. Bethesda: ICRU, 2021. DOI: 10.1177/14736691211060117.
|
| [21] |
Hänscheid H, Lapa C, Buck AK, et al. Dose mapping after endoradiotherapy with 177Lu-DOTATATE/DOTATOC by a single measurement after 4 days[J]. J Nucl Med, 2018, 59(1): 75-81. DOI:10.2967/jnumed.117.193706 |
| [22] |
European Radiation Dosimetry Group. EURADOS Report 2024-01. Internal dosimetry of radiopharmaceuticals used for therapy-Towards a roadmap for patient specific dosimetry in radiopharmaceutical therapy[R]. Braunschweig: Physikalisch-Technische Bundesanstalt, 2024. DOI: 10.12768/rzq2-m816.
|
| [23] |
International Programme on Chemical Safety (IPCS). Characterization and application of physiologically based pharmacokinetic models in risk assessment[R]. Geneva: World Health Organization, 2010.
|
| [24] |
Kletting P, Muller B, Erentok B, et al. Differences in predicted and actually absorbed doses in peptide receptor radionuclide therapy[J]. Med Phys, 2012, 39(9): 5708-5717. DOI:10.1118/1.4747266 |
| [25] |
Kamp A, Andersson M, Leide-Svegborn S, et al. A revised compartmental model for biokinetics and dosimetry of 2-[18F]FDG[J]. EJNMMI Phys, 2023, 10(1): 10. DOI:10.1186/s40658-023-00528-9 |
| [26] |
International Commission on Radiological Protection. ICRP Publication 130. Occupational intakes of radionuclides: Part 1[R]. Ottawa: ICRP, 2015.
|
| [27] |
International Commission on Radiological Protection. ICRP Publication 134. Occupational intakes of radionuclides: Part 2[R]. Ottawa: ICRP, 2016.
|
| [28] |
International Commission on Radiological Protection. ICRP Publication 137. Occupational intakes of radionuclides: Part 3[R]. Ottawa: ICRP, 2017.
|
| [29] |
International Commission on Radiological Protection. ICRP Publication 141. Occupational intakes of radionuclides: Part 4[R]. Ottawa: ICRP, 2019.
|
| [30] |
International Commission on Radiological Protection. ICRP Publication 151. Occupational intakes of radionuclides: Part 5[R]. Ottawa: ICRP, 2022.
|
| [31] |
Lassmann M, Nosske D. Dosimetry of 223Ra-chloride: dose to normal organs and tissues[J]. Eur J Nucl Med Mol Imaging, 2013, 40(2): 207-212. DOI:10.1007/s00259-012-2265-y |
| [32] |
Taprogge J, Carnegie-Peake L, Murray I, et al. Adjustment of the iodine ICRP population pharmacokinetic model for the use in thyroid cancer patients after thyroidectomy[J]. J Radiol Prot, 2021, 41(4): 1034-1044. DOI:10.1088/1361-6498/ac149a |
| [33] |
Cicone F, Viertl D, Denoël T, et al. Comparison of absorbed dose extrapolation methods for mouse-to-human translation of radiolabelled macromolecules[J]. EJNMMI Res, 2022, 12(1): 21. DOI:10.1186/s13550-022-00893-z |
| [34] |
Zhuang X, Lu C. PBPK modeling and simulation in drug research and development[J]. Acta Pharm Sin B, 2016, 6(5): 430-440. DOI:10.1016/j.apsb.2016.04.004 |
| [35] |
Sheiner LB, Rosenberg B, Melmon KL. Computer-aided drug dosage[M]. New York: ACM Press, 1971.
|
| [36] |
Begum NJ, Glatting G, Wester HJ, et al. The effect of ligand amount, affinity and internalization on PSMA-targeted imaging and therapy: A simulation study using a PBPK model[J]. Sci Rep, 2019, 9: 20041. DOI:10.1038/s41598-019-56603-8 |
| [37] |
Kletting P, Bunjes D, Reske SN, et al. Improving anti-CD45 antibody radioimmunotherapy using a physiologically based pharmacokinetic model[J]. J Nucl Med, 2009, 50(2): 296-302. DOI:10.2967/jnumed.108.054189 |
| [38] |
Loeevinger R, Berman M. A schema for absorbed-dose calculations for biologically-distributed radionuclides[J]. J Nucl Med, 1968, Suppl 1: 9-14. |
| [39] |
International Commission on Radiological Protection. ICRP Publication 133. The ICRP computational framework for internal dose assessment for reference adults: specific absorbed fractions[R]. Ottawa: ICRP, 2016.
|
| [40] |
Cristy M, Eckerman K. ORNL/TM-8381. Specific Absorbed Fractions of Energy at Various Ages from Internal Photon Sources (Ⅰ-Ⅶ)[R]. Oak Ridge: Oak Ridge National Laboratory, 1987.
|
| [41] |
Menzel HG, Clement C, DeLuca P. ICRP Publication 110. Realistic reference phantoms: an ICRP/ICRU joint effort, A report of adult reference computational phantoms[R]. Ottawa: ICRP, 2009.
|
| [42] |
International Commission on Radiological Protection. ICRP Publication 143. Adult mesh-type reference computational phantoms[R]. Ottawa: ICRP, 2020.
|
| [43] |
Medical Internal Radiation Dose Committee. MIRD Pamphlet No. 11: " S, " absorbed dose per unit cumulated activity for selected radionuclides and organs[R]. New York: Society of Nuclear Medicine, 1975.
|
| [44] |
Wayson MB, Bolch WE. Individualized adjustments to reference phantom internal organ dosimetry-scaling factors given knowledge of patient external anatomy[J]. Phys Med Biol, 2018, 63(8): 085007. DOI:10.1088/1361-6560/aab72f |
| [45] |
Bouchet L, Bolch W, Blanco P, et al. MIRD Pamphlet No. 19:Absorbed fractions and radionuclide S values for six age-dependent multi-region models of the kidney[J]. J Nucl Med, 2003, 44(7): 1113-1147. |
| [46] |
Akabani G, Hawkins WG, Eckblade MB, et al. Patient-specific dosimetry using quantitative SPECT imaging and three-dimensional discrete Fourier transform convolution[J]. J Nucl Med, 1997, 38(2): 308-314. |
| [47] |
Khazaee Moghadam M, Kamali Asl A, Geramifar P, et al. Evaluating the application of tissue-specific dose kernels instead of water dose kernels in internal dosimetry: A Monte Carlo study[J]. Cancer Biother Radiopharm, 2016, 31(10): 367-379. DOI:10.1089/cbr.2016.2117 |
| [48] |
Lee MS, Kim JH, Paeng JC, et al. Whole-body voxel-based personalized dosimetry: the multiple voxel s-value approach for heterogeneous media with nonuniform activity distributions[J]. J Nucl Med, 2018, 59(7): 1133-1139. DOI:10.2967/jnumed.117.201095 |
| [49] |
Xin L, Zhuo W, Xie T. Development of a voxel S-value database for patient internal radiation dosimetry[J]. Phys Med, 2023, 106: 102519. DOI:10.1016/j.ejmp.2022.102519 |
| [50] |
Bert J, Perez-Ponce H, El Bitar Z, et al. Geant4-based Monte Carlo simulations on GPU for medical applications[J]. Phys Med Biol, 2013, 58(16): 5593-5611. DOI:10.1088/0031-9155/58/16/5593 |
| [51] |
Visvikis D, Lambin P, Beuschau Mauridsen K, et al. Application of artificial intelligence in nuclear medicine and molecular imaging: a review of current status and future perspectives for clinical translation[J]. Eur J Nucl Med Mol Imaging, 2022, 49(13): 4452-4463. DOI:10.1007/s00259-022-05891-w |
| [52] |
Lee MS, Hwang D, Kim JH, et al. Deep-dose: a voxel dose estimation method using deep convolutional neural network for personalized internal dosimetry[J]. Sci Rep, 2019, 9(1): 10308. DOI:10.1038/s41598-019-46620-y |
| [53] |
Ma Q, Chen B, Seifert R, et al. PSMA PET/CT based multimodal deep learning model for accurate prediction of pelvic lymph-node metastases in prostate cancer patients identified as candidates for extended pelvic lymph node dissection by preoperative nomograms[J]. Eur J Nucl Med Mol Imaging, 2025, 52(6): 2063-2075. DOI:10.1007/s00259-024-07065-2 |
| [54] |
Capala J, Graves SA, Scott A, et al. Dosimetry for radiopharmaceutical therapy: current practices and commercial resources[J]. J Nucl Med, 2021, 62(Suppl 3): 3-11. DOI:10.2967/jnumed.121.262749 |
| [55] |
Stabin MG, Sparks RB, Crowe E. OLINDA/EXM: the second-generation personal computer software for internal dose assessment in nuclear medicine[J]. J Nucl Med, 2005, 46(6): 1023-1027. |
| [56] |
International Commission on Radiation Units and Measurements. ICRU Report 98. Stochastic nature of radiation interactions: Microdosimetry[R]. Bethesda: ICRU, 2023.
|
| [57] |
Cicone F, Sj green Gleisner K, Sarnelli A, et al. The contest between internal and external-beam dosimetry: The Zeno's paradox of Achilles and the tortoise[J]. Phys Med, 2024, 117: 103188. DOI:10.1016/j.ejmp.2023.103188 |
| [58] |
Goddu SM, Howell RW, Bouchet LG, et al. MIRD cellular S values: self-absorbed dose per unit cumulated activity for selected radionuclides and monoenergetic electron and alpha particle emitters incorporated into different cell compartments[M]. New York: Society of Nuclear Medicine, 1997.
|
| [59] |
Vaziri B, Wu H, Dhawan AP, et al. MIRD pamphlet No. 25:MIRDcell V2.0 software tool for dosimetric analysis of biologic response of multicellular populations[J]. J Nucl Med, 2014, 55(9): 1557-1564. DOI:10.2967/jnumed.113.131037 |
| [60] |
Kyriakou I, Sakata D, Tran HN, et al. Review of the Geant4-DNA simulation toolkit for radiobiological applications at the cellular and DNA level[J]. Cancers (Basel), 2021, 14(1): 35. DOI:10.3390/cancers14010035 |
| [61] |
Barendsen GW. Dose fractionation, dose rate and iso-effect relationships for normal tissue responses[J]. Int J Radiat Oncol Biol Phys, 1982, 8(11): 1981-1997. DOI:10.1016/0360-3016(82)90459-x |
| [62] |
Lea DE, Catcheside DG. The mechanism of the induction by radiation of chromosome aberrations in Tradescantia[J]. J Genet, 1942, 44(1): 216-245. DOI:10.1007/BF02982830 |
| [63] |
Niemierko A. Reporting and analyzing dose distributions: a concept of equivalent uniform dose[J]. Med Phys, 1997, 24(1): 103-110. DOI:10.1118/1.598063 |
| [64] |
O'Donoghue JA. Implications of nonuniform tumor doses for radioimmunotherapy[J]. J Nucl Med, 1999, 40(8): 1337-1341. |
 2025, Vol. 45
2025, Vol. 45