2. 中山大学-国科离子放射治疗前沿技术联合实验室, 广州 510060
2. United Laboratory of Frontier Radiotherapy Technology of Sun Yat-sen University & Chinese Academy of Sciences Ion Medical Technology Co., Ltd, Guangzhou 510060, China
相较于光子放疗,碳离子因其更佳的相对生物效能(relative biological effectiveness,RBE)和倒转的深度剂量分布引起研究者的关注,成为放射治疗领域的热点之一[1]。
研究表明,RBE值受到物理、化学和生物因素的共同影响,如射线品质、细胞或组织器官放射敏感性、生物效应终点、含氧水平等[2-4]。RBE实验测量面临诸多困难,基于生物物理模型的计算方法逐渐发展成为RBE值评估的主要手段。作为国际上最大的重离子医学研究中心,日本国立放射医学研究所(National Institute of Radiological Science,NIRS)发展了用于生物RBE计算的微剂量动力学模型(microdosimetric kinetic model,MKM)。该模型理论框架由Hawkins[5-7]提出,经Kase等[8-9]和Inaniwa等[10]修正后用于混合辐射场中的临床RBE预测。
尽管MKM能够较好地预测带电粒子照射下的离体细胞存活效应,但仍存在一定的局限。多项细胞实验研究结果表明,重离子照射下细胞存活分数拟合参数α和β表现出一定的细胞放射敏感性依赖[3, 11]。大阪重离子放疗中心Wakisaka等[12]使用碳离子对前列腺癌细胞进行照射,剂量重建结果表明,肿瘤内存在由细胞放射敏感性不同所导致的响应差异。近年来研究人员对电离辐射诱导细胞双链断裂(double strand break, DSB)损伤开展了相关实验测量与模拟计算,特别是对于重离子的研究日益增多[13]。Chen等[14]考虑初级辐射损伤产额与传能线密度(linear energy transfer, LET)的关系,建立了修正微剂量动力学模型(modified microdosimetric kinetic model, MMKM)。现有文献中的生物RBE模型通常仅考虑了不同LET值或粒子类型对结果的影响,本研究在上述文献的基础上,进一步开展细胞系辐射敏感性对微剂量动力学模型的影响研究。
材料与方法1. 微剂量动力学模型(MKM):在MKM理论推导中,每个细胞核被划分为多个更微小的亚细胞核体积,称为domain,认为domain内产生的致死事件数与其内沉积的比能(z)呈线性平方关系。进一步地,细胞群体中平均存活分数可表示为:
| $ S=\exp \left(-L_n\right) $ | (1) |
式中,Ln为细胞群体中的平均损伤数量:
| $ L_n=\left(\alpha_0+\beta z_{\text {ld }}^*\right) D+\beta D^2 $ | (2) |
式中,α0和β为模型参数,可通过细胞存活曲线拟合获得;D为细胞受到剂量,Gy;z1d*为单次能量沉积事件在domain内沉积的饱和校正剂量平均比能,表述如下:
| $ z_{1 \mathrm{~d}}^*=\frac{\int_0^{\infty} z_{\text {sat }} z f_1(z) d z}{\int_0^{\infty} z f_1(z) d z} $ | (3) |
式中,f1(z)为在单次能量沉积事件中domain内比能的概率密度分布;zsat为饱和校正比能:
| $ z_{\text {sat }}=\frac{z_0^2}{z}\left(1-\exp \left(-\frac{z^2}{z_0^2}\right)\right) $ | (4) |
式中,饱和参数z0由domain半径rd、细胞核半径Rn和β参数给出:
| $ z_0=\frac{\left(R_{\mathrm{n}} / r_{\mathrm{d}}\right)^2}{\sqrt{\beta\left(1+\left(R_{\mathrm{n}} / r_{\mathrm{d}}\right)^2\right)}} $ | (5) |
2. Kiefer-Chatterjee(K-C)模型:K-C模型被用来确定带电粒子在距离径迹中心r 位置处微观径向物理剂量的变化[15-16]。带电粒子径向上径迹结构包括两部分:在r≤Rcore的径迹核心区域,物理剂量恒定为Dcore;在径迹中心区域以外的半影区域,物理剂量Dpenumbra随半径r的增加以1/r2的比例迅速降低。
| $ D_{\text {penumbra }}=1.25 \times 10^{-4}\left(\frac{Z_{\text {eff }}}{\beta_{\mathrm{v}}}\right){ }^2 r^{-2}=K_{\mathrm{p}} r^{-2} r>R_{\text {core }} $ | (6) |
| $ D_{\text {core }}=\frac{1}{\pi R_{\mathrm{c}}^2}\left(L E T-2 \pi K_{\mathrm{p}} \operatorname{In}\left(\frac{R_{\mathrm{p}}}{R_{\mathrm{c}}}\right)\right) r \leqslant R_{\text {core }} $ | (7) |
| $ R_{\text {core }}=0.0116 \beta_v $ | (8) |
| $ R_{\text {penumbra }}=0.0616\left(\frac{E}{A}\right)^{1.7} $ | (9) |
式中,E和A分别为带电粒子的动能(MeV)和质量数;Zeff为带电粒子的有效电荷;βv为带电粒子速度相对于光速的比值:
| $ Z_{\text {eff }}=Z\left[1-\exp \left(-125 \cdot \beta_v \cdot Z^{-\frac{2}{3}}\right)\right] $ | (10) |
| $ \beta_v=\sqrt{1-\frac{1}{\left(1+\frac{E}{m c^2}\right)^2}} $ | (11) |
式中,mc2为带电粒子的静止能量,带电粒子的动能LET值数据来源于最新的libdEdx数据库(https://aptg.github.io/web/Calculator)。
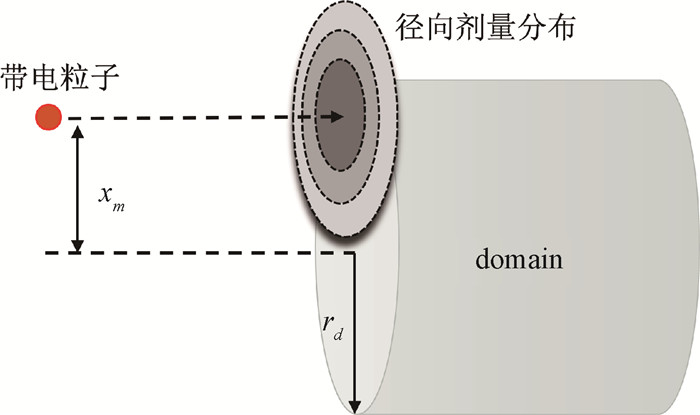
3. z1d*的计算:α0、rd和Rn参数的确定是RBE与D10计算的先决条件,本研究采用Chen等[14]拟合得到的MMKM参数值(α0=0.15 Gy-1,rd=0.38 μm,Rn=5.0 μm)。基于带电粒子在液态水中的微观径向物理剂量分布解析模型,计算单能碳离子射线的z1d*值,见图 1。
|
注:domain. 细胞核内假想的更微小的亚细胞核结构 图 1 带电粒子入射domain示意图 Figure 1 Schematic diagram showing the incidence of a charged particle into a domain |
假设domain是半径为rd的圆柱体敏感域,带电粒子沿敏感域轴线方向入射,忽略带电粒子穿过domain过程中能量的变化。径迹结构模型的中心轴到敏感域中心轴的距离,称为碰撞参数(Xm)。利用K-C径迹剂量分布模型,计算径迹中心与domain中心不同距离x时的domain内的比能z(x) 及饱和校正的比能zsat(x),进而根据公式(12)获得饱和校正的剂量平均比能z1d*:
| $ \begin{gathered} z_{\mathrm{1d}}^*=\frac{\int_0^{x_{\mathrm{m}}} z_{\text {sat }}(x) z(x) \cdot 2 \pi x \mathrm{~d} x / \int_0^{x_{\mathrm{m}}} 2 \pi x \mathrm{~d} x}{\int_0^{x_{\mathrm{m}}} z(x) \cdot 2 \pi x \mathrm{~d} x / \int_0^{x_{\mathrm{m}}} 2 \pi x \mathrm{~d} x}= \\ \frac{\int_0^{x_m} z_{\text {sat }}(x) z(x) \cdot 2 \pi x \mathrm{~d} x}{\int_0^{x_{\mathrm{m}}} z(x) \cdot 2 \pi x \mathrm{~d} x} \end{gathered} $ | (12) |
所涉及到的二重积分均通过MATLAB R2022b软件里的符号积分函数实现。
4. f(LET)修正曲线:在MKM理论推导中,假设电离辐射在每个domain内可产生两类初级辐射损伤,两种损伤的数目均与domain内沉积比能成正比,且占比较大的第二类初级辐射损伤可能是DNA双链断裂。MKM默认细胞存活分数仅取决于domain内沉积比能,与照射射线的辐射品质无关,这与哺乳动物的细胞实验结果不符,即DSB产额是随射线LET而变化的。针对上述问题,Chen等[14]引入考虑初级辐射损伤产额与射线LET值的关系,通过对RBE-DSB实验测量数据的拟合得到RBEDSB-LET关系曲线,即f(LET),建立MMKM:
| $ \ln S(D)=-\alpha D-\beta D^2 $ | (13) |
| $ \begin{gathered} \ln S(D)=-\left(f(\text { LET }) A+z_{1 \mathrm{~d}}^* f^2(\text { LET }) B\right) D- \\ f^2(\text { LET }) B D^2 \end{gathered} $ | (14) |
MMKM可以较好地应用于日本NIRS临床中使用的中等辐射敏感性的人体唾液腺细胞(HSG)细胞,但在应用于其他一些细胞类型时仍有局限。因此,本研究计划基于实验数据探索建立不同辐射敏感性细胞系条件下的模型变化研究。使用多项式最小二乘法拟合获得f(LET)修正曲线。
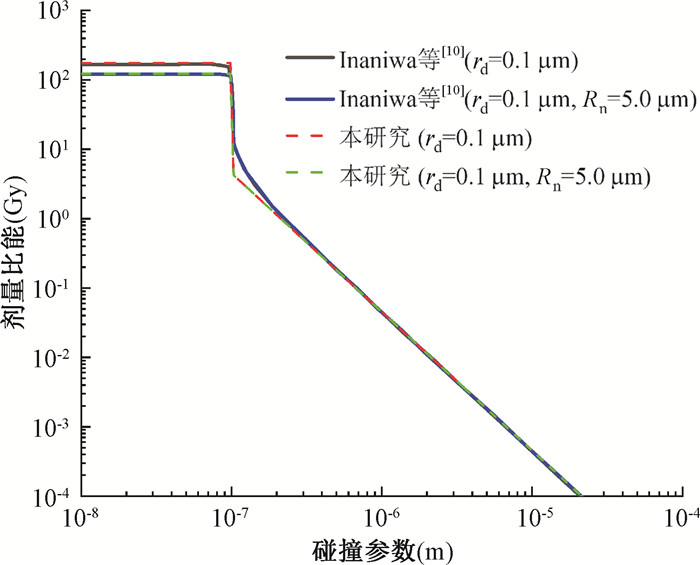
结果1. K-C模型:图 2为碳离子在domain半径为0.1 μm以及细胞核半径为5.0 μm条件下的比能分布,横坐标为碰撞参数,最大取值为敏感域半径rd与粒子径迹结构半影区域半径RP之和。带电粒子能量为50 MeV/u碳离子,查表可得对应LET为45.3 keV/μm。图中实线代表文献中的计算结果[10],虚线为本研究的复现结果。可以看出,两者在幅度及趋势上基本重合,验证了本算法的合理性。
|
图 2 50 MeV/u碳离子在不同尺寸domain内沉积比能随碰撞参数的分布 Figure 2 Specific energy distribution within domains of varying sizes varying with the collision parameter for 50 MeV/u carbon ions |
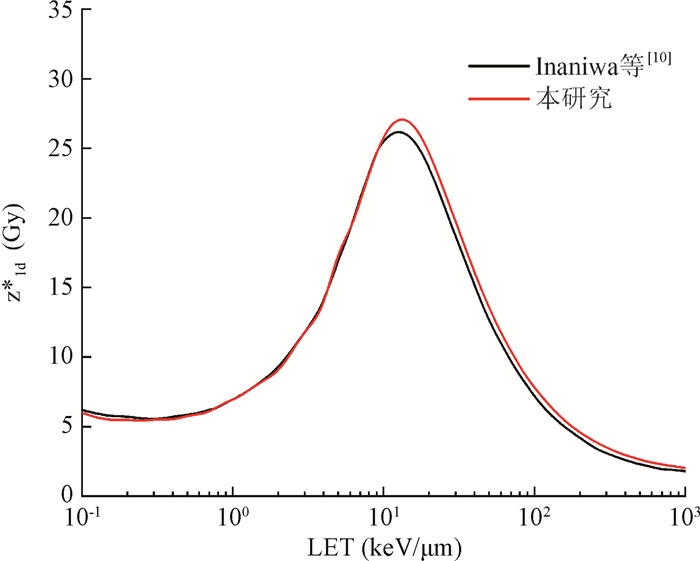
2. z1d*的计算:图 3为根据公式(4)计算所得碳离子饱和校正比能随粒子动能的变化关系。图中黑色实线来自Inaniwa等[10]文献中的计算结果,红色实线代表本工作计算结果,计算中所使用的domain和细胞核半径参数与文献[10] 一致,rd=0.32μm,Rn=3.9μm。相较于其他文献结果[17],本工作通过采用合理的积分步长在低能区与文献结果一致性更好,在碳离子能量大于10 MeV/u时计算结果略高于文献结果,这可能是数据库选择差异所导致。总体而言,本工作可以较好地复现文献中的计算结果。
|
注:z1d*.饱和校正的剂量平均比能;LET.传能线密度 图 3 单能碳离子饱和校正平均比能随动能变化关系 Figure 3 z1d* for monoenergetic carbon ions varying with kinetic energy |
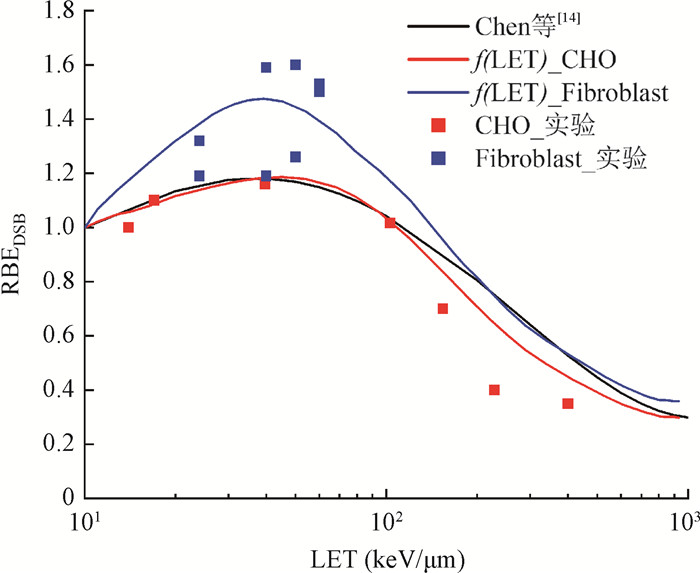
3. f(LET)修正曲线:图 4为两种细胞系实验RBEDSB随碳离子LET值关系及拟合所得f(LET) 修正曲线[18-19]。可以看出,相较于文献中不区分细胞系的拟合曲线,本研究获得的拟合结果在整体上与实验数据一致性更好。
|
注:RBEDSB.通过DSB产额比值定义得到的RBE值;LET. 线传能密度;CHO.中国仓鼠卵巢细胞;Fibroblast. 成纤维细胞 图 4 两种细胞系实验RBEDSB随碳离子LET值关系及修正f(LET) Figure 4 RBEDSB values of CHO and Fibroblast cell lines varying with the LET value of carbon ions and corrected f(LET) |
4. D10随LET的分布:图 5为两种细胞10%存活分数对应的物理剂量实验值(D10)随碳离子LET关系变化,蓝色数据点代表在碳离子照射下实验测量得到的CHO细胞10%存活分数对应物理剂量分布[20],红色数据点代表在碳离子照射下Fibroblast细胞10%存活分数对应物理剂量[21-23]。两种颜色实线分别对应本研究计算得到的碳离子在不同LET条件下两种细胞系的D10变化曲线。可以看出,在LET < 100 keV/μm时,本研究给出的计算结果与MKM相比,可以更为准确地拟合Fibroblast细胞系实验测量结果,本研究计算D10(蓝色实线)与文献中实验测量结果的均方误差为0.35,MKM为0.55;而在LET>100 keV/μm时,本研究则可以较好地预测CHO细胞系的实验测量结果,本研究计算D10(红色实线)与文献中实验测量结果的均方误差为0.04,MKM为0.71,提示MKM存在一定的低估。
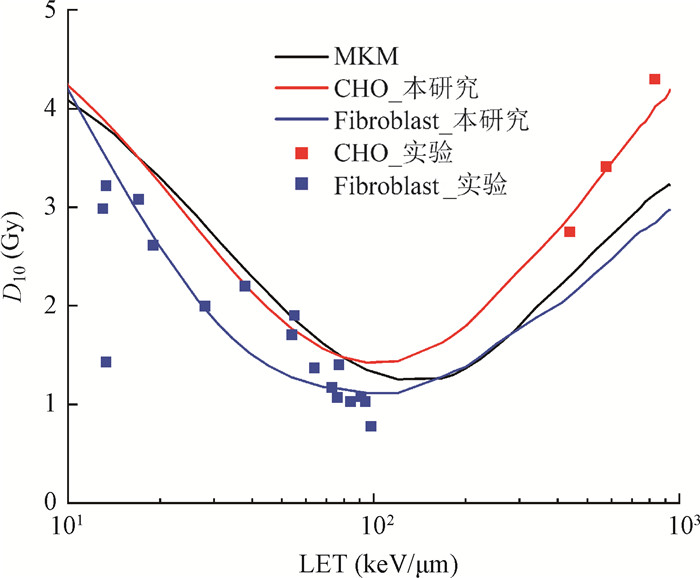
|
注:D10.细胞10%存活分数对应受到的物理剂量;LET.传能线密度;MKM.微剂量动力学模型的预测结果;CHO.中国仓鼠卵巢细胞;Fibroblast.成纤维细胞 图 5 两种细胞系实验D10随碳离子LET关系 Figure 5 D10 values of CHO and Fibroblast cell lines varying with the LET values of carbon ions |
5. α随LET的分布:图 6为碳离子不同LET下计算α值与实验结果的比较。可以看出,本研究得到的两种细胞系条件下α分布整体与MKM趋势一致。在LET < 100 keV/μm时,本研究中CHO细胞系的α计算结果与MKM预测结果大致重合,MKM对于LET < 40 keV/μm时HSG细胞实验结果均存在明显的高估,在10~1 000 keV/μm范围内,本研究可以更好地预测CHO细胞实验测量结果;此外,绝大部分情况下本研究中Fibroblast细胞系的α计算结果均高于CHO细胞系和MKM的结果,呈现与辐射敏感性正相关的趋势,且在LET>100 keV/μm时,与HSG实验数据一致性更好。
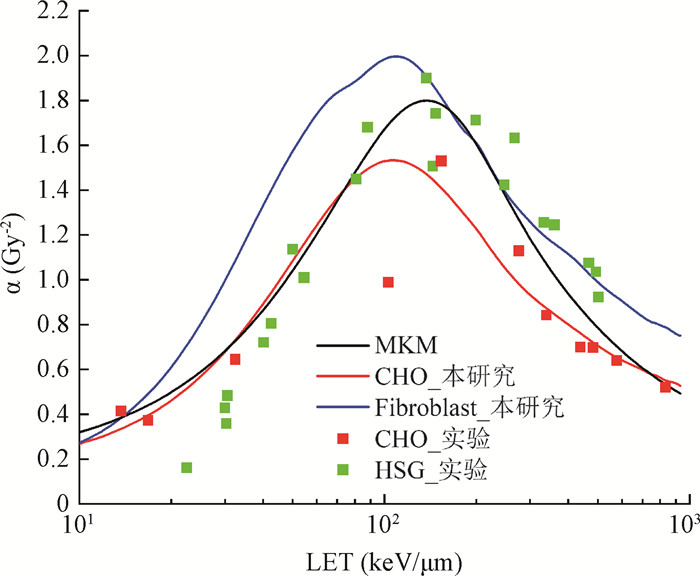
|
注:LET.传能线密度;MKM.微剂量动力学模型的预测结果;CHO.中国仓鼠卵巢细胞;Fibroblast.成纤维细胞 图 6 碳离子不同LET下计算α值与实验结果比较 Figure 6 Comparison of calculated and experimental α values of carbon ions under varying LET values |
6. β随LET的分布:图 7为碳离子不同LET下计算β值与实验结果的比较。显示碳离子照射条件下实验测量的剂量二次项系数β在20~100 keV/μm范围总体上呈下降趋势,在>100 keV/μm后迅速趋向于0,需要注意的是,LET在20~60 keV/μm范围实验数据的离散度较大,可能是由于测量的不确定度和测量方法不同引起。本研究中两种细胞系计算β值先随LET缓慢上升,CHO细胞系和Fibroblast细胞系分别在50和40 keV/μm附近达到峰值后转而下降,并在高LET时趋于0。对比图 4可知,经过f(LET)修正的计算β值与二类初级辐射损伤产额的平方成正比,即β随LET的变化曲线与f 2(LET)曲线成正比。
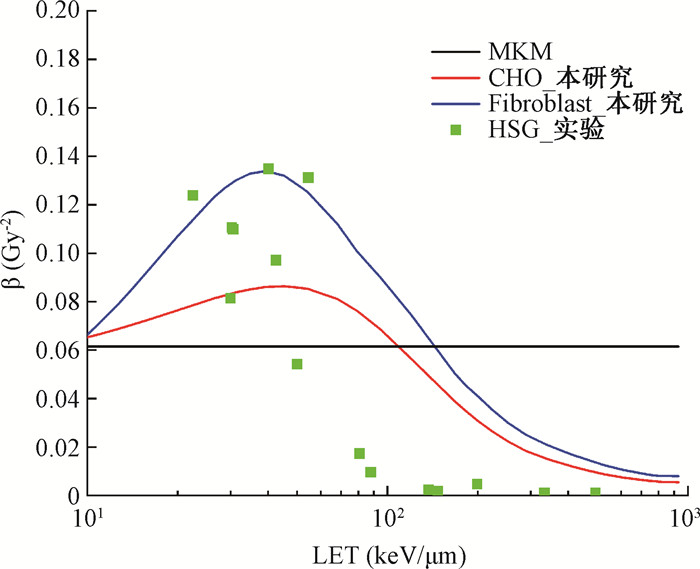
|
注:LET.传能线密度;MKM.微剂量动力学模型的预测结果;CHO.中国仓鼠卵巢细胞;Fibroblast.成纤维细胞 图 7 碳离子不同LET下计算β值与实验结果比较 Figure 7 Comparison of calculated and experimental β values of carbon ions under varying LET values |
讨论
RBE是碳离子临床放射治疗照射方案制定的重要依据,定义为产生相同辐射生物学效应所需的光子与带电粒子物理剂量的比值,直接影响肿瘤控制率与正常组织并发症概率,是临床应用的难点之一。NIRS在辐射损伤、修复动力学和离体细胞实验数据的基础上发展了基于线性平方模型的RBE计算方法MKM,并将其推广应用于重离子的临床治疗中,成为认可度较高的RBE计算模型之一。在其理论推导中,MKM将射线辐射品质不同所导致辐射生物效应的差异仅归因于亚细胞核体积中能量沉积的不均匀性,认为在亚细胞核内不同射线以及不同细胞系间的剂量-响应特性没有区别,辐射损伤致DNA的DSB产额取决于剂量大小。这与DSB产额可能受到射线品质与细胞系辐射敏感性影响[2-3, 19, 24]的实验结果不符。NIRS目前在临床放疗中使用的RBE模型是建立在中等辐射敏感性的离体HSG细胞实验数据基础上,尚未考虑不同细胞辐射敏感性的影响,即默认患者体内实体肿瘤靶区内癌细胞均匀分布且具有等同的放射敏感性,在治疗计划系统给定的剂量分布下也具有相同的细胞存活曲线[4, 25]。实际上,体内肿瘤区域不同位置处细胞的放射敏感性差异是存在的,受到细胞固有放射敏感性、增殖周期、氧浓度和对损伤的修复能力等因素的共同影响[26]。总体而言,目前未考虑细胞放射敏感性差异的RBE模型可能会造成局部肿瘤区域生物效应的降低,最终导致临床治疗失败[27]。因此,本研究在MKM基础上,通过分析两种不同辐射敏感性细胞系实验DSB产额的RBE值随碳离子射线LET的变化规律,引入f(LET)修正MKM中二类初级辐射损伤产额,从而建立了考虑细胞放射敏感性的RBE模型。进一步地,使用K-C模型计算单能碳离子的饱和校正比能,给出单能碳离子射线下两种细胞系的α和β值以及不同LET下的D10。相较于MKM,本研究中经过细胞系f(LET)修正后的D10分布可以与两种细胞系实验测量结果更好地吻合。由于现有文献中缺乏两种细胞系下实验测量的β值,本研究中的数据仅为碳离子照射条件下的实验数据,并未区分细胞系类型。相较于MKM模型,通过引入特定细胞系辐射敏感性的f(LET) 修正,本研究中的计算α结果可以更好地与实验数据吻合,且在整体趋势上与MKM预测结果一致,验证了本方法的有效性。
无论是MKM或LEM,模型中的基本参数(α0、rd和Rn等)均来源于离体细胞实验数据的拟合结果。研究表明,相较于其他参数,rd的变化将造成最显著的生物剂量分布差异,rd增加25%将导致拓展布拉格峰中心区域14%的生物剂量下降[28]。由于目前相关细胞系实验数据的缺乏,本研究中所用参数依然采用文献中推荐计算结果,考虑到特定细胞系f(LET) 修正曲线的引入,HSG、CHO和Fibroblast细胞系对应不同rd参数的使用所导致差异有可能被进一步缩小,未来将针对此问题开展进一步研究。
本研究在MKM和MMKM基础上进行了理论修正,考虑了细胞辐射敏感性的影响因素,有望使临床碳离子治疗中具有不同细胞放射敏感性的肿瘤放疗获益,为MKM的进一步发展和RBE值的精确计算提供参考。
利益冲突 无
作者贡献声明 宋鸿鹄负责数据整理与分析、论文撰写与修改;朴尊、黄国敏负责数据核对,论文修改与撰写;石健参与论文修改;陈明、黄晓延负责选题设计、审阅论文
| [1] |
Malouff TD, Mahajan A, Krishnan S, et al. Carbon ion therapy: a modern review of an emerging technology[J]. Front Oncol, 2020, 10: 82. DOI:10.3389/fonc.2020.00082 |
| [2] |
Stewart RD, Yu VK, Georgakilas AG, et al. Effects of radiation quality and oxygen on clustered DNA lesions and cell death[J]. Radiat Res, 2011, 176(5): 587-602. DOI:10.1667/rr2663.1 |
| [3] |
Friedrich T, Scholz U, Elsässer T, et al. Systematic analysis of RBE and related quantities using a database of cell survival experiments with ion beam irradiation[J]. J Radiat Res, 2013, 54(3): 494-514. DOI:10.1093/jrr/rrs114 |
| [4] |
Furusawa Y, Fukutsu K, Aoki M, et al. Inactivation of aerobic and hypoxic cells from three different cell lines by accelerated 3He-, 12C-and 20Ne-ion beams[J]. Radiat Res, 2000, 154(5): 485-496. DOI:10.1667/0033-7587(2000)154[0485:ioaahc]2.0.co;2 |
| [5] |
Hawkins RB. A statistical theory of cell killing by radiation of varying linear energy transfer[J]. Radiat Res, 1994, 140(3): 366-374. |
| [6] |
Hawkins RB. A microdosimetric-kinetic theory of the dependence of the RBE for cell death on LET[J]. Med Phys, 1998, 25(7 Pt 1): 1157-1170. DOI:10.1118/1.598307 |
| [7] |
Hawkins RB. A microdosimetric-kinetic model for the effect of non-Poisson distribution of lethal lesions on the variation of RBE with LET[J]. Radiat Res, 2003, 160(1): 61-69. DOI:10.1667/rr3010 |
| [8] |
Kase Y, Kanai T, Matsufuji N, et al. Biophysical calculation of cell survival probabilities using amorphous track structure models for heavy-ion irradiation[J]. Phys Med Biol, 2008, 53(1): 37-59. DOI:10.1088/0031-9155/53/1/003 |
| [9] |
Kase Y, Kanai T, Matsumoto Y, et al. Microdosimetric measurements and estimation of human cell survival for heavy-ion beams[J]. Radiat Res, 2006, 166(4): 629-638. DOI:10.1667/RR0536.1 |
| [10] |
Inaniwa T, Furukawa T, Kase Y, et al. Treatment planning for a scanned carbon beam with a modified microdosimetric kinetic model[J]. Phys Med Biol, 2010, 55(22): 6721-6737. DOI:10.1088/0031-9155/55/22/008 |
| [11] |
Suárez-García D, Cortés-Giraldo MA, Bertolet A. A systematic analysis of the particle irradiation data ensemble in the key of the microdosimetric kinetic model: Should clonogenic data be used for clinical relative biological effectiveness?[J]. Radiother Oncol, 2023, 185: 109730. DOI:10.1016/j.radonc.2023.109730 |
| [12] |
Wakisaka Y, Minami K, Okada N, et al. Treatment planning of carbon ion radiotherapy for prostate cancer based on cellular experiments with PC3 human prostate cancer cells[J]. Phys Med, 2023, 107: 102537. DOI:10.1016/j.ejmp.2023.102537 |
| [13] |
Frese MC, Yu VK, Stewart RD, et al. A mechanism-based approach to predict the relative biological effectiveness of protons and carbon ions in radiation therapy[J]. Int J Radiat Oncol Biol Phys, 2012, 83(1): 442-450. DOI:10.1016/j.ijrobp.2011.06.1983 |
| [14] |
Chen Y, Li J, Li C, et al. A modified microdosimetric kinetic model for relative biological effectiveness calculation[J]. Phys Med Biol, 2017, 63(1): 015008. DOI:10.1088/1361-6560/aa9a68 |
| [15] |
Chatterjee A, Schaefer HJ. Microdosimetric structure of heavy ion tracks in tissue[J]. Radiat Environ Biophys, 1976, 13(3): 215-227. DOI:10.1007/BF01330766 |
| [16] |
Kiefer J, Straaten H. A model of ion track structure based on classical collision dynamics[J]. Phys Med Biol, 1986, 31(11): 1201-1209. DOI:10.1088/0031-9155/31/11/002 |
| [17] |
Magro G, Dahle TJ, Molinelli S, et al. The FLUKA Monte Carlo code coupled with the NIRS approach for clinical dose calculations in carbon ion therapy[J]. Phys Med Biol, 2017, 62(9): 3814-3827. DOI:10.1088/1361-6560/aa642b |
| [18] |
Heilmann J, Taucher-Scholz G, Kraft G. Induction of DNA double-strand breaks in CHO-K1 cells by carbon ions[J]. Int J Radiat Biol, 1995, 68(2): 153-162. DOI:10.1080/09553009514551051 |
| [19] |
Höglund E, Blomquist E, Carlsson J, et al. DNA damage induced by radiation of different linear energy transfer: initial fragmentation[J]. Int J Radiat Biol, 2000, 76(4): 539-547. DOI:10.1080/095530000138556 |
| [20] |
Czub J, Bana D, Błaszczyk A, et al. Biological effectiveness of 12C and 20Ne ions with very high LET[J]. Int J Radiat Biol, 2008, 84(10): 821-829. DOI:10.1080/09553000802389652 |
| [21] |
Suzuki M, Kase Y, Yamaguchi H, et al. Relative biological effectiveness for cell-killing effect on various human cell lines irradiated with heavy-ion medical accelerator in Chiba (HIMAC) carbon-ion beams[J]. Int J Radiat Oncol Biol Phys, 2000, 48(1): 241-250. DOI:10.1016/s0360-3016(00)00568-x |
| [22] |
Tsuruoka C, Suzuki M, Kanai T, et al. LET and ion species dependence for cell killing in normal human skin fibroblasts[J]. Radiat Res, 2005, 163(5): 494-500. DOI:10.1667/rr3360 |
| [23] |
Kitajima S, Nakamura H, Adachi M, et al. AT cells show dissimilar hypersensitivity to heavy-ion and X-rays irradiation[J]. J Radiat Res, 2010, 51(3): 251-255. DOI:10.1269/jrr.09069 |
| [24] |
Flint DB, Bright SJ, McFadden CH, et al. Cell lines of the same anatomic site and histologic type show large variability in intrinsic radiosensitivity and relative biological effectiveness to protons and carbon ions[J]. Med Phys, 2021, 48(6): 3243-3261. DOI:10.1002/mp.14878 |
| [25] |
Inaniwa T, Kanematsu N, Matsufuji N, et al. Reformulation of a clinical-dose system for carbon-ion radiotherapy treatment planning at the national institute of radiological sciences, Japan[J]. Phys Med Biol, 2015, 60(8): 3271-3286. DOI:10.1088/0031-9155/60/8/3271 |
| [26] |
Suit H, Skates S, Taghian A, et al. Clinical implications of heterogeneity of tumor response to radiation therapy[J]. Radiother Oncol, 1992, 25(4): 251-260. DOI:10.1016/0167-8140(92)90244-o |
| [27] |
Inaniwa T, Kanematsu N, Koto M. Biological dose optimization incorporating intra-tumoural cellular radiosensitivity heterogeneity in ion-beam therapy treatment planning[J]. Phys Med Biol, 2024, 69(11). DOI:10.1088/1361-6560/ad4085 |
| [28] |
Dahle TJ, Magro G, Ytre-Hauge KS, et al. Sensitivity study of the microdosimetric kinetic model parameters for carbon ion radiotherapy[J]. Phys Med Biol, 2018, 63(22): 225016. DOI:10.1088/1361-6560/aae8b4 |
 2025, Vol. 45
2025, Vol. 45


