2. 中山大学肿瘤防治中心, 华南肿瘤学国家重点实验室, 广州 510060
2. State Key Laboratory of Oncology in South China, Sun Yat-sen University Cancer Center, Guangzhou 510060, China
肺癌预后引导放疗计划设计方法通过将预后解析模型引入计划逆向优化过程中,量化表示潜在的预期临床控制与风险,为客观平衡肿瘤与正常组织器官的受照剂量提供了理论手段[1],有望进一步提高肺癌患者的临床获益[2-3]。然而,预后模型的纳入为放疗计划的逆向优化求解带来了挑战:预后模型的高度非凸性令优化目标出现多极值特性,采用物理剂量最优策略下的常规梯度算法求解无法提供全局最优计划,不利于患者临床治疗[4-5]。在满足临床有限时间窗口下,高效寻找全局最优解,是预后引导计划自动优化首当其冲的问题[6]。对此,Modiri等[7]提出采用粒子群算法(particle swarm optimization, PSO)求解预后计划的非凸问题,但由于PSO在高维空间中容易出现早熟收敛,其可行性目前仅能在三维适形放疗中得以验证[8]。随机对比交互粒子群算法(RCIPSO)作为一种高效大规模群体智能算法,通过随机对比交互策略,使粒子群在高维空间中也能充分探索整个解空间实现全局优化,为调强放疗(IMRT)的预后计划优化提供了新的理论方法[9]。但和其他群体智能算法一样,RCIPSO也基于随机搜索,这使得该算法需通过百万次的函数评估探索解空间以保证算法的稳定收敛,完成单次计划优化需数小时,无法满足临床时效性[10]。综上,为快速、准确地求解IMRT预后引导计划优化问题,本研究对RCIPSO进行改进,通过引入最速下降方向,让粒子直接学习局部邻域景观,借此降低算法局部搜索所需的函数评估次数,旨在不损失算法全局优化精度的同时,进一步提升算法的收敛速度。
资料与方法1.实验流程:本研究首先构建肺癌预后引导的IMRT计划优化模型,该模型既需兼顾临床主流剂量统计约束标准,又需考虑患者预期预后并令其最佳,同时还需满足实际的机械可执行性。其次,提出一种基于梯度增强的随机对比交互粒子群算法(gradient-enhanced random contrastive interaction particle swarm optimization, GradRCIPSO)对上述大规模非凸模型进行快速全局最优寻解。最后,通过回顾性收集多例临床肺癌IMRT计划并重新优化,开展结果分析验证方法的可行性。
2.病例资料:回顾性收集10例既往接受过IMRT的非小细胞肺癌(NSCLC)患者的计划数据,计划涉及的感兴趣区域有靶区、肺、心脏、食管和脊髓。其中,靶体积范围为41~725 cm3,处方剂量为42~64 Gy。所有病例均行5野共面照射,其靶区勾画、射野设计及计划设计均由资深物理师在临床规范的引导下完成,并通过6 MV的光子直线加速器执行。
3.肺癌预后引导IMRT的计划优化模型:本研究建立的数学模型为带约束的最小化目标函数式,如图 1所示。其中,目标函数F(x)包含辐射致各OAR放疗毒性发生/肿瘤控制失败风险概率项(①)以及射野强度分布平滑项(②)两部分,用于引导计划自动趋向放疗总风险(各放疗毒性风险及肿瘤控制失败风险的累积概率)最低,同时满足实际机械平滑要求;约束(c3)用于限制靶区剂量均匀性;约束(c4)~(c5)和(c6)~(c7) 分别用于限制低剂量和高剂量区域。

|
图 1 基于预后引导的计划优化模型 Figure 1 Prognosis-guided IMRT plan optimization model |
具体地,肺癌放疗预后风险事件包括放疗后肺癌2年局部控制失败(local-regional failure, LRF2y)[11]、≥3级心脏不良事件(cardiac events, CE3+)[12]、≥3级放射性肺炎(radiation-induced lung toxicity, RILT3+)[13]和≥2级急性放射性食管炎(acute radiation-induced esophagitis, ARIE2+)[14]。平滑项fsmooth为射野通量矩阵拉普拉斯离散的平方和[15];x为照射野通量强度,是优化变量;D为剂量沉积矩阵,由放疗开源软件包CERR[16]计算得出;θRs, m是器官s在接受d剂量照射后诱发风险事件m的概率PRs, m所对应的权重;γ是平滑项对应权重。剂量约束项采用肺癌美国国立综合癌症网络(NCCN)临床实践指南[17]以及临床实践经验共同给出。
4.基于梯度增强的随机对比交互粒子群(GradRCIPSO)寻优策略:所提算法整体框架如图 2所示。算法初始阶段,首先在解空间内随机生成N个不同的通量向量Xi0(i=1, 2, …, N),即初始化粒子群的位置,同时设置每个粒子的初始速度Vi0为0。其次,代入患者的基础数据与射束信息,进行目标函数建模,目标函数值即为优化过程中的适应度f(X)。接下来,计算初始粒子群的适应度并进行比较,记录适应度值最小的粒子为初始全局最优通量G。随后,开始迭代更新,每个粒子Xit通过学习整个解空间中优质通量分布所处的位置和局部梯度信息所代表的适应度下降方向得到新的粒子位置Xit+1。待所有粒子更新完毕,评估这些粒子在新位置的适应度值,并更新全局最优通量G,进入下一次迭代,直到满足预定义的终止条件算法结束。最后将当前最优解G作为最终求解得到的通量分布输出。
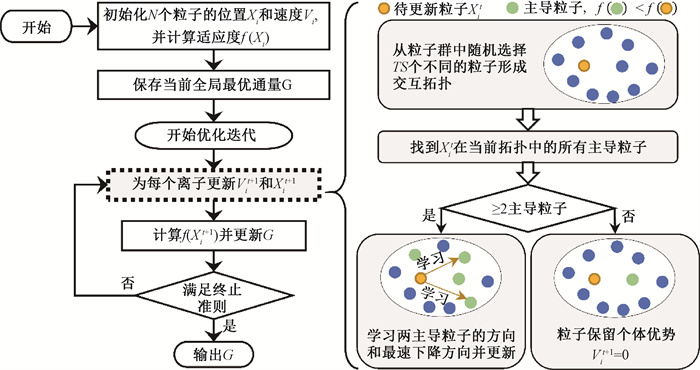
|
图 2 基于梯度增强的粒子群算法优化流程图 Figure 2 Flow chart of gradient-enhanced particle swarm optimization algorithm |
具体地,粒子Xi在t+1时刻的搜索方向由粒子惯性Vit、交互信息Interactit+1和梯度增强信息Gradit+1共同决定,如式(1)和(2)所示。式中,c1、c2和c3是衡量三个组分的权重;r为[0, 1]内均匀采样的随机向量。
| $ V_i^{t+1}=c_1 r V_i^t+c_2 \text { Interact }_i^{t+1}+c_3 \text { Grad }_i^{t+1} $ | (1) |
| $ X_i^{t+1}=X_i^t+V_i^{t+1} $ | (2) |
在式(1)中,第一项粒子惯性由粒子t时刻的速度Vit表征,有利于帮助粒子探索较大的通量空间。第二项交互信息Interactit+1则使粒子可以在全局范围内找到最优通量所处的区域。如图 2右侧所示,当粒子Xi更新时,将学习交互拓扑中适应度差异最大的两个主导粒子Xbest和Xworst的搜索方向:
| $ \text { Interact }_i^{t+1}=r_1\left(X_{\text {best }}-X_i^t\right)+\varphi r_2\left(X_{\text {worst }}-X_i^t\right) $ | (3) |
式中,φ为学习强度;r1和r2为[0, 1]内均匀采样的随机向量。第三项梯度增强信息Gradit+1用于加强粒子对局部区域的开发,计算方式如式(4)所示。式中,
| $ \left.\operatorname{Grad}_i^{t+1}=\frac{-\nabla f\left(X_i^t\right)}{\left|\nabla f\left(X_i^t\right)\right|} \right\rvert\, r V_i^t+\text { Interact }_i^{t+1} \mid $ | (4) |
5.模型及算法参数设置:优化模型中的结构权重除θRLRF设为2外,其余θR均设为1;平滑项权重γ设置为0.1。此外,本研究利用罚函数法将优化模型转化为无约束优化问题进行求解。GradRCIPSO的种群大小N和学习强度φ分别设置为900和0.3,终止准则设为满足f(Xt)-f(Xt+5)≤10-6。为得到权重参数c1、c2和c3的最佳参数组合,本研究将它们分别设置为0.1∶0.1∶1并采用CEC2010大规模优化基准测试集对各个参数组合进行测试[9]。经Friedman检验分析得到当c1、c2和c3分别设为0.6、0.6和0.8表现出最佳的平均性能。
6.统计学处理:应用SPSS 22.0软件进行数据分析。经检验相关数据分布不符合正态分布,数据以M(P25,P75)表示,并对各指标进行配对样本Wilcoxon秩和检验评估。P < 0.05为差异有统计学意义。
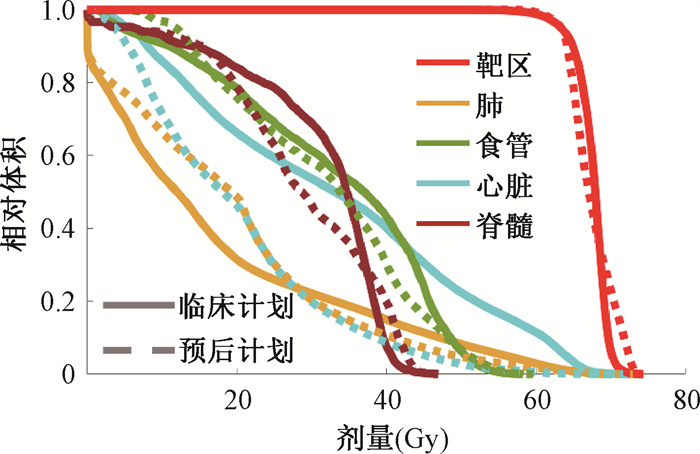
结果1.优化所得计划与临床计划的质量比较:本研究建立的放疗计划新优化方法GradRCIPSO可以成功生成基于预后引导的放疗计划(预后计划)。与临床计划相比,GradRCIPSO优化所得的预后计划可以在不损失剂量统计水平的基础上,有效降低患者的预期放疗风险。以其中病例7为示例所见(图 3),预后计划和临床计划靶区覆盖相当,D95%分别为63.41和63.43 Gy。在此基础上,患者放疗的预期总风险从1.83降至1.58,其中以CE3+发生率降低最为明显,从43.92%降至19.03%。综合优化的全部10例计划来看(表 1),预后计划和原临床计划的物理剂量指征项的统计水平基本保持相当,而放疗预期总风险得到明显改善(z=2.81,P < 0.01),从原临床计划的1.22(0.84, 1.51)降至0.93(0.80, 1.29),其中ARIE2+的预期风险改善最多,从[40.79(0.6, 62.96)]%降至[3.43(0.35, 53.72)]%。
|
图 3 病例7预后计划和临床计划的DVH Figure 3 The dose-volume histogram (DVH) for the prognosis-guided IMRT and clinical plans for Case 7 |
|
|
表 1 预后计划和临床计划的剂量学和预后比较[M(P25, P75)] Table 1 Comparison of dosimetry and prognosis between prognosis-guided IMRT and clinical plans [M(P25, P75)] |
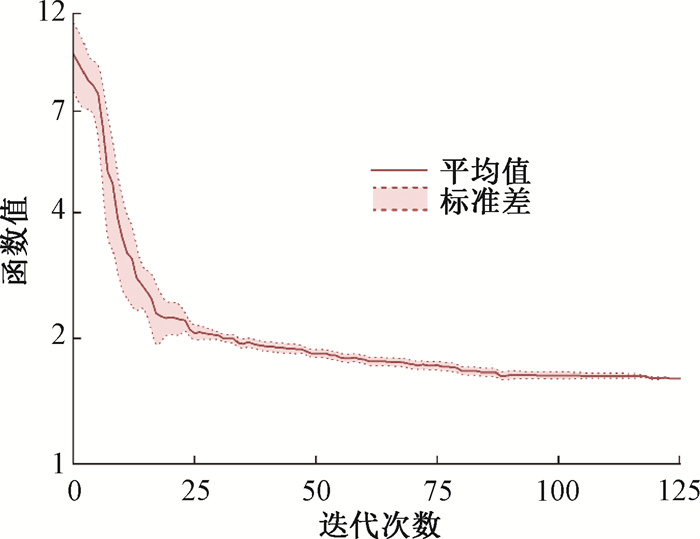
2.GradRCIPSO优化算法的收敛稳定性:为评估算法的收敛稳定性,本研究为每位患者多次重复性地生成计划,并观察同一计划在不同次优化间的收敛曲线的差异。图 4展示了其中一例患者分别生成10次计划的优化迭代收敛曲线。可见,由于算法存在初始状态、过程演变等的多重随机性,多次重复性生成同一患者计划,在不更改任何超参条件的情况下,其优化过程的迭代曲线不尽相同,但随迭代进行,不同次优化间的差异逐渐减小,最终趋于重合(std=0.002)。该现象在所验证的10例患者计划中均有所体现,这说明,尽管在迭代初期由于随机性导致不同次序优化之间存在较大差异,但随着迭代的进行,粒子群对解空间的探索变得足够充分,GradRCIPSO算法均能稳定收敛到相同的解。
|
图 4 病例8采用GradRCIPSO优化10次的迭代曲线 Figure 4 Curves after 10 iterations of optimization using GradRCIPSO for Case 8 |
3.与同类优化求解算法的性能比较:本研究将每一例放疗计划分别通过所提优化算法以及积极集、序列二次规划(sequential quadratic programming, SQP)、内点法、梯度下降法和RCIPSO优化算法进行优化求解并评估它们的优化性能,性能比较指标包括目标函数收敛函数值、优化求解效率以及优化所得计划预期风险质量。表 2列出了各算法的优化性能,其中以GradRCIPSO为基准,分析其在各性能指标中与其余算法的差异。结果显示,GradRCIPSO求解目标函数的收敛精度显著优于其他4种梯度算法(z=2.80~2.81,P < 0.01),与非局部梯度增强的RCIPSO相当。同时,GradRCIPSO优化所得计划相较于积极集、SQP、内点法和梯度下降法优化所得计划的放疗预期总风险均有显著性降低(z=2.80~2.81,P < 0.01)。而与RCIPSO相比,GradRCIPSO可保证同精度水平的求解质量(P>0.05),但求解时效性大大增强,耗费时间从[83.75(37.78, 184.2)] min降至[27.65(16.8, 37.2)] min。
|
|
表 2 不同算法的优化性能比较 Table 2 Comparison of optimization performance of different algorithms |
讨论
目前的放疗计划临床标准,采用基于群体统计剂量指标的目标函数,并未充分考虑患者的个体风险因素。此外,这些基于物理剂量的目标函数需要计划设计者主观地为每个剂量惩罚项分配权重,高度依赖经验和专业知识[18]。通过在目标函数中纳入预后模型可以根据患者的受照剂量和个性化信息量化患者的预后,从而更直观地平衡患者潜在的疗效和风险。但是,预后模型的纳入大大增加了计划的优化复杂度,导致现在临床计划优化常用的基于梯度的求解算法不再适用。为了解决这一问题,有研究引入了穷举搜索算法[19]或PSO算法[20-21]直接对优化模型进行求解,这些算法虽然可有效求解非凸问题,但仅适用于三维适形放疗的低维优化场景。还有研究通过将优化模型松弛为分段线性问题后再采用传统的数值方法求解[6],这种方法虽然可推广至IMRT,但模型的近似不可避免地引入一定误差。基于此,本研究提出了一种基于梯度增强的群体智能算法GradRCIPSO,以更高效、准确地解决IMRT预后引导放疗中的计划优化问题。具体地,GradRCIPSO通过让粒子同时学习群体交互信息和最速下降方向信息,结合了启发式算法的全局寻优能力和梯度算法的局部搜索能力。本研究在10例NSCLC病例的预后计划优化中验证了所提算法的性能。
结果显示,本研究提出的优化算法GradRCIPSO可以成功地为患者生成预后计划,其求解精度显著优于4种常用的梯度算法,且对初始点的选择具有更高的鲁棒性。这表明在预后计划优化中,群体智能算法比梯度算法更加适用。这是由于预后模型给优化目标带来了非凸性,而梯度算法容易陷入局部极值无法寻得其他优质计划。此时,不同的初始点会引导梯度算法优化至不同的局部极值,导致其对初始点的选择敏感性高[22]。相比之下,群体智能算法通过群体交互和随机搜索可以探索整个解空间[9],因此,初始点的不同对该类算法的影响较小。在与RCIPSO的对比中发现,GradRCIPSO可以在维持解质量的同时提升约3倍的优化速度。这是因为RCIPSO是一种完全基于随机搜索的方法,需要通过的大量的函数评估提高粒子对目标函数景观的认知。而GradRCIPSO通过引入确定性的梯度信息,使粒子能够直接学习局部邻域景观,从而减少了所需的函数评估次数,达到减少优化时间的目的。此外,GradRCIPSO通过粒子对群体交互信息的学习保留了RCISPO的全局寻优能力。
预后计划和临床计划的比较结果显示,在所有病例中,预后计划不仅满足了靶区处方剂量覆盖的要求,还有效降低了患者的放疗预期总风险,这主要通过降低患者的LRF2y和ARIE2+风险实现。然而,相比于临床计划,预后计划有增加RILT3+风险的趋势(z=-2.49,P=0.013)。这是因为在这10例病例中,RILT3+的预期风险相对较低,通过小幅提升该风险可以更大程度地降低计划的整体治疗风险。在具体的临床工作中,该问题需要联合医生对患者具体情况具体分析:如果更关注患者RILT3+的发生,那么可以通过提高RILT3+的权重或拉紧肺剂量约束来进一步降低RILT3+发生率;如果更关注患者整体的预后风险,那么肺部剂量的小幅上升对于总风险的降低来讲是获益的。这一结果表明,基于预后的优化方式有潜力取代传统基于剂量驱动的优化方式。因为基于剂量的优化仅依赖于离散的剂量指标,这些指标只传递了关于真实剂量-反应函数的有限信息,并不能完全代表真正的剂量-响应关系[23-24]。此外,本研究虽然通过剂量体积约束将脊髓最大剂量限制在50 Gy以内,但相较于临床计划,预后计划的脊髓最大剂量有所提高(z=-1.83,P=0.066),这是由于目标函数中缺乏脊髓的预后模型导致的。
本研究针对IMRT的预后计划优化求解提出了一种新的优化算法GradRCIPSO,该算法可同时兼顾优化求解的精度和效率。尽管如此,本研究未来仍需要引入新的方法以进一步缩短优化时间,提高临床工作效率。其次,在预后引导优化中,对于缺乏毒性模型的OAR,目前只能通过剂量约束来限制其剂量在安全范围以内,这有可能导致约束过松,无法将剂量降至最低。未来希望通过动态约束调整来解决这一问题。
利益冲突 所有作者声明不存在利益冲突
作者贡献声明 刘嘉雯负责设计研究方案、研究实施及论文撰写;李永宝负责收集临床数据;李华莉协助文献查找及数据分析;周凌宏、宋婷提出研究思路,指导论文修改
| [1] |
Modiri A, Vogelius I, Rechner LA, et al. Outcome-based multiobjective optimization of lymphoma radiation therapy plans[J]. Br J Radiol, 2021, 94(1127): 20210303. DOI:10.1259/bjr.20210303 |
| [2] |
Li P, Taylor J, Kong S, et al. A utility approach to individualized optimal dose selection using biomarkers[J]. Biom J, 2020, 62(2): 386-397. DOI:10.1002/bimj.201900030 |
| [3] |
Scott JG, Sedor G, Scarborough JA, et al. Personalizing radiotherapy prescription dose using genomic markers of radiosensitivity and normal tissue toxicity in NSCLC[J]. J Thorac Oncol, 2021, 16(3): 428-438. DOI:10.1016/j.jtho.2020.11.008 |
| [4] |
Hoffmann AL, den Hertog D, Siem AY, et al. Convex reformulation of biologically-based multi-criteria intensity-modulated radiation therapy optimization including fractionation effects[J]. Phys Med Biol, 2008, 53(22): 6345-6362. DOI:10.1088/0031-9155/53/22/006 |
| [5] |
Nahum AE, Uzan J. (Radio)biological optimization of external-beam radiotherapy[J]. Comput Math Methods Med, 2012, 2012: 329214. DOI:10.1155/2012/329214 |
| [6] |
Polan DF, Epelman MA, Wu VW, et al. Direct incorporation of patient-specific efficacy and toxicity estimates in radiation therapy plan optimization[J]. Med Phys, 2022, 49(10): 6279-6292. DOI:10.1002/mp.15940 |
| [7] |
Modiri A, Stick LB, Rice SR, et al. Individualized estimates of overall survival in radiation therapy plan optimization - A concept study[J]. Med Phys, 2018, 45(11): 5332-5342. DOI:10.1002/mp.13211 |
| [8] |
Houssein EH, Gad AG, Hussain K, et al. Major advances in particle swarm optimization: theory, analysis, and application[J]. Swarm Evol Comput, 2021, 63: 100868. DOI:10.1016/j.swevo.2021.100868 |
| [9] |
Yang Q, Song GW, Chen WN, et al. Random contrastive interaction for particle swarm optimization in high-dimensional environment[J]. IEEE Trans Evol Comput, 2024, 28(4): 933-949. DOI:10.1109/TEVC.2023.3277501 |
| [10] |
Li JY, Zhan ZH, Zhang J. Evolutionary computation for expensive optimization: a survey[J]. Mach Intell Res, 2022, 19(1): 3-23. DOI:10.1007/s11633-022-1317-4 |
| [11] |
Machtay M, Bae K, Movsas B, et al. Higher biologically effective dose of radiotherapy is associated with improved outcomes for locally advanced non-small cell lung carcinoma treated with chemoradiation: an analysis of the Radiation Therapy Oncology Group[J]. Int J Radiat Oncol Biol Phys, 2012, 82(1): 425-434. DOI:10.1016/j.ijrobp.2010.09.004 |
| [12] |
Dess RT, Sun Y, Matuszak MM, et al. Cardiac events after radiation therapy: combined analysis of prospective multicenter trials for locally advanced non-small-cell lung cancer[J]. J Clin Oncol, 2017, 35(13): 1395-1402. DOI:10.1200/JCO.2016.71.6142 |
| [13] |
Hawkins PG, Boonstra PS, Hobson ST, et al. Radiation-induced lung toxicity in non-small-cell lung cancer: Understanding the interactions of clinical factors and cytokines with the dose-toxicity relationship[J]. Radiother Oncol, 2017, 125(1): 66-72. DOI:10.1016/j.radonc.2017.09.005 |
| [14] |
Zhu J, Zhang ZC, Li BS, et al. Analysis of acute radiation-induced esophagitis in non-small-cell lung cancer patients using the Lyman NTCP model[J]. Radiother Oncol, 2010, 97(3): 449-454. DOI:10.1016/j.radonc.2010.09.025 |
| [15] |
Breedveld S, Storchi PR, Keijzer M, et al. Fast, multiple optimizations of quadratic dose objective functions in IMRT[J]. Phys Med Biol, 2006, 51(14): 3569-3579. DOI:10.1088/0031-9155/51/14/019 |
| [16] |
Deasy JO, Blanco AI, Clark VH. CERR: a computational environment for radiotherapy research[J]. Med Phys, 2003, 30(5): 979-985. DOI:10.1118/1.1568978 |
| [17] |
NCCN clinical practice guidelines in oncology-non-small cell lung cancer(2024 Version 5)[R/OL].2024. http://www.nccn.org.
|
| [18] |
杨晓喻, 赵于前, 杨振, 等. 基于元启发策略的肿瘤调强放疗自动计划方法[J]. 中华放射医学与防护杂志, 2023, 43(1): 15-22. Yang XY, Zhao YQ, Yang Z, et al. A metaheuristics-based automatic planning method for intensity-modulated radiation therapy[J]. Chin J Radiol Med Prot, 2023, 43(1): 15-22. DOI:10.3760/cma.j.cn112271-20221012-00406 |
| [19] |
Wilson LJ, Newhauser WD. Generalized approach for radiotherapy treatment planning by optimizing projected health outcome: preliminary results for prostate radiotherapy patients[J]. Phys Med Biol, 2021, 66(6): 065007. DOI:10.1088/1361-6560/abe3cf |
| [20] |
Stick LB, Vogelius IR, Modiri A, et al. Inverse radiotherapy planning based on bioeffect modelling for locally advanced left-sided breast cancer[J]. Radiother Oncol, 2019, 136: 9-14. DOI:10.1016/j.radonc.2019.03.018 |
| [21] |
Rechner LA, Modiri A, Stick LB, et al. Biological optimization for mediastinal lymphoma radiotherapy - a preliminary study[J]. Acta Oncol, 2020, 59(8): 879-887. DOI:10.1080/0284186X.2020.1733654 |
| [22] |
Mathew M. A new gradient based particle swarm optimization algorithm for accurate computation of global minimum[J]. Appl Soft Comput, 2012, 12(1): 353-359. DOI:10.1016/j.asoc.2011.08.037 |
| [23] |
Deasy JO, Niemierko A, Herbert D, et al. Methodological issues in radiation dose-volume outcome analyses: summary of a joint AAPM/NIH workshop[J]. Med Phys, 2002, 29(9): 2109-2127. DOI:10.1118/1.1501473 |
| [24] |
朱健, 李宝生, 舒华忠, 等. 正常组织并发症概率模型综述[J]. 中国生物医学工程学报, 2014, 33(2): 233-240. Zhu J, Li BS, Shu HZ, et al. Review of normal tissues complication probability models[J]. Chin J of Biomed Eng, 2014, 33(2): 233-240. DOI:10.3969/j.issn.0258-8021.2014.02.014 |
 2025, Vol. 45
2025, Vol. 45


