核与辐射事故发生后,放射性气溶胶会随着呼吸作用进入体内形成内污染,常使用对全身或器官中放射性核素进行体外直接测量的方式对γ型内污染进行监测和分类[1],为下一步医学救援提供依据。肺计数器是上述体外直接测量方法中常用的测量仪器,通过对肺中沉积的放射性核素进行计数,进一步估算受污染人群摄入量和内照射剂量。肺计数器测量技术关键在于确定探测效率和最小可探测活度,其中效率刻度是保证人体内污染活体测量准确性的关键步骤,通过效率刻度可以获得探测器的计数与受污染人体内放射性核素的滞留量之间的关系[2]。然而吸入放射性气溶胶后,核素会随着人体代谢活动扩散至体内其他器官,从而对肺的效率刻度造成影响,目前常采用的放射性核素均匀分布的肺源作为效率刻度的物理模型,同时默认肺计数器计数结果仅仅来自于肺部器官进行估算内污染的方法会导致一定程度高估人体内污染的滞留量[3]。为探究在意外情况下吸入不同理化状态的放射性气溶胶后,核素分布对肺计数器效率刻度的影响,本研究根据国际放射防护委员会(ICRP)核素代谢系列报告,计算吸入含有235U的气溶胶后,放射性物质在体内随时间变化的分布情况后,基于Geant4蒙特卡罗计算软件结合ICRP 145号报告[4]中的人体网格型参考计算模型编写了肺计数器内污染效率刻度程序,通过无源效率刻度方法对肺计数器进行效率刻度,结合感兴趣器官中放射性核素的滞留份额对肺计数器进行动态效率刻度,研究核素分布对肺计数器效率刻度的影响。
材料与方法1. 核素代谢计算方法:为了合理并且简便地估算放射性核素进入体内后由于器官的机械运动和生物代谢后的分布情况,ICRP将体内的器官和组织简化为隔室模型,只需考虑放射性核素在各个器官内的转移速率而不需要考虑具体的转移方式、器官形态等问题[5]。
放射性物质与空气中的气溶胶粒子结合后经过口鼻进入呼吸道后,在鼻腔中的鼻毛、上呼吸道中的黏膜等组织的过滤作用下,沉积在呼吸道表面,沉积的份额受微粒的大小、形态、密度以及解剖学生理学等参数影响。沉积在呼吸道中的放射性物质有两种廓清机制即:通过吞咽、擤鼻和经由淋巴进入淋巴结机械廓清机制和直接吸收进入血液的入血廓清两种方式清除。根据吸收入血的速率不同,ICRP将不同化学形式的放射性物质分为F型(快速)、M型(中速)、和S型(慢速)。
全身循环模型是描述放射性核素进入体循环后在体内各个组织或器官中随着时间滞留和分布的模型,和呼吸系统以及消化系统的动力学模型不同的是,全身放射性核素生物动力学模型描述的是特定元素的模型结构和参数值,而不是一个通用的模型。
本研究根据文献[6]中的呼吸系统转移系数和文献 [7]中消化系统的转移系数,以及文献 [8]中铀的全身循环系统的转移系数对单次摄入含有235U的放射性微粒在体内滞留转移的规律,计算了从事轻体力工作的鼻呼吸习惯的成年男子,在吸入活性中值空气动力学直径(activity median aerodynamic diameter,ADAM)为5和1 μm的F、M、S型几种理化状态的放射性物质后,放射性核素在体内的分布。
ICRP隔室模型中假设放射性核素在隔室j中放射性核素的滞留量由上一隔室i的转入量和向下一隔室k转出量以及放射性核素的衰变量决定,其中由于存在部分隔室之间存在反馈情况,上一隔室i以及下一隔室k可能为相同隔室。在任意隔室中传递的过程可以使用一阶微分方程表示:
| $ \frac{{d{A_j}\left( t \right)}}{d} = \sum\limits_j {{\lambda _{i, k}}{A_i}\left( t \right) - \sum\limits_j {{\lambda _i}{A_j}\left( t \right) - {\lambda _p}{A_j}\left( t \right)} } $ | (1) |
式中,i, j, k为隔室,λi, j为上一隔室j到隔室i的传递系数,λi, k为隔室i到下一隔室k的传递系数,λp为核素的衰变系数。
根据上述任意隔室中核素滞留量随时间变化的微分方程,构建235U隔室模型的微分方程组,通过解矩阵的方式进行求解。
2. 模型设计:γ放射性内污染体外直接测量常用闪烁体探测器(碘化钠、溴化镧)或半导体(高纯锗)探测器进行。其中溴化镧闪烁体探测器是由LaBr3掺杂少量激活性Ce3+组成的,具有高能量分辨率,稳定的温度特性,高闪烁光输出以及短响应时间等特性[9]。本研究采用无源效率刻度方法,使用蒙特卡罗法对探测器进行效率刻度,建立了一个探头尺寸为51 mm × 56 mm的溴化镧探测器模型开展研究,其中包层材料为双铝材料,包层在探测器顶部厚度为1 mm,侧壁厚度为1.5 mm,晶体反射层材料为聚四氯乙烯,厚度为0.5 mm,光导材料为SiO2厚度为11 mm。并使用60Co与137Cs标准源进行实源实验,通过调整晶体尺寸,结果表明当γ射线能量为662 keV时计算值与实验值相对能量偏差为4.3%,当γ射线能量为1 173 keV时计算值与实验值相对能量偏差3.1%。
模拟使用的人体模型是ICRP 145号报告[4]中的男性成人四面体网格型参考计算体模。四面体网格参考计算模型可以直接在蒙特卡罗代码中实现,避免了前期体素模型体素化的过程,具有分辨率高,模型具有连续性等优点[4]。假设放射性核素摄入后,在体内代谢活动作用下,放射性核素在上述源器官中均匀分布,选取了前鼻道、后鼻道、肺、肝脏、胃、小肠、左结肠、右结肠、直肠乙状结肠、肾脏、膀胱作为源器官,进行效率刻度模拟实验。
由于放射性核素在体内器官中的滞留量随时间变化,可以通过动态效率刻度方法,将肺计数器对不同器官的探测效率结合器官中放射性核素滞留量随时间变化的规律,根据动态效率刻度计算公式通过将蒙特卡罗模拟获得的计数器对不同器官的探测效率与相应的器官结合获得刻度值:
| $ \varepsilon \left( t \right) = \sum {{y_a}\left( t \right)} {\varepsilon _a} $ | (2) |
式中,a为器官,ya(t)为器官i中随时间变化的滞留量,εa为肺计数器对器官a的探测效率。
结果1. 核素代谢计算结果:由于ICRP有关铀代谢模型并没有给出全部器官的具体代谢模型,本研究选取了部分器官开展研究,由于选取的感兴趣器官在本研究选取的100 d内核素的滞留量占总滞留量的89%以上,故认为意外吸入含铀微粒后,核素全部滞留在上述感兴趣器官中。计算结果见图 1。

|
图 1 摄入不同理化性质235U化合物后器官滞留份额A~B. 分别摄入1和5 μm,F型;C~D. 分别摄入1和5 μm,M型;E~F. 分别摄入1和5 μm,S型 Figure 1 Retention fractions in organs after ingestion 235U compounds with different physicochemical properties A-B. After ingestion of 1 and 5 μm, respectively, F type; C-D. After ingestion of 1 and 5 μm, respectively, M type; E-F. After ingestion of 1 and 5 μm, respectively, S type |
不同粒径的放射性微粒在呼吸系统中不同部位的沉积不同,对于粒径为5 μm的放射性微粒,摄入初期在鼻咽区有着较高的滞留水平,沉积在肺部的放射性微粒仅占呼吸系统沉积量的10%,对于粒径为1 μm的放射性微粒,单次吸入后沉积在肺部的份额占在呼吸系统沉积量的26.4%。摄入3 d后鼻咽区的放射性微粒几乎全部清除,咽部区沉积的放射性微粒清除到消化系统后使得消化系统中的滞留份额升高。吸收类型为F型的化合物在摄入后1 d在肺部的沉积几乎全部清除,而吸收类型为M和S型化合物会在肺部中长期滞留。
为了验证计算结果,本研究与ICRP参考值[7]作对比,结果列于表 1。
|
|
表 1 自编程序对单次吸入5 μm M类235U气溶胶全身滞留量计算值的正确性检验 Table 1 Validation of the calculation of whole-body retention after a single inhalation of 5 μm M type 235U aerosol using a self-developed program |
由表 1可知,本研究计算结果与ICRP系列文件[4-8]提供的参考值基本相同,最高误差1.67%,可能是文献 [10]中提到的不同数值解法在此时间点的微小差异经由四舍五入进位后差异扩大造成,因此认为本研究编程方法和程序正确。
2. 蒙特卡罗模拟:本研究采用Geant4程序包,进行探测器效率刻度计算,Geant4是一款基于蒙特卡罗方法,主要用于模拟各种粒子输运过程及其与物质相互作用的软件程序。模拟计算探测器对不同器官中235U(γ光子能量185.7 keV)的响应[11-13]。在模拟计算过程中,考虑了光电作用、电子对效应和康普顿散射的物理过程,使用所构建的探测器模型对准参考计算模型背部右肺中心位置,距离背部的测量距离为1 cm,对不同器官中滞留的235U进行效率刻度模拟计算,模拟粒子数为108,模拟计算结果误差 < 3%。为了更加直观地观察核素分布对肺计数器探测效率的影响,将对不同器官的效率刻度结果进行归一化,以肺计数器对肺的计数效率为1,前鼻道、后鼻道、肝、肾、膀胱、胃、小肠、左半结肠、右半结肠、乙状结肠计数效率分别为0.042 9、0.137、0.335、0.332、0.033 8、0.041 2、0.125、0.161、0.114和0.058 8。
从图 2中可以看出,距离肺部越近的器官,肺计数器计数效率越高,将前期计算获得的放射性核素在器官中随时间变化的滞留量与相应的对肺计数器计数效率结合,获得肺对应的对肺计数器探测效率的贡献随时间的变化,计算结果见图 3。
|
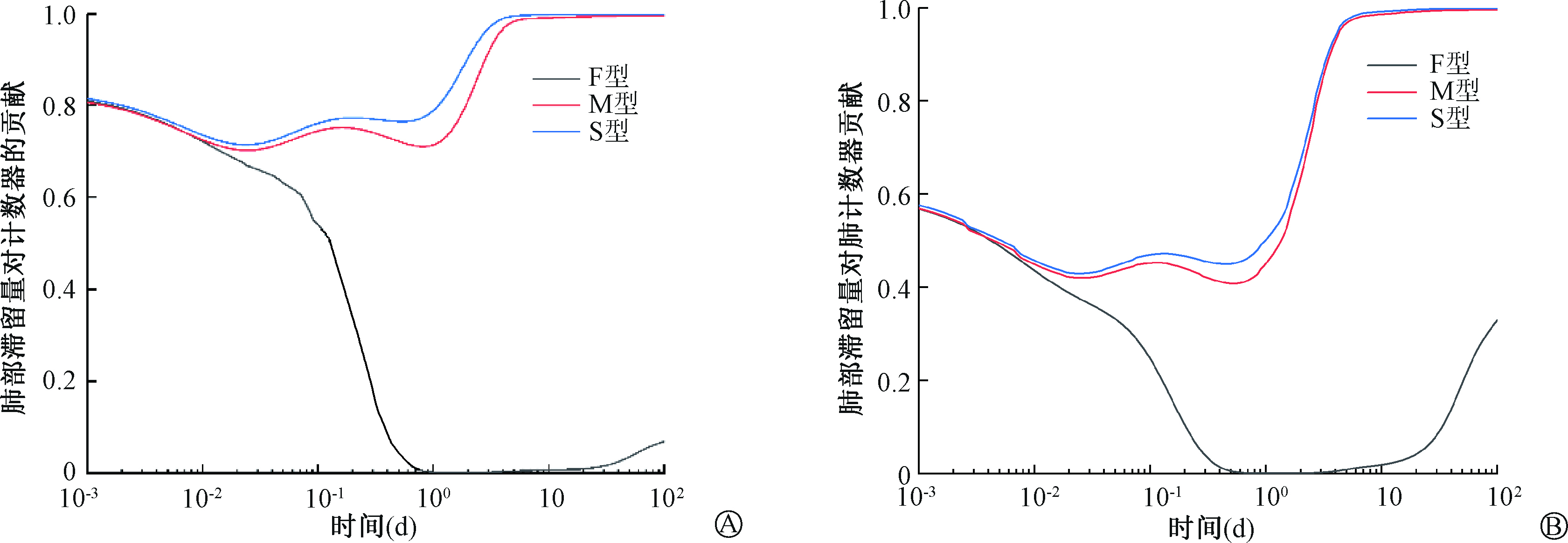
图 2 吸入1(A)和5 μm(B)气溶胶肺部滞留量对肺计数器贡献 Figure 2 Contribution of lung retention of inhaled aerosols of diameter 1 μm(A) and 5 μm(B)to the lung counter |
|
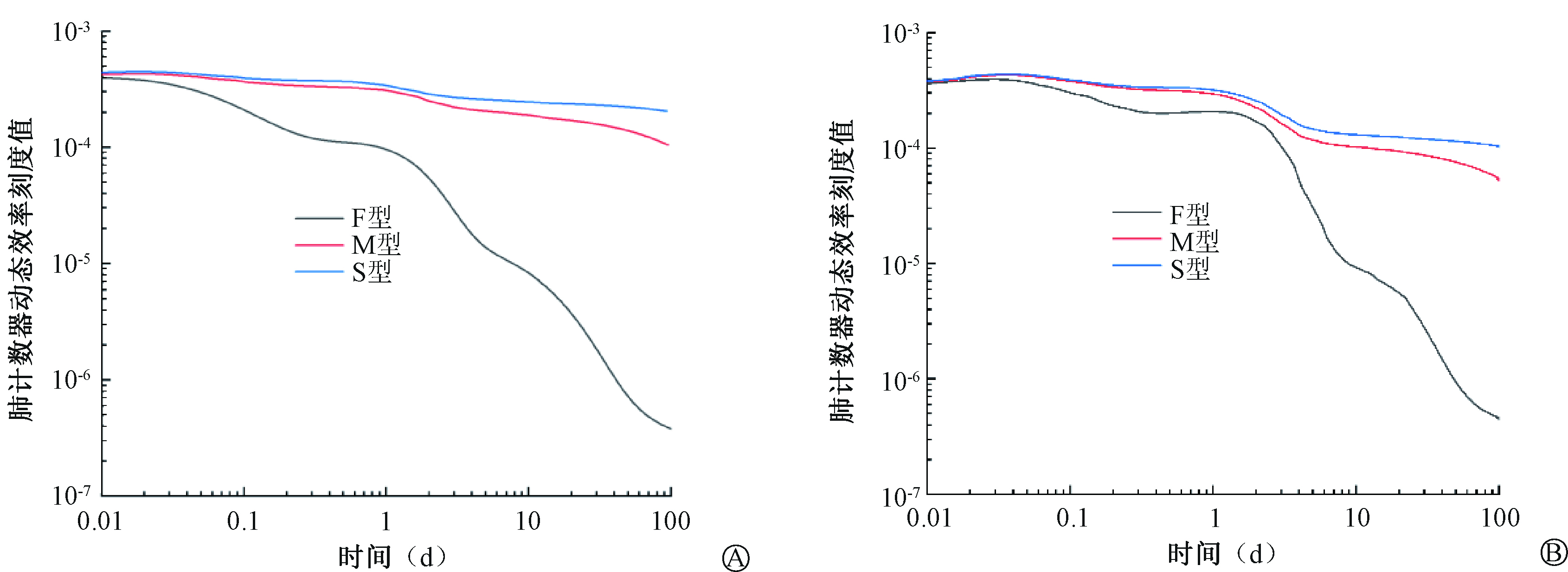
图 3 摄入1(A)和5 μm(B)气溶胶后肺计数器动态效率刻度值 Figure 3 Dynamic efficiency calibration values of the lung counter after ingesting 1 μm(A) and 5 μm(B)aerosols |
不同粒径的放射性气溶胶在呼吸系统中的沉积情况不同,粒径小在肺部的沉积量相对较多,从而对肺计数器计数的份额贡献较多。在单次吸入放射性气溶胶初期,放射性微粒在鼻咽区有较高水平的沉积,肺计数器计数主要来源于此处。随着沉积在鼻咽区的放射性核素被快速清除到体外和消化道中,肺部滞留的放射性核素对肺计数器计数贡献份额增加。对于吸收类型为F型的235U化合物,肺部区域滞留的放射性核素经由入血廓清快速吸收至内环境,对肺计数器的贡献份额随时间迅速下降,当ADAM为1 μm时,8 h后肺部区域滞留份额对肺计数器计数的贡献份额 < 10%;当ADAM为5 μm时,5 h后肺部区域滞留份额对肺计数器计数的贡献份额 < 10%,在摄入50 d后肺部滞留份额对肺计数器计数贡献份额增加,但不超过30%。对于吸收类型为M型的235U化合物,当ADAM为1 μm时,在摄入后的3 d内,放射性微粒主要沉积在鼻咽区,肺计数器对肺部滞留量的计数占肺计数器总计数的70%~90%,由于放射性核素在鼻咽区代谢速率较快,在摄入3~100 d,肺部计数大于总计数的90%;当ADAM为5 μm时,在摄入3 d内,肺部滞留份额对肺计数器计数贡献占总计数的41%~83%,摄入3~100 d,肺部滞留量对肺计数器总计数贡献份额> 83%。对于吸收类型为S型的235U化合物,在摄入后的3 d内,由于沉积在鼻咽区放射性微粒的影响,当ADAM为1 μm时,肺计数器对肺部滞留量的计数占肺计数器总计数的71%~95%;当ADAM为5 μm时,肺计数器对肺部区域的滞留量计数占总计数的60%~ 88%。由于S型的235U化合物在肺部代谢速率缓慢,在摄入3~100 d内,当ADAM为1 μm时肺计数器对肺部区域的滞留量的计数大于总计数的95%;当ADAM为5 μm时,肺计数器对肺部区域的滞留量的计数大于总计数的88%。
为降低内污染估算过程中的误差,使用动态效率刻度计算公式获得肺计数器随时间变化的动态效率刻度,模拟计算获得的不同理化类型的235U化合物动态效率刻度结果件图 4。
讨论本研究根据ICRP核素代谢系列模型以235U为例,分别计算了单次吸入ADAM为1、5 μm的F型、M型、S型235U放射性物质后,核素在体内随时间的分布。使用ICRP 145号报告[4]中的人体网格型参考计算模型使用Geant4程序包模拟计算了肺计数器对不同器官的探测效率,以及肺部区域的核素滞留量对肺计数器贡献份额随时间的变化。研究结果表明,吸入放射性核素理化形态不同,吸入后的时间不同,在体内的分布不同,对肺计数器计数的影响不同。特别是在暴露初期或吸入F型化合物的情况下,若将肺计数器计数值直接视为肺部放射性核素滞留量,会导致内污染估算的严重高估。最后本研究使用蒙卡模拟计算获得的计数器对不同器官的计数效率结合核素在体内的代谢规律进行动态效率刻度计算,与传统的静态效率刻度方法相比,动态效率刻度方法能够更准确地反映摄入核素后,体内核素在不同时间下不同分布对应的计数器的计数结果,有效降低了内污染估算的误差。
本研究以单次急性吸入235U核素为例进行了模拟计算,得到不同时刻动态效率刻度结果。在ICRP系列出版物中[6-8]给出了所有核素的代谢隔室模型,本文所建立的计算方法可推广至其他各种放射性核素、不同摄入途径以及慢性放射性核素摄入等情况,并考虑个体差异(如性别、年龄、工作类型等)对核素分布的影响,从而进一步降低内照射估算误差。未来的研究还可以结合更多的实验数据,验证模拟结果的准确性,并探索更高效的计算方法。
利益冲突 所有作者声明无利益冲突
作者贡献声明 刘婕负责实验设计、模型搭建和文章撰写;纪云龙负责研究指导,数据分析;许旭、张晓敏负责数据计算、实验指导;李大伟、张宇心负责作图,资料整理,论文内容修改;宁静负责课题设计、论文审阅,经费支持
| [1] |
中华人民共和国卫生部. GBZ 129-2016职业性内照射个人监测规范[S]. 北京: 中国标准出版社, 2016. Ministry of Health of the People's Republic of China. GBZ 129-2016 Specifications for individual monitoring of occupational internal exposure[S]. Beijing: Standards Press of China, 2016. |
| [2] |
张晓敏, 李大伟, 纪云龙, 等. 基于蒙卡模拟方法的便携式现场肺计数器理论研究[J]. 军事医学, 2020, 44(7): 530-533. Zhang XM, Li DW, Ji YL, et al. Theoretical study of a portable field lung counter based on Monte Carlo simulation method[J]. Mil Med Sci, 2020, 44(7): 530-533. DOI:10.7644/j.issn.1674-9960.2020.07.010 |
| [3] |
刘立业. 中国成年男性参考人体素模型及在剂量测量评价中的应用[D]. 北京: 清华大学, 2010. Liu LY. Reference computational human phantoms for adult males in China and their application in dose measurement and evaluation[D]. Beijing: Tsinghua University, 2010. |
| [4] |
International Commission on Radiological Protection. ICRP Publication 145. Adult mesh-type reference computational phantoms [R]. London: SAGE, 2020.
|
| [5] |
International Commission on Radiological Protection. ICRP Publication 130. Occupational intakes of radionuclides: Part 1[R]. London: SAGE, 2015.
|
| [6] |
International Commission on Radiological Protection. ICRP Publication 100. Human Alimentary Tract Model for Radiological Protection[R]. Oxford: Elsevier, 2006.
|
| [7] |
International Commission on Radiological Protection. ICRP Publication 134. Occupational intakes of radionuclides: Part 2[R]. London: SAGE, 2016.
|
| [8] |
International Commission on Radiological Protection. ICRP Publication 137. Occupational intakes of radionuclides: Part 3[R]. London: SAGE, 2017.
|
| [9] |
邓中华, 王媛, 赵永生, 等. 溴化镧探测器效率刻度与晶体表征[J]. 核电子学与探测技术, 2018, 38(2): 250-253. Deng ZH, Wang Y, Zhao YS, et al. Efficiency calibration and crystal characterization of lanthanum bromide detectors[J]. Nucl Electron Detect Technol, 2018, 38(2): 250-253. |
| [10] |
陈倩兰, 骆志平, 夏益华. 利用不同呼吸道模型计算239Pu的肺部滞留量结果比较[J]. 中国辐射卫生, 2018, 27(2): 97-101. Chen QL, Luo ZP, Xia YH. Comparison of lung retention of 239Pu using different respiratory models[J]. Chin J Radiol Health, 2018, 27(2): 97-101. DOI:10.13491/j.issn.1004-714x.2018.02.001 |
| [11] |
Allison J, Amako K, Apostolakis J, et al. Recent developments in Geant4[J]. Nucl Instrum Methods Phys Res Sect A, 2016, 835: 186-225. DOI:10.1016/j.nima.2016.06.125 |
| [12] |
Allison J, Amako K, Apostolakis J, et al. Geant4 developments and applications[J]. IEEE Trans Nucl Sci, 2006, 53(1): 270-278. DOI:10.1109/TNS.2006.869826 |
| [13] |
Agostinelli S, Allison J, Amako K, et al. Geant4-a simulation toolkit[J]. Nucl Instrum Methods Phys Res Sect A, 2003, 506(2003): 250-303. DOI:10.1016/S0168-9002(03)01368-8 |
 2025, Vol. 45
2025, Vol. 45


