2. 北京大学未来技术学院,北京 100871;
3. 北京大学核物理与核技术国家重点实验室,北京 100871;
4. 香港理工大学医疗科技及资讯学系,香港 999077;
5. 北京大学肿瘤医院暨北京市肿瘤防治研究所放疗科,恶性肿瘤发病机制及转化研究教育部重点实验室,北京 100142
2. College of Future Technology, Peking University, Beijing 100871, China;
3. State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing 100871, China;
4. Department of Health Technology and Informatics, Hong Kong Polytechnic University, Hong Kong 999077, China;
5. Key Laboratory of Carcinogenesis and Translational Research (Ministry of Education/Beijing), Department of Radiation Oncology, Peking University Cancer Hospital & Institute, Beijing 100142, China
当代放疗技术在靶区内外形成的极高剂量梯度一旦脱靶,很容易造成肿瘤控制失败和危及器官损伤的严重后果[1]。计划验证和剂量监测也成为制约放疗实施精度的关键瓶颈之一。基于射野影像系统(EPID)对治疗出射束进行在线监测,能够同时反映设备机械、辐射束流、解剖结构等综合因素导致的总体剂量偏差[2-3],且相较于治疗前的计划验证和治疗后的回顾性数据分析[4]具有更好的时效性,不仅能为后续放疗计划制定提供剂量误差定量和定位依据,而且有望通过实时监测及时防止重大辐射事故的发生。
本研究面向在线自适应放疗的临床需求,基于深度学习技术提出一套在体剂量监测参考基准图像合成新方法,即生成与计划双能kV锥形束CT(DECBCT)解剖结构一致的兆伏级(MV)投影图像作为在体监测出射束剂量的参考值,具有简便、高效且不依赖厂家机密数据等潜在优势。受到新技术的伦理监管和患者数据等限制,本研究仅基于虚拟仿真实验进行了可行性验证和效果定量评估。
材料与方法1. 数据集构建
(1) 4D扩展心脏躯干(XCAT)模型:XCAT模型是由Duke大学的Segars等[5]开发的基于高度详细的男女全身解剖结构和生理运动数据构建的人体模型。本研究利用XCAT提供的体素化的特定光子能量下的3D线性衰减系数模体生成数据集,线性衰减系数由组织的元素构成和给定的光子能量计算得出。通过改变头的前后、左右、上下3个维度的尺寸,以及皮肤、肌肉、骨骼的厚度参数系数等,使所有参数均独立服从期望1、方差为0.1的正态分布,模拟出形态各异的60例模体的头部解剖结构,其中42例用于模型训练,18例用于效果验证。设置光子的能量为80和150 kV用于生成双能图像。由于XCAT目前支持的最高光子能量为1 MV,作为初步可行性技术探索,本研究利用1 MV模拟治疗用射线。基于XCAT模型分别给出相应能量下的人体各组织线性衰减系数,并以三维形式存储于二进制文件中。
(2) kV投影模拟:为模拟CBCT图像,本研究在矩阵实验室(MATLAB)中调用TIGRE工具包,参考Varian机载kV CBCT系统的几何参数,结合从真实患者kV CBCT数据中获得的202个投影角度,对上节生成的不同能量3D线性衰减系数模体进行投影,获得患者80和150 kV管电压下的双能CBCT投影,以及对应角度的MV EPID图像。本研究使用的kV CBCT系统几何参数为:全扇半弧(full fan/half trajectory),投影角度范围为170.25°至369.04°;1 540 mm源—探测器距离;1 000 mm源轴距;1 280×1 280探测器分辨率;0.336 mm× 0.336 mm探测器像素;256×256×65重建图像分辨率;1.083 2 mm× 1.083 2 mm× 2.004 5 mm重建图像体素。
(3) DECBCT双能分解:基于80和150 kV双能CBCT,选择骨骼和软组织作为基物质,采用Niu等[6]提出的迭代分解方法进行双能分解以获得物质组成比例和相对电子密度(RED)。基本原理如式(1)所示:
| $ \binom{\mu_{\mathrm{H}}}{\mu_{\mathrm{L}}}=\left(\begin{array}{ll} \mu_{1 H} & \mu_{2 \mathrm{H}} \\ \mu_{1 \mathrm{~L}} & \mu_{2 \mathrm{~L}} \end{array}\right)\binom{x_1}{x_2} $ | (1) |
式中,μH、μL分别为高能图像和低能图像像素的线性衰减系数;μ1H、μ1L分别为选定的基物质1在高能和低能下的线性衰减系数,μ2H、μ2L分别为基物质2在高能和低能下的线性衰减系数;x1、x2分别为该点基物质1、基物质2的组成百分比。解此方程得到x1、x2,将它们分别乘以各自物质的相对电子密度并线性相加,即可得到CT对应的RED。
以式(1)给出的直接双能分解的结果作为初始解,通过迭代方式抑制双能分解中产生的噪声。方法基于最优线性无偏估计原则,将分解图像的估计方差-协方差矩阵的逆矩阵作为惩罚权重包含在最小二乘项中,并引入正则化项,通过计算邻近像素值差异的平方来对图像进行平滑。在此过程中,为了保护图像边缘的清晰度,在分解前先对图像的边缘进行检测,使得这些部分在正则化项中权重较小。
2.嵌入SE模块的循环对抗生成网络(SE-CycleGAN):如图 1,为完成kV与MV投影域之间的转换,本研究在传统循环生成对抗网络CycleGAN的基础上[7],在生成器的残差块后加入了作为注意力机制的SE模块(SE block)[8],实现动态的通道维度特征再校准,使网络学会使用全局信息来强调对生成任务重要的特征、抑制不重要的特征。该网络包含两个生成器模块和两个鉴别器模块。本研究的前向循环通过生成器-MV(GMV)实现用双通道的80、150 kV图像合成MV图像(s-MV),随后通过生成器-kV(GkV)从s-MV生成循环的双通道kV图像;后向循环(backward cycle)通过GkV从MV图像生成合成的双通道kV图像(s2C-kV),随后通过GMV生成循环的MV图像。

|
注:GMV.生成器-MV;GkV.生成器-kV; GMV.鉴别器-kV;GkV.鉴别器-kV 图 1 嵌入SE模块的循环对抗生成网络结构图 Figure 1 Overall structure of SE-CycleGAN |
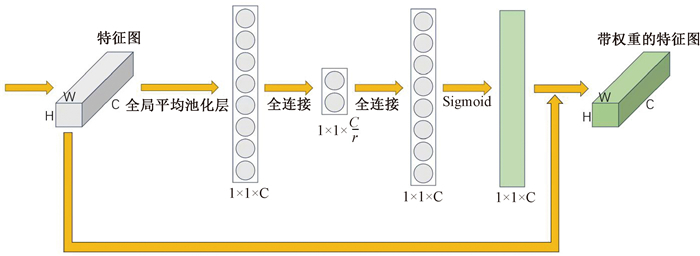
SE模块的具体结构见图 2。特征图首先经过一个全局平均池化层(GAP),将H和W维度压缩形成一维聚合特征,之后经过先降维再升维的两个全连接层,最后使用Sigmoid的激活函数使其成为0~1之间的权重向量,将权重向量与原特征图相乘,输出更新权重后的特征图。
|
注:H.特征图高;W.特征图宽; C.通道数 图 2 SE模块结构 Figure 2 Structure of the squeeze-and-excitation module |
在搭载两张NVIDIA TITAN RTX显卡的系统上进行网络训练,学习率设置为0.000 2,批量大小为10。训练在140轮后停止,此时各损失函数的值趋于平稳。在XCAT生成的模体中,42例共8 484组投影图像被用于训练,18例共3 636组投影图像用于测试。在测试集中,使用与80和150 kV解剖结构相同的MV图像作为真值评估合成MV图像的效果。
经TIGRE工具包正投方法生成的投影以二维图像的形式存储于matlab (即‘.mat’格式) 数据文件中。为保证图像质量不受损,本研究未将其转成图片格式(如‘.png’、‘.jpg’等)输入网络,而是直接载入matlab数据。在将数据转换为Tensor图之前,先对数据使用Min-Max归一化,在去除异常值的同时将数据归一到0~1之间。具体做法是,遍历不同能量的所有角度的投影图像,找出每张投影图像的98%分位像素值,并取所有图像中的最大值,将其四舍五入至小数点后一位设为Min-Max归一化的最大值,在本研究中该值为6.5;将0设为Min-Max归一化的最小值。随后,将所有数据统一乘以255,使所有像素值在0~255之间,在保留精度的同时,便于下一步的操作。
为对比本研究提出的SE-CycleGAN模型效果,同时比较以DECBCT作为输入的双通道网络和以RED作为输入的单通道网络效果,本工作还利用相同数据集同步进行了单通道CycleGAN和SE-CycleGAN网络的训练,并对两种模型和两种输入分别生成的MV图像精度进行了定量评估。
3.图像一致性评估参数:以XCAT直接生成的相同解剖结构的MV图像作为真值,使用如下定量参数评估模型由DECBCT图像合成MV图像的精度。MV图像真值的生成条件为:源-探测器距离1 540 mm;源轴距1 000 mm;探测器像素大小0.336 mm× 0.336 mm。
(1) 结构相似性指数(SSIM):衡量两张图像在亮度、对比度、结构方面的相似性,定义为:
| $ \operatorname{SSIM}(x, y)=\frac{\left(2 \mu_x \mu_y+C_1\right)\left(2 \sigma_{x y}+C_2\right)}{\left(\mu_x^2+\mu_y^2+C_1\right)\left(\sigma_x^2+\sigma_y^2+C_2\right)} $ | (2) |
| $ C_1=(0.01 L)^2, C_2=(0.03 L)^2 $ | (3) |
式中,x与y分别为合成MV图像和真值,两张图像的大小、分辨率一致;μx、μy分别为x和y的平均值;σx2、σy2分别为x和y的方差;σxy为x与y的协方差;C1、C2为维持稳定的常数;L为像素值的动态范围,在MATLAB中使用DynamicRange的值来指定L。
(2) 峰值信噪比(PSNR):衡量两张图像的一致性,由两张图像的最大像素值及其均方误差决定,定义为:
| $ \operatorname{PSNR}(x, y)=10 \log _{10}\left(\frac{\mathrm{MAX}^2}{\operatorname{MSE}}\right) $ | (4) |
式中,MAX为两张图像的最大像素值,MSE为均方误差。
(3) 均方根误差(RMSE):衡量网络生成的MV图像与真值图像对应位置的像素值差异,其定义为:
| $ \operatorname{RMSE}(x, y)=\sqrt{\operatorname{MSE}} $ | (5) |
| $ \operatorname{MSE}(x, y)=\frac{1}{M N} \sum\limits_{i=1}^M \sum\limits_{j=1}^N\left(y_{i j}-x_{i j}\right)^2 $ | (6) |
式中,M、N为图像宽度和高度方向的像素数量,xij、yij分别为两张图像在(i, j)位置上的像素值。
根据以上定义,更接近于1的SSIM、更大的PSNR和更小的RMSE值,均说明模型在合成准确的MV图像方面具备更优的表现。
4. 统计学处理:为比较4种网络结构生成MV图像的准确性,使用SPSS 27.0对测试集的3 636组生成图像和真值之间的SSIM、PSNR、RMSE值以x±s表示,分别进行正态性检验,对符合正态分布的数据进一步使用配对样本t检验,否则使用Wilcoxon符号秩检验。P < 0.05为差异有统计学意义。
结果1. 模拟图像:图 3展示了XCAT生成的不同光子能量下线性衰减系数模体,并选取了两个代表性角度展示了生成的CBCT投影图像,以及对应角度的MV图像真值。在展示的3个模体样例中,10号和30号模体来自训练集,50号模体来自测试集。

|
图 3 XCAT生成的不同模体CT图像,以及对应的3种能量和示例角度投影图 Figure 3 CT images of different phantoms and projections corresponding to three example angels under three energies generated using the XCAT model |
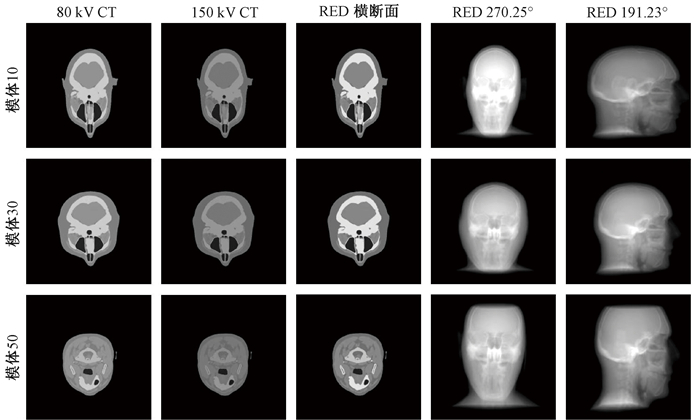
图 4展示了通过迭代双能分解方法[6]获得的RED图,以及使用前述方法对RED图像进行的投影结果,并分别输入单通道的SE-CycleGAN和CycleGAN网络进行了训练。
|
图 4 迭代双能分解生成的RED图像和示例角度RED投影 Figure 4 RED images of patients and the image RED projections at example angles generated using iterative dual-energy decomposition |
2. 网络训练结果:训练以DECBCT作为输入的SE-CycleGAN和CycleGAN分别用时1 658 min、1 796 min、以RED作为输入的SE-CycleGAN和CycleGAN分别用时1 736 min、1 804 min。测试3 636张投影平均总用时461.5 s,预测一张MV图像耗时约0.13 s。
图 5展示了不同网络和输入生成的MV图像比较。图 5(A~B)分别以DECBCT作为输入训练双通道SE-CycleGAN和CycleGAN,图 5(C~D)分别为以RED图像作为输入训练单通道SE-CycleGAN和CycleGAN。作为示例,图 5各行分别展示了测试集中第1、2、6号模体的代表性角度MV图像模型生成结果与真值的比较。其中第一列为通过网络生成的MV图像,第二列为真值MV图像。由于生成MV图像与真值的差异肉眼观察不明显,为了更加清晰地辨识二者差异的位置,将前二列的图像像素值差异取绝对值并放大20倍展示(

|
注:以3个测试集模体的代表性角度为例,分别输入DECBCT图像(A~B)和RED图像(C~D)时SE-CycleGAN和CycleGAN模型的生成结果。由于模型生成结果与真值差异(MV差异,子图集第三列)较小,为突出差异的位置分布,子图集第三列将差异放大20倍后进行展示( |
表 1定量展示了模型生成MV图像与真值图像之间的一致性评估结果。计算测试集18个模体(编号43~60)总计3 636张投影生成的MV图像与真值的差异,获得SSIM、PSNR、RMSE的平均值和标准差。表 1同时比较了SE-CycleGAN和CycleGAN分别以DECBCT和RED作为输入的训练结果。由于4种网络3个指标的所有结果均不符合正态分布,故使用Wilcoxon符号秩检验来评估结果的显著性。
|
|
表 1 模型生成MV投影的SSIM、PSNR、RMSE指标(x±s) Table 1 SSIMs, PSNRs, and RMSEs of MV projections generated using models(x±s) |
讨论
本研究定量展示了4种网络的一致性评估指标,其中SSIM非常接近于1,RMSE非常接近于0,PSNR也均高于文献[9]建议的阈值(35),这说明4种网络和数据组合方式均能生成良好的在体剂量监测参考MV图像。对比分析同一种输入类型的两种网络性能发现,加入注意力机制的SE-CycleGAN结果均优于传统Cycle-GAN。结合生成MV图像和真值图像的差异信息分析,原因可能是SE方法强调全局信息的获取,导致在大范围的亮度和对比度信息中SE-CycleGAN表现更佳。
对比同种网络结构、不同输入数据产生的结果发现,使用高低能CBCT投影图像作为双通道输入的训练效果优于使用RED投影图像作为输入的结果,尤其在180°附近更加明显。这可能是因为高低能CBCT投影图像包含更多原始数据,而双能分解获得的RED投影图像可能丢失了部分物质的信息。另一种可能的解释是RED“投影”实质上是电子密度的积分,与CBCT投影的线性衰减系数积分不同,它缺乏明确的物理意义,因此RED投影图像的特征与MV投影图像的特征之间的映射关系可能并不明确。但尽管如此,RED投影图像作为输入时生成的MV投影图像依然非常接近真值。通过调整网络参数,如图像预处理方式、SE模块的压缩比等,还有望进一步提升网络性能。
传统的剂量监测基准获取一般基于蒙特卡罗模拟预测EPID上出射束分布的理论[10-11],但此类方法需充分考虑准直系统、人体、支撑结构的吸收和散射及射线的强度调制和探测器能谱响应等复杂因素的影响,技术难度和硬件要求很高,且运算效率难以满足在线自适应放疗的需求。如Feng等[12]基于计划CT或从CT-Linac上获得的每日CT,使用蒙特卡罗方法计算出IMRT中参考的EPID图像,并依据图像引导(IGRT)的修正进行配准。蒙卡计算的过程主要包括使用光子和电子的相空间文件来生成EPID位置上的平面图像,随后在该图像上加入探测器响应和横向散射。最后,经过MU灰度校准以生成灰度图像。在质量控制(QA)或治疗的过程中,研究团队采集了所有的EPID图像,并在QA或治疗结束后与参考EPID图像进行γ分析。本研究从kV投影生成一个患者全部202个角度的MV投影仅耗时约30 s,远高于传统的蒙特卡罗模拟的效率,对设备和算力的依赖程度也更低,且不需要厂家公开模拟所需的详细技术参数,具有更好的灵活性和可及性。此外,深度学习在医学图像的模态转换和预测方面被大量的研究证明是准确和高效的[13-16],它也被用于辅助在体剂量监测参考图像的获取或剂量的计算[17-18]。为了将生成的MV图像进一步用作在体剂量验证,还需要在放疗计划文件中读取每个控制点对应的机架角度、剂量率、跳数、MLC叶片位置和射野形状等信息,并以此在MV图像上分割出相应的感兴趣区(ROI)并赋予剂量权重,最终得到一个剂量累积图像作为在体剂量监测的参考基准。通过和EPID在治疗过程中实时采集到的治疗出射束图像进行对比,有望及时发现并阻止由设备机械、辐射束流、患者因素等多种原因导致的重大剂量偏差。本研究提出的基于深度学习和双能CBCT的放疗在体剂量监测方法,有望为在线自适应放疗、立体定向放疗等先进的放疗技术提供更加精准的实时质控保障。与治疗前的验证、治疗后的回顾性重建和补救措施相比,本方法具有更好的时效性和安全性。对于无法进行实验测量的在线自适应放疗计划验证,本方法能够有效弥补基于计算验证的不足。
本研究的局限性在于其基于仿真模拟的实验设计,方法的可靠性有待未来获得伦理审批和临床数据后的进一步验证和改进。此外,为考虑散射线对EPID的影响以及不同加速器MV射线的能谱差异,未来还需基于更多真实患者数据进一步优化和验证深度学习模型,使其更好地平衡精确性与运算效率。
总之,本研究面向在线自适应放疗在体剂量监测临床需求,基于深度学习和DECBCT提出了一种创新的参考基准图像合成方法,并基于仿真模拟实验进行了可行性验证。本研究提出的SE-CycleGAN网络相较传统CycleGAN网络获得了更高的图像合成精度,运算效率和便捷度也远高于传统蒙特卡罗模拟方法。研究还发现直接使用DECBCT比使用RED作为网络输入的效果更优,为进一步技术开发和临床应用提供了方法和数据参考。
利益冲突 无
作者贡献声明 胡慧敏负责网络设计与论文撰写;董正坤参与实验设计和数据分析;余疏桐参与数据处理;林晨和黎田参与实验设计和论文修改;张艺宝负责实验设计和论文修改
| [1] |
Chargari C, Rassy E, Helissey C, et al. Impact of radiation therapy on healthy tissues[J]. Int Rev Cell Mol Biol, 2023, 376: 69-98. DOI:10.1016/bs.ircmb.2022.11.006 |
| [2] |
van Elmpt W, McDermott L, Nijsten S, et al. A literature review of electronic portal imaging for radiotherapy dosimetry[J]. Radiother Oncol, 2008, 88(3): 289-309. DOI:10.1016/j.radonc.2008.07.008 |
| [3] |
方家, 朱万里, 戴春艳, 等. 基于EPID在体剂量验证在肺癌和食管癌动态调强放疗中的应用研究[J]. 中华放射医学与防护杂志, 2023, 43(9): 705-711. Fang J, Zhu WL, Dai CY, et al. Application of EPID-based in vivo dose verification in dynamic intensity-modulated radiotherapy for lung and esophageal cancers[J]. Chin J Radiol Med Prot, 2023, 43(9): 705-711. DOI:10.3760/cma.j.cn112271-20230316-00078 |
| [4] |
Silvestri V, Raspanti D, Guerrisi MG, et al. Clinical implementation of a log file-based machine and patient QA system for IMRT and VMAT treatment plans[J]. Phys Med, 2023, 108: 102570. DOI:10.1016/j.ejmp.2023.102570 |
| [5] |
Segars WP, Sturgeon G, Mendonca S, et al. 4D XCAT phantom for multimodality imaging research[J]. Med Phys, 2010, 37(9): 4902-4915. DOI:10.1118/1.3480985 |
| [6] |
Niu T, Dong X, Petrongolo M, et al. Iterative image-domain decomposition for dual-energy CT[J]. Med Phys, 2014, 41(4): 041901. DOI:10.1118/1.4866386 |
| [7] |
Zhu JY, Park T, Isola P, et al. Unpaired image-to-image translation using cycle-consistent adversarial networks[C]. IEEE, 2017. DOI: 10.1109/ICCV.2017.244.
|
| [8] |
Hu J, Shen L, Albanie S, et al. Squeeze-and-excitation networks[J]. IEEE Trans Pattern Anal Mach Intell, 2020, 42(8): 2011-2023. DOI:10.1109/TPAMI.2019.2913372 |
| [9] |
Bull DR, Zhang F. Digital picture formats and representations[M]. Intell Image Video Comp (Second edition), 2021. DOI: 10.1016/B978-0-12-820353-8.00013-X.
|
| [10] |
Chytyk-Praznik K, VanUytven E, vanBeek TA, et al. Model-based prediction of portal dose images during patient treatment[J]. Med Phys, 2013, 40(3): 031713. DOI:10.1118/1.4792203 |
| [11] |
Zhang J, Cheng Z, Fan Z, et al. A feasibility study for in vivo treatment verification of IMRT using Monte Carlo dose calculation and deep learning-based modelling of EPID detector response[J]. Radiat Oncol, 2022, 17(1): 31. DOI:10.1186/s13014-022-01999-3 |
| [12] |
Feng B, Yu L, Mo E, et al. Evaluation of daily CT for EPID-based transit in vivo dosimetry[J]. Front Oncol, 2021, 11: 782263. DOI:10.3389/fonc.2021.782263 |
| [13] |
Azad R, Kazerouni A, Heidari M, et al. Advances in medical image analysis with vision Transformers: A comprehensive review[J]. Med Image Anal, 2024, 91: 103000. DOI:10.1016/j.media.2023.103000 |
| [14] |
Apostolopoulos ID, Papathanasiou ND, Apostolopoulos DJ, et al. Applications of generative adversarial networks (GANs) in positron emission tomography (PET) imaging: A review[J]. Eur J Nucl Med Mol Imaging, 2022, 49(11): 3717-3739. DOI:10.1007/s00259-022-05805-w |
| [15] |
Wolterink JM, Dinkla AM, Savenije MHF, et al. Deep MR to CT synthesis using unpaired data[J]. Lect Notes Comput Sci, 2017, 10557: 14-23. DOI:10.1007/978-3-319-68127-6_2 |
| [16] |
董正坤, 屈瑞, 余疏桐, 等. 基于稀疏重建锥形束CT和深度学习技术合成双能物质分解图[J]. 中华放射医学与防护杂志, 2024, 44(4): 317-322. Dong ZK, Qu R, Yu ST, et al. Synthesis of dual-energy material decomposition images based on sparse-view cone beam CT reconstruction and deep learning[J]. Chin J Radiol Med Prot, 2024, 44(4): 317-322. DOI:10.3760/cma.j.cn112271-20230825-00061 |
| [17] |
Bosco LD, Franceries X, Romain B, et al. A convolutional neural network model for EPID-based non-transit dosimetry[J]. J Appl Clin Med Phys, 2023, 24(6): e13923. DOI:10.1002/acm2.13923 |
| [18] |
Jia M, Wu Y, Yang Y, et al. Deep learning-enabled EPID-based 3D dosimetry for dose verification of step-and-shoot radiotherapy[J]. Med Phys, 2021, 48(11): 6810-6819. DOI:10.1002/mp.15218 |
 2025, Vol. 45
2025, Vol. 45


