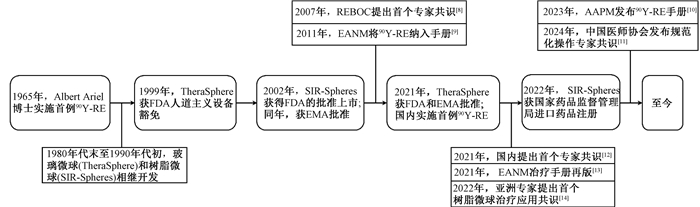
原发性肝癌位居全球恶性肿瘤发病率的第6位[1]。每年新发肝癌病例占全球总数的55%,多数患者确诊于中晚期且5年生存率低[2-3]。传统治疗手段的疗效常受瘤体体积和数量等因素的限制,相比之下,90Y微球放射性栓塞治疗(90Y microspheres radioembolization,90Y-RE)禁忌证少,适合原发性肝癌或肝转移、肝移植前辅助以及术后复发补救的治疗[4-6]。90Y-RE治疗已有近60年发展历史(图 1),目前已在近50个国家投入临床应用[7],2022年1月获我国国家药品监督管理局的进口药品注册批准。
|
注:FDA. 美国食品和药物管理局;EMA. 欧洲药品管理局;REBOC. 放射性栓塞近距离放射治疗肿瘤学联盟;EANM. 欧洲核医学协会;AAPM. 美国医学物理学家协会 图 1 90Y微球放射性栓塞治疗及专家共识的发展历史[8-16] Figure 1 The development of 90Y microspheres radioembolization and expert consensus[8-16] |
选择性内放射治疗(selective internal radiotherapy,SIRT)在治疗过程中,不可避免地会对健康肝实质或其他器官造成照射。因此,提高肿瘤应答率的同时,降低放射性并发症发生率,是剂量计划制定中的核心任务,精准的剂量估算对于优化治疗剂量方案至关重要。美国核医学会医学内照射剂量学(medical internal radiation dose,MIRD)委员会提出的内照射剂量计算方法,以其流程的简洁性和操作的便捷性,成为目前临床应用最为广泛的剂量估算方法。随着多模态融合技术的发展,直接蒙特卡罗法、体素S值以及局部能量沉积等精准估算手段,逐渐被应用于个体化90Y-RE治疗的剂量计划定制和验证。然而,目前尚缺乏剂量估算方法的共识性意见和行业规范,这在一定程度上限制了个体化剂量评价的发展和临床应用。为此,本文综述6种剂量估算方法的计算特性、应用效果及研究进展,旨在为形成个体化治疗剂量方案的共识、剂量预测与评估的标准化提供参考。
一、治疗原理90Y是一种半衰期为64.1 h的纯β衰变人工放射性核素,在两周内可释放约95%的能量[17]。衰变释放的β射线最高能量达2.27 MeV,平均能量为0.936 7 MeV,在组织内的最大射程为11 mm,平均穿透仅2.5 mm。这种特性使90Y在杀灭肿瘤细胞时,能够有效减少对周围非肿瘤组织的辐射损伤。由于人体对90Y没有特殊摄取的功能,游离的90Y会透过毛细血管网随血液分布于全身。因此,治疗通常将90Y搭载于结构稳定、耐辐照、直径均匀、密度适中易悬浮且具有良好生物相容性的微球颗粒上[18]。此外,放射性栓塞治疗的实施还依赖于肝脏及肿瘤的供血特征:肝脏实质75%~80%血供来自门静脉[19],而肝脏肿瘤主要由肝动脉供血[20]。通过选择性动脉插管将微球注入左或右肝动脉后,由于微球无法通过毛细血管床,以微球簇滞留于肿瘤微血管中[4],从而实现对肿瘤的精准剂量投递。
迄今为止,已有氧化钇、陶瓷以及生物相容性聚-L-乳酸等多种微球被报道[8, 16]。其中,玻璃微球TheraSpheres和树脂微球SIR-Sphere在临床中应用最广:SIR-Sphere直径约20~60 μm,可生物降解,比重小而便于制成悬浮液,单位微球放射性活度低,故治疗所需微球数量多、栓塞效果好,但易反流形成异位栓塞,增加非靶区域放射性损伤的发生率;TheraShperes直径约为20~30 μm,比重大、易沉积,常采用高压推注技术。与SIR-Sphere相比,在相同的靶区吸收剂量下,所需的微球数量较少,栓塞效果相对较差,且更易形成永久性栓塞,但异位栓塞概率低。目前,尚无随机对照试验的结果能明确支持这两种微球在临床疗效上存在显著差异[8]。
二、90Y微球治疗流程行栓塞治疗前,必须对患者进行全面筛查,以确定其是否适合接受治疗。为了预防微球流入肝动脉的内脏血管分支而引起放射性并发症,术前应实施肝血管造影和模拟栓塞,术后使用发射型计算机断层成像(emission computed tomography, ECT)定量90Y实际分布情况。治疗的主要流程与基本功能如下。
1. 患者筛选:在患者筛选环节,除了常规的体格、病史检查和体能状态评估之外,评价肝脏储备功能、肝肿瘤负荷以及总胆红素水平等禁忌证指标同样重要[9]。为确定正常肝实质的辐射耐受能力,临床常用Child-Pugh评分系统来评估肝脏储备功能[21]。医生根据临床经验裁量是否对肝脏储备有限、肾功能较差的患者实施手术。此外,肝内活动性感染、不可纠正的肝动脉-胃肠道动脉分流等绝对禁忌证由后续检查评估。
2. 常规影像学检查:对于符合术前安全要求的患者,医学影像检查是进一步定量评估肿瘤病灶的分布、数量、体积以及肝外疾病和肝硬化水平的重要手段。患者需在术前1个月内行动态增强CT或磁共振成像(magnetic resonance imaging, MRI)检查,并辅以正电子发射体层成像(positron emission tomography,PET)检查,全面获取肝脏及肿瘤特征。
3. 肝血管造影:为了确定微导管注射位置并预防90Y微球发生异位栓塞,术前采用数字减影血管造影术(digital subtraction angiography,DSA)绘制患者的肝动脉结构,以识别肝肿瘤供血血管、划定靶肝区域和异常交通血管。对于存在异位栓塞风险的内脏动脉、异常吻合以及动-静脉瘘[6],实施预栓塞以防止发生严重不良反应。有研究表明,锥形束CT(cone beam CT,CBCT)在识别供应血管和肝外血管方面或比DSA更为可靠[22],能够用于血管结构图像研究[23]。中国医师协会介入医师分会在《钇-90微球选择性内放射治疗肝脏恶性肿瘤规范化操作专家共识(2024版)》中明确推荐,在动脉造影术中使用CBCT检查,并结合术前常规影像学检查,以明确肿瘤部位、大小、数目及供血动脉情况。
4. 99Tcm-MAA模拟栓塞:99Tcm标记的大颗粒聚合人血清白蛋白(99Tcm-MAA)是一种尺寸在10~150 μm的可生物降解颗粒。由于生物分布与90Y微球相似,99Tcm-MAA常被用诊断作替代物。99Tcm-MAA的主要应用包括评估肺分流比例(lung shunt fraction,LSF)、识别消化道分流、辅助选取导管插管位置以及器官剂量预测[10, 24]。LSF为肺部与肺肝总计数之比,通常在注射后1~2 h内,使用平板或单光子发射计算机体层摄影(single-photon emission computed tomography,SPECT)获取[17],是重要的剂量计划和禁忌证评价指标。99Tcm-MAA与微球分布的一致性是剂量精准预测的基础,然而其等效性在近期研究中备受争议,但也有研究表明,即使在微球分布预测不准确的情况下,99Tcm-MAA所得剂量与肿瘤应答和总生存期等疗效评价指标仍表现出较好的相关性和预测价值[25]。
5. 制定治疗计划:医师在制定治疗方案时,综合考虑患者的肿瘤特征、实验室检查结果等因素,以确定治疗的类型,包括根治性、降期转化性或姑息性治疗。随后,根据方案类型制定剂量计划。美国医学物理师协会2023年发布的《90Y微球放射性栓塞实践指南》[10]建议的剂量计划制定的流程为:①注射替代性药物并使用平面或SEPCT/CT技术成像。②计算LSF。③根据预期疗效和危及器官剂量限值确定靶区吸收剂量。④基于靶区剂量推算施药活度。⑤估算肺部及非靶器官吸收剂量并调整施药活度。靶区吸收剂量的制定依据剂量-肿瘤应答等放射生物学模型,还受微球种类等因素影响[26-27]。然而,目前剂量参考值尚未定论。
推注活度(也称施药活度)即计划注射到靶区的放射性活度,通常依据计划的靶区剂量,多采用经验法、体表面积公式和分区模型等计算。经验法根据肿瘤与肝脏体积比(即肿瘤负担)“一刀切”地确定推注活度,因治疗副作用的安全边际较低而被放弃使用。体表面积法(body surface area,BSA)通过体表面积估算肝脏体积,依据肿瘤负担、LSF和肝功能调整活度,计算简便且具有良好的毒性耐受性[28]。但BSA忽略微球在肿瘤区域的优先分布且将活度人为限制在1.0~3.0 GBq,这使大型肿瘤面临治疗缺乏的风险。此外,体表面积与肝体积之间呈现低相关性,存在对肝体积正常的肥胖患者过量治疗,导致部分医疗实践放弃该方法。为进一步优化肿瘤应答率与放射性毒性,放射性摄入比等个体化校正因子和高个体化程度的计算模型被采用。因施药活度计算的本质是剂量估算的逆过程,个体化方法在第三节展开介绍。
6. 90Y-RE实施:为防止肿瘤血管的增生与重塑改变肝血管结构,治疗通常在术前影像检查完成后的2周内进行。治疗过程主要包括介入手术室准备、患者和器械准备、90Y微球输注与术中辐射防护等环节。术中再次进行动脉造影和CBCT扫描,以核准导管位置,确保血供区能够充分覆盖治疗靶区。
7. 术后评价:为验证90Y微球实际分布、预测疗效及并发症、收集与肿瘤特异性响应相关的临床资料,术后次日需评估患者靶区与危及器官剂量。90Y衰变伴发少量轫致辐射(2%~4%)[29]和正负电子对(0.021%)[7],可以采用SPECT/CT或PET/CT对90Y微球的分布和剂量进行定量可视化。成像模态的选择取决于具体的临床需求和研究目的,我国SPECT普及率高于PET而在术后评价中更常见。两种成像技术整体效果相似,但在低活度区域处理、噪声水平及对比度恢复等特定性能存在差异[30]。高质量的可视化数据是精准剂量评价的基础,剂量估算方法也是剂量评价的关键环节,后者相关的研究进展将在下一章节展开。
三、剂量估算方法90Y-RE治疗的剂量计算对于确定施药活度和进行术后剂量评价至关重要,估算方法包括MIRD方法、直接蒙特卡罗法、体素S值、剂量点卷积法和局部沉积法等。在临床实践中,MIRD方法因其简便性和标准化而广泛应用于施药活度的计算。其他方法更多用于术前活度分布的预测和术后剂量评价。蒙特卡罗模拟方法通过模拟大量随机事件来近似计算复杂系统的统计特性,是一种较为成熟的核医学剂量计算工具,常被视为剂量评价的“金标准”。
1. MIRD方法:基于放射性活度均匀分布的假设,MIRD方法将器官中累积活度与描述每单位累积活度在感兴趣区(region of interest,ROI)中平均吸收剂量的S值乘积以计算平均器官剂量,器官S值查阅MIRD手册获取[31]。微球在栓塞后位置相对固定,故累积活度仅与初始活度和物理半衰期有关,临床多采用MIRD方法(又称单房室模型)变式计算,如式(1):
| $ D=49.38 \times \frac{A_o}{m}(1-L S F) \times(1-R) $ | (1) |
式中,A0为推注活度,GBq;49.38为每GBq的90Y致单位质量组织吸收剂量,通常取50 Gy·kg·GBq-1 [19];靶肝质量m由患者肝脏体积乘密度(1.05 g/cm3)计算,kg;R为容器内残留活度占总施药活度的百分比,%。该方法因计算便捷而广泛用,个体化肝脏参数的引入使其较BSA容许更高的治疗活度。Sarwar等[32]在对60例患者的研究中发现,相同靶区吸收剂量下MIRD方法所得活度为1.7 GBq,远高于BSA的0.6 GBq,几乎未发生放射性并发症和不良反应。然而,微球在血管末端沉积和β射线短射程的特征,决定了肿瘤靶区将接受高于全肝平均的吸收剂量,单房室模型均匀分布的简化假设增加了低估肿瘤靶区剂量的风险[33-34]。此外,分流至肺部的放射性也会造成剂量估计偏差,偏离程度与肿瘤相对位置有关。Yildirim等[35]将90Y按LSF比例分配至肝、肺,根据患者肝脏体积和肿瘤位置对简单几何体模变形,发现该方法与直接蒙特卡罗模拟相比剂量偏差最高达16.18%。粗略的剂量评价导致其制定的治疗方案在临床中未表现出比单独使用化疗药物Sorafenib更好的预后[36-37]。
单房室模型的限制推动了支持单独评估肿瘤和正常肝脏剂量的多分区模型(partition model,PM)发展。PM将肿瘤、非肿瘤以及肺部分为3个单独的剂量室,采用99 mTC-MAA平板成像获取肿瘤/非肿瘤区域摄入比,以表征微球在肝脏内分布的相对差异[33]。复杂的剂量分布模型在合理提高推注活度的同时,未提高辐射诱导的肝毒性发生率[38]。Webster等[39]对同一治疗案例分别使用单房室和PM制定给药方案,前者在非靶肝实质的剂量(109 Gy)较后者高出约50%,达到诱发放射性肝炎的剂量阈值。
PM的可靠性源自99Tcm-MAA对微球空间分布的准确预测,现有报道对此尚存分歧。一项针对32名HCC患者的研究指出[40],PM与体素化蒙特卡罗计算的正常肝组织剂量结果几乎完全等效,而对肿瘤剂量估计的平均误差高达37%,低估严重。Woerner与Johnson[33]进一步指出肿瘤类型(单灶性与多灶性)与大小、前序治疗、推注速度和插管位置等均可影响微球和MAA的分布,MAA或与单灶性肿瘤中微球分布和剂量的一致性更高,注射时导管位置的偏移或引起至少30%的差异。Taebi等[41]用流体仿真证实了注射位置对微球分布影响,选用大叶和肝动脉注射时,输送到肿瘤的微球比例分别为22%和82%。此外,ROI的勾画也会影响剂量估算的准确度,肝脏肿瘤分区依赖于血管体区的精准识别,这对核医学科医生与介入医生的配合提出了较高的要求。缺乏对于除肺脏外周边器官的剂量评估也是PM的弊端之一。
2. 直接蒙特卡罗法:蒙特卡罗模拟(Monte Carlo simulation,MCs)方法模拟粒子在患者体内的输运径迹和相互作用,能够仿真放射源在体内的非均匀分布,还能以分子影像技术数据为输入,实现有关解剖几何、组织密度和异质性的个体化计算。Bozkurt等[42]对35例HCC患者分别进行基于直接蒙特卡罗和MIRD方法的剂量计算,根据LSF和摄入比分配源项在肿瘤、肝脏和肺部中的抽样比例。由于组织结构的个体化差异等原因,MIRD方法计算所得肿瘤组织、肝脏及肺部的吸收剂量,分别平均高估20%、5%、11%。MCs还提供了周围器官组织的剂量,例如,在这项研究中胆囊的平均剂量高达1.8 Gy。这一剂量差异与Abdul Hadi等[43]研究表现一致,后者根据患者99Tcm-MAA的SPECT影像定义源分布,MIRD法对肿瘤和正常肝脏实质吸收剂量分别高估20.23%和105.55%,而肺部剂量低估25.32%。上述报道充分说明,源项空间分布的异质性是引发剂量估算偏差的关键因素,以肿瘤形状尺寸和相对位置为代表的个体解剖学差异也会产生不同程度的影响。
MCs中高精度复杂几何仿真的统计准度低问题一般通过提高模拟粒子数解决,但需要消耗大量计算资源和时间,限制了该方法在常规临床的应用。为缩短计算耗时,减方差技术、仿真参数优化策略以及基于GPU的快速蒙特卡罗等方法被广泛研究。常用的蒙特卡罗仿真程序通常提供次级粒子阈值、能量截断、重要性与偏倚抽样等减方差技术。Cordeiro等[44]比较了GATE软件中5种减方差技术应用于体素体模器官S值的仿真效率,最高可提升62.5倍。在计算结果不确定度<10%的条件下,次级粒子阈值和分割指数径迹长度估计器组合的减方差技术可将计算耗时减小193~1 426倍。然而不确定度<5%或1%时,耗时优化程度显著下降的同时计算结果也产生偏差,这项技术对用户关于粒子输运过程的理解要求极高。Pistone等[45]通过组合多种分辨率和截断能量,研究以优化仿真参数提升准度和效率,结果表明体素体积增加8倍、次级粒子截断射程0.1~0.5 mm时,能确保与原始分辨率所得剂量差异<1%且计算时间减少55%左右,但GATE软件仍需约60 h的计算时间。此外,该研究样本容量较小,优化效果或受个体差异影响。基于CPU计算的蒙特卡罗输运程序的效率不能满足临床需求,Hissoiny等[46]利用基于GPU硬件层次模型和编程模型,重构现有的蒙特卡罗程序框架,实现异构快速蒙特卡罗程序加速算法和硬件并行,将计算效率提升200~900倍,有效地解决了粒子输运仿真耗时过长的问题。近年来,众多研究者将基于GPU的快速蒙特卡罗技术应用于核医学剂量计算,其中不乏应用于内照射剂量计算的案例[47-48],但目前尚未见其用于90Y-RE。
3. 体素S值:体素S值方法(voxel s-value,VSV)又被称为剂量体素核卷积(dose voxel kernel,DVK),由MIRD第17号手册提出[49]。VSV中每个体素被视为单独的源体素及相邻体素的靶体素,采用MCs计算体素S值(VSVs,特定核素和体素尺寸的剂量转换系数)和剂量核矩阵M,精确计算放射性源在每个体素内的能量转移和沉积情况。因计算代价小、速度快而被视作MCs的高效替代方案。VSVs的计算通常假设点源位于无限均匀的软组织或水介质中,这种基于单一材料的VSV又被称为单S值法(SSV),但因未考虑组织器官的异质性,常在与水密度差异较大的组织或组织交界处引入误差。在Capotosti等[50]关于VSV与MCs的研究中,两种方法在肝肺边界剂量差异约60%,肺部剂量差异更是高达-56%~70%。为优化组织非均匀问题,体素密度校正以及基于神经网络的VSVs数据库计算等策略被深入研究[51-52]。
(1) 密度校正VSVs:组合S值法(MSV)通过计算肺、软组织两种密度下的卷积核,对肺部和肝脏分别卷积。Plachouris等[53]估算了25例患者肝肺及其交界处剂量,单例VSV方法估算耗时<1 min。以MCs为金标准,肿瘤与健康肝实质的剂量估算偏差均 < 2%,而肺部器官剂量相对偏差高达10.16%,这可能由于肺部剂量因肺密度较低,β射线射程长而沉积少,直接蒙特卡罗所得剂量的统计不确定度较高。此外,肝、肺边界组织密度的非均匀也可能是偏差诱因之一。
为改善肝、肺边界的组织非均匀问题,卷积核中心归一化[54]和体素密度校正[55]等优化方法被提出,如公式(2)和(3):
| $ K_x^C=K_x \frac{\rho_x}{\rho_{\text {centervoxel }}} $ | (2) |
| $ K_x^D(i, j, k)=K_x(i, j, k) \frac{\rho_x}{\rho_{(i, j, k)}} $ | (3) |
式中,K为未经校正的单密度组织卷积核;x为肝脏或肺脏;ρ(i,j,k)为卷积核中位于(i,j,k)的体素密度。治疗后患者肝肺总剂量D用公式(4)可得:
| $ D=K_{ {liver }}^T \otimes \bar{A}_{ {liver }}+K_{ {lung }}^T \otimes \bar{A}_{ {lung }} $ | (4) |
式中,角标T代表未经校正、中心归一化C和体素密度校正D后的卷积核K,A为器官累积活度。Chen等[56-57]评价了10种组合密度校正方法的剂量估算效果。平均计算耗时均<30 s,较直接蒙特卡罗方法,肝脏、肿瘤剂量的相对标准偏差中位数 < 3%;未采用肺部密度校正时,肺剂量相对偏差>20%;采用任一肺部密度校正,肺剂量相对偏差中位数约为7%。但未见可兼顾肝、肺及器官交界处剂量准确度的组合。
(2) 神经网络方法:计算多种介质组合下的S值,可以直接解决组织非均匀问题,但需要消耗大量计算资源与时间。为提升计算效率,Akhavanallaf等[52]用体密度分布和蒙特卡罗所得S值作为训练集输入,用深度神经网络预测个体化体素模型中每个体素的S值,与18F-FDG活度分布图像卷积得到体剂量分布。每例全身体剂量分布的预测与卷积总耗时约为0.8 h,慢于MSV但仅为直接蒙特卡罗的千分之一。较直接蒙特卡罗方法,器官剂量的平均相对偏差低至2.6%,但尚未见此方法用于RE治疗。
4. 局部沉积法:局部沉积法(local deposition method,LDM;也称local energy deposition,LED)假设核素衰变的所有能量均沉积在源体素中,用体素内累积活度与每次衰变在源体素中产生的剂量因子Svoxel乘积计算单个体素吸收剂量。该方法尤其适合射程较短的α和β粒子,流程简易且计算迅速。在一项针对PM、LDM和经密度校正VSV方法的比较中,LDM所得肿瘤与健康肝实质剂量相对偏差仅为2.59%和0.97%,与PM方法相近,略高于VSV方法[57],与D′Arienzo等[58]的研究表现一致。
未考虑交叉火力效应是LDM方法不能确保RE治疗吸收剂量准确转换的重要因素。90Y衰变释放的β粒子在普通软组织和肺部的最大射程分别为11和44 mm,易在体素级别尤其在肺部及异质器官交界附近引入误差。同样在Chen等[57]对多种方法的比较中指出,LDM计算的肺部剂量差异为(18.48±7.75)%,与MCs的剂量差异大于PM和VSV计算所得,这或将增加术前LSF安全评估的风险。Pham等[59]试图用经肺密度校正的剂量转换因子改善肺部剂量估算准确度,但仍然存在约15%的剂量低估,剂量体积直方图的归一化均方根误差为0.41~0.45。未从根本解决交叉火力效应所致误差,此外,肿瘤的相对位置或也会影响剂量的偏差水平。
5. 剂量点卷积法:剂量点卷积法(dose point kernel,DPK)原理与VSV相似:蒙特卡罗计算单位活度点源在单一无限均匀介质中的剂量分布函数,对ROI进行空间离散化,根据时间积分活度分布卷积计算每个小体积元中的剂量[60]。Knešaurek[61]比较了LDM和DPK计算25例患者的全肝剂量,结果表现出较高的等效性[(53.59±23.47)Gy,(55.33±24.80)Gy]。但DPK同样存在组织非均匀问题,为此Scarinci等[62]训练了基于回归链、岭回归和弹性网络等3种机器学习模型,以材料密度分布及能谱为输入预测β放射性核素的sDPK,用于患者全肝和5个ROI的剂量估计。预测所得卷积核与Botta等[63]、Shiiba等[64]计算结果的相对偏差 < 10%,器官剂量较MCs低估约6%,计算时间从40 h缩短至7 min。对任意材料sDPK的快速预测能力,使其初步具备解决组织非均匀问题的潜力。
6. 神经网络:近年来,神经网络被广泛地应用于医学物理领域,在核医学内照射剂量计算中得到了初步应用和发展。Götz等[65]使用经验模态分解(empirical mode decomposition,EMD)所得密度图和MIRD方法计算的剂量分布训练U-Net深度神经网络,实现输入活度分布和CT图像后,对体剂量分布的预测。全身器官剂量预测耗时仅1.3 s,但EMD处理CT图像需1.9 h。以左肾为例,26例患者器官剂量较MCs的相对偏差为(-3.7±4.4)%,与Lee等[66]研究结果一致。后者采用10例MCs算得体剂量分布与PET/CT图像训练卷积神经网络(convolutional neural network,CNN),预测8个主要器官剂量的误差均值为(1.09± 1.09)%,而VSV与单房室模型法的误差均值分别为(8.47±1.35)%和(200.66±185.0)%,计算在0.06 h内完成。
个体化剂量计算的准确度不仅取决于粒子输运过程的重建精度,活度分布的准确性也是关键因素。在90Y轫致辐射SPECT成像中,高能光子的穿透和散射降低图像分辨率、引起伪影,降低剂量评估准度。为此,Jia等[67]创新性地提出了一种基于深度学习的框架,利用CNN进行散射校正并重建SPECT图像,随后训练残差网络来预测三维体剂量率分布。该方法通过模拟生成的虚拟患者的SPECT投影进行训练和测试,显著提高了剂量估算的准确度。与直接蒙特卡罗方法相比,病灶剂量率的归一化平均偏差分别达到了(8.6±5.7)%和(24.0±6.1)%,显示出超越传统“金标准”的潜力。这种表现或归因于残差网络在一定程度上纠正了前序处理中CNN引入的误差。尽管基于神经网络的剂量预测需要大量数据集进行训练且缺乏规范化的共识性文件,在临床中尚未得到推广,但它提供了一种高效、准确估算放射性治疗剂量的新途径。
7. 小结:在90Y放射性栓塞治疗中,选择合适的剂量计算方法对于确保治疗的疗效和安全性极为关键。上述方法应用于RE治疗的计算特性如表 1所示。MIRD方法因计算简便而广泛应用,但存在对肿瘤靶区剂量估计不足的风险。直接蒙特卡罗模拟作为“金标准”,精确模拟例子输运过程与源项分布,但计算资源和时间消耗大。体素S值法提供了快速计算的替代方案,但需考虑组织异质性的影响。局部沉积法适用于短射程粒子,计算迅速但可能引入交叉剂量误差。剂量点卷积法与体素S值法等效性高,但同样面临组织非均匀性问题。神经网络方法展现出高效准确的预测潜力,但需要大量数据训练且尚未广泛临床应用。各种方法均有其优势与局限,选择合适的剂量计算方法需综合考虑治疗需求、计算资源和准确性要求。
|
|
表 1 剂量估算方法特征概述 Table 1 The overview of dosimetric method characteristics |
为满足临床的精准和快速计算需求,用于90Y-RE治疗剂量的软件工具正迅速发展,可以分为器官级与体素级计算。器官级剂量计算软件,如OLINDA/EXM、Organ DosimetryTM和MIRDcalc等[68-69],多采用MIRD法以及标准参考人数据。支持用户选择放射性核素与体模类型,输出目标器官的平均吸收剂量。体素级软件以SPECT或PET图像作为源项分布的输入文件,配备自动分割或手动勾画功能,采用LDM(Hybrid3DTM SIRT、Planet® Dose等)或VSV(SurePlanTM LiverY90等)输出三维体剂量分布和剂量-体积直方图(DVHs)。尽管目前并非所有软件包都已在临床常规中使用,但它们在研究和开发个体化剂量学方法方面发挥着重要作用。
四、总结与展望90Y微球局部沉积栓塞的动力学特征简化了临床数据采集与剂量计算的流程,是内照射治疗中推广发展剂量学个体化、精细化和快速评估的理想对象。Garin等[70]在《柳叶刀·胃肠病学和肝病学》杂志发表的临床研究显示,个体化剂量学组患者的肿瘤平均吸收剂量提高约107.1 Gy,中位总生存期延长至26.6个月,总体反应率提升至50%,相较标准剂量学组的10.7个月和14%有显著改善。在治疗安全性方面,个体化剂量学组3级或以上不良事件发生率为57%,与标准治疗组的67%相近,不良反应风险并未显著增加。因此,在实施个体化剂量计划意义重大。MCs、VSV和LDM等三维体剂量估算方法为此提供了选择,基于GPU的快速蒙特卡罗方法和神经网络算法为核医学治疗剂量计划的快速制定提供了有力工具,利于缩小99Tcm-MAA与90Y栓塞的时间间隔,减少肝血管结构变化引起的剂量分布预测失准,降低患者治疗负担和医生工作负荷。
除剂量估算方法的准确性,引入更为精确的微球分布也有助于提升剂量预测的准确度。部分研究者通过应用计算流体动力学(computational fluid dynamics,CFD)技术,对90Y微球在肝血管中的分布特性进行了深入研究。研究表明,多种因素如血流动力学、导管类型、导管插入位置、肿瘤负荷以及微球的物理特性等[71-72],均能显著影响微球的分布。特别地,注射速度和导管位置被认为是影响分布的两个关键因素。Basciano等[73]发现在血管分叉附近注射时,5 mm的轴向位置变化可以使出口处微球分布的最大差异达到39.74%(10%肿瘤负担)。Bomberna等[74]的研究则显示,这一偏差的最大值仅为15%。微球最终在肿瘤外围的末端血管结构中以团簇形式沉积。Pasciak等[75]通过临床活检实验观察到,在微球数量密度较低时,团簇的分布呈现更大的不均匀性,导致肿瘤中接受较低吸收剂量的体积占比增加。相对地,在微球数量密度较高时,团簇分布虽然更为均匀,但可能增加对正常肝小叶造成毒性伤害的风险[76]。因此,深入研究90Y微球剂量的空间分布,不仅有助于为介入手术参数提供决策依据,还有望进一步提高治疗剂量、降低放射性并发症的发生率。尽管如此,当前研究仍存在计算时间长、模型简化、缺乏患者特定的血管动力学数据以及输入参数敏感性理解不足的局限性。此外,量化因素对剂量分布的具体影响,才能开发出精确控制这些参数的临床工具和方法。
发展和推广针对90Y微球放射性栓塞治疗的个体化快速剂量估算方法仍面临许多挑战。VSV、LDM和DVK法通过简化粒子输运流程提升了计算效率,但在计算复杂度降低的同时,无法完全捕获复杂几何和非均匀介质中的物理过程,在评估低密度器官及组织交界处的剂量时,仍然存有局限。新兴技术如快速蒙特卡罗模拟和神经网络有较高的技术门槛,后者尤其受制于训练数据集的获取难题。此外,90Y微球的分布预测普遍基于99Tcm-MAA的模拟结果,但其分布等效性尚存争议。除了估算方法对准确度的影响外,成像质量和分割效率也是确保精确和快速剂量估算的关键因素,有必要引入基于人工智能的自动分割技术以提升原始数据质量并缩短整体计划时间。在方法的推广方面,放射性栓塞治疗的剂量评估需依赖于影像医学、核医学和介入医学的紧密合作,这要求配套软件集成医学影像重建、自动分割与勾画,以及剂量计划等功能,研发难度较大。随着估算方法和放射生物模型的迅速更新,迫切需要在行业内达成共识,并推动剂量学计算方法和工具的标准化。
利益冲突 无
作者贡献声明 刘洪铭负责文献收集、数据整理、论文撰写与修改;邱睿、李君利指导论文修改
| [1] |
Ferlay J, Soerjomataram I, Dikshit R, et al. Cancer incidence and mortality worldwide: sources, methods and major patterns in GLOBOCAN 2012[J]. Int J Cancer, 2015, 136(5): E359-386. DOI:10.1002/ijc.29210 |
| [2] |
Chen W, Zheng R, Baade PD, et al. Cancer statistics in China, 2015[J]. CA Cancer J Clin, 2016, 66(2): 115-132. DOI:10.3322/caac.21338 |
| [3] |
牛娜, 林岩松. 90Y微球选择性内放射治疗在肝细胞癌中的应用及研究进展[J]. 中国癌症杂志, 2021, 31(5): 428-434. Niu N, Lin YS. Application and research progress of 90Y microspheres internal radiation therapy in colorectal cancer with liver metastasis[J]. Chin Oncol, 2021, 31(5): 428-434. DOI:10.19401/j.cnki.1007-3639.2021.05.009 |
| [4] |
刘书勋, 王嘉倍, 刘连新. 钇-90微球选择性放疗栓塞在肝癌治疗中的应用[J]. 中国现代普通外科进展, 2019, 22(7): 540-542, 582. Liu SX, Wang JB, Liu LX. Application of yttrium-90 microsphere selective internal radiation therapy embolization in the treatment of liver cancer[J]. Chin J Curr Adv Gen Surg, 2019, 22(7): 540-542, 582. DOI:10.3969/j.issn.1009-9905.2019.07.010 |
| [5] |
吴书其, 李超, 冯方, 等. 原发性肝癌和肝转移瘤的治疗: 第一部分——核医学技术[J]. 中华核医学与分子影像杂志, 2021, 41(10): 635-640. Wu SQ, Li C, Feng F, et al. Treatment of liver tumor and liver metastases, part 1: nuclear medicine techniques[J]. Chin J Nucl Med Mol Imaging, 2021, 41(10): 635-640. DOI:10.3760/cma.j.cn321828-20210902-00308 |
| [6] |
郑致远, 颜志平. 钇-90放射性微球治疗肝脏恶性肿瘤的应用进展[J]. 复旦学报(医学), 2020, 47(4): 622-627. Zheng ZY, Yan ZP. Application progress of yttrium-90 radiation microspheres in treatment of liver malignancies[J]. Fudan Univ J Med Sci, 2020, 47(4): 622-627. DOI:10.3969/j.issn.1672-8467.2020.04.025 |
| [7] |
耿建华, 陈英茂, 王晓涛, 等. 钇[90Y]树脂微球介入治疗的放射防护评估[J]. 中国辐射卫生, 2021, 30(6): 720-726. Geng JH, Chen YM, Wang XT, et al. Radiation protection assessment for interventional therapy with 90Y resin microspheres[J]. Chin J Radiol Health, 2021, 30(6): 720-726. DOI:10.13491/j.issn.1004-714X.2021.06.012 |
| [8] |
Kennedy A, Nag S, Salem R, et al. Recommendations for radioembolization of hepatic malignancies using yttrium-90 microsphere brachytherapy: a consensus panel report from the radioembolization brachytherapy oncology consortium[J]. Int J Radiat Oncol Biol Phys, 2007, 68(1): 13-23. DOI:10.1016/j.ijrobp.2006.11.060 |
| [9] |
Giammarile F, Bodei L, Chiesa C, et al. EANM procedure guideline for the treatment of liver cancer and liver metastases with intra-arterial radioactive compounds[J]. Eur J Nucl Med Mol Imaging, 2011, 38(7): 1393-1406. DOI:10.1007/s00259-011-1812-2 |
| [10] |
Busse NC, Al-Ghazi M, Abi-Jaoudeh N, et al. AAPM medical physics practice guideline 14. a: Yttrium-90 microsphere radioembolization[J]. J Appl Clin Med Phys, 2024, 25(2): e14157. DOI:10.1002/acm2.14157 |
| [11] |
中国医师协会介入医师分会临床诊疗指南专委会, 中国研究型医院学会肝胆胰外科专业委员会. 钇-90微球选择性内放射治疗肝脏恶性肿瘤规范化操作专家共识(2024版)[J]. 中华医学杂志, 2024, 104(7): 486-498. Chinese Medical Doctor Association, Clinical Guidelines Committee of Chinese College of Interventionalists, Chinese Research Hospital Association, Society for Hepato-pancreato-biliary Surgery. Expert consensus on the standardized procedure of selective internal radiation therapy with Yttrium-90 microspheres for liver malignancies (2024 edition)[J]. Natl Med J China, 2024, 104(7): 486-498. DOI:10.3760/cma.j.cn112137-20231025-00894 |
| [12] |
中国临床肿瘤学会核医学专家委员会, 北京市核医学质量控制和改进中心. 钇-90(90Y)微球选择性内放射治疗原发性和转移性肝癌的中国专家共识[J]. 中华肝脏病杂志, 2021, 29(7): 648-658. Nuclear Medicine Committee, Chinese Society of Clinical Oncology, Beijing Nuclear Medicine Quality Control and Improvement Center. Chinese expert consensus on selective internal radiation therapy with yttrium-90 for primary and metastatic hepatocellular carcinoma[J]. Chin J Hepatol, 2021, 29(7): 648-658. DOI:10.3760/cma.j.cn501113-20210302-00103 |
| [13] |
Weber M, Lam M, Chiesa C, et al. EANM procedure guideline for the treatment of liver cancer and liver metastases with intra-arterial radioactive compounds[J]. Eur J Nucl Med Mol Imaging, 2022, 49(5): 1682-1699. DOI:10.1007/s00259-021-05600-z |
| [14] |
Liu DM, Leung TW, Chow PK, et al. Clinical consensus statement: Selective internal radiation therapy with yttrium 90 resin microspheres for hepatocellular carcinoma in Asia[J]. Int J Surg, 2022, 102: 106094. DOI:10.1016/j.ijsu.2021.106094 |
| [15] |
Saini A, Wallace A, Alzubaidi S, et al. History and evolution of Yttrium-90 radioembolization for hepatocellular carcinoma[J]. J Clin Med, 2019, 8(1): 55. DOI:10.3390/jcm8010055 |
| [16] |
王斯妮, 贾中芝, 胡红杰, 等. 钇-90微球的特性、放射栓塞的操作技术及安全防护——钇-90微球放射栓塞系列回顾(一)[J]. 介入放射学杂志, 2017, 26(10): 952-958. Wang SN, Jia ZZ, Hu HJ, et al. Characteristics of yttrium- 90 microsphere, techniques and radiation safety of radioembolization procedure. A series review of radioembolization with yttrium-90 microspheres(partⅠ)[J]. J Intervent Radiol, 2017, 26(10): 952-958. DOI:10.3969/j.issn.1008-794X.2017.10.022 |
| [17] |
练德幸, 寇珊珊, 陆见霏, 等. 90Y树脂微球选择性内放射治疗放射防护检测与剂量评估[J]. 中华放射医学与防护杂志, 2022, 42(5): 385-390. Lian DX, Kou SS, Lu JF, et al. Radiological protection detection and dose assessment of selective internal radiotherapy with 90Y resin microspheres[J]. Chin J Radiol Med Port, 2022, 42(5): 385-390. DOI:10.3760/cma.j.cn112271-20220223-00066 |
| [18] |
Nijsen JF, van het Schip AD, Hennink WE, et al. Advances in nuclear oncology: microspheres for internal radionuclide therapy of liver tumours[J]. Curr Med Chem, 2002, 9(1): 73-82. DOI:10.2174/0929867023371454 |
| [19] |
Kim SP, Cohalan C, Kopek N, et al. A guide to 90Y radioembolization and its dosimetry[J]. Phys Med, 2019, 68: 132-145. DOI:10.1016/j.ejmp.2019.09.236 |
| [20] |
Vollmar B, Menger MD. The hepatic microcirculation: mechanistic contributions and therapeutic targets in liver injury and repair[J]. Physiol Rev, 2009, 89(4): 1269-1339. DOI:10.1152/physrev.00027.2008 |
| [21] |
贾中芝, 赵添, 王斯妮, 等. 钇-90微球放射栓塞治疗肝脏恶性肿瘤患者的术前评估与术后随访———钇-90微球放射栓塞系列回顾(二)[J]. 介入放射学杂志, 2017, 26(11): 1057-1062. Jia ZZ, Zhao T, Wang SN, et al. Series review of radioembolization with yttrium-90 microspheres (Part Ⅱ): pre-treatment evaluation and post-treatment follow-up for patients with hepatic malignancy receiving yttrium-90 microspheres embolization[J]. J Intervent Radiol, 2017, 26(11): 1057-1062. DOI:10.3969/j.issn.1008-794X.2017.11.022 |
| [22] |
Ertreo M, Choi H, Field D, et al. Comparison of cone-beam tomography and cross-sectional imaging for volumetric and dosimetric calculations in resin Yttrium-90 radioembolization[J]. Cardiovasc Intervent Radiol, 2018, 41(12): 1857-1866. DOI:10.1007/s00270-018-2030-0 |
| [23] |
Roncali E, Taebi A, Foster C, et al. Personalized dosimetry for liver cancer Y-90 radioembolization using computational fluid dynamics and monte carlo simulation[J]. Ann Biomed Eng, 2020, 48(5): 1499-1510. DOI:10.1007/s10439-020-02469-1 |
| [24] |
Garin E, Rolland Y, Laffont S, et al. Clinical impact of 99mTc-MAA SPECT/CT-based dosimetry in the radioembolization of liver malignancies with 90Y-loaded microspheres[J]. Eur J Nucl Med Mol Imaging, 2016, 43(3): 559-575. DOI:10.1007/s00259-015-3157-8 |
| [25] |
Garin E, Guiu B, Edeline J, et al. Trans-arterial radioembolization dosimetry in 2022[J]. Cardiovasc Intervent Radiol, 2022, 45(11): 1608-1621. DOI:10.1007/s00270-022-03215-x |
| [26] |
O'Doherty J. A review of 3D image-based dosimetry, technical considerations and emerging perspectives in 90Y microsphere therapy[J]. J Diagn Imaging Ther, 2015, 2(2): 1-34. DOI:10.17229/jdit.2015-0428-016 |
| [27] |
Walrand S, Hesse M, Jamar F, et al. A hepatic dose-toxicity model opening the way toward individualized radioembolization planning[J]. J Nucl Med, 2014, 55(8): 1317-1322. DOI:10.2967/jnumed.113.135301 |
| [28] |
Toskich BB, Liu DM. 90Y radioembolization dosimetry: concepts for the interventional radiologist[J]. Tech Vasc Interv Radiol, 2019, 22(2): 100-111. DOI:10.1053/j.tvir.2019.02.011 |
| [29] |
Li T, Ao ECI, Lambert B, et al. Quantitative imaging for targeted radionuclide therapy dosimetry - technical review[J]. Theranostics, 2017, 7(18): 4551-4565. DOI:10.7150/thno.19782 |
| [30] |
Van Audenhanege K, Van Holen R, Vandenberghe S, et al. Review of SPECT collimator selection, optimization, and fabrication for clinical and preclinical imaging[J]. Med Phys, 2015, 42(8): 4796-4813. DOI:10.1118/1.4927061 |
| [31] |
Snyder WS, Ford MR, Warner GG, et al. "S" absorbed dose per unit cumulated activity for selected radionuclides and organs[M]. New York: Society of Nuclear Medicine, 1975.
|
| [32] |
Sarwar A, Kudla A, Weinstein JL, et al. Yttrium-90 radioembolization using MIRD dosimetry with resin microspheres[J]. Eur Radiol, 2021, 31(3): 1316-1324. DOI:10.1007/s00330-020-07231-8 |
| [33] |
Woerner AJ, Johnson GE. Advances in Y-90 radioembolization for the treatment of hepatocellular carcinoma[J]. Hepatoma Res, 2022, 8: 3. DOI:10.20517/2394-5079.2021.122 |
| [34] |
Lawhn-Heath C, Hope TA, Martinez J, et al. Dosimetry in radionuclide therapy: the clinical role of measuring radiation dose[J]. Lancet Oncol, 2022, 23(2): e75-e87. DOI:10.1016/S1470-2045(21)00657-4 |
| [35] |
Yildirim OM, Bingolbali A, Bozkurt A, et al. Monte Carlo calculations of critical organ doses in radioembolization therapy of primary liver tumors via 90Y microspheres[J]. Int J Radiat Res, 2023, 21(3): 353-360. DOI:10.61186/ijrr.21.3.353 |
| [36] |
Chow P, Gandhi M, Tan SB, et al. SIRveNIB: selective internal radiation therapy versus sorafenib in Asia-Pacific patients with hepatocellular carcinoma[J]. J Clin Oncol, 2018, 36(19): 1913-1921. DOI:10.1200/JCO.2017.76.0892 |
| [37] |
Vilgrain V, Pereira H, Assenat E, et al. Efficacy and safety of selective internal radiotherapy with yttrium-90 resin microspheres compared with sorafenib in locally advanced and inoperable hepatocellular carcinoma (SARAH): an open-label randomised controlled phase 3 trial[J]. Lancet Oncol, 2017, 18(12): 1624-1636. DOI:10.1016/S1470-2045(17)30683-6 |
| [38] |
Gnesin S, Canetti L, Adib S, et al. Partition model-based 99mTc-MAA SPECT/CT predictive dosimetry compared with 90Y TOFPET/CT posttreatment dosimetry in radioembolization of hepatocellular carcinoma: a quantitative agreement comparison[J]. J Nucl Med, 2016, 57(11): 1672-1678. DOI:10.2967/jnumed.116.173104 |
| [39] |
Webster LA, Villalobos A, Majdalany BS, et al. Standard radiation dosimetry models: what interventional radiologists need to know[J]. Semin Intervent Radiol, 2021, 38(4): 405-411. DOI:10.1055/s-0041-1732323 |
| [40] |
Thomas MA, Mahvash A, Abdelsalam M, et al. Planning dosimetry for 90Y radioembolization with glass microspheres: Evaluating the fidelity of 99mTc-MAA and partition model predictions[J]. Med Phys, 2020, 47(10): 5333-5342. DOI:10.1002/mp.14452 |
| [41] |
Taebi A, Vu CT, Roncali E. Multiscale computational fluid dynamics modeling for personalized liver cancer radioembolization dosimetry[J]. J Biomech Eng, 2021, 143(1): 011002. DOI:10.1115/1.4047656 |
| [42] |
Bozkurt A, Toker GD, Erkilic M. A personalized Monte Carlo study of tumor and critical organ doses for trans-arterial radioembolization patients[J]. Phys Med Biol, 2023, 68(19): 195016. DOI:10.1088/1361-6560/acf7a7 |
| [43] |
Abdul Hadi M, Abdullah AN, Hashikin N, et al. Utilizing 3D Slicer to incorporate tomographic images into GATE Monte Carlo simulation for personalized dosimetry in yttrium-90 radioembolization[J]. Med Phys, 2022, 49(12): 7742-7753. DOI:10.1002/mp.15980 |
| [44] |
Cordeiro LP, de Sá LV, Kitamikado RA, et al. Optimized Monte Carlo simulations for voxel-based internal dosimetry[J]. Phys Med Biol, 2023, 68(11): 115004. DOI:10.1088/1361-6560/acd2a1 |
| [45] |
Pistone D, Italiano A, Auditore L, et al. GATE Monte Carlo dosimetry in 90Y TARE planning: influence of simulation parameters and image resampling on dosimetric accuracy and optimization of computational times[J]. Atti Accad Pelorit Pericol, 2021, 99(2): A4. DOI:10.1478/AAPP.992A4 |
| [46] |
Hissoiny S, Ozell B, Bouchard H, et al. GPUMCD: A new GPU-oriented Monte Carlo dose calculation platform[J]. Med Phys, 2011, 38(2): 754-764. DOI:10.1118/1.3539725 |
| [47] |
Peng Z, Lu Y, Xu Y, et al. Development of a GPU-accelerated Monte Carlo dose calculation module for nuclear medicine, ARCHER-NM: demonstration for a PET/CT imaging procedure[J]. Phys Med Biol, 2022, 67(6): 6N. DOI:10.1088/1361-6560/ac58dd |
| [48] |
Maneval D, Ozell B, Després P. pGPUMCD: an efficient GPU-based Monte Carlo code for accurate proton dose calculations[J]. Phys Med Biol, 2019, 64(8): 085018. DOI:10.1088/1361-6560/ab0db5 |
| [49] |
Bolch WE, Bouchet LG, Robertson JS, et al. MIRD pamphlet No. 17: The dosimetry of nonuniform activity distributions - Radionuclide S values at the voxel level[J]. J Nucl Med, 1999, 40(1): 11S-36S. |
| [50] |
Capotosti A, Merotti R, Vaccaro M, et al. The role of lung density in the voxel-based dosimetry of 90Y-tare evaluated with the voxel s-value(VSV)method and fast Monte Carlo simulation[J]. Appl Sci, 2024, 14(3): 1019. DOI:10.3390/app14031019 |
| [51] |
Götz TI, Lang EW, Schmidkonz C, et al. Dose voxel kernel prediction with neural networks for radiation dose estimation[J]. Z Med Phys, 2021, 31(1): 23-36. DOI:10.1016/j.zemedi.2020.09.005 |
| [52] |
Akhavanallaf A, Shiri I, Arabi H, et al. Whole-body voxel-based internal dosimetry using deep learning[J]. Eur J Nucl Med Mol Imaging, 2021, 48(3): 670-682. DOI:10.1007/s00259-020-05013-4 |
| [53] |
Plachouris D, Mountris KA, Papadimitroulas P, et al. Clinical evaluation of a three-dimensional internal dosimetry technique for liver radioembolization with 90Y microspheres using dose voxel kernels[J]. Cancer Biother Radiopharm, 2021, 36(10): 809-819. DOI:10.1089/cbr.2020.4554 |
| [54] |
Dieudonné A, Hobbs RF, Lebtahi R, et al. Study of the impact of tissue density heterogeneities on 3-dimensional abdominal dosimetry: comparison between dose kernel convolution and direct Monte Carlo methods[J]. J Nucl Med, 2013, 54(2): 236-243. DOI:10.2967/jnumed.112.105825 |
| [55] |
Götz T, Schmidkonz C, Lang EW, et al. A comparison of methods for adapting dose-voxel-kernels to tissue inhomogeneities[J]. Phys Med Biol, 2019, 64(24): 245011. DOI:10.1088/1361-6560/ab5b81 |
| [56] |
Chen G, Lu Z, Chen Y, et al. Voxel-S-value methods adapted to heterogeneous media for quantitative Y-90 microsphere radioembolization dosimetry[J]. Z Med Phys, 2023, 33(1): 35-45. DOI:10.1016/j.zemedi.2022.11.003 |
| [57] |
Chen G, Lu Z, Jiang H, et al. Voxel-S-Value based 3D treatment planning methods for Y-90 microspheres radioembolization based on Tc-99m-macroaggregated albumin SPECT/CT[J]. Sci Rep, 2023, 13(1): 4020. DOI:10.1038/s41598-023-30824-4 |
| [58] |
D'Arienzo M, Pimpinella M, Capogni M, et al. Phantom validation of quantitative Y-90 PET/CT-based dosimetry in liver radioembolization[J]. EJNMMI Res, 2017, 7(1): 94. DOI:10.1186/s13550-017-0341-9 |
| [59] |
Pham TP, Presles B, Popoff R, et al. Pre-treatment dosimetry in 90Y-SIRT: Is it possible to optimise SPECT reconstruction parameters and calculation methods for accurate dosimetry?[J]. Phys Med, 2023, 115: 103145. DOI:10.1016/j.ejmp.2023.103145 |
| [60] |
Martinov MP, Opara C, Thomson RM, et al. Fast beta-emitter Monte Carlo simulations and full patient dose calculations of targeted radionuclide therapy: introducing egs_mird[J]. Med Phys, 2022, 49(9): 6137-6149. DOI:10.1002/mp.15786 |
| [61] |
Knešaurek K. Comparison of posttherapy 90Y positron emission tomography/computed tomography dosimetry methods in liver therapy with 90Y microspheres[J]. World J Nucl Med, 2020, 19(4): 359-365. DOI:10.4103/wjnm.WJNM_23_20 |
| [62] |
Scarinci I, Valente M, Pérez P. A machine learning-based model for a dose point kernel calculation[J]. EJNMMI Phys, 2023, 10(1): 41. DOI:10.1186/s40658-023-00560-9 |
| [63] |
Botta F, Mairani A, Battistoni G, et al. Calculation of electron and isotopes dose point kernels with FLUKA Monte Carlo code for dosimetry in nuclear medicine therapy[J]. Med Phys, 2011, 38(7): 3944-3954. DOI:10.1118/1.3586038 |
| [64] |
Shiiba T, Kuga N, Kuroiwa Y, et al. Evaluation of the accuracy of mono-energetic electron and beta-emitting isotope dose-point kernels using particle and heavy ion transport code system: PHITS[J]. Appl Radiat Isot, 2017, 128: 199-203. DOI:10.1016/j.apradiso.2017.07.028 |
| [65] |
Götz TI, Schmidkonz C, Chen S, et al. A deep learning approach to radiation dose estimation[J]. Phys Med Biol, 2020, 65(3): 035007. DOI:10.1088/1361-6560/ab65dc |
| [66] |
Lee MS, Hwang D, Kim JH, et al. Deep-dose: a voxel dose estimation method using deep convolutional neural network for personalized internal dosimetry[J]. Sci Rep, 2019, 9(1): 10308. DOI:10.1038/s41598-019-46620-y |
| [67] |
Jia Y, Li Z, Akhavanallaf A, et al. 90Y SPECT scatter estimation and voxel dosimetry in radioembolization using a unified deep learning framework[J]. EJNMMI Phys, 2023, 10(1): 82. DOI:10.1186/s40658-023-00598-9 |
| [68] |
Danieli R, Milano A, Gallo S, et al. Personalized dosimetry in targeted radiation therapy: a look to methods, tools and critical aspects[J]. J Pers Med, 2022, 12(2): 205. DOI:10.3390/jpm12020205 |
| [69] |
Stabin MG, Sparks RB, Crowe E. OLINDA/EXM: the second-generation personal computer software for internal dose assessment in nuclear medicine[J]. J Nucl Med, 2005, 46(6): 1023-1027. |
| [70] |
Garin E, Tselikas L, Guiu B, et al. Personalised versus standard dosimetry approach of selective internal radiation therapy in patients with locally advanced hepatocellular carcinoma (DOSISPHERE-01): a randomised, multicentre, open-label phase 2 trial[J]. Lancet Gastroenterol Hepatol, 2021, 6(1): 17-29. DOI:10.1016/S2468-1253(20)30290-9 |
| [71] |
Snoeijink TJ, Vlogman TG, Roosen J, et al. Transarterial radioembolization: a systematic review on gaining control over the parameters that influence microsphere distribution[J]. Drug Deliv, 2023, 30(1): 2226366. DOI:10.1080/10717544.2023.2226366 |
| [72] |
Aramburu J, Antón R, Rodríguez-Fraile M, et al. Computational fluid dynamics modeling of liver radioembolization: a review[J]. Cardiovasc Intervent Radiol, 2022, 45(1): 12-20. DOI:10.1007/s00270-021-02956-5 |
| [73] |
Basciano CA, Kleinstreuer C, Kennedy AS, et al. Computer modeling of controlled microsphere release and targeting in a representative hepatic artery system[J]. Ann Biomed Eng, 2010, 38(5): 1862-1879. DOI:10.1007/s10439-010-9955-z |
| [74] |
Bomberna T, Koudehi GA, Claerebout C, et al. Transarterial drug delivery for liver cancer: numerical simulations and experimental validation of particle distribution in patient-specific livers[J]. Expert Opin Drug Deliv, 2021, 18(3): 409-422. DOI:10.1080/17425247.2021.1853702 |
| [75] |
Pasciak AS, Bourgeois AC, Bradley YC, et al. A Microdosimetric analysis of absorbed dose to tumor as a function of number of microspheres per unit volume in 90Y radioembolization[J]. J Nucl Med, 2016, 57(7): 1020-1026. DOI:10.2967/jnumed.115.163444 |
| [76] |
Högberg J, Rizell M, Hultborn R, et al. Simulation model of microsphere distribution for selective internal radiation therapy agrees with observations[J]. Int J Radiat Oncol Biol Phys, 2016, 96(2): 414-421. DOI:10.1016/j.ijrobp.2016.05.007 |
 2024, Vol. 44
2024, Vol. 44
