2. 中国科学技术大学研究生院科学岛分院, 合肥 230026;
3. 安徽医科大学基础医学院核医学教研室, 合肥 230032
2. Science Island Branch, Graduate School of USTC, Hefei 230026, China;
3. Department of Nuclear Medicine, Basic Medical College, Anhui Medical University, Hefei 230032, China
质子放疗是一种新兴治疗技术,目前,临床治疗计划将质子的相对生物效能(relative biological effectiveness,RBE)取值为1.1,且相同的RBE值应用于肿瘤和正常组织,但据相关研究报道,质子的RBE值是可变的,并且RBE值与辐射类型、辐射能量以及不同的生物终点有关[1-2],DNA双链断裂产额(double-strand breaks yields,YDSBs)是其中最可靠的生物学终点之一[3-4]。秀丽隐杆线虫凭借着突变体资源丰富、不变的细胞谱系等优势成为研究DNA损伤修复的重要模式生物之一,研究表明,线虫是X、γ等射线辐照后的良好DNA损伤检测对象[5-6]。目前检测DNA双链断裂(double-strand breaks,DSB)的生物手段主要有彗星实验[7]、凝胶电泳技术[8]、γ-H2AX焦点计数法[9]、NGS测序分析[10]等。然而,上述生物学检测存在灵敏度低、操作流程复杂、成本高等问题。此外,与哺乳动物细胞相比,线虫DSB的检测在生殖细胞解剖、固定等方面的操作难度更高,而利用蒙特卡罗(Monte Carlo,MC)模拟进行辐射诱导YDSBs的计算,成为量化DSB的热点方法之一。其中Geant4-DNA可模拟电离辐射与DNA的相互作用过程,并可定量分析YDSBs[11-13],但在Geant4-DNA中,以辐射诱导的DSB总产额为生物终点,计算质子RBE的相关研究还较少。
本研究利用Geant4-DNA程序包模拟计算100、50、20、5和2 MeV的质子在不同模拟参数下诱导线虫生殖细胞的YDSBs,并与相关分子生物学检测结果进行对比验证;比较不同能量质子诱导DNA损伤类型的差异;以DSB总产额为生物终点计算质子的RBEDSB值,并将计算结果进行非线性拟合,获得质子的RBEDSB与能量之间的数学关系。
材料与方法 1、DNA模型的建立将线虫生殖细胞构建成直径为20 μm的球体,细胞核构建成半径为2.8 μm的球体,其介质都填充为“G4_Water”,细胞外的介质填充为“G4_Galactic”。线虫生殖细胞DNA模型则是根据Sakata等[14]提出的希尔伯特曲线方法进行构建,如图 1所示。在细胞核中,DNA链缠绕在组蛋白上,紧密地形成染色质纤维,组蛋白近似为球体。在边长250 nm的小立方体放置直链螺线管片段和弯链螺线管片段,其中直链螺线管片段包含24 400个碱基对和125个组蛋白,如图 1A所示,弯链螺线管片段包含17 193个碱基对和88个组蛋白,如图 1B所示。上述螺线管片段被放置在250 nm的小立方体中,以希尔伯特曲线的方式连接在一起,形成半径为2.8 μm的球状连续片段,填满整个细胞核。最终希尔伯特曲线经过6次迭代后,形成262 144个区域,使得球状细胞核内碱基对总数约为100 Mb,与线虫生物学基因组大小100.3 Mb相吻合[15]。

|
注:黄色、蓝色和绿色分别代表DNA、组蛋白和linker DNA 图 1 线虫生殖细胞DNA模型 A. 直链染色质片段;B. 弯链染色质片段 Figure 1 DNA model of a C. elegans germ cell A. Straight-chain chromatin segment; B. Bent-chain chromatin segment |
2、DNA直接损伤
为了模拟物理阶段的DNA损伤,Geant4-DNA提供了3组物理构造函数G4EmDNA Physics_option2 (构造函数2)、G4EmDNA Physics_option4 (构造函数4)和G4EmDNA Physics_option6 (构造函数6)[16-17]。在这些构造函数中,用于模拟液态水中电子相互作用的模型彼此不同,但模拟水中光子、质子以及重离子相互作用的模型一致。构造函数2可追踪的电子能量范围为7.4 eV~1 MeV,构造函数4可追踪的电子能量范围为10 eV~10 keV,而构造函数6追踪的电子能量范围为11 eV~256 keV。此外,在模拟水中电子相互作用过程中,与构造函数2相比,构造函数4的激发截面明显增强,电离截面略有减小;在整个能量范围内,构造函数6的电离截面高于构造函数2和4,而在20 eV电子能量以下的范围内,激发截面低于构造函数4[18]。对于直接损伤的模拟,需要确定能量沉积点到DNA链的距离(用R direct表示)以及能量阈值(用ET表示)模型两个参数,以此将DNA分子附近的能量沉积与DNA损伤联系起来。根据Sakata等[19]方法,将R direct设置为3.5 Å,对于ET模型,本研究采用8.22、10.79、12.6、17.5和21.25 eV的单能ET模型以及5~37.5 eV的线性比例模型。
3、DNA间接损伤间接损伤主要来源于射线与生物大分子周围的水反应,水分子被电离和激发后发生辐射分解反应产生自由基。当自由基扩散到DNA分子上发生化学反应时,就会对化学损伤进行评估。Sakata等[19]认为化学反应导致DNA链断裂主要发生在·OH自由基和糖-磷酸基团之间,并将该反应诱导SSB的概率POH设置为40.5%。此外,为了减少辐射分解模拟的计算时间,还需确定以下两个化学参数:①dkill,即距离DNA一定范围外的自由基都会被清除;②Tchem,即·OH自由基被杀死所需的时间。本研究采用以上参数,化学构造函数选用G4EmDNAchemistry_option3[20],并采用新开发的独立反应时间(IRT)[21]进行模拟。
4、DNA损伤分类为了明确DNA损伤的各种类型,本研究参考Nikjoo等[22]提出的分类标准,将DNA片段损伤进行分类。根据损伤的来源,分成直接损伤(SSBd和DSBd)、间接损伤(SSBin和DSBin)和混合损伤(SSBm、DSBm和DSBh)。根据损伤的复杂性,DNA链断裂分成简单单链断裂(SSB)、简单双链断裂(DSB)、复杂单链断裂(SSB+和2SSB)以及复杂双链断裂(DSB+和DSB++)。
5、模拟计算方法使用Geant4-DNA工具包(Geant4-v11.1.1)模拟质子对线虫生殖细胞的DNA损伤。质子辐照细胞模拟计算,质子源设置为半径2.8 μm的圆形面源,位置距离细胞上方3 μm,入射方向垂直细胞核。对于2 MeV能量的质子,模拟个数为2 000个;5~100 MeV能量的质子,模拟的个数约为104个,使得不同能量的质子辐照细胞时,剂量约为102 Gy,每次计算结果的相对标准偏差在1%以下,这些偏差在可接受范围内, 保证了模拟的可信度。误差计算公式见公式(1):
| $ \text { RSD }=\frac{S D_{-} \text {yields }}{\text { yields }} \times 100 \% $ | (1) |
式中,SD_yields为辐射诱导的SSB产额或DSB产额标准差,(Gy·Mbp)-1;yields为辐射诱导的SSB产额或DSB产额,(Gy·Mbp)-1;RSD为相对标准偏差。
6、DSB产额与DSB数目换算将生物学实验中质子诱导的线虫生殖细胞DSB数目进行换算,得到对应的DSB产额,如公式(2)所示:
| $ Y_{\mathrm{DSB}}=\frac{N_{\mathrm{DSB}}}{D \times N_{\mathrm{bp}}} $ | (2) |
式中,NDSB为DSB数目;YDSB为DSB产额,(Gy·Mbp)-1;D为吸收剂量,Gy;Nbp为线虫生殖细胞碱基对总数,Mbp,线虫生殖细胞碱基对总数约100.3 Mbp。
7、RBEDSB计算RBE是衡量不同电离辐射生物学效应的重要指标之一。本研究按照Zabihi等[23]和Pater等[24]的方法将RBEDSB定义为质子辐射诱导的线虫生殖细胞DSB产额与参考辐射60Co诱导的DSB产额之比,如公式(3)所示:
| $ \mathrm{RBE}_{\mathrm{DSB}}=\frac{Y_{\mathrm{DSB}} \mathrm{A}_{\text{质子}}}{Y_{\mathrm{DSB}^{60} \mathrm{Co}}} $ | (3) |
式中,YDSB质子为以DSB为生物学终点时,质子诱导的DSB产额,(Gy·Mbp)-1;YDSB60Co为以DSB为生物学终点时,60Co辐射同等剂量下诱导的DSB产额,(Gy·Mbp)-1。
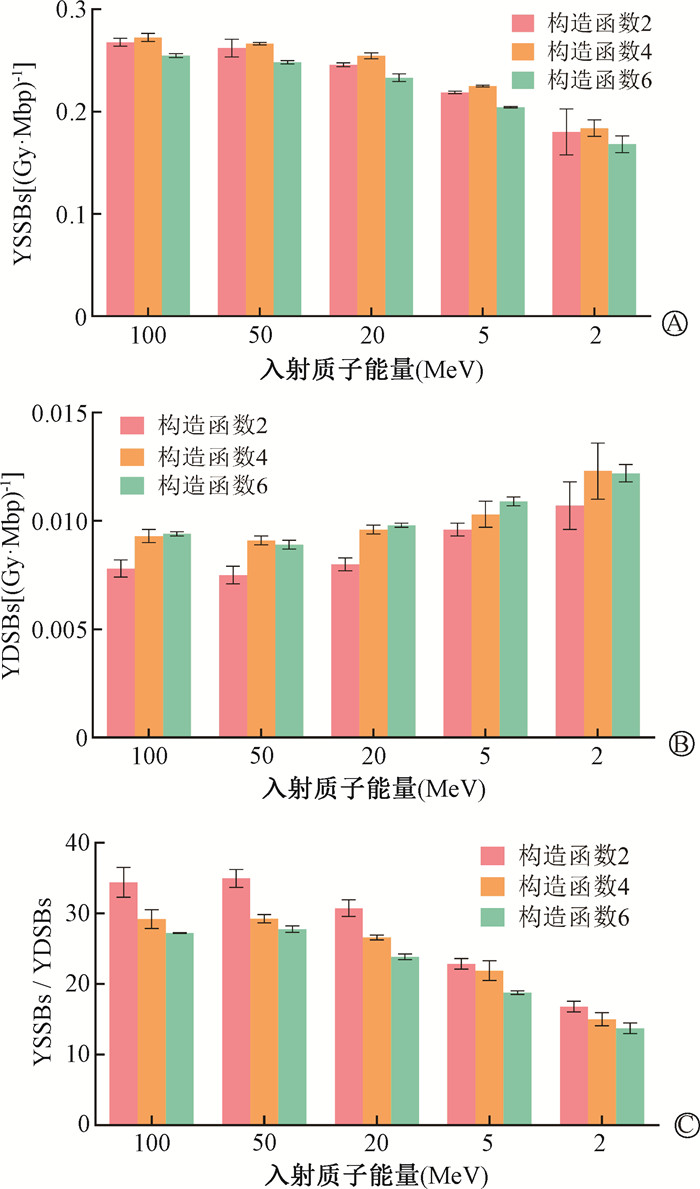
结果 1、物理构造函数与DNA损伤的关系不同物理构造函数下质子诱导线虫生殖细胞SSB产额(YSSBs)、DSB产额(YDSBs)以及YSSBs/YDSBs比值如图 2。由图 2A可知,当选取构造函数6时,质子诱导的YSSBs最低,构造函数4和构造函数2诱导的YSSBs相差不大,构造函数4诱导的YSSBs略高于构造函数2;由图 2B可知,当选取构造函数2时,质子诱导的YDSBs最低,构造函数4和构造函数6诱导的YDSBs相差不大。由图 2C可知,3种构造函数下YSSBs/YDSBs的比值从高到低依次为构造函数2、构造函数4和构造函数6。
|
注:YSSBs. 单链断裂总产额;YDSBs. 双链断裂总产额 图 2 不同构造函数与线虫生殖细胞DNA损伤的关系 A. SSB产额;B. DSB产额;C. SSB/DSB产额的比值 Figure 2 Correlation between different physics constructors and DNA damage in C. elegans germ cells A. YSSB; B. YDSB; C. YSSB/YDSB ratio |
2、能量阈值模型与DNA损伤的相关性
在不同单能ET和线性ET模型下质子诱导线虫生殖细胞YSSBs、YDSBs和YSSBs/YDSBs比值如图 3。由图 3A可知,随着单能ET的增加,质子诱导的YSSBs在逐渐降低,线性ET模型的计算结果与17.5 eV的单能ET模型较为接近;此外,不同ET模型诱导的YSSBs都随着质子入射能量的降低而降低,且变化幅度较大,在20%以上。由图 3B可知,YDSBs随着单能ET的增加呈下降趋势,线性ET模型的计算结果也与17.5 eV的单能ET模型较为接近;随着质子能量的降低,不同ET模型诱导的YDSBs呈现与YSSBs相反的变化趋势,且变化较为平缓。由图 3C可知,质子诱导的YSSBs/YDSBs比值随着单能ET的增加而增加,线性ET模型的计算结果同样与17.5 eV的单能ET模型较为接近;不同ET模型计算的YSSBs/YDSBs比值随着质子入射能量的降低而降低。

|
注:YSSBs. 单链断裂总产额;YDSBs. 双链断裂总产额 图 3 不同ET模型与线虫生殖细胞DNA损伤的相关性 A. SSB产额;B. DSB产额;C. SSB/DSB产额的比值 Figure 3 Correlation between different ET models and DNA damage in C. elegans germ cells A. YSSB; B. YDSB; C. YSSB/YDSB ratio |
3、自由基清除距离对DNA损伤的影响
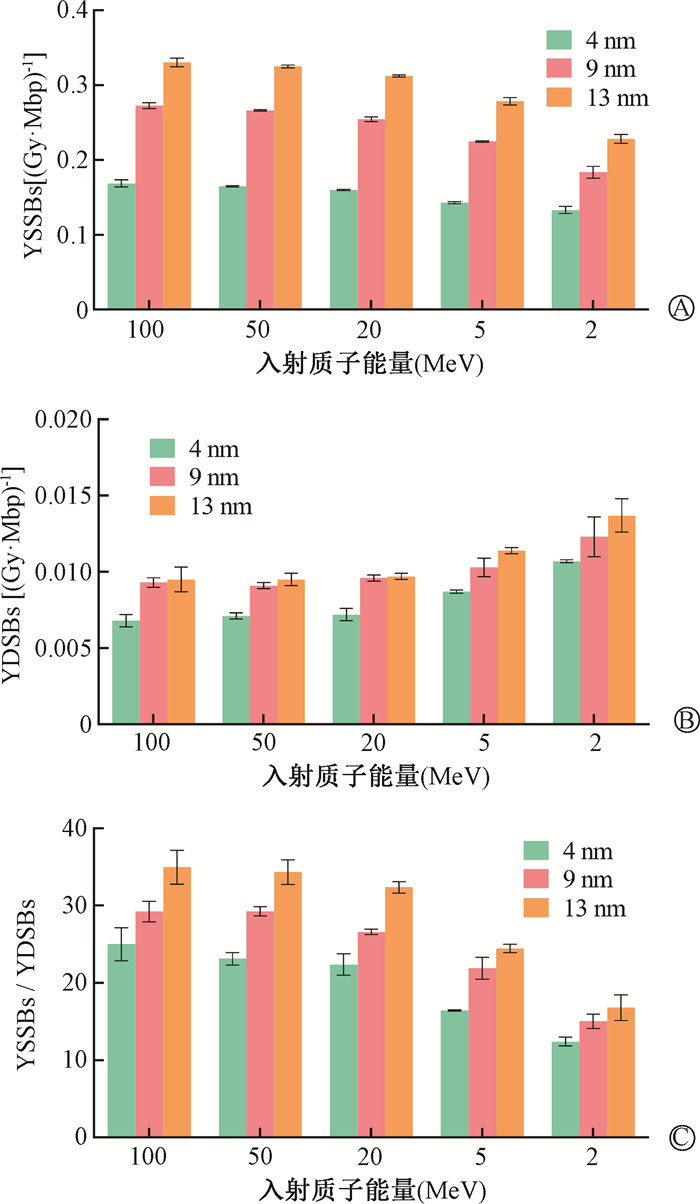
不同自由基清除距离对线虫生殖细胞YSSBs、YDSBs和YSSBs/YDSBs比值影响如图 4。当自由基清除距离设置越长时,化学阶段反应时间越长,质子诱导的YSSBs、YDSBs以及YSSBs/YDSBs都在增加,但增加的幅度变得缓慢,尤其是YSSBs和YDSBs。
|
注:YSSBs.单链断裂总产额;YDSBs.双链断裂总产额 图 4 不同自由基清除距离下质子对线虫生殖细胞DNA损伤的影响 A. SSB产额;B. DSB产额;C. SSB/DSB产额的比值 Figure 4 Impacts of proton irradiation on DNA damage in C. elegans germ cells at different free radical scavenging distances A. YSSB; B. YDSB; C. YSSB/YDSB ratio |
4、与生物实验数据对比及分析
本研究的模拟结果与Min等[25]实验结果进行对比,验证模拟的准确性并选取计算线虫DNA损伤的最佳模拟参数。Min等[25]用20 MeV的质子辐照线虫,辐照剂量为10 Gy时,通过免疫荧光标记RAD-51病灶数得出生殖细胞单个细胞核的DSB数目为(6.0 ± 1.75)个,经过公式(2)计算可得DSB产额约为0.006(Gy·Mbp)-1。因此,本研究模拟了同样剂量下20 MeV质子诱导的DSB产额,结果表明当选取构造函数4、21.25 eV的ET模型和9 nm的自由基清除距离时,DSB产额约为0.006 5(Gy·Mbp)-1,此时模拟结果与实验结果最为接近,两者相差约8.3%。
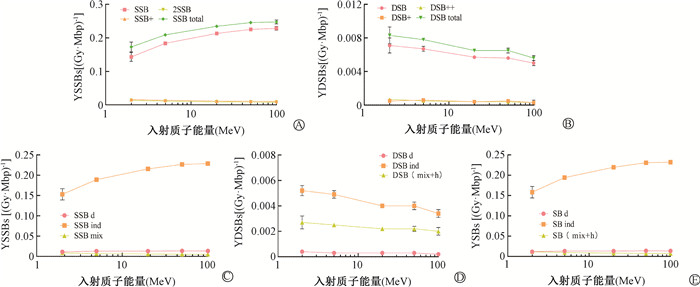
5、不同能量质子对DNA损伤类型的影响选取物理构造函数4、21.25 eV的ET模型和9 nm的自由基清除距离3个参数,研究不同能量质子诱导线虫生殖细胞DNA损伤类型。不同能量质子诱导DNA单双链断裂按照复杂性分类如图 5。当入射质子能量降低时,质子的传能线密度(linear energy transfer,LET)增加。由图 5A可知,在DNA单链断裂中,SSB总产额(SSB total)和SSB随着入射质子LET的增加而降低,SSB+和2SSB则随着LET的增加而增加,表明质子能量越低,其LET越高,SSB复杂损伤增多;由图 5B可知,在DNA双链断裂中,DSB总产额(DSB total)、DSB以及DSB++随着LET的增加而增加,而DSB+基本保持不变,表明高LET质子辐射更易引发难以修复的复杂DSB损伤。不同能量质子诱导DNA单双链断裂按照来源分类如图 5C~E所示,对于质子诱导的SSB和DSB来说,间接损伤都占主导地位;直接和间接损伤导致的SSB产额随LET的增加而降低,混合损伤导致的SSB随LET的增加而增加;SB产额(包括SSB和DSB损伤产额)变化趋势与SSB产额一致;对于DSB而言,间接和混合损伤导致的DSB产额随着LET的增加而增加,直接损伤几乎不变。
|
注:YSSBs.单链损伤产额;YDSBs.双链损伤产额 图 5 质子诱导线虫生殖细胞DNA损伤类型 A. SSB按照复杂性分类;B. DSB按照复杂性分类;C. SSB按照来源分类;D. DSB按照来源分类;E. SB按照来源分类 Figure 5 Types of proton irradiation -induced DNA damage in C. elegans germ cells A. Complexity-based categorization of SSB; B. Complexity-based categorization of DSB; C. Source-based categorization of SSB; D. Source-based categorization of DSB; E. Source-based categorization of SB |
6、质子的RBEDSB
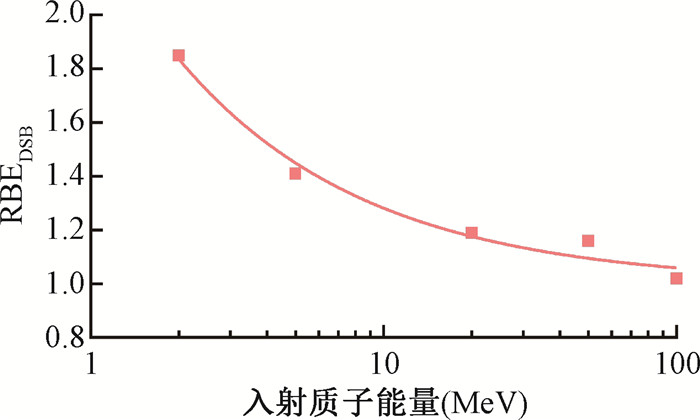
为探究不同能量质子的RBEDSB值,根据公式(3)计算了100、50、20、5和2 MeV质子的RBEDSB,并对计算结果进行非线性拟合,如图 6。60Co诱导的线虫生殖细胞DSB产额0.007 6(Gy·Mbp)-1,其模拟参数选择的是构造函数4、线性ET模型和9 nm的自由基清除距离,因此计算质子的RBEDSB时,也基于上述参数。拟合结果如公式(4)所示:
| $ \mathrm{RBE}_{\mathrm{DSB}}=1.34 \times E^{-0.68}+1\left(R^2=0.982\right) $ | (4) |
|
图 6 不同能量质子诱导线虫生殖细胞的RBEDSB Figure 6 RBEDSB of the C. elegans germ cell induced by proton iurradiation at varying energy levels |
式中,RBEDSB表示质子的RBE;E表示入射质子的能量,MeV。
如图 6所示,随着入射质子能量的降低,RBEDSB逐渐增加,表明低能质子对线虫生殖细胞辐射损伤危害程度更高;当能量不断增加时,质子的RBEDSB越来越接近1。
讨论在本研究中,利用Geant4-DNA分析了3种物理构造函数、能量阈值模型与自由基清除距离对线虫生殖细胞DNA损伤的影响。结果表明,模拟参数的差异会导致DNA损伤产额的较大差异。当选择构造函数6时,不同能量的质子诱导的YDSBs最多,这与Zhu等[26]计算的人体成纤维细胞以及Lampe等[27]计算的简单几何DNA模型结果一致,这主要是由于构造函数6具有更高的电离截面所致。然而,在研究物理构造函数对DNA损伤时,对于哪一类构造函数是正确的没有共识。在本研究中,绝大多数模拟采用了构造函数4,因为该构造函数反映了一种更精确的轨道径迹建模方法。不同能量的质子在不同单能ET模型下诱导的YSSBs和YDSBs变化趋势与Zhu等[26]计算结果一致,这表明随着单能ET的增加,大多数能量沉积事件发生概率降低。线性ET模型诱导的YDSBs略高于单能17.5 eV的计算结果,YSSBs/YDSBs相反,这与Zhu等[28]和Meylan等[29]计算的人体细胞结果一致。对于化学反应模拟参数而言,随着化学阶段反应时间的延长,会诱导更高的YSSBs和YDSBs,这与Zhu等[28]的结果一致,这主要是由于羟基自由基在被清除之前会扩散得更远,从而增加与DNA片段相互作用的概率,诱导更高的DNA损伤产额。
本研究将不同参数下的模拟结果与相关实验数据对比之后,结果表明,选取构造函数4、21.25 eV的ET模型和9 nm的自由基清除距离时两者最为接近。然而,本研究可参考的分子生物学实验结果极少, 因此这一结论仍需要更多的生物学实验数据来验证。为了比较不同能量质子的辐射生物效应,本文在上述模拟参数下进一步探究了质子诱导线虫生殖细胞DNA损伤类型,质子能量越低,诱导的DSB复杂损伤越多,这与王蕴楠[30]和唐菁[31]计算的质子诱导人体细胞DNA损伤结果一致。当质子能量较低时,其LET越大,质子辐射DNA时,能量沉积点越密集,导致在局部范围内同时产生多种DNA损伤类型,并最终复合形成复杂损伤,从而增加了DNA链损伤的复杂性。对比DNA损伤来源发现,间接损伤始终占主导地位,并且间接损伤导致的SB损伤产额随着质子能量的降低而降低,这与Sakata等[14]模拟的质子辐照人体细胞结果一致,这主要是因为在高LET下,入射质子迅速减速,导致能量沉积密集,该处产生许多辐解产物,在辐解产物密度高的情况下,化学物质相互作用而不是与DNA相互作用,导致间接损伤降低。
此外,本文以DSB总产额作为生物终点计算不同能量质子的RBEDSB值,计算结果表明RBEDSB在1.02和1.85之间变化,变化趋势与唐菁等[32]研究的质子辐照成纤维细胞结果一致,即质子能量越低,RBEDSB越高。不同的是,唐菁等[32]计算的分别是简单DSB断裂(RBEDSB)和复杂DSB断裂(RBEDSBC)的RBE值。Pater等[24]以及Shamshiri等[33]探究质子RBE时,虽然也是以DSB为生物终点,但仅计算了直接损伤诱导的DSB产额,进而表征质子的RBE。然而,在辐射诱导的DNA损伤中,间接损伤占主导地位,忽略间接损伤所诱导的DSB产额而计算的RBE值,考虑不够全面,因此以DSB总产额作为生物终点评估质子的辐射生物效应更具有指导意义。
目前,在临床放疗中,光子放疗技术日益成熟,虽然光子放疗能够保证肿瘤照射剂量,但肿瘤周围正常组织受到了更多的中、低剂量照射。质子放疗技术相较于传统的光子放疗,具有显著的精准定位优势,能够更精确地将治疗射线集中于肿瘤部位,从而在理论上减少放疗过程中对周围正常组织的照射。尽管完全避免对周围健康组织的影响存在挑战,质子放疗技术仍然在减少对正常组织的损伤方面显示出了其潜力。在本研究模拟中,入射质子能量计算上限为100 MeV, 而能量≥200 MeV的质子用于一般治疗过程[34],因此无法直接通过模拟得出200 MeV质子的RBEDSB,将能量为200 MeV的质子按照本研究拟合的公式(4)计算其RBEDSB,可得RBEDSB约为1.04,这与Mohan和Grosshans[35]的报道一致,即质子的RBE在布拉格峰入口区域接近1,这进一步证实了质子放疗在精确治疗肿瘤方面的潜力和优势。自20世纪60年代以来,辐射防护领域已经提出用辐射品质和辐射权重因子来表征不同种类的辐射对机体的危害程度,后来辐射权重因子逐渐取代了辐射品质。国际放射防护委员会(ICRP)第103号出版物曾建议将质子的辐射权重因子设定为2。这主要有以下3点原因:一是低能质子在人体组织中的射程很短,绝大多数被皮肤吸收;二是在实际应用场景中高能质子所占比例最高;三是大量实验数据表明质子辐射的RBE在1和2之间[36-37]。根据本研究结果表明,以DNA双链断裂产额作为生物终点,计算的质子RBE均未超过2,与上述结论一致。
综上所述,本研究建立了线虫生殖细胞DNA模型,比较了不同能量质子诱导的DNA损伤类型,并以DSB总产额为生物终点,建立了质子的相对生物效应值与其能量之间的数学关系,为表征不同能量质子的RBE提供了理论依据。此外,本文拓展了Geant4-DNA中已有的DNA模型,构建了更符合生物学实验数据的线虫生殖细胞DSB计算模型,为检测线虫DSB提供了新思路。
利益冲突 无
作者贡献声明 季涛涛负责研究实施和论文撰写及修改;徐照、李桃生负责指导研究方案和论文修改;余威悦负责论文修改和研究方案讨论
| [1] |
Jr DL, Wambersie A, Whitmore G. Prescribing, recording and reporting proton-beam therapy[J]. J ICRU, 2007, 7(2): 1-210. DOI:10.1093/jicru_ndm021 |
| [2] |
Paganetti H. Relative biological effectiveness (RBE) values for proton beam therapy. Variations as a function of biological endpoint, dose, and linear energy transfer[J]. Phys Med Biol, 2014, 59(22): R419-472. DOI:10.1088/0031-9155/59/22/R419 |
| [3] |
Nikjoo H, Emfietzoglou D, Liamsuwan T, et al. Radiation track, DNA damage and response-a review[J]. Rep Prog Phys, 2016, 79(11): 116601. DOI:10.1088/0034-4885/79/11/116601 |
| [4] |
Kyriakou I, Tremi I, Georgakilas AG, et al. Microdosimetric investigation of the radiation quality of low-medium energy electrons using Geant4-DNA[J]. Appl Radiat Isot, 2021, 172: 109654. DOI:10.1016/j.apradiso.2021.109654 |
| [5] |
Weidhaas JB, Eisenmann DM, Holub JM, et al. A Caenorhabditis elegans tissue model of radiation-induced reproductive cell death[J]. Proc Nati Acad Sci USA, 2006, 103(26): 9946-9951. DOI:10.1073/pnas.0603791103 |
| [6] |
Gartner A, Milstein S, Ahmed S, et al. A conserved checkpoint pathway mediates DNA damage-induced apoptosis and cell cycle arrest in C. elegans[J]. Mol Cell, 2000, 5(3): 435-443. DOI:10.1016/S1097-2765(00)80438-4 |
| [7] |
Olive Pl. Impact of the comet assay in radiobiology[J]. Mutat Res, 2009, 681(1): 13-23. DOI:10.1016/j.mrrev.2007.11.001 |
| [8] |
Schwartz DC, Cantor CR. Separation of yeast chromosome-sized DNAs by pulsed field gradient gel electrophoresis[J]. Cell, 1984, 37(1): 67-75. DOI:10.1016/0092-8674(84)90301-5 |
| [9] |
Rogakou E P, Boon C, Redon C, et al. Megabase chromatin domains involved in DNA double-strand breaks in vivo[J]. J Cell Biol, 1999, 146(5): 905-915. DOI:10.1083/jcb.146.5.905 |
| [10] |
Crosetto N, Mitra A, Silva MJ, et al. Nucleotide-resolution DNA double-strand break mapping by next-generation sequencing[J]. Nat Methods, 2013, 10(4): 361-365. DOI:10.1038/nmeth.2408 |
| [11] |
Bernal MA, Bordage MC, Brown JMC, et al. Track structure modeling in liquid water: A review of the Geant4-DNA very low energy extension of the Geant4 Monte Carlo simulation toolkit[J]. Phys Med, 2015, 31(8): 861-874. DOI:10.1016/j.ejmp.2015.10.087 |
| [12] |
Incerti S, Ivanchenko A, Karamitros M, et al. Comparison of GEANT4 very low energy cross section models with experimental data in water[J]. Med Phys, 2010, 37(9): 4692-4708. DOI:10.1118/1.3476457 |
| [13] |
Incerti S, Baldacchino G, Bernal M, et al. The Geant4-DNA project[J]. Inter J Model Simul Sci Comput, 2010, 1: 157-178. DOI:10.1142/S1793962310000122 |
| [14] |
Sakata D, Lampe N, Karamitros M, et al. Evaluation of early radiation DNA damage in a fractal cell nucleus model using Geant4-DNA[J]. Phys Med, 2019, 62: 152-157. DOI:10.1016/j.ejmp.2019.04.010 |
| [15] |
Hillier L, Coulson A, Murray J, et al. Genomics in C. elegans: So many genes, such a little worm[J]. Genome Res, 2005, 15(12): 1651-1660. DOI:10.1101/gr.3729105 |
| [16] |
Incerti S, Kyriakou I, Bernal MA, et al. Geant4-DNA example applications for track structure simulations in liquid water: A report from the Geant4-DNA Project[J]. Med Phys, 2018, 45(8): E722-E739. DOI:10.1002/mp.13048 |
| [17] |
Kyriakou I, Sakata D, Tran HN, et al. Review of the Geant4-DNA simulation toolkit for radiobiological applications at the cellular and DNA level[J]. Cancers, 2022, 14(1): 35. DOI:10.3390/cancers14010035 |
| [18] |
Chen JL, Yun SJ, Dong TK, et al. Investigate the radiation-induced damage on an atomistic DNA model by using Geant4-DNA toolkit[J]. Nucl Inst Methods Phys Res B, 2021, 494-495: 59-67. DOI:10.1016/J.NIMB.2021.03.010 |
| [19] |
Sakata D, Belov O, Bordage MC, et al. Fully integrated Monte Carlo simulation for evaluating radiation induced DNA damage and subsequent repair using Geant4-DNA[J]. Sci Rep, 2020, 10(1): 20788. DOI:10.1038/s41598-020-75982-x |
| [20] |
Shin WG, Ramos-Mendez J, Tran NH, et al. Geant4-DNA simulation of the pre-chemical stage of water radiolysis and its impact on initial radiochemical yields[J]. Phys Med, 2021, 88: 86-90. DOI:10.1016/j.ejmp.2021.05.029 |
| [21] |
Ramos-Mendez J, Shin WG, Karamitros M, et al. Independent reaction times method in Geant4-DNA: Implementation and performance[J]. Med Phys, 2020, 47(11): 5919-5930. DOI:10.1002/mp.14490 |
| [22] |
Nikjoo H, Oneill P, Goodhead DT, et al. Computational modelling of low-energy electron-induced DNA damage by early physical and chemical events[J]. Int J Radiat Biol, 1997, 71(5): 467-483. DOI:10.1080/095530097143798 |
| [23] |
Zabihi A, Incerti S, Francis Z, et al. Computational approach to determine the relative biological effectiveness of fast neutrons using the Geant4-DNA toolkit and a DNA atomic model from the Protein Data Bank[J]. Phys Rev E, 2019, 99(5): 052404. DOI:10.1103/PhysRevE.99.052404 |
| [24] |
Pater P, Backstom G, Villegas F, et al. Proton and light ion RBE for the induction of direct DNA double strand breaks[J]. Med Phys, 2016, 43(5): 2131-2140. DOI:10.1118/1.4944870 |
| [25] |
Min H, Sung M, Son M, et al. Transgenerational effects of proton beam irradiation on Caenorhabditis elegans germline apoptosis[J]. Biochem Biophys Res Commun, 2017, 490(3): 608-615. DOI:10.1016/j.bbrc.2017.06.085 |
| [26] |
Zhu K, Wu C, Peng XY, et al. Nanoscale calculation of proton-induced DNA damage using a chromatin geometry model with Geant4-DNA[J]. Int J Mol Sci, 2022, 23(11): 6343. DOI:10.3390/ijms23116343 |
| [27] |
Lampe N, Karamitros M, Breton V, et al. Mechanistic DNA damage simulations in Geant4-DNA part 1: A parameter study in a simplified geometry[J]. Phys Med, 2018, 48: 135-145. DOI:10.1016/j.ejmp.2018.02.011 |
| [28] |
Zhu HY, Mcnamara AL, Ramos-Mendez J, et al. A parameter sensitivity study for simulating DNA damage after proton irradiation using TOPAS-nBio[J]. Phys Med Biol, 2020, 65(8): 085015. DOI:10.1088/1361-6560/ab7a6b |
| [29] |
Meylan S, Incerti S, Karamitros M, et al. Simulation of early DNA damage after the irradiation of a fibroblast cell nucleus using Geant4-DNA[J]. Sci Rep, 2017, 7(1): 11923. DOI:10.1038/s41598-017-11851-4 |
| [30] |
王蕴楠. 质子辐射致DNA链断裂损伤的模拟研究[D]. 哈尔滨: 哈尔滨工程大学, 2017. Wang YN. Simulation study on DNA strand breakage induced by proton radiation[D]. Harbin: Harbin Engineering University, 2017. |
| [31] |
唐菁. 质子诱导DNA集簇性损伤的蒙特卡罗模拟研究[D]. 太原: 中北大学, 2020. Tang J. Monte Carlo simulation study of proton-induced clustered DNA damage[D]. Taiyuan: North University of China, 2020. |
| [32] |
唐菁, 马骥祥, 李志媛, 等. 基于DNA双链断裂损伤簇的相对生物效能模拟计算[J]. 中华放射医学与防护杂志, 2023, 43(7): 489-498. Tang J, Ma JX, Li ZY, et al. Simulation calculation of relative biological effectiveness based on DNA double strand breakclusters[J]. Chin J Radiol Med Prot, 2023, 43(7): 489-498. DOI:10.3760/cma.j.cn112271-20230220-00039 |
| [33] |
Shamshiri P, Forozani G, Zabihi A. An investigation of the physics mechanism based on DNA damage produced by protons and alpha particles in a realiatic DNA model[J]. Nucl Instrum Meth Phys Res B, 2019, 454: 40-44. DOI:10.1016/j.nimb.2019.04.086 |
| [34] |
Jones DTL. Fast neutron and proton therapy sources[J]. Radiochim Acta, 2001, 89(4-5): 265-277. DOI:10.1524/ract.2001.89.4-5.265 |
| [35] |
Mohan R, Grosshans D. Proton therapy—present and future[J]. Adv Drug Deliv Rev, 2017, 15(109): 26-44. DOI:10.1016/j.addr.2016.11.006 |
| [36] |
International Commission on Radiological Protection. ICRP Publication 92. Relative biological effectiveness (RBE), quality factor (Q), and radiation weighting factor (wR)[J]. Ann ICRP, 2003, 33(4): 1-117. DOI:10.1016/s0146-6453(03)00024-1 |
| [37] |
Valentin J. The 2007 Recommendations of the International Commission on Radiological Protection. ICRP publication 103[J]. Ann ICRP, 2007, 37(2-4): 1-332. DOI:10.1016/j.icrp.2007.10.003 |
 2024, Vol. 44
2024, Vol. 44


