重离子与物质相互作用时将能量传递给靶物质使其电离，且能量损失主要集中在射程末端，因此在深度剂量分布上射程末端形成Bragg峰，远端边缘急剧下降^[1-2]。重离子的传能线密度高，相对生物效应明显^[3-4]。随着各种放射治疗技术的发展，越来越多的证据显示重离子治疗在肿瘤治疗中取得了显著疗效^[5-6]。

⁹C重离子是一种特殊的重离子治疗束，该重离子束不仅具有一般重离子的特性——形成Bragg峰，还能在射程末端衰变发射两个能量为1.60 MeV的α粒子和一个能量为8.20 MeV(60%)或1.10 MeV(40%)的质子，半衰期(T_1/2)为126.5 ms，离子束穿过人体到达肿瘤区域时间为10^-5ms数量级，因此衰变过程几乎在肿瘤区域完成^[7]。低能α粒子和质子具有很高的相对生物效应(一般为4~6)，在小范围内沉积的能量可导致细胞内辐射敏感靶的团簇损伤，而细胞自身的修复机制无法修复这些团簇损伤^[8]。本研究首先采用蒙特卡罗程序分别模拟多种能量α粒子在细胞中的输运后细胞核内吸收剂量，将结果与美国核医学会医学内照射剂量学(medical internal radiation dose, MIRD)委员会方法的单位累积活度的细胞剂量(S值)进行比较，证明蒙特卡罗模拟的可行性，然后分析⁹C在V79细胞模型的细胞表面、细胞质以及细胞核3种不同位置衰变发出的缓发粒子的能量沉积和细胞的损伤效应，为⁹C离子治疗中缓发粒子相关情况提供微剂量研究的理论依据。

MIRD方法是一种计算S值的连续慢化，近似半解析算法(CSDA)^[9]。MIRD方法计算公式中，平均辐射吸收剂量D计算公式为：

式中，S为S值，Gy/Bq；$ \tilde{A} $为累计活度，Bq。S值取决于辐射的类型和输运特性。它可以定义为每个衰变粒子对靶区的剂量贡献：

式中，Δi为第i个辐射分量的平均能量，Gy；Øi(r_T←r_s)为源区域(r_S)发出的能量被目标区域(r_r)吸收的比例；m_r为目标区域的质量，g。

根据MIRD委员会的建议并结合本研究α在细胞核中的吸收剂量，源区(α粒子随机产生区域)为细胞表面(CS)、细胞质(Cy)和细胞核(N)，细胞核为靶区域(α粒子输运过程造成细胞核中的能量沉积情况)。计算3种源-靶组合的细胞S值：细胞质到细胞核(N←Cy)，细胞表面到细胞核(N←CS)，细胞核到细胞核(N←N)。MIRD方法计算模型为双球均质模型，是由细胞核(半径为R_N)和细胞(半径为R_C)组成的两个同心球体^[9-10]。

采用基于蒙特卡罗方法的particle and heavy ion transport code system(PHITS软件)，由日本原子能机构(JAEA)、日本信息科学与技术研究组织(RIST)、日本高能加速器研究机构(KEK)等研究机构合作开发的通用蒙卡粒子输运模拟代码。该软件在核领域具有强大的模拟计算功能，可以模拟宽能量范围内各种粒子包括光子、电子、中子、质子和重离子的输运。应用于核医学物理的各个领域包括不同类型放射治疗、屏蔽计算、辐射生物学以及医疗器械研发，模拟中子、光子以及一些带电粒子在靶物质中输运过程最后计算靶物质吸收剂量情况等^[11-12]。本研究根据 ⁹C离子治疗中缓发粒子类型和能量等信息设置程序指令，粒子发射方向为各向同性，分别在细胞核内、细胞质内以及细胞表面随机抽样发射粒子。

将细胞模型理想化近似为一个双同心球型结构，细胞膜厚度约为0.01 μm，细胞直径约为13 μm，细胞核直径约为9 μm，则细胞质厚度(即细胞膜到细胞核距离)约为2 μm ^[13-14]。细胞各部位物质组成成分：细胞膜主要成分是膜磷脂，化学式为C₄₁H₈₀O₈P；细胞质主要包含基质和细胞器，主要成分是水，其他元素含量极少，此处直接用水代替细胞质简化模拟；细胞核主要由染色体，核仁以及核骨架组成，主要化学成分有碳、氢、氧、氮、磷、硫等^[15-17]。

模拟抽样入射α粒子或质子在细胞内输运。本研究中，由于细胞膜厚度较小，入射粒子穿过细胞膜与细胞膜内原子发生弹性散射，只减少一小部分能量，粒子继续进入细胞质和细胞核并与靶原子发生非弹性散射和弹性散射，导致绝大部分能量损失在细胞内。细胞内的能量沉积分布包括粒子与核外电子非弹性散射、级联运动原子与核外电子非弹性散射的能量损失^[18]。首先使用PHITS分别模拟计算能量范围为3~10 MeV的α粒子在细胞各个区域(细胞表面、细胞质和细胞核)中输运后在细胞核内平均吸收剂量结果，对比MIRD方法证明该模型可行性。然后，分别模拟⁹C在细胞外、细胞质内以及细胞核内等3种不同位置一次衰变发出的缓发粒子(α粒子和质子)的能量沉积情况。

DNA双链断裂(DNA double-strand breaks, DSBs)属于电离辐射在细胞核DNA中引起的初始损伤。Wang等^[19]结合辐射诱导DNA双链断裂和分子理论线性二次方程(LQ)模型，通过来自于粒子辐照数据集合(particle irradiation data ensemble, PIDE，该数据库包含了世界各地不同实验室使用不同细胞类型和不同离子在不同能量下进行的800多个细胞生存实验的结果)确定模型的拟合参数，提出新的辐射诱导DSBs后细胞存活的机制。具体公式如下：

式中，α为早反应损伤系数；β为晚反应损伤系数；D为单次吸收剂量，Gy；FS为细胞存活系数。早反应损伤系数α计算如下：

晚反应损伤系数β计算如下：

式中，μ_x为同一DSBs的另一端正确连接的平均概率；μ_y为错误修复灵敏度；ζλ_p为非辐射导致DSBs的概率；ξλ_p为DSBs末端与由相同初级粒子诱导的不同DSBs末端连接的平均概率；η(λ_p)为DSBs末端与不同初级粒子诱导的DSBs末端连接的平均概率；λ_p为每个初级粒子产生的DSBs的平均数；λ为每个细胞每个初级粒子径迹DSBs产额；Y为每细胞每Gy的DSBs产额。

Wang等^[19]通过粒子辐照数据集合(PIDE)实验数据确定模型的拟合参数，即V79细胞在辐射诱导的DSBs之后的细胞存活模型的参数分别为：μ_x=0.956 8±0.023 6，μ_y=0.030 0±0.017 7，ζ=0.041 2±0.020 9，ξ=0.060 8±0.038 1，η_λp→1=(9.78±0.10)×10^-4，η_λp→∞=0.006 5±0.000 1。DNA双链断裂(DSBs)产额Y和每个细胞每个初级颗粒的DSBs产率λ可以由美国华盛顿大学开发的快速蒙特卡罗损伤模拟软件(the fast Monte Carlo damage simulation software, MCDS)计算得出^[20]。本研究根据此机制结合α粒子和质子在细胞核内平均吸收剂量计算分析V79细胞模型的细胞存活率情况。

表 1是3~10 MeV的α粒子在细胞各个区域(细胞表面、细胞质和细胞核)中输运后在细胞核内平均吸收剂量与MIRD出版物^[9]S值的比较，其中细胞半径R_C=10 μm, 细胞核半径R_N=5 μm。结果显示，PHITS和MIRD方法计算细胞中α粒子的细胞S值百分比差异为-1.99%~5.11%，表明PHITS可用于准确模拟计算细胞能量沉积。并且MIRD方法是一种连续减速近似(CSDA)数值计算方法，忽略了二次电子、X射线和能量损失离散的影响^{[9, 21]}。蒙特卡罗模型充分考虑了二次电子和X射线的影响，蒙特卡罗方法充分考虑粒子输运，抽样方法以及调用权威的JENDL核数据库中的反应截面，更加真实地模拟粒子在输运时与靶物质各元素相互作用结果，导致PHITS计算的S值略高于MIRD。从表 1可以看出，部分PHITS得到的结果小于MIRD的S值(百分比差异为负数)，尤其是S_N←CS，原因是PHITS在细胞表面模拟抽样粒子时，考虑到α粒子出射为各向同性导致有部分粒子逃逸出了细胞。

表 1(Table 1)

表 1 PHITS和MIRD方法计算细胞中不同能量α粒子的细胞S值及其偏差(%，RC=10 μm, RN=5 μm) Table 1 Cellular S values of α particles with different energies in the cell calculated using PHITS and MIRD methods and their percentage differences (%, RC = 10 μm, RN = 5 μm) α粒子能量(MeV) SN←N SN←Cy SN←CS MIRD (Gy/Bq) PHITS (Gy/Bq) 偏差(%) MIRD (Gy/Bq) PHITS (Gy/Bq) 偏差(%) MIRD (Gy/Bq) PHITS (Gy/Bq) 偏差(%) 3 1.57×10-1 (1.60±0.003) ×10-1 1.91 4.06×10-2 (4.12±0.007) ×10-2 1.48 2.51×10-2 (2.46±0.038) ×10-2 -1.99 4 1.25×10-1 (1.28±0.002) ×10-1 2.40 2.99×10-2 (3.06±0.005) ×10-2 2.34 1.74×10-2 (1.71±0.005) ×10-2 -1.72 5 1.05×10-1 (1.08±0.002) ×10-1 2.86 2.44×10-2 (2.52±0.005) ×10-2 3.28 1.37×10-2 (1.36±0.006) ×10-2 -0.73 6 9.11×10-2 (9.46±0.023) ×10-2 3.84 2.08×10-2 (2.16±0.016) ×10-2 3.85 1.16×10-2 (1.15±0.005) ×10-2 -0.86 7 8.10×10-2 (8.45±0.020) ×10-2 4.32 1.83×10-2 (1.91±0.014) ×10-2 4.37 1.01×10-2 (1.00±0.006) ×10-2 -0.99 8 7.34×10-2 (7.63±0.018) ×10-2 4.06 1.64×10-2 (1.72±0.008) ×10-2 4.88 9.00×10-3 (9.05±0.052) ×10-3 0.56 9 6.68×10-2 (6.99±0.016) ×10-2 4.75 1.49×10-2 (1.56±0.006) ×10-2 4.70 8.15×10-3 (8.21±0.022) ×10-3 0.74 10 6.16×10-2 (6.46±0.015) ×10-2 4.95 1.37×10-2 (1.44±0.002) ×10-2 5.11 7.48×10-3 (7.54±0.020) ×10-3 0.80 注：MIRD.美国核医学会医学内照射剂量学；PHITS项的模拟值格式为x±s，表示最佳模拟数值±标准差拟合不确定度；N.细胞核；Cy.细胞质；CS.细胞表面

表 1 PHITS和MIRD方法计算细胞中不同能量α粒子的细胞S值及其偏差(%，RC=10 μm, RN=5 μm) Table 1 Cellular S values of α particles with different energies in the cell calculated using PHITS and MIRD methods and their percentage differences (%, RC = 10 μm, RN = 5 μm)

使用PHITS程序并根据V79细胞参数建立细胞模型，模拟计算出⁹C离子在不同位置衰变导致细胞核内平均吸收剂量的情况见表 2。⁹C随机在细胞表面、细胞质或细胞核内一次β⁺衰变各向同性发出3个缓发粒子(两个α粒子和1个质子)，并在V79细胞模型中输运，结果显示⁹C离子在细胞核内衰变导致细胞核内平均吸收剂量远大于其他两个衰变位置。对于不同能量的质子，1.10 MeV的质子在细胞中输运造成的细胞内吸收剂量大于能量为8.20 MeV的质子，其原因是能量越高质子的射程越长，导致能量几乎损失在较远端的其他细胞中。

表 2(Table 2)

表 2 9C离子于细胞不同位置各个缓发粒子产生的核内平均吸收剂量(Gy，x±s) Table 2 Mean endonuclear absorbed doses of delayed particles from the decay of 9C-ions at different sites of the cell (Gy, x±s) 缓发粒子 细胞核内(N←N) 细胞质内(N←Cy) 细胞表面(N←CS) 2个α粒子(1.60 MeV) (4.19±0.011)×10-1 (1.42±0.001)×10-1 (8.35±0.017)×10-2 1.10 MeV质子 (2.64±0.007)×10-2 (9.89±0.017)×10-3 (6.73±0.032)×10-3 8.20 MeV质子 (5.69±0.014)×10-3 (2.06±0.003)×10-3 (1.37±0.007)×10-3 注：N. 细胞核；Cy. 细胞质；CS. 细胞表面

表 2 9C离子于细胞不同位置各个缓发粒子产生的核内平均吸收剂量(Gy，x±s) Table 2 Mean endonuclear absorbed doses of delayed particles from the decay of 9C-ions at different sites of the cell (Gy, x±s)

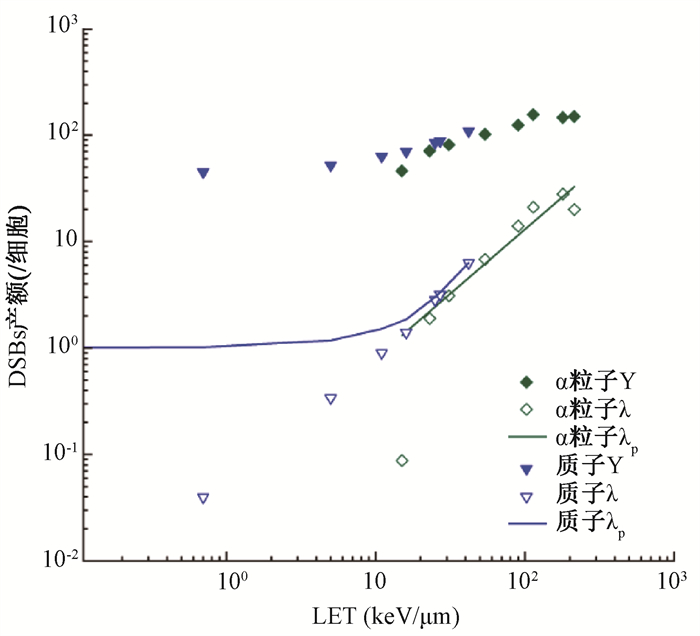
根据V79细胞模型设置快速蒙特卡罗损伤模拟(MCDS)软件，计算不同射线LET与每个细胞双链断裂(DSBs)各种类型产额关系(图 1)。实心倒三角形与菱形分别表示用质子与α粒子辐照的V79细胞的每Gy的DSBs产额Y，具有相同颜色的空心表示每个轨道的DSBs产额λ，具有相同颜色的实线表示由引起DSBs的每个初级粒子产生的DSBs的数量λ_p。对于LET < 10 keV/μm的质子，每个径迹的DSBs产额随着LET迅速增加，但是由于低LET质子生物学效应与光子相似或略高于光子的原因，λ_p数据增加非常缓慢且略高于1，这与光子趋势相似。对于高LET辐射质子与α粒子，λ和λ_p之间的差异较小。最后将表 2中各沉积能量结合辐射诱导DNA双链断裂(DSBs)后细胞存活的机制模型公式(1)~(7)，分析出V79细胞模型生存情况(其中采用加权方法处理不同粒子在细胞核内吸收剂量的影响)。当一个⁹C离子在细胞表面衰变产生次级粒子进入细胞，产生的质子初始能量为1.10和8.20 MeV情况下，计算细胞生存率约为88%。由于质子射程远大于细胞尺寸，主要能量损失可能出现在远端细胞中，因此两种不同能量质子对细胞生存率影响较小。若衰变在细胞质中进行，产生的这两种初始能量质子计算得出细胞生存率为80.62%~80.90%。当⁹C离子直接进入细胞核中心处衰变，α粒子射程短并将大部分能量沉积在细胞中，造成细胞损伤最大，细胞存活的概率约为53%。

图 1 辐射诱导的V79细胞模型DSBs产额 Figure 1 Yields of radiation-induced DSBs in the V79 cell model

重离子治疗无论是在集中杀死肿瘤细胞方面，还是有效保护肿瘤周围正常组织方面都有很明显的效果，是当今正在大力发展的放疗手段。α粒子具有射程短，内照射损伤大等特点，进入细胞内与细胞中各原子相互作用能量耗尽最终停留在细胞里。随着粒子与靶物质相互作用，将能量传递给靶原子，自身能量逐渐减小，电离效应增强直到射程末端形成最大值区。峰值尾端能量进一步减小且不足以使靶原子电离，最终停留在细胞中被组织吸收。

⁹C重离子是以能量为430 MeV/u的¹²C离子作为初级束，并与铍靶反应产生⁹C。目前，射束强度尚未达到肿瘤治疗要求，仍处于研究阶段，若突破相关技术困难，该方法在治疗肿瘤方面具有巨大的潜力。⁹C是双重辐射源重离子束，自身衰变产生的缓发粒子能对肿瘤细胞进行内照射，进而提供更高的相对生物效应，其相对生物学效能(RBE)较¹²C重离子束流高2倍以上^[7]。本研究主要针对⁹C重离子衰变产物在亚细胞水平上进行模拟研究，由于在亚细胞水平上实验观测细胞的损伤情况较为困难，因此采用可信度较高的蒙特卡罗方法建立细胞模型，模拟缓发粒子在细胞中输运的可能性，最终借助模拟结果分析细胞可能的损伤及死亡情况。结果显示，⁹C重离子在细胞核中心处衰变，α粒子射程短并将大部分能量沉积在细胞中，细胞存活的概率约为50%。由于质子射程较长，能量几乎均损失在较远端的细胞，质子仅穿过细胞核对细胞影响小，射程末端则可造成较大损伤。Li等^[7]和李强等^[8]在研究关于⁹C离子束辐照生物学效应及相关生物物理机制中发现，当照射剂量为2 Gy的⁹C离子束照射人类唾液腺细胞时，每个细胞中平均沉积的⁹C离子数为0.748个，在这种情况下缓发粒子致死率进一步降低，若提高照射剂量或束流强度会增加其致死效率。Munro^[22]在细胞质和细胞核射线相对敏感度的一系列精细实验研究中发现，细胞核对射线的敏感性是细胞质的300多倍。可以近似认为核外能量沉积对哺乳动物细胞的修复能力无影响，因此本研究忽略细胞质沉积能量重点考虑α粒子和质子在细胞核内的影响。

本研究以简化模型模拟计算的形式从物理角度直观量化⁹C离子缓发粒子对细胞的影响。仍存在一定局限性，缓发粒子在细胞中输运是一个复杂多变的过程，且未从生物学角度考虑能量沉积等相关影响，还需要进一步结合理论知识和实验数据深入探究内照射对细胞的作用机制。

利益冲突  无

作者贡献声明  张毅负责设计研究方案、研究实施及论文撰写；游士虎、罗元强、王志勇负责模拟运算与程序调试；许聪凤、金海洁、张皓嘉负责数据采集与整理；洪卫、甘家应、胡银祥指导论文写作，参与论文修改