在碳达峰和碳中和的“双碳”目标大背景下,核能作为一种安全、清洁、经济的能源,越来越得到全世界的广泛认可和接受[1-2]。然而,核设施的运行通常会产生一定量的含氚废水。针对周围没有江河湖泊等受纳水体的空旷内陆厂址,逐步发展出采用大气载带排放的方式来替代常规的液态途径排放[3-4]。为实现这一液转气的排放过程,目前提出了一种采用高压微雾载带的方式将高压水流破碎成微米级微雾[5-6],与此同时,加热后的载带气与微雾接触,使含氚微雾汽化,载带气含湿量增加,最终用排风机将增湿后的气体送往烟囱进行高架排放。由于此类排放的高度较高,对周边环境的影响较小,然而,这一方法若处理不好,可能会使微雾尚未蒸发就进入大气环境,从而因微雾相比于气体更易于在近区沉降而显著增加近区污染[7]。根据前期研究,超过100 μm的微雾在重力作用下会很快沉降[8-9]。为此,需要跟踪和研究微雾在排入大气之前的蒸发特性,以了解和确认微雾在排入大气之前能否完全蒸发。
本研究为探究含氚废水微雾在水平蒸发室及竖直烟囱内的蒸发情况,针对含氚废水微雾的蒸发特性,模拟水平蒸发室条件,进行实验台架搭建,并且结合实验数据,采用Fluent(美国Ansys公司)中的离散相模型(discrete phase model,DPM),构建合适的蒸发模型,随后应用该蒸发模型对工程设计蒸发室进行蒸发情况模拟,由此给出在给定工况下的蒸发实效,为今后内陆核设施净化后含氚废水载带排放的工程应用提供重要参考。
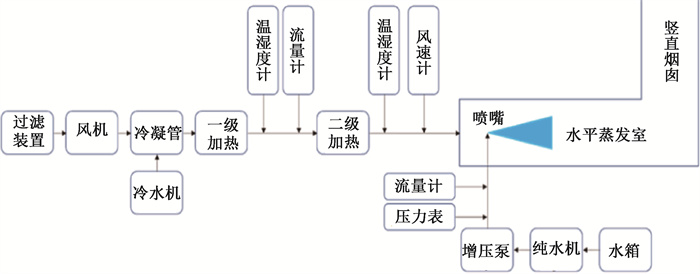
材料与方法1. 蒸发实验系统及设备:本次实验搭建了一个水平段最长可达10 m,竖直段最长可达5 m的透明管段实验台,用以模拟和确认单个喷嘴喷射微雾的蒸发特性和粒径变化,如图 1所示。其中,水平管段和竖直管段是由0.6 m×0.6 m的透明亚克力方管依次连接而成,单一的喷嘴安装在管道中心。实验中,以轻水模拟净化后的含氚废水,通过增压泵和实际采用的喷嘴产生需要的粒径与流量,进而与冷凝除湿并加热后的载带气接触,使微雾不断蒸发,粒径减小,同时载带气含湿量增加,用排风机将增湿后的气体送往烟囱进行高架排放。本次蒸发实验及数值模拟主要针对高架烟囱排放之前的水平蒸发室及竖直烟囱内微雾特性进行研究。
|
图 1 单喷嘴缩比实验系统及流程示意图 Figure 1 Single nozzle scaling experimental system and flowchart |
微雾在输运蒸发过程中最关键的参数是粒径的变化,可表征微雾表面与载带空气来流之间传递质量的多少,即微雾的蒸发量。激光散射粒度仪(珠海欧美克仪器有限公司,OMEC-DP02)的基本原理是不同粒径微雾对准直激光的散射程度不同,但当微雾较为稀疏时,测量结果可能缺乏代表性,故激光散射粒度仪的测量主要是针对喷雾出口不远处(1~3 m)微雾密集区域进行测量;对于水平蒸发室末端是否还存在微雾雾滴的确认,采用直接光学拍摄。利用连续激光器产生绿色片光源,通过高像素相机(日本SONY公司,A7R4)和长焦镜头连续获得400张光学照片,经MATLAB(美国MathWorks公司)进行灰度变换、灰度梯度滤波、二值化后,计量其中单连通区域的光照强度,根据微雾散射光强度与微雾粒径平方及微雾浓度成正比的原理,即可构建雾滴粒径和光照强度的关系[10]。
对于单喷嘴缩比实验,由于实验管段空间有限,水平喷嘴位于三维方管的中心,距离方管底面只有0.3 m,部分微雾由于偏下的初始喷射角度以及聚并导致的粒径增大等原因存在沉降到底部的情况,为此,有必要通过测量方管底面的吸水剂前后的质量差计算沉降的雾滴质量。
2. 实验系统相似性分析:微雾蒸发是一种通过微雾表面与环境进行能量交换和质量交换的行为,通常被描述为微雾表面水浓度向环境的扩散过程,这一过程会导致微雾粒径变小,相应地,其逆过程被称为冷凝。微雾蒸发的关键在于求解下述两个方程[11]:
传热方程:
| $ m_{\mathrm{p}} c_{\mathrm{p}} \frac{\mathrm{d} T_{\mathrm{p}}}{\mathrm{d} t}=h A_{\mathrm{p}}\left(T_{\mathrm{a}}-T_{\mathrm{p}}\right)-\\ \frac{\mathrm{d} m_{\mathrm{p}}}{\mathrm{d} t} h_{\mathrm{fg}}+\varepsilon_{\mathrm{p}} A_{\mathrm{p}} \sigma\left(\theta_{\mathrm{R}}^4-T_{\mathrm{p}}^4\right) $ | (1) |
传质方程:
| $ \begin{gathered} N_{\mathrm{i}}=k_{\mathrm{c}}\left(C_{\mathrm{i}, \;\mathrm{s}}-C_{\mathrm{i}, \;\mathrm{a}}\right), C_{\mathrm{i}, \;\mathrm{s}}= \\ \frac{p_{s a t}\left(T_{\mathrm{p}}\right)}{R T_{\mathrm{p}}}, C_{\mathrm{i}, \;\mathrm{a}}=X_{\mathrm{i}} \frac{p}{R T_{\mathrm{a}}} \end{gathered} $ | (2) |
式中,mp为微雾粒子质量,kg;cp为微雾粒子的比热容,J·kg-1·K-1;h为对流换热系数,W·m-2· K-1;Ap为微雾表面积,m2;Ta为载带气温度,K;hfg为汽化潜热,J/kg;εp为辐射的角系数,σ为史提芬-玻尔兹曼常数(5.67×10-8 W·m-2·K-4),θR为辐射温度,K;Ni为微雾的摩尔通量,mol·m-2·s-1;kc为传质系数,m/s;Ci, s为微雾表面的水蒸汽浓度,mol/m3;Ci, a为载带气中的水蒸汽浓度,mol/m3;R为理想气体常数,J· mol-1·K-1;Xi为该组分i的局部体积摩尔分数;p为当地压强,Pa。在本实验中,辐射换热带来的影响微乎其微,可忽略。
在上述方程中,微雾的表面积和质量可由微雾粒径直接得到,气体常数为恒值,当地压力几乎不变,待求未知量为微雾的粒径和温度,局部组分体积分数可由微雾粒径的变化求得。因此,微雾蒸发的传热和传质过程问题本质上就是对流换热系数h和传质系数kc在不同工况下的取值,这两个取值可由舍伍德数Sh0和努赛尔数Nu两个无量纲数表示[12]:
| $ S h_0=\frac{2 h_{\mathrm{m}} R_{\mathrm{d}}}{D_{\mathrm{Fa}}}, N u=\frac{h R_{\mathrm{d}}}{k} $ | (3) |
在目前的各种模型中,包括仅依靠实验数据的半经验模型,舍伍德数Sh0通常与微雾雾滴的雷诺数Red=2Rd|vd-vg|/νg和施密特数Scd=vg/DFa等无量纲数有关,努赛尔数Nu通常与微雾雾滴的雷诺数Red和普朗特数Prd=cpgμg/kg有关。在后续研究中,分别针对其关系式,添加了斯伯丁传热系数BT和斯伯丁传质系数Bm的修正[13]:
| $ B_{\mathrm{T}}=\frac{c_{\mathrm{p}}\left(T_{\mathrm{g}}-T_{\mathrm{s}}\right)}{L_{\text {eff }}}, \quad B_{\mathrm{m}}=\frac{Y_{\mathrm{i}, \;\mathrm{s}}-Y_{\mathrm{i}, \;\mathrm{a}}}{1-Y_{\mathrm{i}, \;\mathrm{s}}} $ | (4) |
式中,Yi, s为微雾表面的水蒸气份额;Yi, a为载带气的水蒸气份额;Leff为有效汽化潜热,J/kg,Leff=hfg-
以某一微雾蒸发模型为例[14]:
| $ \begin{gathered} S h_0=2\left(1+0.3 R e_{\mathrm{d}}^{\frac{1}{2}} S c_{\mathrm{d}}^{\frac{1}{3}}\right) \\ N u=2 \frac{\ln \left(1+B_{\mathrm{M}}\right)}{B_{\mathrm{M}}}\left(1+0.3 Re_{\mathrm{d}}^{\frac{1}{2}} Pr_{\mathrm{d}}^{\frac{1}{3}}\right) \end{gathered} $ | (5) |
对于以上各系数,在微雾的材质与载带气流的材质确定的情况下,施密特数Scd与普朗特数Prd为确定值。为确保舍伍德数Sh0和努赛尔数Nu相等,只需要保证微雾雷诺数Red相等即可。由于微雾材质确定,而微雾的粒径以及喷嘴的出口速度难以控制,故采用相同型号的喷嘴,保证同样风速以保证雷诺数相等。
确保了相同舍伍德数Sh0和努赛尔数Nu,即确保了微雾的蒸发速率,为确保微雾蒸发和实际蒸发的相似性,还需要保证微雾在管段内的蒸发时间相同。由于在微雾雷诺数Red中确定了载带气流度,保证管段长度即可保证微雾蒸发时间相同。
在不考虑微雾蒸发的情况下,对于微雾在风道内的流动,运动方程可以表示为[15]:
| $ m_p \frac{\mathrm{d} \vec{u}_{\mathrm{p}}}{\mathrm{d} t}=m_p \frac{f\left(\vec{u}-\vec{u}_{\mathrm{p}}\right)}{\tau_{\mathrm{s}}}+m_p \frac{\vec{g}\left(\rho_{\mathrm{p}}-\rho\right)}{\rho_{\mathrm{p}}} $ | (6) |
式中,
经无量纲化后,方程变化为:
| $ \frac{\mathrm{d} \vec{u}_{\mathrm{p}} \times(t)}{\mathrm{d} t}=\frac{f T_{m E}}{\vec{u}_p \tau_{\mathrm{s}}}\left(\vec{u}-\vec{u}_p\right)+\frac{\vec{g} T_{m E}}{\vec{u}_{\mathrm{p}}} \frac{\left(\rho_{\mathrm{p}}-\rho\right)}{\rho_{\mathrm{p}}} $ | (7) |
式中,TmE为欧拉积分时间尺度,随着微雾雷诺数Red变化,在1<Red<800时,f =1+0.15×Red0.687。这个无量纲式中引入了一个无量纲数斯托克斯数
直观而言,斯托克斯数表示了微雾粒子在流场中的载带性,斯托克斯数越大,微雾粒子自身惯性效果越强;相应地,斯托克斯数越小,微雾粒子载带性就会越好。在实验台管段中,斯托克数约为10-4量级,在工程设计中,斯托克斯数约为10-8量级,二者虽然相差了4个量级,但事实上当斯托克斯数足够小的时候,即可认为微雾完全跟随载带气体流动,根据现有研究,当斯托克斯数<0.1时,载带误差即<1%[16]。
同时在微雾的流动中,还需要考虑弗劳德数
对于风道载带气体的雷诺数,为使实验管段(1.5 × 106)与工程设计(2.0 × 107)雷诺数相同,需要将实验管段风速与管段长度变为工程设计值的13.3倍,同时速度的变化会导致弗劳德数Fr发生变化,对于弗劳德数Fr,重力加速度无法改变,在改变速度时只能通过改变微雾粒径实现二者相等,二者发生冲突,而微雾的速度和粒径与喷嘴选型相关,不容易控制,即使是同一喷嘴,也会因压力不同而有所变化。加之载带气在风管内的流动情况并不是本实验的研究重点,且在雷诺数>105后,雷诺数达到自准区间[17],高压微雾在实验管段与工程设计中的湍流载带高度相似。
综上所述,本实验段的参数选取完全保证了微雾在蒸发中的相似性,工程设计和实验系统中喷雾产生系统的喷雾粒径、喷出速度、喷出方式和雾滴温度无差异,载带气温度、湿度、风速无差异,保证了微雾在载带气体中湍流扩散的相似性,如表 1所示。
|
|
表 1 基于高压微雾的蒸发实验系统与工程设计的差异性比较 Table 1 Comparison of differences between experimental evaporation system and engineering system |
3. 微雾载带蒸发计算模型和工具:本次数值模拟采用Ansys Fluent 2022 R1进行水平蒸发室内单喷嘴条件下的微雾载带和蒸发模拟。该工况为两相流,由于载带工况下的微雾所占份额较小,相对稀疏,适合采用DPM[18]进行模拟,即采用欧拉方法对载带流场进行求解,采用拉格朗日方法对微雾位置进行追踪。其中,连续相气体的流动通过求解连续性方程公式(8)和动量守恒方程公式(9)获得,计算域中还涉及连续相和颗粒相间的能量传输,因此,还需求解能量守恒方程,如公式(10)所示。采用ICEM对缩比实验管段进行网格划分,对喷嘴所在位置以局部网格细化的方式进行加密,保证了数值模拟计算的可靠性,经验证网格质量符合要求。求解过程采用Coupled压力基耦合算法,压力项采用二阶格式,动量和能量项采用二阶迎风格式,湍动能项、湍流耗散率和雷诺应力项采用一阶迎风格式。湍流模型采用Realizable k-ε,同时,由于微雾雾滴较小,其扩散情况受湍流影响较大,引入Fluent中DPM下的离散随机轨迹(discrete random walk,DRW)模型。该模型根据脉动速度分量是离散的时间分段常数函数,通过对单个粒子的轨迹方程进行积分,利用积分过程中沿粒子路径的瞬时流体速度来预测粒子的湍流扩散。通过这种方式计算足够数量的代表性粒子的轨迹,可以包括湍流对粒子弥散的随机影响。对于单喷嘴蒸发实验的验证工况,其进口温度为31.44℃,相对湿度为68.14%,载带空气流量为1 430.62 m3/h,边界条件入口设置为速度入口1.10 m/s,喷嘴流量为4.04 kg/h,出口边界条件设置为压力出口,压力值为0,其余为壁面,采用无滑移绝热壁面,设置微雾碰撞后的作用类型为反射。
| $ \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho \vec{v})=S_{\mathrm{m}} $ | (8) |
| $ \frac{\partial}{\partial t}(\rho \vec{v})+\nabla \cdot(\rho \vec{v} \vec{v})=-\nabla p+\nabla \cdot(\overline{\bar{\tau}}) $ | (9) |
| $ \begin{gathered} \frac{\partial}{\partial t}\left[\rho\left(e+\frac{v^2}{2}\right)\right]+\nabla \cdot\left[\rho v\left(h+\frac{v^2}{2}\right)\right]= \\ \nabla \cdot\left(k_{\mathrm{eff}} \nabla T-\sum_{\mathrm{j}} h_{\mathrm{j}} \vec{J}_{\mathrm{j}}\right)+S_{\mathrm{h}} \end{gathered} $ | (10) |
式中,ρ为连续相气体密度,kg/m3;
1. 单喷嘴蒸发特性缩比实验的数值模拟
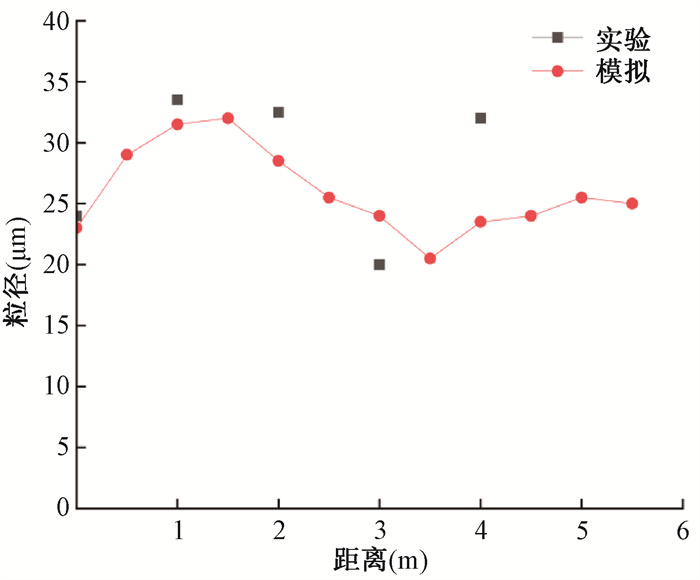
(1) 雾滴粒径变化的模拟验证:以实验工况温度30.1℃,空气含湿量19.97 g/kg,风速2.17 m/s,喷嘴流量2.9 kg/h为例。将距离喷嘴各典型距离点处激光散射粒度仪测量的索特平均直径结果与数值模拟结果进行对比分析,实验系统采用的是激光散射粒度仪的测量结果,计算统计1 s内所有通过长度贯穿整个实验管段、高度为0.5 mm的片状空间的雾滴,对其求索特平均直径,结果如图 2所示。根据现有研究,激光散射粒度仪在遮光比超过6%时测量结果是可靠的,这点在实验中也有所体现。在喷嘴出口到3 m的区间,二者对应较好,但在3 m以后,由于遮光比较低,采样率不足,数据波动较大。导致喷射初期粒径增大的原因,一方面是由于早期存在聚并过程,另一方面是由于小粒径的雾滴迅速蒸发,中等及较大粒径的雾滴蒸发较慢;最后阶段趋于平稳则是由于大粒径雾滴完全沉降,小粒径雾滴完全蒸发,只有少量中等粒径雾滴,既不能快速蒸发,也不能迅速沉降。
|
图 2 粒度仪测量结果与数值计算结果对比图 Figure 2 Comparison between the the particle size analyzer-based measurement results and the numerical simulation results |
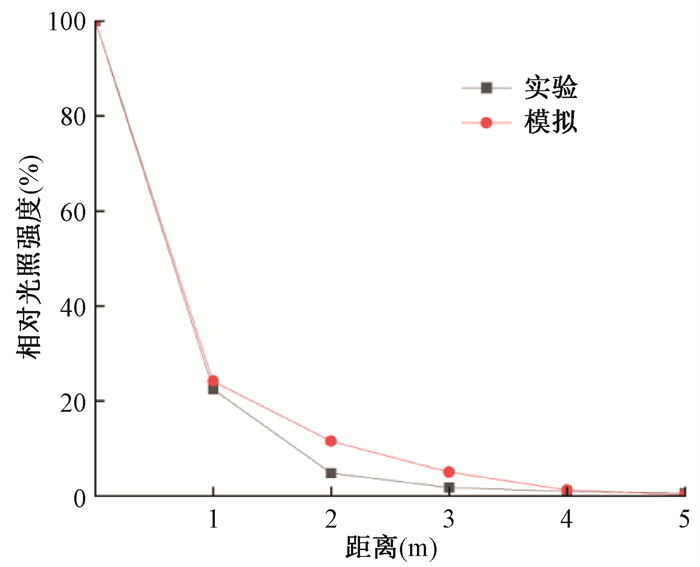
(2) 雾滴散射光强度变化的模拟验证:基于微雾散射光强度(物理实验可实现)与微雾粒径平方及微雾浓度成正比(数值模拟可实现)的原理[10],统计各距离下片激光拍摄400张图片的中心处约3 cm×3 cm方块区域的光照强度,并与初始段的光照强度相除得到一个相对光照强度,与数值模拟结果中对应区域的雾滴数目乘以雾滴粒径的平方和,也与初始段的统计结果相除得到一个相对百分比,二者分别代表物理实验实测的相对光照强度和数值模拟的相对光照强度,对比结果如图 3所示。从中可以看出,数值模拟与实验结果吻合较好,相对光照强度随距离增加大致呈指数减小,说明微雾蒸发速度较快,粒径和浓度均快速减少。
|
图 3 实测相对光照强度和数值模拟结果随距离变化对比图 Figure 3 Comparison between measured relative light intensity and numercial simulation results with distance |
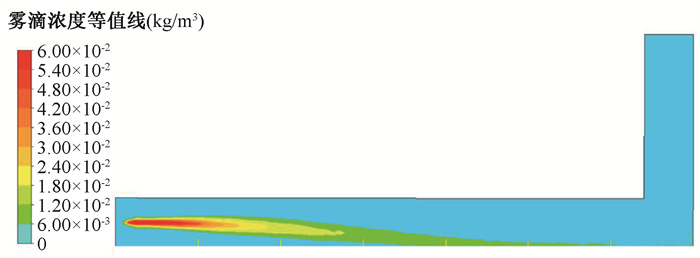
(3) 雾滴沉降量的模拟验证:单喷嘴工况下,底部沉降质量的模拟结果与实验结果的对比如表 2所示。从中可以看出,底部的沉降在总额上相当,但相比数值模拟,实验中雾滴沉降更为集中。这主要是由于数值模拟中微雾的曳力被高估了,导致雾滴的最大沉降点后移到了4~5 m之间,如图 4所示,而根据实验结果,雾滴的最大沉降点位于3 m附近。尽管最大沉降点存在差异,但是对沉降总量以及蒸发距离的影响较小,可用于后续工程设计多喷嘴条件下的数值模拟,且对于蒸发实效的验证更加保守。
|
|
表 2 实测雾滴沉降率与数值模拟结果对比(kg/h) Table 2 Comparison between measured droplet settling rates and numerical simulation results (kg/h) |
|
图 4 单喷嘴实验中高压喷雾雾滴载带进程的数值模拟 Figure 4 Simulation diagram of droplets-carrying process sprayed from a single high-pressure nozzle |
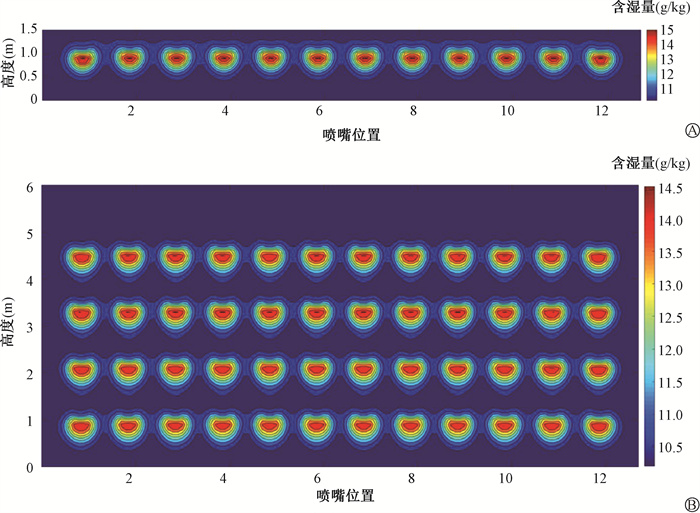
2. 多喷嘴蒸发实效的数值模拟:工程设计蒸发室为一个长方体的空间,其中,高压微雾喷嘴分多层布置,其中的每一层也均匀布置多排喷嘴同时水平喷射。仍采用ICEM对水平蒸发室进行网格划分,在x轴(来流法平面与水平面交线)方向网格间距为0.1 m,在y轴(来流方向)方向网格间距为0.2 m,在z轴(竖直方向)方向网格间距为0.25 m,合计452 374个网格。由于过高的粒子数目对计算的负担极大,且对于设计工况而言,最难蒸发,而又易于被底面捕捉的是最底层喷嘴释放的微雾;即若最底层的微雾能完全蒸发,则上层的微雾在来到下一层之前也能完全蒸发。为验证这一想法的可行性,将水平单层计算结果与多层喷嘴均开启的结果进行对比,取来流法向5.0 m处(第2排喷嘴前)截面,分别计算两种工况下全4层与最底层的含湿量,如图 5所示。
|
图 5 某典型工况下单层模拟与多层模拟的含湿量对比图 A.最底层喷嘴来流5 m截面处;B.4层喷嘴来流5 m截面处 Figure 5 Comparison of moisture contents between single-layer simulation and multi-layer simulation under a typical working condition A. At the cross-section of 5 meters from the bottom nozzles; B. At the cross-section of 5 meters from the 4-layer nozzles |
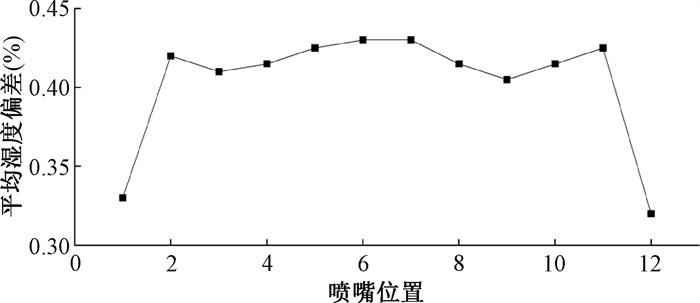
从中可以看出,对于多喷嘴的水平蒸发室,由于各喷嘴间的间距较大,特别是上下两层喷嘴间的距离较远,使得第1排喷嘴喷发的微雾在水平输运至第2排喷嘴前,在水平和竖直两个方向均几乎未受到来自其他喷嘴的影响,也不会发生沉降到下一层或底面的现象。比较全4层情况下最底层1.5 m的平均湿度与单层情况下湿度在水平方向的变化,以每个喷嘴的控制区域为中心对周围1 m区域进行平均,其结果如图 6所示,其偏差均在0.45%以内,因此,考虑计算量与数据有效性的平衡,以最底层来代表全4层的计算是可行的。
|
图 6 某典型工况下单层模拟与多层模拟最底层水平方向平均湿度偏差图 Figure 6 Diagram of average humidity deviation in the bottom horizontal direction between single-layer simulation and multi-layer simulation under a typical working condition |
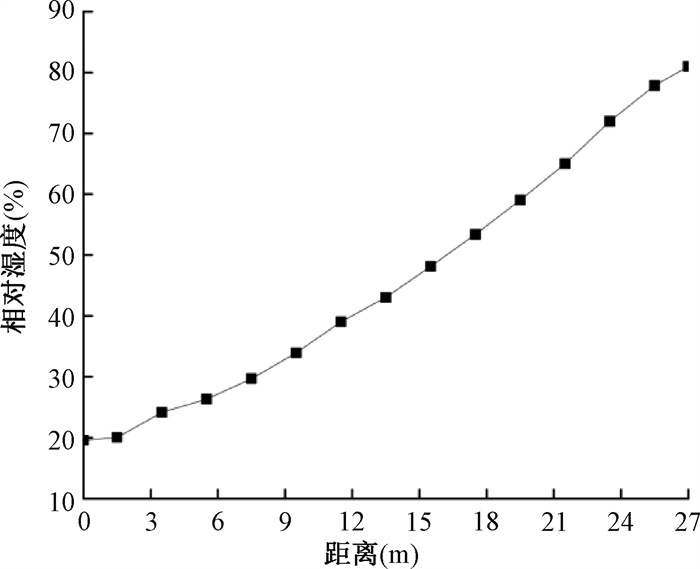
其中,最不利蒸发工况为来流温度28.74℃,来流含湿量5.0 g/kg,单个喷嘴流量2 g/s,载带流速1.28 m/s。此条件下的粒子追踪图如图 7所示,相对湿度随距离变化如图 8所示。从中可以看出,随着水平载带进程的增加,喷嘴数量及微雾数量逐步增加,导致水平蒸发室的相对湿度逐步增加,在出口附近已经达到81%,满足工艺设计要求达到80%左右的相对湿度要求。统计出口截面逃逸出去的粒子流量,用喷嘴流量减去逃逸出去的流量后再除以喷嘴流量,得到最不利工况下的蒸发百分比为99%。

|
图 7 实际蒸发室最不利工况下最底层喷嘴的粒子追踪图 Figure 7 Particle tracking diagram of the bottom nozzles in the actual evaporator under the hardest design condition |
|
图 8 最不利工况下相对湿度随距离变化 Figure 8 Relative humidity variation with distance under the hardest design condition |
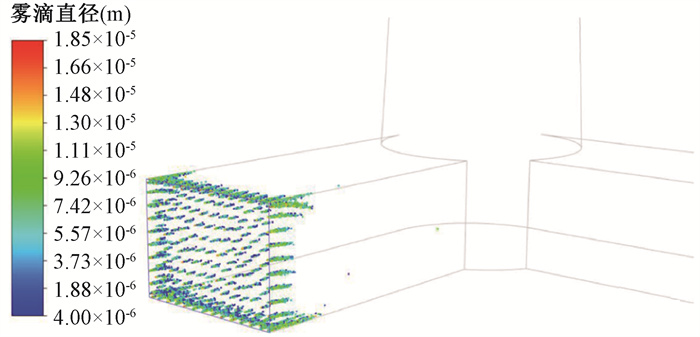
3. 微雾逃逸至竖直烟囱内的数值模拟:进一步以上述最不利工况做保守估计,将该工况下的出口截面和出口粒径分布作为进口条件,保守选取烟囱另一侧其他工艺废气的温度为20℃、相对湿度为60%,进行数值模拟,结果如图 9所示。从中可以看出,微雾在水平蒸发段出口很短的地方即几乎完全蒸发,仅有极个别的微雾能进入竖直烟囱段,但与较低湿度的气体混合后仍迅速蒸发。且由于混合气体的湿度距离饱和存在较大差距,离开烟囱后也不会发生冷凝。
|
图 9 微雾逃逸至竖直烟囱内的粒子追踪示意图 Figure 9 Particle tracking diagram of micro droplets escaping into the vertical chimney |
讨论
液态流出物排放是核能行业面临的一个重要问题,也是决定核设施厂址选择的关键因素。对于没有适当受纳水体的内陆厂址,采用大气载带的液转气排放方案,进而纳入气载流出物排放的管理范畴,是国内外普遍采用的工程实践,但尚未形成明确的技术路线。其中,最早的应用实践是采用天然蒸发池以自然蒸发的方式将液态流出物转化成气态排入大气,这一排放方案特别适用于降水量较小、蒸发量较大的核设施厂址。例如,位于美国亚利桑那州索诺兰沙漠盆地的Palo Verde核电厂利用天然蒸发池对液态流出物进行蒸发处理,可实现向地表水体的零排放,且对周围公众的辐射环境影响可忽略[19]。然而,天然蒸发池的蒸发效率较低,易受季节和天气因素影响,因而工程的占地面积往往较大,且需承受当地设计基准地震动,并做好防渗处理以及设置监测井等,因此,天然蒸发池的工程造价较高,且由于沙尘沉积,在运行过程会产生极低放射性固体废物。
与传统蒸发池的水平蒸发面相比,韩国研究堆1号和2号反应堆的去污和退役现场首次采用垂直挂布形成垂向蒸发液膜,同时,通过风机提供来自外部的空气以增加蒸发速率[20]。这种非沸腾强制蒸发载带的工艺流程简单、运行成本低,且技术可靠、运行效果良好,只是受限于挂布的蒸发面积及风机功率,挂布载带的蒸发效率虽高于天然蒸发池,但总体蒸发强度仍偏低,往往只适用于小型核设施和仅有少量液态流出物的液转气排放,且由于挂布是喷淋液态流出物的重要载体,需要经常更换,因此,在运行过程中也会产生放射性固体废物。
本研究通过高压雾化显著增大了蒸发面积,提高了蒸发强度,同时,显著减少了占地面积和工程施工量,不仅提高了自动化程度、节省工程造价,而且可以完全实现液转气排放,不额外产生放射性固体废物。此外,由于本研究的强制通风更加集中,可将载带后的气载流出物引入竖直烟囱实现高架排放,与天然蒸发池的地面面源蒸发排放相比,可显著降低近区的辐射环境影响[21]。本研究通过实验验证和数值模拟,论证了典型工艺设计条件下,净化后含氚废水经高压喷雾载带后,在离开烟囱出口时可以实现完全蒸发,进而在北方较干燥的大气环境下,可以气载流出物的形态在大气中输运和扩散,而不会发生聚并或冷凝为液滴而在厂址近区沉降,相关研究结论为揭示高压微雾在水平蒸发室和竖直烟囱段内的实际载带进程和蒸发特性提供了坚实的理论和数据支撑,为合理解决大型核设施液态流出物排放提供了一种新的解决思路。
需要说明的是,由于我国北方内陆厂址四季温差较大,高压微雾载带排放也需选择在合适的月份及天气条件下进行,由此会导致各月份载带气来流的温湿度特性发生变化,同时,也要求对烟囱出口处载带后气载流出物的温湿度特性进行限定。此外,实际工程设计中也会考虑用厂区排风来部分代替或全部代替新风进行载带,因此,整个工艺流程和运行参数是在动态调整和优化的。本研究只是从各月平均工况中选取最具代表性的最差工况进行举例论证,实际工程实践中应提前预判,选择合适的排放时间和技术手段,确保微雾在烟囱出口处实现完全蒸发。后续应针对各类工况进行更全面和精细化的模拟和验证,以不断积累和优化各类工况下的工艺参数,分析并提高载带强度,扩展该工艺的适用范围;同时,在工程实践前后应加强周边环境监测,用实测数据进一步验证高压微雾高架载带排放的可靠性,为我国今后更广范围地应用类似工艺提供有力的技术支撑和保障。
利益冲突 无
志谢 感谢中国核电工程有限公司武毓勇团队和上海交通大学王德忠团队的悉心指导和大力支持
作者贡献声明 王博负责实验设计与实施、论文撰写;吕彩霞负责文献调研及整理;廖运璇、张爱玲负责技术指导并提出修改建议
| [1] |
Liu L, Guo H, Dai LH, et al. The role of nuclear energy in the carbon neutrality goal[J]. Prog Nucl Energ, 2023, 162: 104772. DOI:10.1016/j.pnucene.2023.104772 |
| [2] |
Kim P, Yasmine H, Yim MS, et al. Challenges in nuclear energy adoption: why nuclear energy newcomer countries put nuclear power programs on hold? [J]. Nucl Eng Technol, 2023, ahead of print. DOI: 10.1016/j.net.2023.11.026.
|
| [3] |
杨德睿, 吴思远, 聂保杰, 等. 高压微雾蒸发排放低放废液数值模型与验证[J]. 核技术, 2023, 46(9): 57-65. Yang DR, Wu SY, Nie BJ, et al. Numerical modeling and validation for evaporation and discharge of low level radioactive wastewater based on high pressure spray technology[J]. Nucl Tech, 2023, 46(9): 57-65. DOI:10.11889/j.0253-3219.2023.hjs.46.090502 |
| [4] |
程卫亚, 陈连杰, 许慧萍, 等. 某设施净化后含氚废水生态排放环境影响研究[J]. 中国辐射卫生, 2020, 29(5): 550-554. Cheng WY, Chen LJ, Xu HP, et al. Study on environmental impact of ecological discharge of tritium-containing wastewater after purification in a facility[J]. Chin J Radiol Health, 2020, 29(5): 550-554. DOI:10.13491/j.issn.1004-714X.2020.05.026 |
| [5] |
López J, Pineda H, Bello D, et al. Study of liquid-gas two-phase flow in horizontal pipes using high speed filming and computational fluid dynamics[J]. Exp Therm Fluid Sci, 2016, 76: 126-134. DOI:10.1016/j.expthermflusci.2016.02.013 |
| [6] |
Aydin O, Unal R. Experimental and numerical modeling of the gas atomization nozzle for gas flow behavior[J]. Comput Fluids, 2011, 42(1): 37-43. DOI:10.1016/j.compfluid.2010.10.013 |
| [7] |
Wang CC, Prather KA, Sznitman J, et al. Airborne transmission of respiratory viruses[J]. Science, 2021, 373(6558): eabd9149. DOI:10.1126/science.abd9149 |
| [8] |
Barrow H, Pope CW. Droplet evaporation with reference to the effectiveness of water-mist cooling[J]. Appl Energ, 2007, 84(4): 404-412. DOI:10.1016/j.apenergy.2006.09.007 |
| [9] |
Huang C, Cai J, Lin Z, et al. Solving model of temperature and humidity profiles in spray cooling zone[J]. Build Environ, 2017, 123: 189-199. DOI:10.1016/j.buildenv.2017.06.043 |
| [10] |
Lock JA, Gouesbet G. Generalized Lorenz-Mie theory and applications[J]. J Quant Spectrosc Ra, 2009, 110(11): 800-807. DOI:10.1016/j.jqsrt.2008.11.013 |
| [11] |
Antonov D, Fedorenko R, Strizhak P, et al. A simple model of heating and evaporation of droplets on a superhydrophobic surface[J]. Int J Heat Mass Tran, 2023, 201: 123568. DOI:10.1016/j.ijheatmasstransfer.2022.123568 |
| [12] |
Li S, Zhao B, Lin H, et al. Review and prospects of surfactant-enhanced spray dust suppression: mechanisms and effectiveness[J]. Process Saf Environ, 2021, 154: 410-424. DOI:10.1016/j.psep.2021.08.037 |
| [13] |
Gavhane S, Pati S, Som SK. Evaporation of multicomponent liquid fuel droplets: influences of component composition in droplet and vapor concentration in free stream ambience[J]. Int J Therm Sci, 2016, 105: 83-95. DOI:10.1016/j.ijthermalsci.2016.03.003 |
| [14] |
Sazhin S. Droplets and sprays[M]. London: Springer, 2014. DOI:10.1007/978-1-4471-6386-2
|
| [15] |
Liu CY, Nie W, Hua Y, et al. The migration of CO and PM under different working conditions of trackless rubber-tyred vehicle and health risk assessment of underground personnel[J]. Chemosphere, 2022, 307: 135750. DOI:10.1016/j.chemosphere.2022.135750 |
| [16] |
Shuvo S, Sakib N, Rahman R, et al. Particle deposition and characteristics of turbulent flow in converging and diverging nozzles using Eulerian-Lagrangian approach[J]. Results Eng, 2022, 16: 100669. DOI:10.1016/j.rineng.2022.100669 |
| [17] |
Morsi S, Alexander A. Investigation of particle trajectories in 2-phase flow systems[J]. J Fluid Mech, 1972, 55: 193-208. DOI:10.1017/S0022112072001806 |
| [18] |
Roberts J, Wypych P, Hastie D, et al. Analysis and validation of a CFD-DPM method for simulating dust suppression sprays[J]. Part Sci Technol, 2022, 40(4): 415-426. DOI:10.1080/02726351.2021.1951907 |
| [19] |
United States Nuclear Regulatory Commission. Generic environmental impact statement for license renewal of nuclear plants (NUREG-1437). Supplement 43, regarding Palo Verde nuclear generating station. Final report[R]. Rockville, Maryland: USNRC, 2011. www.nrc.gov/docs/ML1035/ML103560149.pdf.
|
| [20] |
Jung KJ, Lee KW, Lee DG, et al. Evaluation of the discharged radioactivity during the concentration of the very low-level liquid radioactive waste (VLLW) by a natural evaporator at the KRR-1&2 site. Proceedings of the Korean Nuclear Society Conference, 2004 Korean Nuclear Society Autumn Meeting[C]. Pyeongchang: Korean Nuclear Society, 1275-1276. www.koreascience.or.kr/article/CFKO200436025565856.pdf.
|
| [21] |
刘新华, 邓治国, 张志银, 等. 内陆核电厂液态流出物液转气排放可行性初探[J]. 核科学与工程, 2020, 40(3): 450-457. Liu XH, Deng ZG, Zhang ZY, et al. Study on the feasibility of liquid-to-gas conversion discharge of effluent from inland nuclear power plants[J]. Nucl Sci Eng, 2020, 40(3): 450-457. DOI:10.3969/j.issn.0258-0918.2020.03.015 |
 2024, Vol. 44
2024, Vol. 44


