2. 首都医科大学附属北京同仁医院放射科, 北京 100730
2. Department of Radiology, Beijing Tongren Hospital, Capital Medical University, Beijing 100730, China
目前, 全国约有7.53万家放射诊疗机构, 每年开展的放射诊疗操作近10亿人次,为患者健康做出了巨大贡献,但同时也产生了不可忽略的电离辐射风险[1]。我国2016年接受放射诊断总人次约7.82亿,其中常规X射线检查占52.4%,CT检查占37.1%,介入放射学占0.7%,核医学为1.1%[2]。美国CT检查人次数较十年前增长了25% (约8 400万人次) [3]。联合国原子辐射效应科学委员会(UNSCEAR) 发布的2020/2021报告显示,在所有放射诊断成像中,CT检查对集体有效剂量贡献高达61.6%[4]。在对26个国家320万患者的CT辐射剂量调查中发现,全球每年约有90万患者接受CT辐射剂量超过100 mSv[5]。在乳腺癌早期筛查中,放射诊断在提高检出率的同时也会增加女性患癌风险[6]。国际放射防护委员会(ICRP) 103号报告[7]将乳腺的组织权重因子从0.05调整到0.12,说明乳腺X射线摄影的电离辐射风险也在逐渐升高。介入放射诊疗的人次数占比仅为0.6%, 但对集体有效剂量的贡献可达8%[4]。因此, 放射诊断过程中的剂量评估是临床研究的一个重要内容。蒙特卡罗模拟作为一种重要的计算机随机模拟方法, 已经被广泛应用于放射诊断的剂量估算、成像优化、系统设计及辐射防护等多个场景。本文对蒙特卡罗模拟及其在放射诊断不同成像技术中剂量估算的研究概况进行综述。
一、蒙特卡罗方法的原理蒙特卡罗(Monte Carlo) 方法最早由乌拉姆和冯·诺依曼在1940年提出, 该名称来自摩纳哥世界著名赌城Monte Carlo。蒙特卡罗方法的基本思想是当所求问题的解为某件事情的概率或某个随机变量的数学期望或与两者相关的某变量时, 通过某种试验的方法得到该事件发生的频率, 通过它得到问题的解[8]。为了得到足够精确的近似解, 试验的次数必须要足够多, 通过人工的方法实现较为困难。随着计算机的出现,可以把大量重复性的实验交给计算机来完成, 极大降低了蒙特卡罗方法的复杂性, 使其得到广泛应用。蒙特卡罗方法可以精确地模拟放射线在人体内部的传输和散射过程, 从而得到人体内部的剂量分布和解剖信息。
蒙特卡罗模拟的实现过程包括源分布抽样、源粒子能量抽样、源粒子运动方向抽样、碰撞点位置处理、碰撞后能量随机抽样、碰撞后散射角的随机抽样以及碰撞后运动方向的确定。这些过程的计算和处理非常复杂, 但往往只需实现一次即可。为了避免重复且复杂的计算工作, 许多不同的蒙特卡罗程序被设计开发出来, 这些程序一般都具有非常丰富的截面库和物理过程, 极大方便了蒙特卡罗模拟在各个领域的应用, 表 1总结了常用的不同蒙特卡罗模拟程序的特点[9]。
|
|
表 1 不同蒙特卡罗程序的对比 Table 1 Comparison of different Monte Carlo codes |
1. Geant4/GATE(Geant4 application for tomographic emission): Geant4是一个基于C++开发的蒙特卡罗应用程序, 由欧洲原子能机构开发并用于模拟粒子与物质相互作用。Geant4中有丰富的物理过程截面库, 涉及光子、中子、电子、质子以及重离子等多种辐射粒子, 具有良好的通用性和扩展能力[10-11]。目前基于Geant4开发的程序有Geant4-DNA、GAMOS、GATE、GHOST、TOPAS等, 其中GATE是基于Geant4开发的专门用于医学影像和放射治疗的模拟程序[12]。GATE以宏命令的格式执行程序, 不需要用户具有C++编程的基础, 极大降低了使用的难度。
2. MCNP(Monte Carlo N-particle transport code system): MCNP是由美国Los Alamos National Laboratory开发的一套模拟中子、光子和电子在物质中输运过程的通用蒙特卡罗计算程序, 其通过曲面卡和栅元卡对几何模型进行描述。MCNP的通用性强, 方差减小技巧比较全面。与Geant4相比, MCNP输入项中材料的几何设置较为方便, 但模拟粒子的能量范围较小。
3. EGS (electron-gamma shower):由美国斯坦福直线加速器中心(SLAC) 和加拿大国家研究所(NRCC) 联合推出的一款用于模拟光子和电子输运的蒙特卡罗程序。EGS最初是为了研究高能物理领域的问题而开发的, 后来逐渐在辐射物理和医学物理等方面得到了广泛的应用。
Geant4、MCNP以及EGS等软件功能非常强大, 但同时使用难度较高。为了降低其使用复杂性, 一些操作简单的蒙特卡罗模拟软件(例如ImpactDose、PCXMC和ImPACT 2.0) 内置了不同的计算体模, 用户只需手动设置扫描参数即可完成模拟, 极大地便利了蒙特卡罗模拟在临床上的开展。然而, 这些软件使用的体模大都以欧美人群为标准, 不符合中国人的生理特征, 模拟结果存在较大偏差。清华大学研究团队建立了多尺度的中国参考人体模, 并将模拟得到的数据集成于一个基于Web的剂量评估软件中[13]。
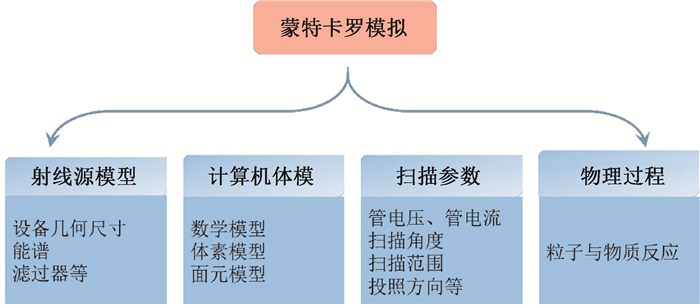
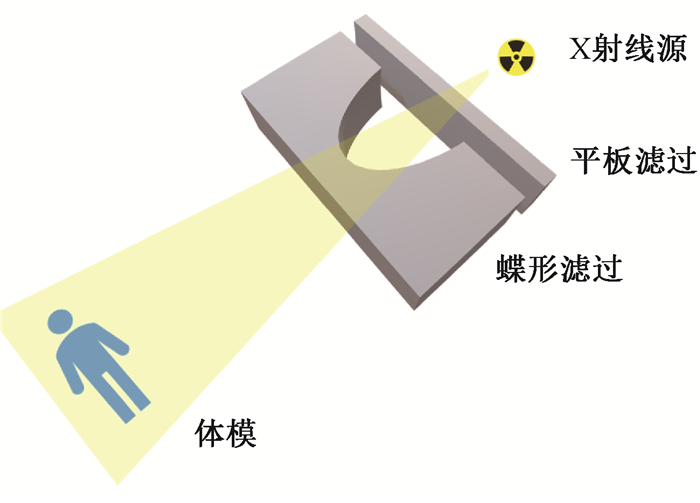
二、蒙特卡罗模拟的建模过程图 1描述了蒙特卡罗模拟的建模过程, 主要包括发射源模型建模、计算机仿真体模建模、扫描参数建模和物理过程建模[14], 这些建模过程与模拟计算结果的精度密切相关。以CT设备为例, 发射源模型包括CT的几何尺寸、能谱以及滤过器等。能谱可由相应的软件生成(如XCOMP5R[15]、SpekCalc[16]和Spektr[17]等)。图 2展示了CT扫描的简易模型, 由于射线束具有多色性, 在进行诊断扫描时需要调整射线束能谱分布, 选择合适的平板滤过和蝶形滤过可以吸收低能射线并产生均匀的射线分布。计算机体模是指在模拟过程中用来替代受检者的模型, 它能够模拟真实受检者在接受射线束之后产生的能量吸收情况, 关于计算机仿真体模的研究进展将在第三节详细介绍。模拟过程中的扫描参数主要包括管电流、管电压、扫描射野范围、射线束扫描角度以及投照方向等。物理过程指在模拟过程中粒子与物质发生的反应, 用户需要选择与研究目的相关的物理反应, 常用的物理过程可由Geant4和MCNP等程序建立。
|
图 1 蒙特卡罗模拟建模过程 Figure 1 The modeling process of Monte Carlo simulation |
|
图 2 CT扫描简易模型 Figure 2 The simple model of CT scan |
三、计算机仿真体模
计算机仿真体模的设计过程主要包括从影像中提取器官轮廓、特殊器官构建、器官优化调整、器官材料填充以及器官的组合[13, 18]。器官轮廓可以通过手动勾画或半自动分割来获取。近年来, 随着人工智能技术发展迅速, 也有研究使用深度学习的方法实现了全自动器官分割[19], 极大缩短了获取器官轮廓的时间。对于一些特殊的器官或组织如皮肤、小肠、结肠、眼晶状体等需要手动构建。人体的器官一般来说比较复杂且不规则, 在构建器官时需要借助一些3D建模软件如CAD和Rhinoceros等进行微调, 以适应大多数患者的解剖和生理数据[20]。
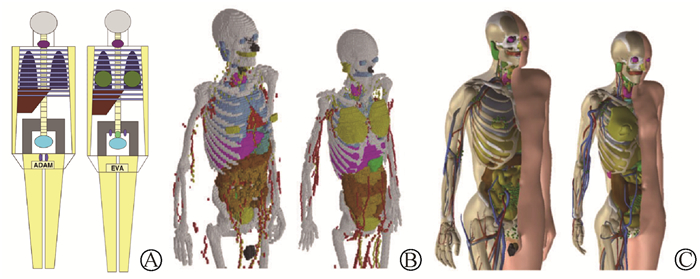
蒙特卡罗模拟使用的计算体模主要分为数学模型、体素模型和面元模型(图 3)。其中, 数学模型是把人体组织或器官简化成可以用数学描述的几何形状, 由于其对器官进行了大量的简化, 其精度较低。体素模型随着CT技术的发展应运而生, 该模型是把人体划分成几百万甚至上亿个体素。根据组织或器官组成成分的不同, 每个体素有不同的性质。体素模型由于以真实患者影像为基础, 其相比数学模型更加真实, 在模拟剂量计算中逐步取代数学模型的应用。然而体素模型的表面可能会产生阶梯状分布, 在细节及复杂的区域塑造上精度较差[21]。面元模型是指通过利用平滑曲面如非均匀有理样条曲面(NURBS) 或多边形网格(polygon mesh, PM) 来表示人体器官轮廓的方法建立的仿真人体模型。面元模型的质量和精度取决于网格的密度及分布, 其表面相对较为光滑, 更能展现人体的细节。
|
A. 数学模型;B. 体素模型[22];C. 面元模型[23] 图 3 用于蒙特卡罗模拟的不同模型 A. Mathematical phantom; B. Voxel phantom[22]; C. Mesh phantom[23] Figure 3 Different phantoms used for Monte Carlo simulations |
目前已有的标准化人体计算模型包括ICRP 110[22]和ICRP 145[23]报告提供的标准体模、MASH3/FASH3[24]、Rensselaer理工学院(RPI) 成年人体模[25]等。然而符合中国参考人的体模相对较少。随后, Ma等[20]建立了中国儿童参考人面元模型, 包括3个月、1、5、10和15岁的儿童, 体模包括85个器官, 经过优化和调整, 各组织和器官质量与亚洲参考人的参考值差异 < 1%, 各器官的形态特点基本符合中国儿童的解剖学特征, 这对儿童诊断剂量研究具有重要意义。此外, 还有其他相关研究也分别建立了中国成年人及儿童参考体模[26-28]。虽然标准参考体模可以反映平均的放射诊断剂量水平, 但标准化的参考体模不能精准地反映个体化患者受到的剂量。Xie等[29]通过对特定患者的CT图像进行器官分割, 生成了表示个体化患者的区域体素模型, 将得到的区域体素模型与之前建立的体模库进行匹配从而选择出与该患者体型最接近的体模, 该患者的完整体素模型通过对标准体模缩放得到。
四、蒙特卡罗模拟在放射诊断剂量估算中的应用放射诊断领域常用的X射线成像设备包括X射线摄影、计算机体层X射线成像、乳腺X射线摄影和介入诊疗等。这些检查中患者会接受一定量的X射线辐射, 但精确评估患者所接受的辐射剂量有一定困难。蒙特卡罗方法依靠计算机进行模拟计算, 具有很高的精确性, 在临床上已经广泛应用于各种放射诊断技术的剂量评估和成像优化中。
1. 蒙特卡罗模拟在X射线摄影中的应用:医疗照射中, X射线摄影的频次占比最大[1]。蒙特卡罗模拟可用于评估X射线诊断过程中人体组织或器官受到的照射水平, 从而有效监测受检者的辐射剂量。X射线摄影中常用入射体表剂量来估算受检者的器官剂量和有效剂量。刘倩倩等[30]利用蒙特卡罗模拟计算了常见X射线摄影不同照射位置下器官剂量转换系数, 研究表明使用不同模型模拟得到的器官剂量转换系数偏差可达50%以上, 使用体素模型可以得到更加精确的结果。马锐垚等[31]基于中国儿童面元模型评估了X射线摄影中的剂量水平, 并得到了器官剂量与有效剂量转换系数的数据库, 其研究结果为中国儿童临床X射线摄影剂量评估提供了更为精确的参考数据。此外, 蒙特卡罗方法还可用于研究成像质量和患者剂量间的平衡问题。李师等[32]通过组合不同管电压及滤过厚度来模拟双能X射线吸收法腰椎成像过程的成像参数, 研究发现当低能管电压为70 ~ 85 kVp, 高能管电压为160 ~ 200 kVp,过滤铜厚度为0.3 mm时, 可以在获得较好图像质量的同时尽可能降低患者的辐射剂量。
2. 蒙特卡罗模拟在CT检查中的应用:CT检查在放射诊断中使用范围广、频率高, 多次扫描的累积剂量给患者带来了巨大的潜在风险, 而蒙特卡罗模拟具有成本低而且精度高的特点, 是评估CT扫描辐射剂量的理想工具。在CT检查器官剂量估算中, 蒙特卡罗模拟的显著优势是可以直接根据CT图像进行模拟计算得到受检者的剂量分布。这是因为CT成像的本质是衰减系数成像, CT值可以反映出体模的密度和元素组成信息[33]。根据CT断层成像的特点, 潘羽晞等[34]根据CT图像构建了1岁儿童体素模型, 模拟计算了CT检查过程中儿童受到的剂量水平, 并通过放置在体模内的TLD进行测量验证, 最终建立了CT单层轴向扫描时对1岁儿童36个器官或组织所产生医疗照射剂量的数据库, 与测量值相比, 利用该数据库估算的剂量偏差在25%以内。Xie等[35]根据CT图像设计了一个孕妇模型, 使用蒙特卡罗的方法模拟CT检查, 研究表明妊娠期女性患者接受CT检查很大程度上会导致胎儿受到过量的照射。蒙特卡罗方法还可用于改善CT检查中的辐射剂量, Huang等[36]和Yang等[37]通过蒙特卡罗模拟来验证基于器官管电流调制(tube current modulation, TCM) 技术在减少眼晶状体剂量和胸部扫描器官剂量的效果。模拟得到的剂量分布可以用来优化TCM技术的扫描参数, 以保证重要器官或组织受到较小的辐射剂量。研究表明, TCM技术能够将眼晶状体剂量减少47%以上。
3. 蒙特卡罗模拟在乳腺X射线摄影中的应用:乳腺X射线摄影是筛查乳腺癌的重要措施, 然而其带来的辐射也存在潜在的风险, 通常由平均腺体剂量(mean glandular dose, MGD) 来评估乳腺组织的平均吸收剂量。MGD可以通过在视野固定区域测得的空气比释动能K与归一化腺体剂量系数(normalized glandular dose coefficients, DgN) 乘积得到。DgN与腺体含量、乳腺解剖结构和X射线能谱有关[38]。在乳腺X射线摄影剂量计算中, 大多数研究采用均匀的乳房模型, 而腺体在乳房内实际呈不均匀分布, 均匀模型所得的结果误差较大。王文静等[39]基于不同患者皮肤和脂肪厚度设计了一种精细化的乳房模型进行剂量评估, 该模型具有皮肤、皮下脂肪、乳房后侧脂肪、悬吊韧带、纤维腺体区脂肪、输乳管、小叶、输乳窦和乳头等精细结构。之后, Wang等[40-41]基于此精细乳房模型,模拟计算了乳腺X射线摄影过程乳房内的剂量分布, 得到了不同腺体含量、不同压迫厚度、不同管电压及不同滤过组合下的一系列DgN。与简单的均匀模型相比, 使用精细乳房模型计算的剂量偏差可达5.4%~38.0%。此外, Chang等[42]还设计了一种具有3层结构的混合乳房模型, 其每一层可以设置不同的腺体含量, 该模型可以更精确地建模不同腺体分布的人群。
4. 蒙特卡罗模拟在介入诊疗中的应用:介入放射诊断和治疗中, 患者和医务人员的剂量评估和辐射防护一直是放射诊断领域内的重要研究内容。李孟阳等[43]通过蒙特卡罗模拟建模了冠状动脉介入术的辐射场景, 计算了介入诊疗过程中剂量面积乘积分别与肺、骨髓、肝脏及心脏的器官吸收剂量的转换系数, 为临床上快速评估冠状动脉介入术中患者的器官剂量提供了便利。王遥等[44]基于蒙特卡罗模拟计算了医生在肝动脉化疗栓塞手术中不同站姿以及佩戴铅眼镜对眼晶状体的辐射防护效果, 研究表明,右转45°站姿和佩戴铅眼镜可以有效保护医务人员的安全。Bhar等[45]使用蒙特卡罗模拟评估了介入心脏病学手术中患者和医务人员在不同位置受到的辐射水平。其中, 手术主操作者相比其他位置的医务人员受到的剂量最大, 应给予更加有效的防护措施。因此, 该研究同时为手术主操作者设计了一种新型的辐射防护舱, 并与常规辐射防护措施进行比较。研究表明, 这种新型辐射防护设施可以使医生受到的器官剂量平均减少83.88%, 从而进一步保证医务人员的生命健康。
五、蒙特卡罗模拟的局限蒙特卡罗模拟是放射诊断领域剂量估算的重要研究方法, 其广泛应用于各种放射性成像技术的剂量估算中。为了追求更加精确的剂量评估, 计算机仿真体模经过了由数学模型到体素模型, 再到面元模型的发展过程, 在高精度体模上模拟计算得到的数据库也使得剂量的快速估算变得更加精确。然而, 蒙特卡罗模拟还存在一些问题需要解决。
首先, 影响蒙特卡罗模拟开展最主要的是其计算速度问题, 根据模拟粒子数量及计算机体模复杂度的差异, 完成一次模拟往往需要耗费几小时甚至几天的时间。为了加快模拟的速度, 多线程技术被广泛应用。其原理是蒙特卡罗模拟中每个粒子被视为相互独立的, 因此可以将模拟的粒子数目分给多个线程同时处理, 最后将每个线程得到的结果累加。然而, CPU的计算速度毕竟很有限。目前有很多基于GPU计算的方法被提出来以加快蒙特卡罗的模拟, 其计算速度相比CPU可以快6.7~11.4倍[46-49]。由此可见, GPU加速的蒙特卡罗模拟是解决其计算速度问题最有效的途径之一。
其次, 蒙特卡罗模拟的精度非常依赖对扫描设备和计算机体模的精确建模。对于CT设备建模来讲, X射线的能谱及其滤过是其最重要的参数, 而这些参数一般是设备厂家独有的。因此, 实现对扫描设备的精确建模也很困难。但可以借助探测器阵列测量及计算的方式来间接分析滤过器的形状[50-53], 或使用能谱估计的方法直接估计X射线在经过滤过器后的能谱[54-56]。目前已有许多的计算机体模被设计出来包括各种标准化体模和个体化体模, 有效提升了蒙特卡罗模拟的精度。但用于蒙特卡罗模拟的现有计算体模大多是静态的, 没有考虑器官的自主运动如呼吸运动、心脏搏动和肠道蠕动等因素, 这些运动在一定程度上也会影响对器官剂量评估的准确性, 但关于动态计算机仿真体模的研究少有开展。因此, 精确的放射检查设备建模及动态计算机体模建模是改善蒙特卡罗模拟精度的重要途径。
六、结语放射诊断中的剂量估算及辐射防护是临床上的一个重要问题, 蒙特卡罗模拟凭借其强大的计算机仿真能力, 可以精确地评估患者在放射检查中受到的剂量。临床上可以根据模拟得到的剂量分布来进一步优化放射检查操作。本文对蒙特卡罗模拟的原理、建模过程及其在放射诊断剂量估算上的应用进行了综述。总之, 蒙特卡罗模拟在放射诊断剂量估算中的应用非常广泛, 该方法对患者和放射工作人员的受照剂量估算具有重要的价值。在未来, 蒙特卡罗模拟的GPU加速、成像技术或成像参数优化以及计算机仿真体模的精准构建将是重要的研究内容。随着技术的进步和研究的深入, 蒙特卡罗模拟在放射诊断剂量估算和优化中将具有更广阔的应用空间。
利益冲突 无
作者贡献声明 张治杰负责文献调研和论文撰写;牛延涛指导论文撰写和修改;竺礼华、孙保华协助修改论文
| [1] |
牛延涛, 张永县, 卓维海, 等. 加强放射诊断辐射剂量管理的必要性及应对策略[J]. 中华放射医学与防护杂志, 2023, 43(4): 241-247. Niu YT, Zhang YX, Zhuo WH, et al. The necessity and countermeasures of strengthening radiation dose management in diagnostic radiology[J]. Chin J Radiol Med Prot, 2023, 43(4): 241-247. DOI:10.3760/cma.j.cn112271-20221205-00469 |
| [2] |
牛亚婷, 苏垠平, 梁婧, 等. 全国医疗照射频度估算方法研究[J]. 中华放射医学与防护杂志, 2019, 39(5): 325-330. Niu YT, Su YP, Liang J, et al. Study on estimation of medical exposure frequency in China[J]. Chin J Radiol Med Prot, 2019, 39(5): 325-330. DOI:10.3760/cma.j.issn.0254-5098.2019.05.002 |
| [3] |
Damilakis J. CT Dosimetry: What has been achieved and what remains to be done[J]. Invest Radiol, 2021, 56(1): 62-68. DOI:10.1097/RLI.0000000000000727 |
| [4] |
United Nations Scientific Committee on the Effects of Atomic Radiation. UNSCEAR 2020/2021 report. Evaluation of medical exposures to ionizing radiation[R]. New York: UNSCEAR, 2022.
|
| [5] |
Rehani MM, Yang K, Melick ER, et al. Patients undergoing recurrent CT scans: assessing the magnitude[J]. Eur Radiol, 2020, 30(4): 1828-1836. DOI:10.1007/s00330-019-06523-y |
| [6] |
薛珂, 徐辉, 岳保荣, 等. 乳腺X射线摄影中受检者辐射剂量评估研究进展[J]. 中华放射医学与防护杂志, 2023, 43(8): 663-668. Xue K, Xu H, Yue BR, et al. Research progress in the average glandular dose during mammography[J]. Chin J Radiol Med Prot, 2023, 43(8): 663-668. DOI:10.3760/cma.j.cn112271-20230301-00057 |
| [7] |
International Commission on Radiological Protection. ICRP Publication 103. The 2007 recommendations of the International Commission on Radiological Protection[R]. Oxford: Pergamon Press, 2007.
|
| [8] |
许淑艳. 蒙特卡罗方法在实验核物理中的应用[M]. 北京: 原子能出版社, 2006. Xu SY. Application of Monte Carlo methods to experimental nuclear physics[M]. Beijing: Atomic Energy Press, 2006. |
| [9] |
王楚胭, 卓维海, 林鑫, 等. CT所致受检者个体化器官剂量的研究进展[J]. 中国辐射卫生, 2022, 31(6): 756-762. Wang CY, Zhuo WH, Lin X, et al. Research progress of patient-specific organ doses from CT[J]. Chin J Radiol Health, 2022, 31(6): 756-762. DOI:10.13491/j.issn.1004-714X.2022.06.021 |
| [10] |
Allison J, Amako K, Apostolakis J, et al. Geant4 developments and applications[J]. IEEE Trans Nucl Sci, 2006, 53(1): 270-278. DOI:10.1109/TNS.2006.869826 |
| [11] |
Agostinelli S, Allison J, Amako K, et al. Geant4-a simulation toolkit[J]. Nucl Instrum Methods Phys Res(Section A), 2003, 506(3): 250-303. DOI:10.1016/S0168-9002(03)01368-8 |
| [12] |
Sarrut D, Bała M, Bardiès M, et al. Advanced Monte Carlo simulations of emission tomography imaging systems with GATE[J]. Phys Med Biol, 2021, 66(10): 10T. DOI:10.1088/1361-6560/abf276 |
| [13] |
任丽, 邱睿, 武祯, 等. 基于中国参考人的典型CT扫描患者剂量模拟与分析[J]. 中华放射医学与防护杂志, 2018, 38(12): 942-948. Ren L, Qiu R, Wu Z, et al. Simulation and analysis of CT examination doses to typical patients based on Chinese reference human phantoms[J]. Chin J Radiol Med Prot, 2018, 38(12): 942-948. DOI:10.3760/cma.j.issn.0254-5098.2018.12.012 |
| [14] |
Akhavanallaf A, Xie T, Zaidi H. Assessment of uncertainties associated with Monte Carlo-based personalized dosimetry in clinical CT examinations[J]. Phys Med Biol, 2020, 65(4): 045008. DOI:10.1088/1361-6560/ab6b45 |
| [15] |
Nowotny R, Höfer A. Program for calculating diagnostic X-ray spectra[J]. Rofo, 1985, 142(6): 685-689. DOI:10.1055/s-2008-1052738 |
| [16] |
Poludniowski G, Landry G, DeBlois F, et al. SpekCalc: a program to calculate photon spectra from tungsten anode X-ray tubes[J]. Phys Med Biol, 2009, 54(19): N433-438. DOI:10.1088/0031-9155/54/19/N01 |
| [17] |
Punnoose J, Xu J, Sisniega A, et al. Technical note: spektr 3.0-A computational tool for x-ray spectrum modeling and analysis[J]. Med Phys, 2016, 43(8): 4711. DOI:10.1118/1.4955438 |
| [18] |
潘羽晞, 邱睿, 刘立业, 等. 辐射防护用中国参考人体素模型建立、应用及最新进展[J]. 辐射防护, 2014, 34(4): 199-205. Pan YX, Qiu R, Liu LY, et al. Chinese reference human voxel phantoms for radiation protection: development application and recent progress[J]. Radiat Prot, 2014, 34(4): 199-205. |
| [19] |
Xie T, Zaidi H. Estimation of the radiation dose in pregnancy: an automated patient-specific model using convolutional neural networks[J]. Eur Radiol, 2019, 29(12): 6805-6815. DOI:10.1007/s00330-019-06296-4 |
| [20] |
Ma RY, Qiu R, Wu Z, et al. Development of Chinese mesh-type pediatric reference phantom series and application in dose assessment of Chinese undergoing computed tomography scanning[J]. Phys Med Biol, 2021, 66(19): 195002. DOI:10.1088/1361-6560/ac1ef1 |
| [21] |
葛朝永. 中国辐射防护参考人变形技术及应用研究[D]. 北京: 清华大学, 2014. Ge CY. Research on deformation technology and application of Chinese radiation protection reference man[D]. Beijing: Tsinghua University, 2014. |
| [22] |
International Commission on Radiological Protection. ICRP Publication 110. Adult reference computational phantoms[R]. Oxford: Pergamon Press, 2009.
|
| [23] |
International Commission on Radiological Protection. ICRP Publication 145. Adult mesh-type reference computational phantoms[R]. Oxford: Pergamon Press, 2020.
|
| [24] |
Cassola VF, Lima VJ, Kramer R, et al. FASH and MASH: female and male adult human phantoms based on polygon mesh surfaces: Ⅰ. Development of the anatomy[J]. Phys Med Biol, 2019, 55(1): 133. DOI:10.1088/0031-9155/55/1/009 |
| [25] |
Zhang J, Na YH, Caracappa PF, et al. RPI-AM and RPI-AF, a pair of mesh-based, size-adjustable adult male and female computational phantoms using ICRP-89 parameters and their calculations for organ doses from monoenergetic photon beams[J]. Phys Med Biol, 2009, 54(19): 5885-5908. DOI:10.1088/0031-9155/54/19/015 |
| [26] |
胡安康, 邱睿, 代明亮, 等. 10岁中国儿童参考人面元体模的建立[J]. 原子能科学技术, 2019, 53(1): 187-192. Hu AK, Qiu R, Dai ML, et al. Development of 10-year-old Chinese Pediatric reference boundary representation phantom[J]. At Energy Sci Technol, 2019, 53(1): 187-192. DOI:10.7538/yzk.2018.youxian.0161 |
| [27] |
汤晓斌, 耿长冉, 谢芹, 等. 基于NHMAN辐射仿真人体模型的蒙特卡罗方法剂量计算研究[J]. 中国医学物理学杂志, 2012, 29(2): 3216-3220. Tang XB, Geng CR, Xie Q, et al. The study of Monte Carlo dosimetry calculation based on nhman radiation human phantom[J]. Chin J Med Phys, 2012, 29(2): 3216-3220. DOI:10.3969/j.issn.1005-202X.2012.02.002 |
| [28] |
Pan Y, Qiu R, Gao L, et al. Development of 1-year-old computational phantom and calculation of organ doses during CT scans using Monte Carlo simulation[J]. Phys Med Biol, 2014, 59(18): 5243-5260. DOI:10.1088/0031-9155/59/18/5243 |
| [29] |
Xie T, Akhavanallaf A, Zaidi H. Construction of patient-specific computational models for organ dose estimation in radiological imaging[J]. Med Phys, 2019, 46(5): 2403-2411. DOI:10.1002/mp.13471 |
| [30] |
刘倩倩, 卓维海, 胡盼盼, 等. X射线摄影所致受检者器官剂量-入射体表剂量转换系数的研究[J]. 中华放射医学与防护杂志, 2015, 35(11): 871-874. Liu QQ, Zhuo WH, Hu PP, et al. Estimation of patient radiation doses form conventional X-ray radiography[J]. Chin J Radiol Med Prot, 2015, 35(11): 871-874. DOI:10.3760/cma.j.issn.0254-5098.2015.11.019 |
| [31] |
马锐垚, 邱睿, 任丽, 等. 基于中国儿童参考体模的X射线摄影剂量评估[J]. 中华放射医学与防护杂志, 2021, 41(5): 363-367. Ma RY, Qiu R, Ren L, et al. Dose estimation of X-ray radiography based on Chinese pediatric reference phantoms[J]. Chin J Radiol Med Prot, 2021, 41(5): 363-367. DOI:10.3760/cma.j.issn.0254-5098.2021.05.008 |
| [32] |
李师, 皮一飞, 霍万里, 等. 基于蒙特卡罗和CT数据体素模型的双能X射线吸收法腰椎骨密度成像参数优化[J]. 中华放射医学与防护杂志, 2018, 38(7): 541-546. Li S, Pi YF, Huo WL, et al. Optimization of DXA lumber spine bone imaging parameters based on Monte Carlo method and CT voxel phantom[J]. Chin J Radiol Med Prot, 2018, 38(4): 541-546. DOI:10.3760/cma.j.issn.0254-5098.2018.07.011 |
| [33] |
Schneider W, Bortfeld T, Schlegel W. Correlation between CT numbers and tissue parameters needed for Monte Carlo simulations of clinical dose distributions[J]. Phys Med Biol, 2000, 45(2): 459-478. DOI:10.1088/0031-9155/45/2/314 |
| [34] |
潘羽晞, 邱睿, 郑钧正, 等. 利用蒙特卡罗建模及估算儿童X-CT检查受照剂量[J]. 辐射防护, 2016, 36(3): 129-134. Pan YX, Qiu R, Zheng JZ, et al. Modeling and dose estimation of pediatric X-CT examination using Monte Carlo technique[J]. Radiat Prot, 2016, 36(3): 129-134. |
| [35] |
Xie T, Poletti PA, Platon A, et al. Assessment of CT dose to the fetus and pregnant female patient using patient-specific computational models[J]. Eur Radiol, 2018, 28(3): 1054-1065. DOI:10.1007/s00330-017-5000-z |
| [36] |
Huang Y, Zhuo W, Gao Y, et al. Monte Carlo simulation of eye lens dose reduction from CT scan using organ based tube current modulation[J]. Phys Med, 2018, 48: 72-75. DOI:10.1016/j.ejmp.2018.03.011 |
| [37] |
Yang Y, Zhuo W, Chen B, et al. A new phantom developed to test the ATCM performance of chest CT scanners[J]. J Radiol Prot, 2021, 41(2): 349. DOI:10.1088/1361-6498/abf900 |
| [38] |
Liu Q, Suleiman ME, McEntee MF, et al. Diagnostic reference levels in digital mammography: a systematic review[J]. J Radiol Prot, 2022, 42(1): 011503. DOI:10.1088/1361-6498/ac4214 |
| [39] |
王文静, 邱睿, 任丽, 等. 精细乳房模型及其在乳腺X射线摄影剂量评估中的应用[J]. 原子能科学技术, 2016, 50(11): 2085-2091. Wang WJ, Qiu R, Ren L, et al. Detailed breast model and its application to glandular dose estimation in mammography[J]. At Energy Sci Technol, 2016, 50(11): 2085-2091. DOI:10.7538/yzk.2016.50.11.2085 |
| [40] |
Wang W, Qiu R, Ren L, et al. Dose distribution in a breast undergoing mammography based on a 3d detailed breast model for chinese women[J]. Radiat Prot Dosimetry, 2018, 181(3): 221-228. DOI:10.1093/rpd/ncy017 |
| [41] |
Wang W, Qiu R, Ren L, et al. Monte Carlo calculation of conversion coefficients for dose estimation in mammography based on a 3D detailed breast model[J]. Med Phys, 2017, 44(6): 2503-2514. DOI:10.1002/mp.12210 |
| [42] |
Chang TY, Lai KJ, Tu CY, et al. Three-layer heterogeneous mammographic phantoms for Monte Carlo simulation of normalized glandular dose coefficients in mammography[J]. Sci Rep, 2020, 10(1): 2234. DOI:10.1038/s41598-020-59317-4 |
| [43] |
李孟阳, 王海云, 阮书州, 等. 蒙特卡罗方法评估冠状动脉介入术中患者器官剂量的转换系数[J]. 中华放射医学与防护杂志, 2022, 42(2): 137-143. Li MY, Wang HY, Ruan SZ, et al. Estimation on organ absorbed dose conversion coefficient for patients during coronary intervention procedure with Monte Carlo method[J]. Chin J Radiol Med Prot, 2022, 42(2): 137-143. DOI:10.3760/cma.j.cn112271-20210930-00399 |
| [44] |
王遥, 霍万里, 熊壮, 等. TACE手术中不同站姿下铅眼镜和铅面罩对医生眼晶状体防护效果的蒙特卡洛模拟比较[J]. 中国医学物理学杂志, 2016, 33(6): 553-558. Wang Y, Huo WL, Xiong Z, et al. Monte Carlo-based comparison of radiation protection efficiency of lead glasses vs. leadmask for eye lens of doctor in different standing postures during transcatheter arterial chemoembolization[J]. Chin J Med Phys, 2016, 33(6): 553-558. DOI:10.3969/j.issn.1005-202X.2016.06.003 |
| [45] |
Bhar M, Mora S, Kadri O, et al. Monte Carlo study of patient and medical staff radiation exposures during interventional cardiology[J]. Phys Med, 2021, 82: 200-210. DOI:10.1016/j.ejmp.2021.01.065 |
| [46] |
De Simoni M, Battistoni G, De Gregorio A, et al. A data-driven fragmentation model for carbon therapy gpu-accelerated Monte-Carlo dose recalculation[J]. Front Oncol, 2022, 12: 780784. DOI:10.3389/fonc.2022.780784 |
| [47] |
Zhou B, Yu CX, Chen DZ, et al. GPU-accelerated Monte Carlo convolution/superposition implementation for dose calculation[J]. Med Phys, 2010, 37(11): 5593-5603. DOI:10.1118/1.3490083 |
| [48] |
Bert J, Perez-Ponce H, El Bitar Z, et al. Geant4-based Monte Carlo simulations on GPU for medical applications[J]. Phys Med Biol, 2013, 58(16): 5593-5611. DOI:10.1088/0031-9155/58/16/5593 |
| [49] |
Maneval D, Ozell B, Després P. pGPUMCD: an efficient GPU-based Monte Carlo code for accurate proton dose calculations[J]. Phys Med Biol, 2019, 64(8): 085018. DOI:10.1088/1361-6560/ab0db5 |
| [50] |
Yang K, Li X, George Xu X, et al. Direct and fast measurement of CT beam filter profiles with simultaneous geometrical calibration[J]. Med Phys, 2017, 44(1): 57-70. DOI:10.1002/mp.12024 |
| [51] |
Whiting BR, Evans JD, Dohatcu AC, et al. Measurement of bow tie profiles in CT scanners using a real-time dosimeter[J]. Med Phys, 2014, 41(10): 101915. DOI:10.1118/1.4896196 |
| [52] |
Boone JM. Method for evaluating bow tie filter angle-dependent attenuation in CT: theory and simulation results[J]. Med Phys, 2010, 37(1): 40-48. DOI:10.1118/1.3264616 |
| [53] |
Kramer R, Cassola VF, Andrade MEA, et al. Mathematical modelling of scanner-specific bowtie filters for Monte Carlo CT dosimetry[J]. Phys Med Biol, 2017, 62(3): 781-809. DOI:10.1088/1361-6560/aa5343 |
| [54] |
陈鑫洁, 张敬娜, 张慧滔, 等. 基于CT扫描数据的X射线能谱估计方法[J]. 物理学报, 2023, 72(11): 118701-118711. Chen XJ, Zhang JN, Zhang HT, et al. X-ray energy spectrum estimation based on CT scan data[J]. Acta Phys Sin, 2023, 72(11): 118701-118711. DOI:10.7498/aps.72.20222307 |
| [55] |
Zhao W, Niu K, Schafer S, et al. An indirect transmission measurement-based spectrum estimation method for computed tomography[J]. Phys Med Biol, 2015, 60(1): 339-357. DOI:10.1088/0031-9155/60/1/339 |
| [56] |
Zhao W, Xing L, Zhang Q, et al. Segmentation-free X-ray energy spectrum estimation for computed tomography using dual-energy material decomposition[J]. J Med Imaging (Bellingham), 2017, 4(2): 023506. DOI:10.1117/1.JMI.4.2.023506 |
 2024, Vol. 44
2024, Vol. 44


