螺旋断层治疗系统,简称Tomo系统,治疗床前进的同时,机架360°旋转,并通过气动多叶准直器(multileaf collimator, MLC)的精确控制、调节每个投影内的束流强度,实现对复杂靶区的调强治疗[1]。尽管较高的剂量调制可以提高治疗的精确性,但同时也增加了治疗执行过程中的不确定性。因此,治疗前的剂量验证变得至关重要,以确保剂量计算的准确性和患者安全[2-3]。剂量验证通常使用二维或三维探测器阵列进行测量,通过比较实测剂量与计算剂量,评估γ通过率,从而判断治疗计划的可执行性[4]。虽然治疗计划的复杂性在一定程度上是必要的,但过高的复杂性可能会影响剂量计算和传递的准确性,进而影响剂量验证的通过率[5-6]。
Tomo系统治疗计划的复杂性主要与MLC打开时间的分布有关[7-9]。但关于Tomo治疗计划复杂性评估[10-11],及利用Tomo计划复杂性预测剂量验证通过率的研究相对较少,还处于起步阶段[12]。本研究旨在分析归一化计划复杂度评分(normalized plan complexity score, nPCS)与剂量验证通过率之间的线性相关性,探索使用nPCS评估Tomo治疗计划复杂性的可行性,进而为临床Tomo治疗计划的设计和优化提供参考,同时减少基于测量的剂量验证的需求。
资料与方法1. 临床资料:本研究回顾性分析了2020年1月至2022年11月在山西白求恩医院肿瘤放射治疗中心接受螺旋断层放射治疗的288例患者。其中,头颈部患者187例(头部130例,头颈部57例),腹盆部患者101例(腹部16例,盆腔85例)。所有患者的治疗计划均采用2.5 cm的射野宽度,螺距(pitch)值为0.287,初始调制因子(modulation factor, MF)根据计划难度在1.8至3.0之间选择。
2. 设备:治疗使用的设备为螺旋断层治疗系统Tomotherapy HD(美国安科锐公司),计划系统采用Tomo系统计划5.1.8.23版本。剂量验证使用的三维剂量验证设备为ArcCheck(Sun Nuclear,美国)。该设备为圆柱形,表面2.9 cm深度处分布有1 386个半导体探头,使用PMMA CavityPlugTM插件,配套分析软件为SNC 6.0。
3.剂量验证:在Tomo系统上,使用fine扫描模式(2 mm层厚)获取ArcCheck模体的MVCT图像用于建模。在DQA工作站,将患者的治疗计划移植至所建模体进行计算,计算得到的剂量分布通过DICOM导出到ArcCheck软件。由于ArcCheck单次有效测量距离为21 cm,为准确反映计划复杂性对剂量验证通过率的影响,本研究所选病例的靶区长度均 < 21 cm。
为减少Tomo系统机机械性能、剂量变化及人员摆位经验对剂量验证结果的影响,本研究在Tomo系统年检调试后,集中1个月内由固定物理师对所选病例的验证计划统一重新测量。验证设备ArcCheck探测器一致性和绝对剂量也在测量前重新校准。测量和计算的剂量分布比较采用的评估标准为:阈值水平10%,绝对剂量,全局、局部3%/2 mm、2%/2 mm、1%/1 mm的γ通过率。
4.计划复杂性参数:选取13个计划复杂性参数,其中2个治疗计划参数,11个反映叶片打开状态的参数。分别为:总治疗时间/处方(Total Time/Gy),实际调制因子(actual modulation factor, actual MF),投影时间(projection time, PT),投影时间与最大叶片打开时间的间隔Tgap,平均叶片打开时间(mean leaf open time, Mean LOT),打开时间分别 < 100、50、30 ms的叶片数占总叶片数的比例%LOT < 100 ms、%LOT < 50 ms、%LOT < 30 ms,打开时间比投影时间分别小20、5 ms的叶片数占总叶片数的比例%LOT < PT-20 ms、%LOT < PT-5 ms,叶片打开时间的变异性(leaf open time variability, LOTV),计划时间正弦图变化(plan time sinogram variation, PSTV),相邻叶片均关闭的开放叶片所占的比例(leaves with zero open neighbors score, L0NS)[10]和由最右侧和最左侧打开的叶片定义的治疗范围内,关闭的叶片数占总叶片数的比例(closed leaf score, CLSin)[10]。
5.主成分分析法和复杂性评分:主成分分析法是一种多元统计技术,通过寻找一组新的不相关变量——主成分(principal component, PC),来降低大数据集的维度。本研究设定总方差累积百分比的预定义截止点为60%~80%。
计划复杂性评分(plan complexity score, PCS):保留主成分的加权平均值,即:
| $ \operatorname{PCS}=\sum\limits_{k=1}^n \frac{v_k}{v} \times P C_k $ | (1) |
式中,n为所保留主成分个数,v为由保留的主成分解释的总方差,vk为由PCk解释的方差百分比。
但PCS可以有正值和负值,而它的绝对值又可能很难解释。因此对给定的计划i计算计划复杂性评分的标准化版本nPCS,即:
| $ \mathrm{nPCS}_i=\frac{P C S_i-\min P C S}{\max P C S-\min P C S} $ | (2) |
nPCSi在0和1之间变化。nPCSi值越高,计划复杂性越大。
6. 统计学处理:采用SAS 9.4软件进行统计分析。计量资料数据符合正态分布以x±s来表示,采用独立样本t检验对头颈部、腹盆部计划的13个复杂性参数进行统计学分析。P < 0.05为差异有统计学意义。
通过计算斯皮尔曼相关系数rs分析复杂性参数之间的相关性。根据rs的绝对值,相关性的强度被分为:0~0.19“非常弱”、0.20~0.39“弱”、0.40~0.59“中等”、0.60~0.79“强”和0.80~1“非常强”。
利用多重线性回归评估提取的各主成分、nPCS与不同标准验证通过率的相关性,并采用独立样本t检验比较不同治疗部位治疗计划的nPCS的差异。由于3%/2 mm(全局)为临床分析验证通过率时最常采用的标准,本研究只选用与3%/2 mm(全局)验证通过率关联有显著性的主成分计算叶片复杂性评分nPCS。
结果1. 参数比较:表 1比较了头颈部、腹盆部两组的计划复杂性参数,其中参数LOTV、PSTV、CLSin、actual MF和Total Time/Gy的差异有统计学意义(t=-5.15、3.20、4.12、3.00、-4.85,P < 0.05)。
|
|
表 1 头颈部、腹盆部计划复杂性参数的比较(x±s) Table 1 Comparison of complexity parameters between head and neck plans and abdominal-pelvic plans (x±s) |
表 2比较了头颈部、腹盆部两组的γ通过率,标准为2%/2 mm(局部)、1%/1 mm(全局)、1%/1 mm(局部)时两组的γ通过率差异有统计学意义(t=2.89、-2.46、3.83,P < 0.05)。
|
|
表 2 头颈部、腹盆部计划γ通过率的比较(%,x±s) Table 2 Comparison of gamma pass rates between head and neck plans and abdominal-pelvic plans (%, x±s) |
2. 计划复杂性参数相关性分析:13个复杂性参数之间具有非常强正相关性的是:%LOT < 30 ms与%LOT < 50 ms(rs=0.97,P < 0.001),%LOT < PT-5 ms与%LOT < PT-20 ms(rs=0.98,P < 0.001),PSTV与Mean LOT(rs=0.91,P < 0.001)。具有强正相关性的是:%LOT < 50 ms与%LOT < 100 ms(rs=0.74,P < 0.001),%LOT < 30 ms与%LOT < 100 ms(rs=0.64,P < 0.001),PSTV与%LOT < PT-5 ms(rs=0.60,P < 0.001),L0NS与%LOT < PT-5 ms(rs=0.60,P < 0.001);具有强负相关的是:%LOT < 100 ms与Mean LOT(rs=-0.67,P < 0.001),详见图 1。

|
注:Tgap. 投影时间与最大叶片打开时间的间隔;Mean LOT. 平均叶片打开时间;%LOT < 100 ms、%LOT < 50 ms、%LOT < 30 ms. 打开时间分别 < 100、50、30 ms的叶片数占总叶片数的比例;%LOT < PT-20 ms、%LOT < PT-5 ms. 打开时间比投影时间分别小20、5 ms的叶片数占总叶片数的比例;LOTV. 叶片打开时间的变异性;PSTV. 计划时间正弦图变化;L0NS. 相邻叶片均关闭的开放叶片所占的比例;CLSin. 由最右侧和最左侧打开的叶片定义的治疗范围内关闭的叶片数占总叶片数的比例;actual MF. 实际调制因子;Total Time/Gy.总治疗时间/处方 图 1 计划复杂性参数的斯皮尔曼相关系数(rs)的热力图 Figure 1 Heat map showing the Spearman correlation coefficients (rs) of the plan complexity parameters |
3.计划复杂性参数的主成分分析:根据总方差的累积百分比的预定义截止点60%~80%,需选取4个主成分。这4个主成分PC1、PC2、PC3、PC4分别解释总方差的33.5%、24.4%、11.4%、9.2%,共解释总方差的78.48%。
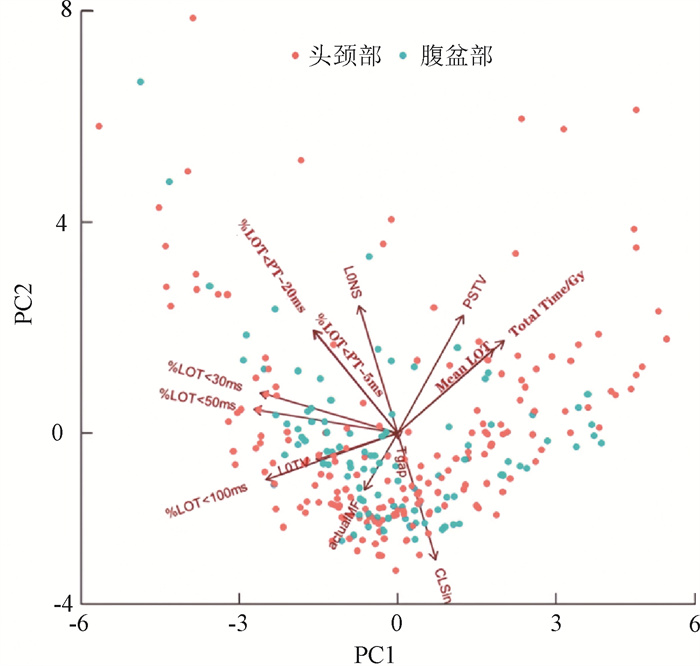
从主成分PC1、PC2的双标图可见,复杂性参数Mean LOT与Total Time/Gy,%LOT < PT-20 ms与%LOT < PT-5 ms,%LOT < 100 ms与LOTV的正相关特别强;L0NS与CLSin,PSTV与actual MF,Mean LOT与%LOT < 100 ms的负相关特别强。另外,描述头颈和腹盆两个部位的计划复杂度参数没有特异性(图 2)。
|
注:横坐标为复杂性参数的主成分PC1的权重,纵坐标为其主成分PC2的权重。若两个变量有较大的正相关,则对应的向量很接近;如果较弱,它们之间的夹角在90°左右,当负且强时,夹角接近180°。图中每个点为计划数据集中的一个计划,红色点为头颈部计划,蓝色点为腹盆部计划 图 2 计划复杂性参数的主成分PC1、PC2的双标图 Figure 2 Biplot of principal components PC1 and PC2 of the plan complexity parameters |
4. 多重线性回归分析:主成分PC1、PC2和PC3分别与3%/2 mm(全局)标准的γ通过率线性相关(β=0.34, ,0.31,0.62,P < 0.05);标准化复杂性评分nPCS与3%/2 mm(全局)、1%/1 mm(全局)标准的γ通过率线性相关(β=5.36,32.51,P < 0.001),详见表 3。
|
|
表 3 主成分、计划复杂性评分与不同标准γ通过率的相关性 Table 3 Correlations of principal components and plan complexity score with gamma pass rates based on different criteria |
5.不同部位计划复杂性评分比较:头颈部和腹盆部计划的标准化复杂性评分nPCS的分布基本相似,差异无统计学意义(P>0.05)。但最复杂的计划属于头颈部,nPCS=1。
讨论Tomo系统的治疗计划存在多个自由度,且不能完全被治疗计划系统报告的参数所描述。Bresciani等[13]研究Tomo系统的384个治疗计划发现,治疗参数如治疗床运动距离、床速、机架旋转圈数、机架周期等与剂量验证通过率之间没有相关性。因此,本研究未将这些参数纳入考量。Tomo系统通过调整MLC叶片在不同投影中的打开时间来调制束流强度,即使是微小的误差也可能导致剂量的偏差。在治疗计划优化阶段,物理师设定的Pitch和MF参数,实际上调整的是叶片打开时间的复杂性,这比传统的治疗参数更能直接反映治疗过程中叶片运动的复杂度[14]。
本研究选取的13个复杂性参数,从治疗时长[15]、叶片关闭时间不足[9]、治疗时长短的子野占比[7, 16]、调制度[17-18]、凹凸槽效应[19]等多个方面研究Tomo系统治疗计划的复杂性。常规直线加速器的治疗计划中,总治疗跳数(Total MU)是最简单、使用最广泛的复杂性指标[15]。Tomo系统的Total Time与直线加速器的Total MU一样,均反映子野的复杂程度。Total Time/Gy虽排除了处方剂量对治疗时间的影响,但在一定程度还依赖靶区长度和计划的pitch值。Tgap、%LOT < PT-20 ms、%LOT < PT-5 ms用于反映叶片关闭不足引入的误差。%LOT < PT-20 ms、%LOT < PT-5 ms的值越大,来不及关闭的叶片数可能越多,引入的误差可能越大。Tgap则反映最大时间附近的叶片由于来不及关闭直接进入下一个投影而带入的时间误差,对实际照射剂量的影响[9]。Mean LOT、%LOT < 100 ms、%LOT < 50 ms、%LOT < 30 ms均反映治疗时间短的子野所占的比例,值越大,越容易导致剂量误差[7, 16]。LOTV、MF和PSTV则反映了调制度,PSTV的值越大、LOTV的值越小均表示叶片打开时间的变化越大;MF值越大则表示叶片最大打开时间与平均打开时间的比值越大。L0NS反映了叶片的凹凸槽效应,值越大,凹凸槽效应越明显。CLSin反映了治疗范围内每个控制点闭合叶片数的比例,值越高可认为计划越复杂[10]。
复杂性参数之间相互影响,13对复杂性参数,非常强相关的3对,强相关的有5对,%LOT < 100 ms与Mean LOT则表现为负的强相关。故本研究采用主成分分析法提取新的不相关变量,避免参数之间强相关性对研究结果的影响。文中使用方差解释性最强的2个主成分做双标图,并未发现数据点有分簇现象,说明本数据组描述头颈和腹盆两个部位治疗计划的复杂性参数没有特异性,这与Santos等[10]的研究结果不同。Santos等[10]的数据组中,描述头颈部计划占比最高的复杂性参数是%LOT < 100 ms,%LOT < 50 ms,%LOT < 30 ms,MI, PSTV和CLSin;描述头部立体定向计划占比最高的是Mean LOT、CLS、L1NS和LOTV;描述前列腺计划的介于头颈部与头部立体定向两组计划之间。两个研究结果不同的原因可能是,Santos等[10]数据组每部位基本是单一病种,而本研究每个部位都有不同的病种,但准确原因仍需更多地研究进行确认。
本研究复杂性评分nPCS与3%/2 mm(全局)、1%/1 mm(全局)标准的γ验证通过率呈显著线性相关,Santos等[10]的研究中,nPCS与2%/2 mm(全局)标准的γ验证通过率也呈现中等相关性。故使用nPCS评价计划可执行性具有可行性。另使用nPCS比较不同部位治疗计划的复杂性时,Santos等[10]的研究数据组中头颈部计划最复杂的,其次是前列腺和脑立体定向治疗计划。而本文数据组头颈部和腹盆计划具有相近的复杂度,差别无统计学意义。可见单纯依据部位判断计划的复杂度并不客观,而复杂度评分的引入正好解决这个问题。值得注意的是,计划复杂度评分nPCS只能比较同一数据组内各治疗计划的相对复杂程度,不同数据组的nPCS数值比较没有意义。
对于全脑全脊髓和部分宫颈>21 cm的超长靶区,若采用常规等中心摆位的剂量验证方法,可能直接照射到ArcCheck的电子元件部分造成设备损坏。目前,常见有两种方法解决ArcCheck有效测量长度不足的问题。一种是移动摆位中心进行测量[20],但可能造成测量范围不全;一种是使用ArcCheck的merge功能分段测量后进行拼接模拟完整靶区的测量[21]。但使用这两种方法,对治疗计划验证通过率的影响如何,目前尚无相关研究。所以本研究只选取靶区范围 < 21 cm的病例,超长靶区计划复杂性和验证通过率的关系将在今后的研究中专门讨论。
本研究的不足,所选复杂性参数主要反映叶片打开时间的复杂程度,并且数目比较少也不尽全面。后期将尝试选用更多的复杂性参数,且结合临床和剂量组学的特征,更全面地反映治疗计划的复杂性。同时,使用人工智能的方法预测剂量验证通过率也是未来工作的方向。
综上所述,基于主成分分析的nPCS能有效评估治疗计划的可执行性,并比较不同治疗计划的复杂性。这将有助于为临床Tomo治疗计划的设计和减少基于测量的剂量验证提供参考依据。
利益冲突 本研究由署名作者按以下贡献声明独立开展,排名无争议,文章不涉及任何利益冲突
作者贡献声明 金晓丽负责课题研究组织实施及论文撰写;王雪娜负责研究方案的修改和实验数据的统计学分析;郭睿、侯旭、兰越、赵晓杰负责剂量验证数据的采集
| [1] |
Mackie TR, Holmes T, Swerdloff S, et al. Tomotherapy: a new concept for the delivery of dynamic conformal radiotherapy[J]. Med Phys, 1993, 20(6): 1709-1719. DOI:10.1118/1.596958 |
| [2] |
Fenwick JD, Tomé WA, Jaradat HA, et al. Quality assurance of a helical tomotherapy machine[J]. Phys Med Biol, 2004, 49(13): 2933-2953. DOI:10.1088/0031-9155/49/13/012 |
| [3] |
Thomas SD, Mackenzie M, Field GC, et al. Patient specific treatment verifications for helical tomotherapy treatment plans[J]. Med Phys, 2005, 32(12): 3793-3800. DOI:10.1118/1.2134929 |
| [4] |
Low DA, Harms WB, Mutic S, et al. A technique for the quantitative evaluation of dose distributions[J]. Med Phys, 1998, 25(5): 656-661. DOI:10.1118/1.598248 |
| [5] |
Park JM, Choi CH, Wu HG, et al. Correlation of the gamma passing rates with the differences in the dose-volumetric parameters between the original VMAT plans and actual deliveries of the VMAT plans[J]. PLoS One, 2020, 15(12): e0244690. DOI:10.1371/journal.pone.0244690 |
| [6] |
Shen Z, Tan X, Li S, et al. Correlation between the γ passing rates of IMRT plans and the volumes of air cavities and bony structures in head and neck cancer[J]. Radiat Oncol, 2021, 16(1): 134. DOI:10.1186/s13014-021-01861-y |
| [7] |
Westerly DC, Soisson E, Chen Q, et al. Treatment planning to improve delivery accuracy and patient throughput in helical tomotherapy[J]. Int J Radiat Oncol Biol Phys, 2009, 74(4): 1290-1297. DOI:10.1016/j.ijrobp.2009.02.004 |
| [8] |
Templeton AK, Chu JC, Turian JV. The sensitivity of ArcCHECK-based gamma analysis to manufactured errors in helical tomotherapy radiation delivery[J]. J Appl Clin Med Phys, 2015, 16(1): 4814. DOI:10.1120/jacmp.v16i1.4814 |
| [9] |
岳麒, 段继梅, 王志伟, 等. 螺旋断层治疗计划系统升级前后验证结果及叶片打开时间对比研究[J]. 中华放射肿瘤学杂志, 2021, 30(4): 382-386. Yue L, Duan JM, Wang ZW, et al. Comparison of validation results and leaf open time before and after upgrading of helix tomotherapy planning system[J]. Chin J Radiat Oncol, 2021, 30(4): 382-386. DOI:10.3760/cma.j.cn113030-20190726-00290 |
| [10] |
Santos T, Ventura T, Mateus J, et al. On the complexity of helical tomotherapy treatment plans[J]. J Appl Clin Med Phys, 2020, 21(7): 107-118. DOI:10.1002/acm2.12895 |
| [11] |
Cavinato S, Fusella M, Paiusco M, et al. Quantitative assessment of helical tomotherapy plans complexity[J]. J Appl Clin Med Phys, 2023, 24(1): e13781. DOI:10.1002/acm2.13781 |
| [12] |
Cavinato S, Bettinelli A, Dusi F, et al. Prediction models as decision-support tools for virtual patient-specific quality assurance of helical tomotherapy plans[J]. Phys Imaging Radiat Oncol, 2023, 26: 100435. DOI:10.1016/j.phro.2023.100435 |
| [13] |
Bresciani S, Miranti A, Di Dia A, et al. A pre-treatment quality assurance survey on 384 patients treated with helical intensity-modulated radiotherapy[J]. Radiother Oncol, 2016, 118(3): 574-576. DOI:10.1016/j.radonc.2015.12.021 |
| [14] |
Binny D, Lancaster CM, Harris S, et al. Effects of changing modulation and pitch parameters on tomotherapy delivery quality assurance plans[J]. J Appl Clin Med Phys, 2015, 16(5): 87-105. DOI:10.1120/jacmp.v16i5.5282 |
| [15] |
Crowe SB, Kairn T, Kenny J, et al. Treatment plan complexity metrics for predicting IMRT pre-treatment quality assurance results[J]. Australas Phys Eng Sci Med, 2014, 37(3): 475-482. DOI:10.1007/s13246-014-0274-9 |
| [16] |
Chen Q, Westerly D, Fang Z, et al. TomoTherapy MLC verification using exit detector data[J]. Med Phys, 2012, 39(1): 143-151. DOI:10.1118/1.3666762 |
| [17] |
Coselmon MM, Moran JM, Radawski JD, et al. Improving IMRT delivery efficiency using intensity limits during inverse planning[J]. Med Phys, 2005, 32(5): 1234-1245. DOI:10.1118/1.1895545 |
| [18] |
McNiven AL, Sharpe MB, Purdie TG. A new metric for assessing IMRT modulation complexity and plan deliverability[J]. Med Phys, 2010, 37(2): 505-515. DOI:10.1118/1.3276775 |
| [19] |
Sevillano D, Minguez C, Sanchez A, et al. Measurement and correction of leaf open times in helical tomotherapy[J]. Med Phys, 2012, 39(11): 6972-6980. DOI:10.1118/1.4762565 |
| [20] |
周本梅, 查小英, 谭拥, 等. 运用ArcCHECK实施宫颈癌超长靶区的剂量验证[J]. 中华放射医学与防护杂志, 2023, 43(8): 601-606. Zhou BM, Zha XY, Tan Y, et al. Applying an ArcCHECK detector to the dose verification for ultra-long target volumes of cervical cancer[J]. Chin J Radiol Med Prot, 2023, 43(8): 601-606. DOI:10.3760/cma.j.cn112271-20230208-00029 |
| [21] |
解传滨, 徐寿平, 徐伟, 等. 运用ArcCHECK实施旋转调强全脊髓照射超长靶区的计划验证[J]. 中国医疗器械杂志, 2015, 39(1): 68-71. Xie CB, Xu SP, Xu W, et al. Patient-specific dose verification method using ArcCHECK for total marrow irradiation with intensity modulated arc therapy[J]. Chin J Med Instrum, 2015, 39(1): 68-71. DOI:10.3969/j.issn.1671-7104.2015.01.019 |
 2024, Vol. 44
2024, Vol. 44
