2. 中山大学肿瘤防治中心放疗科, 华南肿瘤学国家重点实验室, 肿瘤医学协同创新中心, 广州 510060
2. Collaborative Innovation Center for Cancer Medicine, State Key Laboratory of Oncology in South China, Department of Radiation Oncology, Sun Yat-sen University Cancer Center, Guangzhou 510060, China
碳离子放射治疗(CIRT)因辐射质具有高传能线密度(LET)和独特的布拉格峰剂量学特性,能有效精准照射肿瘤组织,同时显著减少对周围正常组织的辐射剂量,成为近年来放疗技术发展的重点之一[1]。相对生物效能(RBE)可以刻画碳离子与常规光子束产生相同生物效应时的剂量差异,是碳离子放疗这一新兴技术得以安全临床实施的重要剂量依赖量[2]。然而,通过细胞实验获取的碳离子RBE值仅适用于特定的粒子类型、能量和生物终点。为了经济有效地计算临床场景下的碳离子的RBE值,有学者提出了以LQ模型[3-4]为代表的现象学模型和目前广泛应用于临床考虑微米尺度上能量沉积分布的局部效应模型(LEM)[5-6]、微剂量动力学模型(MKM)[7-8]。但越来越多的研究表明,细胞的初始辐射损伤与DNA尺度上带电粒子产生的电离团簇大小密切相关,因此纳剂量学量被视为描述粒子径迹结构和揭示碳离子RBE本质特征的更优量度[9],从而发展出了基于DNA损伤修复的纳剂量学模型。然而这些纳剂量学模型忽略了碳离子与物质发生相互作用过程中次级粒子造成的生物效应[10-12],这些次级粒子具有不同生物效应且在布拉格峰后沉积不可忽略的剂量,导致布拉格峰后生物剂量评估不准确,可能引起关键器官的放射毒性和继发性诱发肿瘤[13]。
为解决现有模型缺陷,本研究结合宏观和微观两种尺度的蒙特卡罗(蒙卡)模拟,采用两种经过广泛验证的蒙卡模拟软件进行实验仿真[14-15],基于纳剂量学DNA损伤和细胞DNA损伤修复机制,构建细胞生存率预测模型,并提出剂量加权方法,以精准表征混合束诱导的DNA损伤特性,综合考虑了初级与次级粒子的生物学效应,从而提高了细胞生存率的预测准确度。
材料与方法1. 模拟设置
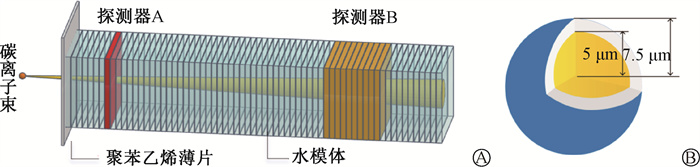
(1) 宏观尺度碳离子束模拟设置:研究使用TOPAS(TOol for PArticle Simulation)3.8版本进行宏观尺度蒙卡模拟[14],仿真Buglewicz等[13]采用HIMAC产生290 MeV/u碳离子射束照射细胞培养瓶的离体细胞实验。图 1所示为仿真实验过程中的模体设置,在水模体前放置2 mm厚的聚苯乙烯薄片模拟细胞培养瓶底厚度。水模体尺寸设置为0.4 cm×0.4 cm×20 cm的长方体,物理过程设置为QG_SP_BIC_HP。270.5 MeV/u的单能碳离子束从模体左侧面中心位置垂直入射,在竖直和水平方向上呈现高斯分布δx=δy=1 mm(半峰全宽为2.35 mm),散射角度设置为None(如图 1所示)。入射碳离子数目根据探测器A(10 mm处)的测量结果决定,当探测器A处沉积剂量为分别2、3、5和10 Gy时停止入射。并在布拉格峰及峰后(140~180 mm)放置探测器B逐毫米统计模体内碳离子及其次级粒子的通量、剂量和能谱分布。
|
图 1 TOPAS模拟设置(A)与MCDS细胞设置示意图(B) Figure 1 Schematic diagrams showing the TOPAS simulation setting (A) and MCDS cell setting (B) |
(2) 微观尺度DNA损伤模拟设置:使用蒙特卡罗损伤模拟(MCDS)2.01版本计算细胞在不同辐射质条件下的DNA损伤数据[15],基于CIRT中碳离子及其主要次级粒子类型和能量[16]预先构建0.1~1 000 MeV的H+离子和1~1 000 MeV/u的He2+、Li3+、Be4+、B5+、C6+、N7+、O8+离子的DSB损伤数据查找表。CHO细胞模型如图 1所示,细胞核半径为5 μm,细胞核内DNA数量为5.6 Gbp[5]。由于高LET粒子束氧效应不明显,富氧与乏氧细胞表现出类似的放射敏感性,乏氧细胞也可以产生严重的辐射损伤,因此设置氧含量浓度为100%,即760 mmHg[18-19]。为确保模拟结果不确定度低于1%,模拟粒子数设置为106个。同时,本研究也将不同水下深度处获取的碳离子及其次级粒子能谱分布作为输入,直接获得不同深度处混合束的DSB损伤参数。
2. 混合束辐射致细胞损伤修复模型构建与参数拟合
(1) 混合束DNA损伤表征:对于在给定宏观体积(例如毫米大小的体素)中发生相互作用的辐射场,该体积中的平均DNA损伤数量可以通过辐射场中与粒子径迹相关的每个粒子的DNA损伤数加权得到。由于预先计算的单能粒子DNA损伤数量以剂量归一化,因此,本研究选择剂量作为对宏观体素中混合束辐射特征的加权量,混合束DNA损伤表征公式如下:
| $ \bar{\lambda}_p=\frac{\sum\limits_{p, E}\left(\lambda_p\right)_{p, E} \Delta D_{p, E}}{\sum\limits_{p, E} \Delta D_{P, E}} $ | (1) |
| $ \bar{Y}=\frac{\sum\limits_{p, E} Y_{p, E} \Delta D_{p, E}}{\sum\limits_{p, E} \Delta D_{p, E}} $ | (2) |
式中,(λp)p, E为每个能量为E类型为p造成DSB损伤的初级粒子产生DSB的平均数量,Gy-1/细胞;Yp, E为能量为E的p类型粒子在一个细胞沉积1 Gy剂量的DSB数量,Gy-1/细胞;ΔDp, E为宏观体素内能量为E的p类型粒子沉积的剂量,Gy;Ȳ为混合束在每个细胞沉积1 Gy剂量的DSB平均数量;
(2) 辐射致细胞损伤修复模型构建与参数拟合:本研究基于先前已有的辐射致DNA损伤修复模型[12],将细胞存活率与剂量和DSB损伤数量联系起来,如公式(3)~(5)所示:
| $ \alpha=Y \times\left(\frac{1-e^{-\zeta \lambda_p}}{\zeta \lambda_p}\right) \times\left(1-\mu_x\left(\frac{1-e^{-\xi \lambda_p}}{\xi \lambda_p}\right)\right) \times \mu_y $ | (3) |
| $ \beta=\frac{1}{2} \eta\left(\lambda_p\right) \frac{Y}{\lambda_p} \times Y \times\left(\frac{1-e^{-\zeta \lambda_p}}{\zeta \lambda_p}\right) \times\left(\frac{1-e^{-\xi \lambda_p}}{\xi \lambda_p}\right) \times \mu_x \mu_y $ | (4) |
| $ -\ln S=\alpha D+\beta D^2 $ | (5) |
式中,Y为由MCDS计算得到的每细胞沉积1 Gy剂量的DSB平均数量;λp为由MCDS计算得到的引起DSB的每个初级粒子产生的DSB的平均数量;D为剂量;α和β分别为直接和间接致死系数;S为细胞存活率;μx、μy、ζ、ξ和η(λp)为根据离体细胞实验得到的拟合值。本研究基于PIDE数据库[17]扩充了先前模型仅基于Furusawa等[20]的52条离体细胞实验数据,为解决PIDE数据集中的离群数据和缺失数据对模型的影响,研究筛选掉数据库中α < 0.03 Gy-1和β < 0.001 Gy-2的数据,最终考虑的CHO实验数据包含H+、He2+、C6+、Ne10+ 4种射束,LET范围为1~700 keV/μm,共131条。通过最小二乘法拟合出一组适用于各种主要次级粒子类型的最优参数。
3. 模型准确性验证:考虑到实际治疗计划中单次剂量值,本研究仅通过对比探测器A位置处沉积2 Gy剂量时,探测器B不同位置深度MCDS模拟混合束
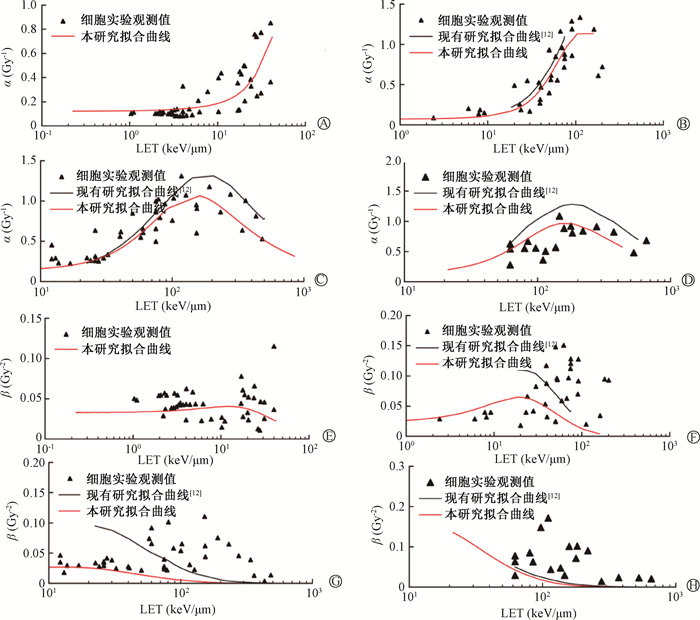
1. 模型关键参数α、β值的精确性:本研究采用最小二乘法进行参数拟合。经拟合后,中间参数μx、μy、ζ、ξ、ηλp→1和ηλp→∞分别取值为0.932 5、0.031 2、0.054 5、0.060 5、0.001 6、0.003 1。在此基础上进一步计算的He2+、C6+、Ne10+粒子类型射束关键参数α与离体细胞实验数值误差(RMSE)分别为0.203 9、0.192 0、0.516 9 Gy-1,相较于现有研究所报道[12]的0.211 8、0.235 6、0.382 5 Gy-1,整体提升7.68%。另一模型关键参数β值拟合误差则为0.059 8、0.040 5、0.060 5 Gy-2,较现有研究[12]所报道的0.060 3、0.046 2、0.058 6 Gy-2,整体提升0.65%。其中,Ne10+粒子类型射束的关键参数拟合误差有较小幅度的上升,其原因是实验纳入现有研究未经报道的H+粒子类型射束的关键模型参数α和β进行拟合。H+粒子类型α和β值拟合误差分别为0.139 2 Gy-1和0.020 5 Gy-2。具体拟合情况见图 2。
|
A、B、C、D. 分别为H+、He2+、C6+、Ne10+射束的α值;D、E、F、G. 分别为H+、He2+、C6+、Ne10+射束的β值 图 2 本研究与现有研究[12]对模型关键参数α、β的拟合效果比较 A, B, C, D. The α values for H+, He2+, C6+, Ne10+ beams; E, F, G, H. The β values for H+, He2+, C6+, Ne10+ beams Figure 2 Comparison of observed and predicted values for α and β in the pide dataset |
2. 宏观及微观蒙卡模拟结果
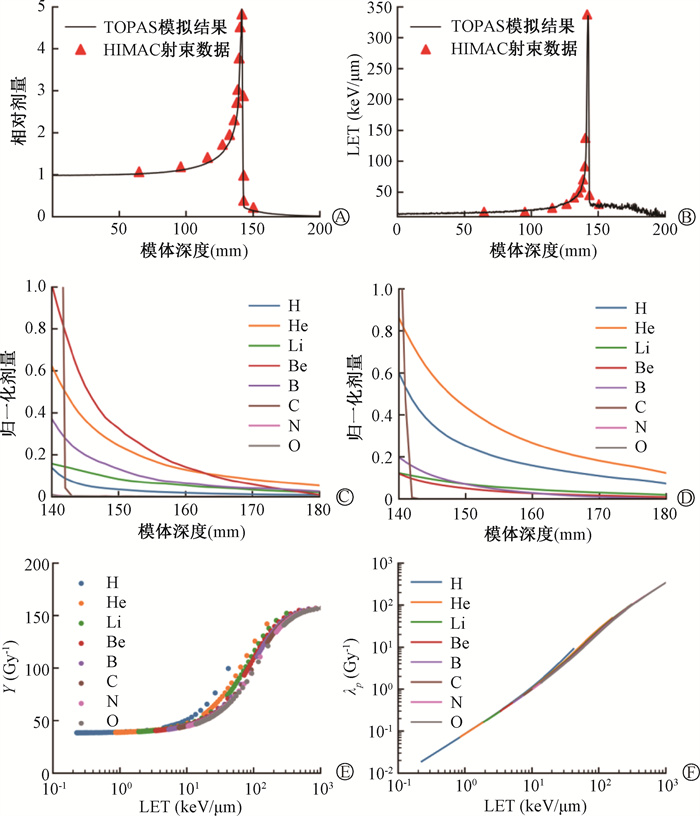
(1) 模拟射束与实验射束一致性评估:Buglewicz等[13]公布射束信息显示,射束入射位置处LETd值为13.4 keV/μm,在142 mm深度处达到LETd峰值337 keV/μm。布拉格峰位于141.4 mm处,峰值剂量与射束入射点剂量比为4.8。布拉格峰后148.8 mm处剂量与射束入射点剂量比为0.35。如图 3所示,本研究模拟的碳离子射束深度剂量分布与离体细胞实验射束吻合。
|
A. 深度剂量分布;B. LET深度分布;C.布拉格峰后不同粒子归一化深度剂量分布;D. 布拉格峰后不同粒子归一化深度通量分布;E. 不同粒子类型不同LET值的Y值;F. 不同粒子类型不同LET值的λp值 图 3 碳离子束辐射特性及其主要次级粒子DNA损伤特性 A. Depth-dose distribution; B. Depth distribution of LET; C. Normalized depth-dose distributions of different particles beyond the Bragg peak; D. Normalized depth-flux distributions of different particles beyond the Bragg peak; E. Y-values of different particle types and LET values; F. λp-values for different particle types and LET values Figure 3 Radiation characteristics of carbon ion beams and DNA damage characteristics of their major secondary particles |
(2) 布拉格峰及峰后粒子谱分布:由于碳离子相对原子序数较大,与模体发生相互作用产生较多的次级粒子且在布拉格峰后起到主要影响作用,因此实验逐毫米统计140~180 mm范围内的粒子能谱分布,图 3为按140 mm处粒子最大通量和剂量进行归一化的结果
(3) 碳离子及主要次级粒子DNA损伤数据库:根据碳离子放疗初级及次级粒子能量范围,本实验以10 MeV/u的能量间隔构建了碳离子及其主要次级粒子的DNA损伤数据如图 3所示。
3. 剂量加权方式表征混合束DNA损伤特性准确性:在探测器A位置处沉积2 Gy剂量时,探测器B不同位置深度处MCDS模拟的混合束Ȳ、

|
A. 混合束在不同深度处Ȳ值;B. 混合束在不同深度处 |
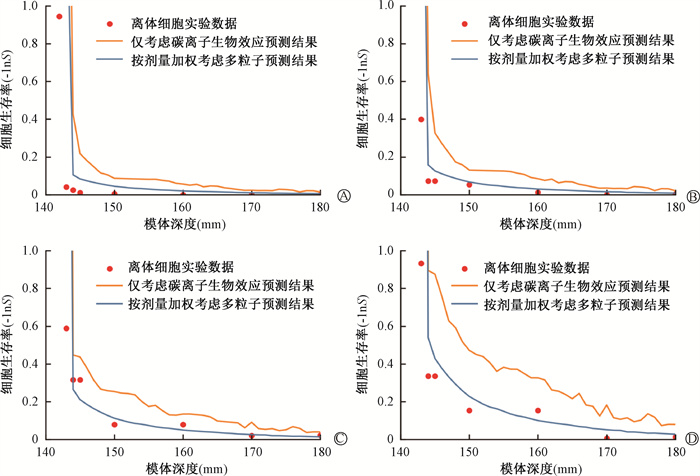
4. 模型预测混合束细胞生存率准确性:图 5显示了290 MeV/u单能碳离子射束入射模体,当探测器A位置处沉积剂量分别为2、3、5和10 Gy时,Buglewicz等[13]布拉格峰及峰后(140~180 mm)的离体细胞生存率实验值与仅考虑碳离子生物效应和剂量加权方式表征辐射束DSB损伤能力的模型预测值之间的差异。其中仅考虑碳离子生物效应表征混合束DSB损伤能力的方式,依据射束LETd值将所有次级粒子的生物效应等同于碳离子。4种不同剂量条件下,仅考虑碳离子和采用按照剂量加权方式预测的结果在布拉格峰区(140~142 mm)范围内与离体细胞实验测量值的误差均值与方差分别为0.6%±0.4%和0.3%±0.24%,在布拉格峰后(142~180 mm)与离体细胞实验测量值的误差均值与方差分别为4.6%±0.4%和2.3%±0.24%。
|
A、B、C、D. 分别对应探测器A沉积2、3、5和10 Gy条件下布拉格峰及峰后细胞生存率 图 5 采用不同方式表征混合束生物效应的细胞生存率预测值比较 A, B, C, and D. Correspond to cell survival rates at and beyond the Bragg peak for detector A under deposition of 2, 3, 5, and 10 Gy, respectively Figure 5 Comparison of predicted cell survival rates under the characterization of the biological effects of mixed beam using different methods |
讨论
碳离子放疗中产生的次级粒子在布拉格峰后产生了不可忽略的剂量[21-22],且不同次级粒子类型具有不同的生物效应,因此,准确描述碳离子混合束的微观辐射特性能够提高布拉格峰后生物损伤预测的准确性。本研究基于宏观和微观蒙卡模拟建立细胞生存预测模型,根据获取的碳离子布拉格峰及其峰后粒子谱分布,并通过剂量加权方式表征混合束致细胞损伤特性,预测的布拉格峰后细胞生存曲线与实验结果吻合良好。相比于仅考虑碳离子的细胞生存预测结果,本研究方法显著提升了布拉格峰后细胞生存预测准确性。
本研究所提出的基于微观和宏观蒙卡模拟框架并采用剂量加权表征混合束诱导DNA损伤的方式能准确预测细胞存活率。本研究模拟获取的布拉格峰后粒子谱分布中,碳离子含量直线下降,主要剂量来自氦、铍、硼等核碎片,这与Buglewicz等[13]的离体细胞实验结论一致。不同粒子DNA损伤数据表明,当LET值为10~200 keV/μm之间时,不同类型粒子导致DSB平均数差距较大,当LET>200 keV/μm时,不同粒子间造成的DSB损伤数量差距缩小,该趋势与现有研究结论一致[3-8, 23],这是由于粒子径迹随LET增大而收缩产生超杀效应导致的。而布拉格峰前后大多数粒子LET值落在10~200 keV/μm区间内,因此在布拉格峰后区别考虑不同粒子类型造成的DNA损伤能更准确描述混合束的微观辐射特性。本研究通过纳入更多的离体细胞实验数据拟合模型的新参数,使得H+、He2+、C6+离子的模型预测值与实验观测值间总体一致性得到改善,尤其对于α值的预测准确性提升明显,并可以将其扩展到更广的LET区域,解决目前主流细胞生存率预测模型在高LET能量范围无法描述超杀效应的问题[5-8]。实验新纳入碳离子治疗中主要的次级粒子类型H+数据,导致模型预测结果与Ne10+实验数据一致性较现有研究[12]略有下降,但鉴于Ne10+不是碳离子治疗的主要次级粒子,因此不会降低模型预测碳离子治疗混合束细胞生存率的精度。
然而,模型对实验数据中离散程度较高的β值预测准确性略有欠缺。目前已有研究指出β项可能与细胞的修复机制密切相关[10-12]。而本研究所构建的模型主要聚焦于双链断裂(DSB)及非同源末端连接(NHEJ)修复对细胞生存率的影响,这一局限可能导致对处于S期末期和G2期的细胞生存率预测存在低估现象[24]。此外,Henthorn等[25]和Nickoloff等[26]的研究成果进一步揭示了DNA损伤复杂性与辐射束线性能量转移(LET)之间的联系,这种复杂性变化进而影响细胞生存率。鉴于此,在后续研究中将针对不同DNA损伤类型及其相应的修复通路进行更为详尽的考量与整合,以全面提升模型的预测精度。目前,碳离子放疗计划中常用RBE定量描述其相对于光子束造成生物效应,由于肿瘤和正常组织的临床效应终点和辐射敏感性不同,因此以细胞生存率为生物终点的生物RBE值需要转化为临床RBE才能用于计划评估[27-28]。为了将本研究模型用于评估临床碳离子计划的RBE和生物剂量,后续将进一步研究次级粒子对临床碳离子计划的影响,并基于在体实验数据和临床结果分析进一步验证和完善该模型。
利益冲突 所有作者均声明不存在利益冲突
作者贡献声明 林洁负责设计研究方案,实验数据及文献查找、研究实施及论文撰写;李永宝、周凌宏、宋婷负责提出研究思路,技术指导及论文修改
| [1] |
Tinganelli W, Durante M. Carbon ion radiobiology[J]. Cancers (Basel), 2020, 12(10): 3022. DOI:10.3390/cancers12103022 |
| [2] |
Karger CP, Peschke P. RBE and related modeling in carbon-ion therapy[J]. Phys Med Biol, 2017, 63(1): 01TR02. DOI:10.1088/1361-6560/aa9102 |
| [3] |
Watson JD, Crick FH. Molecular structure of nucleic acids; a structure for deoxyribose nucleic acid[J]. Nature, 1953, 171(4356): 737-738. DOI:10.1038/171737a0 |
| [4] |
Chadwick KH, Leenhouts HP. A molecular theory of cell survival[J]. Phys Med Biol, 1973, 18(1): 78-87. DOI:10.1088/0031-9155/18/1/007 |
| [5] |
Elsässer T, Scholz M. Cluster effects within the local effect model[J]. Radiat Res, 2007, 167(3): 319-329. DOI:10.1667/RR0467.1 |
| [6] |
Elsässer T, Weyrather WK, Friedrich T, et al. Quantification of the relative biological effectiveness for ion beam radiotherapy: direct experimental comparison of proton and carbon ion beams and a novel approach for treatment planning[J]. Int J Radiat Oncol Biol Phys, 2010, 78(4): 1177-1183. DOI:10.1016/j.ijrobp.2010.05.014 |
| [7] |
Hawkins RB. A microdosimetric-kinetic theory of the dependence of the RBE for cell death on LET[J]. Med Phys, 1998, 25(7): 1157-1170. DOI:10.1118/1.598307 |
| [8] |
Hawkins RB. A microdosimetric-kinetic model for the effect of non-Poisson distribution of lethal lesions on the variation of RBE with LET[J]. Radiat Res, 2003, 160(1): 61-69. DOI:10.1667/rr3010 |
| [9] |
Rucinski A, Biernacka A, Schulte R. Applications of nanodosimetry in particle therapy planning and beyond[J]. Phys Med Biol, 2021, 66(24). DOI:10.1088/1361-6560/ac35f1 |
| [10] |
Carlson DJ, Stewart RD, Semenenko VA, et al. Combined use of Monte Carlo DNA damage simulations and deterministic repair models to examine putative mechanisms of cell killing[J]. Radiat Res, 2008, 169(4): 447-459. DOI:10.1667/RR1046.1 |
| [11] |
McMahon SJ, McNamara AL, Schuemann J, et al. A general mechanistic model enables predictions of the biological effectiveness of different qualities of radiation[J]. Sci Rep, 2017, 7(1): 10790. DOI:10.1038/s41598-017-10820-1 |
| [12] |
Wang W, Li C, Qiu R, et al. Modelling of Cellular Survival Following Radiation-Induced DNA Double-Strand Breaks[J]. Sci Rep, 2018, 8(1): 16202. DOI:10.1038/s41598-018-34159-3 |
| [13] |
Buglewicz DJ, Walsh KD, Hirakawa H, et al. Biological Effects of Monoenergetic Carbon Ions and Their Associated Secondary Particles[J]. Front Oncol, 2022, 12: 788293. DOI:10.3389/fonc.2022.788293 |
| [14] |
Faddegon B, Ramos-Méndez J, Schuemann J, et al. The TOPAS tool for particle simulation, a Monte Carlo simulation tool for physics, biology and clinical research[J]. Phys Med, 2020, 72: 114-121. DOI:10.1016/j.ejmp.2020.03.019 |
| [15] |
Semenenko VA, Stewart RD. A fast Monte Carlo algorithm to simulate the spectrum of DNA damages formed by ionizing radiation[J]. Radiat Res, 2004, 161(4): 451-457. DOI:10.1667/rr3140 |
| [16] |
Friedrich T, Ilicic K, Greubel C, et al. DNA damage interactions on both nanometer and micrometer scale determine overall cellular damage[J]. Sci Rep, 2018, 8(1): 16063. DOI:10.1038/s41598-018-34323-9 |
| [17] |
Friedrich T, Pfuhl T, Scholz M. Update of the particle irradiation data ensemble (PIDE) for cell survival[J]. J Radiat Res, 2021, 62(4): 645-655. DOI:10.1093/jrr/rrab034 |
| [18] |
Wenzl T, Wilkens JJ. Modelling of the oxygen enhancement ratio for ion beam radiation therapy[J]. Phys Med Biol, 2011, 56(11): 3251-3268. DOI:10.1088/0031-9155/56/11/006 |
| [19] |
Tsujii H, Kamada T, Shirai T, et al. Carbon-ion radiotherapy: principles, practices, and treatment planning[M]. Tokyo: Springer, 2014.
|
| [20] |
Furusawa Y, Fukutsu K, Aoki M, et al. Inactivation of aerobic and hypoxic cells from three different cell lines by accelerated 3He-, 12C-and 20Ne-Ion Beams[J]. Radiat Res, 2000, 154(5): 485-496. DOI:10.1667/0033-7587(2000)154[0485:ioaahc]2.0.co;2 |
| [21] |
Haettner E, Iwase H, Krämer M, et al. Experimental study of nuclear fragmentation of 200 and 400 MeV/u (12) C ions in water for applications in particle therapy[J]. Phys Med Biol, 2013, 58(23): 8265-8279. DOI:10.1088/0031-9155/58/23/8265 |
| [22] |
Francis Z, Seif E, Incerti S, et al. Carbon ion fragmentation effects on the nanometric level behind the Bragg peak depth[J]. Phys Med Biol, 2014, 59(24): 7691-7702. DOI:10.1088/0031-9155/59/24/7691 |
| [23] |
Underwood T, McNamara AL, Appelt A, et al. A systematic review of clinical studies on variable proton Relative Biological Effectiveness (RBE)[J]. Radiother Oncol, 2022, 175: 79-92. DOI:10.1016/j.radonc.2022.08.014 |
| [24] |
Mathews LA, Cabarcas SM, Hurt EM, et al. DNA repair pathways and mechanisms. DNA repair of cancer stem cells[M]. Berlin: Springer, 2013.
|
| [25] |
Henthorn NT, Warmenhoven JW, Sotiropoulos M, et al. Nanodosimetric simulation of direct ion-induced DNA damage using different chromatin geometry models[J]. Radiat Res, 2017, 188(6): 690-703. DOI:10.1667/RR14755.1 |
| [26] |
Nickoloff JA, Sharma N, Taylor L. Clustered DNA double-strand breaks: Biological effects and relevance to cancer radiotherapy[J]. Genes (Basel), 2020, 11(1): 99. DOI:10.3390/genes11010099 |
| [27] |
Karger CP, Glowa C, Peschke P, et al. The RBE in ion beam radiotherapy: In vivo studies and clinical application[J]. Z Med Phys, 2021, 31(2): 105-121. DOI:10.1016/j.zemedi.2020.12.001 |
| [28] |
Dai T, Li Q, Liu X, et al. Nanodosimetric quantities and RBE of a clinically relevant carbon-ion beam[J]. Med Phys, 2020, 47(2): 772-780. DOI:10.1002/mp.13914 |
 2024, Vol. 44
2024, Vol. 44


