2. 国科离子医疗科技有限公司, 北京 100190;
3. 香港理工大学医疗科技及资讯学系, 香港 999077;
4. 北京大学物理学院, 北京 100871;
5. 北京大学肿瘤医院暨北京市肿瘤防治研究所放疗科 恶性肿瘤发病机制及转化研究教育部重点实验室, 北京 100142
2. Department of Technology, CAS Ion Medical Technology Co., Ltd., Beijing 100190, China;
3. Department of Health Technology and Informatics, The Hong Kong Polytechnic University, Hong Kong 999077, China;
4. School of Physics, Peking University, Beijing 100871, China;
5. Key Laboratory of Carcinogenesis and Translational Research (Ministry of Education/Beijing), Department of Radiation Oncology, Peking University Cancer Hospital & Institute, Beijing 100142, China
与光子和电子相比,质子因其布拉格峰效应,可通过展宽调制实现剂量分布对肿瘤靶区的适形,在癌症治疗中具有潜在的物理和生物学优势[1]。临床上,质子的相对生物效能(RBE)受到辐射传能线密度(linear energy transfer,LET)、细胞内氧浓度等复杂因素的影响[2-3]。微观上,分子层级的径迹结构模拟可通过细致描述粒子在组织中的能量沉积过程,以有别于线性二次模型(linear-quadratic model,LQM)等数学模型的方法与技术路径计算质子的生物学效应,目前在GEANT4-DNA、TOPAS-nBio等蒙特卡罗软件中均已普遍应用。DNA是放射生物学效应的关键靶点[4],其损伤包括单链断裂(SSBs)和双链断裂(DSBs),后者更复杂而难以修复,是引发细胞凋亡的重要损伤[5]。DSB的判断依据一般在DNA双螺旋结构上的10个碱基对的长度上[6-7],因此DNA模型的微观结构直接影响DSB产率的模拟。GEANT4-DNA、TOPAS-nBio等软件中的DNA模型面临结构复杂且难以调整等问题[8-10]。考虑到DSB产率模拟依赖于纳米尺度上的DNA结构,上述问题可通过固定DNA宏观结构而调整微观结构参数解决。
本研究在gMicroMC代码框架中植入了均匀填充于球形细胞核的环状DNA分子,并编写了损伤查找算法计算不同核苷酸对间转角(以下简称转角)的模型中不同能量质子在细胞核中诱导的DSB产率。通过比较模拟结果,探究转角这一微观结构参数对质子生物学效应模拟的影响,并对标前人实验结果,以验证此简化DNA模型的应用潜力。该模型及思路有望应用于质子放疗计划系统的剂量计算模块,实现更灵活、高效的物理和生物模拟。
材料与方法1. DNA分子设计:构建了与pBR322质粒相同分子量(4 362碱基对)的环状双螺旋质粒DNA分子,作为细胞核中均匀填充的基本单元。质粒分子的双螺旋链骨架参照了Bernal等[11]于2015年提出的粗粒化B-DNA模型:结构基元为核苷酸对,每个核苷酸对中的碱基对等效建模为中心的一个底面半径0.5 nm、厚度0.34 nm的圆柱体,两个糖磷酸集团则分别等效于由外切且相对碱基对中心错开135°的两个半径为0.45 nm的球体。相邻核苷酸对关于垂直于对称面的轴(局部Z轴)旋转一定角度,通常依据双螺旋链的螺旋周期取为36°[11],但依DNA模型的具体选择而可有多样取值。本工作分别选取20°、30°、72° 3个不同角度构建了一组仿真细胞核DNA模型,以探究此微观结构参量对于相同质子束辐照下DSB产率模拟的影响。
2. 细胞核模型:细胞核定义为置于足够大的水模体中央、半径为2 750 nm的球体区域,在物理阶段视作填充与环境完全等同的水。细胞核中均匀分布有5 922个完全相同的质粒分子,碱基对总浓度为0.30 Mbps/μm3。由于DNA双链断裂的判据取10个碱基对长度内多于一个位点的链损伤,浓度对于双链断裂产率(定义为每Gy质子剂量、每单位DNA上产生的DSB数量)并无直接影响,因此综合考虑建模与模拟的运算效率选取了上述浓度。
3. 蒙特卡罗模拟工具:本工作构建的质粒DNA模型的有关算法基于Lai等[12]开发的基于GPU并行计算加速的gMicroMC代码框架编写,其基础代码在GitHub上开源,采用CMake联合nvcc编译,并在Ubuntu终端中调用命令执行。本研究中大部分可调参数,如反应概率、电子截止能量等皆沿用了Lai等[12]文章中的取值,并行计算时为每个block分配256个线程,用131 072总线程数保证模拟计算时不发生下标越界。gMicroMC通过计算质子径迹结构获取水分解过程产生的次级粒子扩散及与DNA相互作用等信息,其模拟通常分为4个阶段:物理阶段(10-15~10-12s),确定能量沉积位置和初始电离或激发的水分子;物理化学阶段(10-12s),给出自由基的初始位置和类型;化学阶段(10-12~10-6s),处理自由基扩散和相互反应,最后在DNA阶段中查找并统计不同复杂度的DNA损伤。
计算质子LET采用的TOPAS MC软件为官网发布的3.9版本,安装包为适用于Debian 9、10及Ubuntu 18、19、20等系统的源码。模拟计算时选择适用于质子径迹模拟的g4em-standard_opt3(即Geant4中的G4EMStandardPhysics_option3) 物理模组。
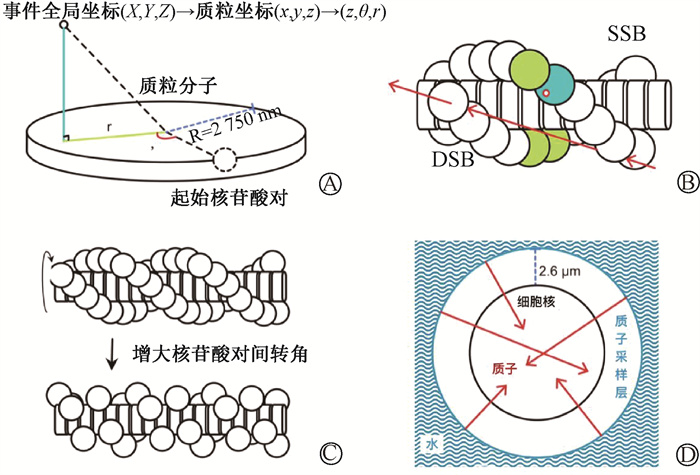
4. DNA损伤查找算法:在化学阶段和DNA阶段,通过检查能量沉积事件或自由基在扩散过程中是否落入质粒分子中的糖磷酸基团(外扩反应半径Rp或Rc)来判定DNA断裂是否可能发生,断裂发生的概率沿用gMicroMC中的线性概率损伤模型。gMicroMC基于CUDA编程,对于质粒模型,每个GPU线程处理一个物理事件或自由基,并在该线程内迭代所有质粒分子,查找潜在重叠,基于反应概率判断损伤位点。质粒作为基元的空间坐标由3个float3变量定义:质粒中心位置矢量center、单位法向量normal和0号碱基对相对于质粒中心的方向向量R0。坐标通过MATLAB计算得到,采样时遍历已填充的质粒分子判断是否存在交叠,若有则重新采样,直到质粒分子间互不重叠,并填充到预期浓度为止。当每个线程处理一个事件并迭代每个质粒时,事件的全局坐标首先转换为质粒下的局部坐标(图 1A),引入一组三维基底描述事件坐标相对于各质粒的位置:垂直高度z、相对于原始碱基对的旋转角度θ和径向坐标r。角度θ确定了碱基对及其4个最近糖磷酸基团的位置,分别计算事件坐标与上述5个粗粒化结构中心的有效距离(定义为几何中心与事件的直线距离减去基团半径与反应半径)。如果最小有效距离为负且发生于某一糖磷酸集团,则遵从gMicroMC默认的算法生成一个随机数,并根据相应的反应概率确定是否发生单链断裂。
|
图 1 DNA模型结构与质子采样示意 A. 能量沉积事件或羟自由基的空间全局笛卡尔坐标与质粒坐标的转换关系;B. 单链断裂(SSB,红色空心点)与双链断裂(DSB,红色箭头) 示例;C. DNA双螺旋链结构随转角增加时发生的变化;D. 细胞核外质子采样的方式 Figure 1 DNA and radiation models used in this work A. Transformation of global Cartesian coordinates of energy deposition events or hydroxyl radical termination points to plasmid coordinates; B. Examples of single-strand breaks (SSB, red hollow dot) and double-strand breaks (DSB, red arrow); C. Structural changes in the DNA helix with increased dihedral angles; D. Illustration of proton sampling outside the nucleus |
物理阶段能量沉积事件的能量超出阈值17.5 eV且在糖磷酸基团反应范围内的事件会导致单链断裂。在化学阶段,羟基自由基在扩散过程中若落入反应范围内也会导致单链断裂,即产生单个SSB。如果10个碱基对范围内存在超过两个SSB,则构成双链断裂(图 1B)。判定为两独立链断裂的最小间隔、损伤的复杂度沿用gMicroMC的定义,在本工作中只考虑不同复杂度DSB的总额。
5. 质子在不同转角的质粒模型中的DSB产率模拟:在MATLAB中分别构建了转角为20°、36°、72°的3种质粒分子(图 1C)。角度值的选取仅用于反映模型差异。在gMicroMC中对上述3个模型分别采用0.5、1、3、6、10、20 MeV 6个不同初始动能的质子照射(图 1D),其中质子的初始位置从与细胞核同中心的半径为2.6 μm的球壳上均匀采样,等效于质子照射2.6 μm厚的水层下方的细胞。gMicroMC中预设了目标剂量,质子束将依照设定的单次出束粒子数不断照射,直到在2 750 nm半径的球体,即剂量计算的区域中剂量达到预设值。记录中包含单次出束后累积的剂量,以及此时不同复杂度的DNA损伤数目。每次出束后的结果取重复5次后统计损伤平均值,以减少随机误差。因细胞核内DSB产额在达到饱和前与剂量存在线性关系,本研究中的目标剂量取为230 Gy左右,未到达饱和且拟合效果较好,拟合斜率即为当次照射实验中的DSB产率。为对比不同模型的模拟结果以验证转角对DSB产率计算的影响,每个模型分别对6个能量的质子进行12次模拟,在SPSS中进行描述性统计,并计算组间相对差异。
6. 3种模型下RBE与质子LET的关系及模型准确性比较:为了进一步比较3个模型对相对生物学效应的模拟效果,在TOPAS MC中对本研究采用的细胞核建模,即在足够大的水箱中心圈划一个半径为2 750 nm的球形水,用作细胞核的等效替代,质子束设定为光斑较小的平行光,从(0, 0, -5 350 nm)沿Z轴向细胞核中心即世界原点出射(图 1D)。细胞核区域内质子的LET由TOPAS MC中的ProtonLET计数卡片计算给出,对于每种模型与质子能量的组合,进行足够多次重复模拟以使得细胞核内质子LET收敛到比较准确的值,本研究将每个模型在各个能量下模拟的总粒子数定为8×105,RBE值定义为某种能量下质子DSB产率与参考射线60Co的γ光子在仓鼠肺细胞(V79)中诱导的DSB总产率之比值,其中后者参考了Hsiao等[13]给出的实验结果8.1×10-11·Gy-1· Gbps-1。为进行对比验证,利用TOPAS MC提供的Proton RBE Scorer扩展包[14]计算若干RBE模型下上述细胞核模型在不同质子LET下对应的RBE值,结合Matsuya等[15]汇集的V79细胞系在10%生存率下不同质子LET对应的RBE实验测量值,对比不同转角的质粒模型对于相对生物学效应的模拟效果。
7. 数据处理与硬件配置:本研究中所有步骤皆在Ubuntu 20.04.5 LTS(GNU/Linux 5.4.0-128-generic x86_64) 中完成。GPU选用NVIDIA RTX A5000显卡,驱动版本530.30.02,CUDA版本12.1;采用MATLAB 2022处理gMicroMC的原始数据,拟合得到各次模拟实验的DSB产率;采用OriginPro 2023b作图;在IBM SPSS Statistics 26中,对不同模型在不同能量质子照射下DSB的产率进行统计分析。
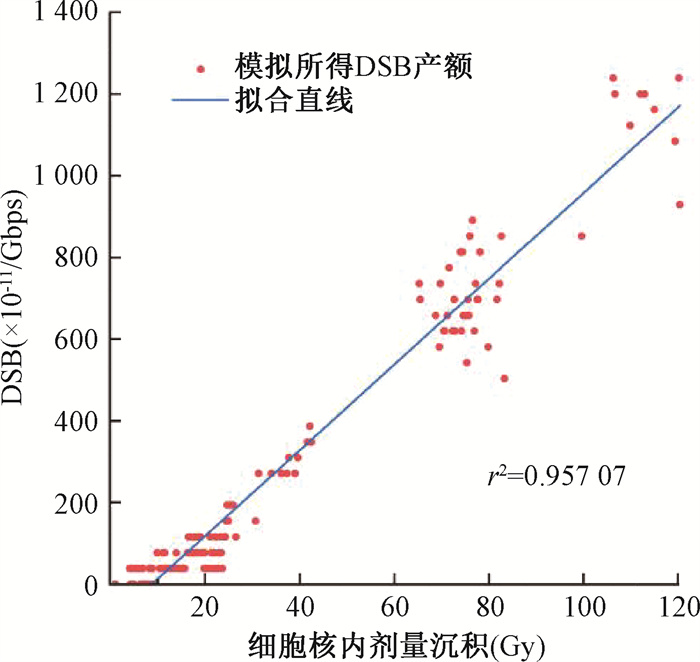
结果1. DSB产率计算:通过gMicroMC获得各次出束后细胞核内累计的剂量沉积,及对应的不同复杂度DNA链断裂的产额。在MATLAB中将DSB总产额对剂量进行线性拟合(图 2)。当次模拟的DSB产率定义为拟合后的斜率,10-11·Gy-1·Gbps-1。
|
图 2 20 MeV质子照射时随细胞核内剂量沉积每Gbps质粒DNA中双链断裂的含量及拟合直线示意 Figure 2 Dose-dependent DNA double-strand break induction in plasmid DNA per Gbps under 20 MeV proton exposure with fitted linear regression |
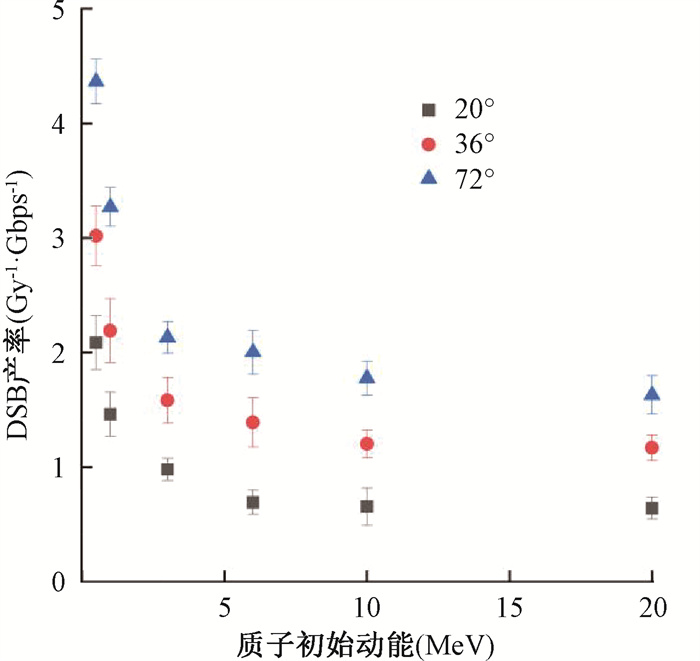
2. 各模型下不同能量的质子诱导的DSB产率:将转角分别为20°、30°、72°的3种质粒填充的细胞核模型中6个不同能量的质子照射下DSB产率与质子初动能的依赖关系绘制为箱线图(图 3)。可见对于每个模型,随质子初始动能增加,DSB产率呈现出总体下降趋势,且下降的幅度减缓。这一现象与基于质子深度剂量曲线得到的预期相符:对于本工作采用的细胞核照射模型,由于1 MeV以上的质子射程已超过10 μm[16],剂量的布拉格峰出现在细胞后,即细胞内质子的剂量落在质子的剂量深度曲线布拉格峰以前的单调增长区,使得初始能量越大,质子在细胞核区域内的剂量距离布拉格峰越远,能量沉积率越低,DSB产率相应地越低。各能量下的误差来自模拟时GPU硬件的性能与拟合误差。
|
图 3 不同转角的DNA模型在不同能量质子照射下的DSB产率 Figure 3 DSB yields mduced by proton radiaton with varying energies in DNA models with different dihedral angles |
对于不同模型,随着转角的增大,质子DSB产率在各个能量下都显现出升高的趋势。这一现象与糖磷酸集团的空间分布有关:相邻核苷酸对中的糖磷酸集团彼此间存在一定重叠,在计算时取中心与位点距离较近者记录损伤;由于转角从一个较小的取值开始逐渐增大时,糖磷酸集团在中心碱基对骨架外侧分布得更加松散,彼此之间交叠减少,占据的总体积增大,使得质子径迹上更容易发生多次穿透糖磷酸集团导致单链损伤的现象,因而双链断裂的概率也相应增大。
表 1给出了不同模型中模拟结果两两比较下均值的相对差异。由于不同能量质子的DSB产率绝对数值在3个模型中的大小关系完全相同,即转角72°>36°>20°,因此表格仅展示两组模型中模拟结果的相对差异。组间差异百分比的计算公式为:
| $ \mathit { difference }=\frac{Y_{\mathrm{DSB}}^{\prime}-Y_{\mathrm{DSB}}}{Y_{\mathrm{DSB}}} \times 100 \% $ | (1) |
|
|
表 1 不同转角各能量质子DSB产率在不同模型中的组间差异 (%) Table 1 Inter-model differences in DSB yields under proton radiation with different energies under different twist angels (%) |
式中,YDSB为转角取20°(或36°)时模型中的质子DSB产率,YDSB′为转角取36°(或72°)时模型中的质子DSB产率。由表 1可得,各能量质子在不同模型中的DSB产率相对差异均在34.6%以上,可见模型转角对DSB产率的模拟结果具有重要影响。
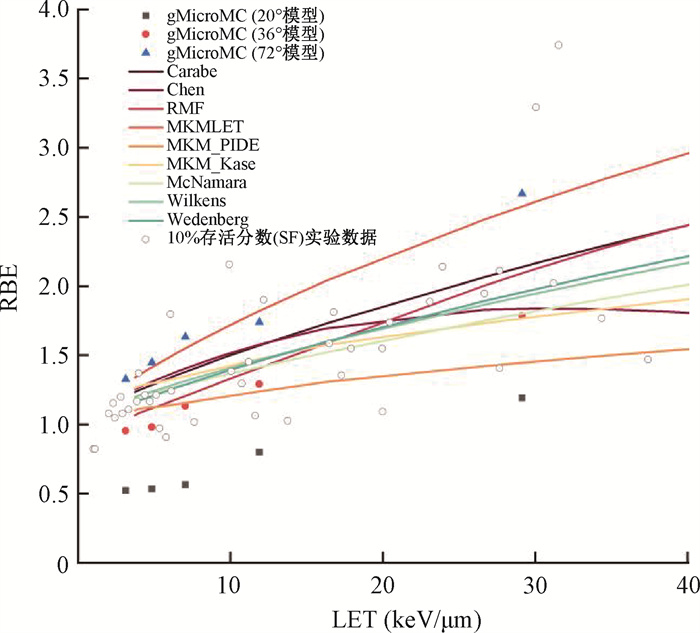
3. 质子在不同LET下的RBE:在TOPAS MC中计算各初始动能的质子在不考虑质粒的纯水模型(与gMicroMC中几何设定一致)中细胞核区域内的LET。初始动能分别为0.5、1.0、3.0、6.0、10.0及20.0 MeV的质子,在模型中的LET值分别为62.60、29.13、11.89、7.04、4.84与3.12 keV/μm。将计算得到的各模型下不同LET质子的RBE与TOPAS MC中质子RBE扩展包计算得到的RBE-LET变化曲线、前人在R79细胞系上进行的模拟结果进行比较(图 4)。可见,在3种模型与涉及的质子能量中,质粒分子转角取为72°时,gMicroMC的模拟结果与MKM-LET模型吻合较好;而参考数据总体上落在36°与72°两个模型之中,说明对于该转角的选取或可进一步在这个角度范围内进行考察。需要强调的是,由于RBE的计算具有较高的任意性,如参考射线、生物学效应终点的不同选择都将影响RBE的数值。通过比较基于DSB产率计算的RBE和其他模型以细胞存活率为终点的RBE,可验证基于质粒模型的DSB产率模拟用于质子RBE计算的合理性。
|
注:彩色实心散点为gMicroMC在3种质粒模型中的模拟结果,灰色空心圆为仓鼠肺细胞V79在10%生存率定义下的RBE实验值,彩色曲线为TOPAS MC中基于本工作的细胞核模型模拟计算的RBE-LET关系 图 4 转角不同的3个DNA模型中的质子DSB产率随LET的变化关系 Figure 4 relationship between proton DSB yields and LET in three DNA models with different dihedral angles |
讨论
由于质子的布拉格峰效应、高水平的活性氧及γ-H2AX产量,表现出与电子、光子不同的生物学效应,且受到组织氧含量等众多因素的影响,一般的含参物理模型很难有效对其生物学效应进行系统描述。径迹结构蒙特卡罗模拟因为能够从基本物理反应出发,忠实描述粒子在射程内轨迹的精细微观结构,可更精确地计算质子的生物学效应。DNA是放射损伤的主要靶点,合适的DNA模型在径迹结构模拟中扮演着至关重要的角色。基于DNA损伤的微观机制,本研究提出了一种将DNA分子的宏观与微观结构相互分离的简单质粒模型,仅通过调节相邻核苷酸对之间的转角这一微观参量,即可改变细胞核模型在射线照射下的响应,通过选取合适的微观结构即可通过DSB产率反映真实细胞系在射线辐照下的生物学效应。本工作基于的gMicroMC框架创新性利用了GPU加速,同时质粒模型的对称性与低自由度也便于分线程并行计算以提高运算效率。
质子的RBE一般取1.1[17],但通过模拟不同LET下的RBE值,可见RBE对于LET表现出了极强的依赖;由于质子LET与射线穿过的组织成分有关,说明质子治疗计划设计中精确的物理模拟至关重要。
本研究初步探究了单一微观结构变量对模型的调整,发现基于3个不同转角的质粒模型对初始动能0.5~20 MeV的质子辐照响应表现出了显著的差异;而RBE随LET的变化及与其他模型或实验结果的对标表明,当转角选为36°至72°之间的某个值时,质粒模型能够更有效地反映真实细胞(如V79细胞系)中质子的生物学效应,这个更优值可通过选定某种射线的DSB产率作为金标准后,将不同转角对应的质粒模型中该射线的DSB产率进行合适的拟合,得到最优的转角取值。
通过质子或电子、光子的物理模拟确定一个最符合某种或某些射线实际效应的模型后,未来的工作还将探究本质粒体系在其他能量范围内的质子、α粒子及重离子照射下的物理模拟效果。考虑到放射生物学效应同时受制于剂量率、氧含量等因素,未来还将基于gMicroMC对本模型进一步开发,如在化学阶段考虑质粒模型中各化学物种浓度的影响,对模型的其他可变微观参数(如反应半径等)进行即时调整。此外,碳离子辐照实验等生物学实验结果未来也将用作物理模拟的对标,以对模型进行多维度验证。
本研究提出的简化质粒模型通过分离复杂的宏观结构,进而完全采用微观结构对体系进行描述,相比现有的一般细胞核DNA模型在建模与运算效率上皆有所改善。本模型有望应用到未来质子治疗的计划设计中:如基于双能量CT等体素化成像获取患者体内不同组织的密度和成分分布,并转换为模型中的质粒参数分布,即可将真实组织基于质粒模型进行等效替代,进而提升质子放疗计划设计中生物学剂量模拟计算的灵活性和高效性。
利益冲突 无
志谢 感谢兰州重离子研究装置(HIRFL)提供实验条件
作者贡献声明 华凌负责模型设计、编写程序、实施研究、采集并整理数据、统计分析、撰写论文;赖有方指导并参与部分模型设计与实验设计;孔祥慧、黎田、张艺宝负责指导模型与实验设计、修改论文;林晨、胡俏俏指导数据处理、修改论文
| [1] |
de Vera P, Abril I, Garcia-Molina R. Energy spectra of protons and generated secondary electrons around the Bragg peak in materials of interest in proton therapy[J]. Radiat Res, 2018, 190(3): 282-297. DOI:10.1667/RR14988.1 |
| [2] |
Iwata H, Ogino H, Hashimoto S, et al. Spot scanning and passive scattering proton therapy: relative biological effectiveness and oxygen enhancement ratio in cultured cells[J]. Int J Radiat Oncol Biol Phys, 2016, 95(1): 95-102. DOI:10.1016/j.ijrobp.2016.01.017 |
| [3] |
Ganjeh ZA, Eslami-Kalantari M, Loushab ME. Study of the RBE depth dependence of protons using a damage diagnostic algorithm and its application in proton therapy based on Monte Carlo simulation[J]. J Instrum, 2021, 16(12): P12027-1-P12027-16. DOI:10.1088/1748-0221/16/12/P12027 |
| [4] |
Gray LH. Actions of radiations on living cell, 1946 and after the second Douglas Lae memorial lecture[J]. Br J Radiol, 1952, 25(293): 235-244. DOI:10.1259/0007-1285-25-293-235 |
| [5] |
Tounekti O, Kenani A, Foray N, et al. The ratio of single-to double-strand DNA breaks and their absolute values determine cell death pathway[J]. Br J Cancer, 2001, 84(9): 1272-1279. DOI:10.1054/bjoc.2001.1794 |
| [6] |
Shamsabadi R, Baghani HR. An inter-comparison between radiobiological characteristics of a commercial low-energy IORT system by Geant4-DNA and MCDS Monte Carlo codes[J]. Int J Radiat Biol, 2024, 100(8): 1226-1235. DOI:10.1080/09553002.2023.2295290 |
| [7] |
Yoshii Y, Sasaki K, Matsuya Y, et al. Cluster analysis for the probability of DSB site induced by electron tracks[J]. Nucl Instrum Methods Phys Res Sect B, 2015, 350: 55-59. DOI:10.1016/j.nimb.2015.03.025 |
| [8] |
Meylan S, Vimont U, Incerti S, et al. Geant4-DNA simulations using complex DNA geometries generated by the DnaFabric tool[J]. Comput Phys Commun, 2016, 204: 159-169. DOI:10.1016/j.cpc.2016.02.019 |
| [9] |
Delage E, Pham QT, Karamitros M, et al. PDB4DNA: implementation of DNA geometry from the Protein Data Bank (PDB) description for Geant4-DNA Monte-Carlo simulations[J]. Comput Phys Commun, 2015, 192: 282-288. DOI:10.1016/j.cpc.2015.02.026 |
| [10] |
Schuemann J, McNamara AL, Ramos-Méndez J, et al. TOPAS-nBio: an extension to the TOPAS simulation toolkit for cellular and sub-cellular radiobiology[J]. Radiat Res, 2019, 191(2): 125-138. DOI:10.1667/RR15224.1 |
| [11] |
Bernal MA, deAlmeida CE, Incerti S, et al. The influence of DNA configuration on the direct strand break yield[J]. Comput Math Methods Med, 2015, 2015: 417501. DOI:10.1155/2015/417501 |
| [12] |
Lai Y, Tsai M, Tian Z, et al. A new open-source GPU-based microscopic Monte Carlo simulation tool for the calculations of DNA damages caused by ionizing radiation-Part I: Core algorithm and validation[J]. Med Phys, 2020, 47(4): 1958-1970. DOI:10.1002/mp.14096 |
| [13] |
Hsiao YY, Chen FH, Chan CC, et al. Monte Carlo simulation of double-strand break induction and conversion after ultrasoft X-rays irradiation[J]. Int J Mol Sci, 2021, 22(21): 11713. DOI:10.3390/ijms222111713 |
| [14] |
Polster L, Schuemann J, Rinaldi I, et al. Extension of TOPAS for the simulation of proton radiation effects considering molecular and cellular endpoints[J]. Phys Med Biol, 2015, 60(13): 5053-5070. DOI:10.1088/0031-9155/60/13/5053 |
| [15] |
Matsuya Y, Kai T, Parisi A, et al. Application of a simple DNA damage model developed for electrons to proton irradiation[J]. Phys Med Biol, 2022, 67(21). DOI:10.1088/1361-6560/ac9a20 |
| [16] |
Alcocer-Ávila ME, Quinto MA, Monti JM, et al. Proton transport modeling in a realistic biological environment by using TILDA-V[J]. Sci Rep, 2019, 9(1): 14030. DOI:10.1038/s41598-019-50270-5 |
| [17] |
Jones B. Clinical radiobiology of proton therapy: modeling of RBE[J]. Acta Oncol, 2017, 56(11): 1374-1378. DOI:10.1080/0284186X.2017.1343496 |
 2024, Vol. 44
2024, Vol. 44


