2. 中南大学湘雅医院肿瘤科, 长沙 410008;
3. 安徽慧软科技有限公司, 合肥 230026;
4. 中国科学技术大学附属第一医院放疗科, 合肥 230026
2. Xiangya Hospital Central South University, Department of Oncology, Changsha 410008, China;
3. Anhui Wisdom Technology Co., Ltd, Hefei 230026, China;
4. First Affiliated Hospital of University of Science and Technology of China, Department of Radiation Oncology, Hefei 230026, China
放射性核素药物治疗(RPT)最初于20世纪40年代初提出,甲状腺疾病的131I治疗是RPT临床最常见的应用[1]。与外照射疗法不同,177Lu-DOTATATE等RPT药物将放射性核素与能够靶向肿瘤相关受体的配体偶联可以特异性结合肿瘤以及其转移病灶,提供全身范围内的靶向治疗,且对正常组织造成的损害较小。药物在体内的分布受患者体型、病情进展、代谢能力等多个因素均影响。然而,现有治疗方案患者给药活度与周期固定,可能存在治疗不足或过度治疗的风险[2-3]。基于正电子发射计算机断层扫描(PET/CT)和单光子发射计算机断层扫描(SPECT/CT)等影像的直接蒙特卡罗(MC)模拟被认为是患者个体化剂量计算的金标准[4-6],然而计算效率限制了MC方法的应用。通用图形处理单元(GPU)的引入大大提高了MC方法效率[7-11]。基于GPU的专用MC代码ARCHER已应用于多个临床医学物理场景[12-15]。近期,Peng等[16]开发的ARCHER-NM将ARCHER扩展到核医学影像领域。本研究将ARCHER-NM的研究拓展到67Cu、89Sr、90Y、131I、177Lu及188Re等RPT常用核素中,通过与通用MC程序GATE水模体剂量的对比来验证ARCHER-NM对多种β放射性核素剂量计算的准确性以及泛用性,并进一步以两例177Lu-DOTATATE治疗患者剂量计算结果及效率的对比,验证ARCHER-NM在放射性核素治疗个体化剂量计算中的应用潜力。
材料与方法1. 模拟实验设计:首先,设计水模体实验以验证ARCHER-NM在不同放射性核素剂量计算上的准确性与泛用性。分别创建体素间距为4 mm × 4 mm × 4 mm,分辨率51 × 51 × 51的CT和SPECT图像。CT图像中的所有体素赋值为0作为水模体。SPECT图像中心体素赋值为1作为中心点源。本研究水模体验证实验涉及的放射性核素包括67Cu、89Sr、90Y、131I、177Lu及188Re。所有水模体模拟实验中ARCHER-NM与GATE衰变粒子数均为5 × 107。
在上述水模体实验的基础上,以密歇根大学公开数据集[17]提供的患者数据为例,进行个体化放射性核素治疗剂量计算验证ARCHER-NM应用于该临床场景的可行性。患者一般资料及病灶基本情况如下:患者1为64岁男性,身高175.3 cm,体重93 kg,注射177Lu-DOTATATE 7.21 GBq后4、28、100、120 h分别进行SPECT/CT图像采集。共两个病灶:分别位于肝右叶(病灶1)和肝左叶(病灶2),体积分别为107.46和2.84 cm3,治疗前PET成像SUVpeak分别为26.07和28.63;患者2为62岁女性,身高162.6 cm,体重51.7 kg,注射177Lu-DOTATATE 7.31 GBq后4、33、100、194 h进行图像采集。共4个病灶:分别位于肝右叶(病灶1)、肝左叶(病灶2)、胰头周围淋巴结(病灶3)以及胸壁(病灶4),体积分别为10.44、2.98、67.72和22.88 cm3,治疗前PET成像SUVpeak为10.74、47.35、32.27和20.69 cm3。
数据集包括两例患者的以下信息:患者治疗前PET图像、多时间点SPECT/CT、患者病灶、肾、肝、脾等器官分割结果以及基于上述SPECT图像数据由MIM(美国MIM软件有限公司)经指数拟合方法得到的时间积分活度(TIA)图等。SPECT/CT图像采集均在德国西门子Intevo系统执行,SPECT图像分辨率为256 × 256 × 199,体素间距1.953 mm ×1.953 mm ×1.953 mm。使用xSPECT Quant重建,图像单位为Bq/ml;TIA图像分辨率与SPECT图像一致,单位为Bq·ml-1·s。
由TIA图像获取放射源强度和空间分布信息,对CT进行重采样并对齐至TIA图像,根据重采样CT生成患者个性化体模用于剂量计算,模拟衰变事件数为5 × 109。使用自主研发的基于深度学习的器官自动勾画软件DeepViewer(安徽慧软科技有限公司)[18-19],基于患者CT数据对肺、脊髓、肠、膀胱等器官进行补充分割。靶区及各危及器官分割结果用于器官剂量结果分析。
2. ARCHER-NM设置:ARCHER-NM的主要工作流程和基于GPU的粒子输运方法之前工作中已经详细介绍并验证[12-13, 16],采用批量统计误差估计方法[20]来评估不确定度。核素衰变产物及分支比参考国际放射防护委员会(ICRP)107报告[21],能谱中产额 < 1 ×10-4的部分剂量贡献太小不予考虑。光子与电子截止能量分别设置为10与40 keV。三维剂量结果与输入CT图像保持相同的大小和分辨率。
ARCHER-NM在Windows 10计算机系统运行。硬件配置为GPU-Nvidia Titan RTX显卡,24 GB显存,CPU-Intel® CoreTMi7-7700 @ 3.60GHz,32 GB内存。
3. GATE设置:本研究使用基于通用MC软件Geant 4(v11.0)的用户软件GATE(v9.2)。输入CT和SPECT图像设置与ARCHER-NM相同。放射性核素源调用Geant4软件放射性衰变物理模块生成。使用物理模型emstandard_opt3[22]处理电磁输运,次级光子、电子产生阈值分别设为1和0.45 mm。DoseActor计数器用于记录吸收剂量。
GATE模拟实验在Linux服务器上运行,服务器硬件配置为:CPU:Intel® Xeon® Gold 6348 3.50 GHz,56核,112线程,总共256 GB内存。为了尽可能提高GATE的计算速度,模拟实验均使用100个进程并行执行。软件包gatetools用于合并所有进程的吸收剂量和不确定性等结果。
4. 数据提取与处理:水模体模拟实验中,使用以点源为中心指定边长立方体区域内的平均剂量以及点源的剂量-距离曲线评估GATE和ARCHER-NM剂量分布。放射性核素点源放置在水模体中心,在三维剂量分布中,以点源位置为原点,沿X轴提取吸收剂量数据,绘制剂量-距离曲线。
患者剂量分布计算中,模拟得到的三维剂量分布除以模拟粒子总数获得单次衰变平均剂量图,再乘以TIA图提供的患者全身累积衰变次数获得患者累积吸收剂量AD(Gy)。公式如下
| $ A D=\frac{D_{\text {sim }}}{N_{\text {event }}} \times A_{\text {total }} $ | (1) |
式中,Dsim为MC模拟总吸收剂量,Gy;Nevents为MC模拟中衰变事件总数;Atotal为患者周期累积衰变事件数,Bq·s。
基于上述累积吸收剂量与器官分割结果计算器官平均剂量ADmean与相应的器官不确定性ε的计算公式如下[24]:
| $ A D_{\text {mean }}=\frac{1}{N} \sum\limits_{i=1}^N A D_i $ | (2) |
| $ \varepsilon=\frac{1}{N} \sum\limits_{i=1}^N \varepsilon_i^2 $ | (3) |
式中,N为器官包含体素数;ADi和εi分别为体素i的吸收剂量与统计不确定度。
采用3D Gamma分析评估ARCHER-NM与GATE患者剂量计算结果的一致性,Gamma通过率计算标准为2 mm/1%,参考数据为当前体素剂量,忽略低于最大剂量3%的数据点,Gamma通过率γ(rm)计算公式如下[25]:
| $ \gamma\left(r_{\mathrm{m}}\right)=\min \left\{\Gamma\left(r_{\mathrm{m}}, r_{\mathrm{c}}\right)\right\} \forall\left\{r_{\mathrm{c}}\right\} $ | (4) |
| $ \Gamma\left(r_{\mathrm{m}}, r_{\mathrm{c}}\right)=\frac{r^2\left(r_{\mathrm{m}}, r_{\mathrm{c}}\right)}{\Delta d_{\mathrm{M}}^2}+\frac{\delta^2\left(r_{\mathrm{m}}, r_{\mathrm{c}}\right)}{\Delta D_{\mathrm{M}}^2} $ | (5) |
ARCHER-NM与GATE剂量的相对百分差异(Diff)计算公式如下:
| $ \text { Diff }=\frac{\text { Dose }_\text{A}-\text { Dose }_\text{G}}{\text { Dose }_\text{G}} \times 100 $ | (6) |
式中,DoseA为ARCHER-NM剂量;DoseG为GATE剂量。
结果1. 水模体剂量:图 1分别展示了67Cu、89Sr、90Y、131I、177Lu及188Re等6种点源在水模体中的吸收剂量-距离曲线,横坐标为剂量记录点到点源的距离,纵坐标为核素单次衰变平均吸收剂量。对于所有核素,吸收剂量在距离源16 mm之后降低到原点的万分之一,其中由于89Sr、90Y衰变产物以电子为主,射程较短,吸收剂量-距离曲线在尾部存在统计不确定性导致的波动;其他核素衰变均产生光子, 较电子输运距离更长,吸收剂量-距离曲线尾部趋势稳定。总体来看,ARCHER-NM与GATE吸收剂量-距离曲线一致性较好。以放射源为中心边长24 mm立方体区域内ARCHER-NM和GATE平均剂量、相对百分差异及计算时间并汇总于表 1。所有核素平均剂量相对差异在-1.63%~2.29%范围内,差异平均绝对值1.15%。综合图 1与表 1,ARCHER-NM与GATE在所有核素剂量计算中均表现出良好的一致性。
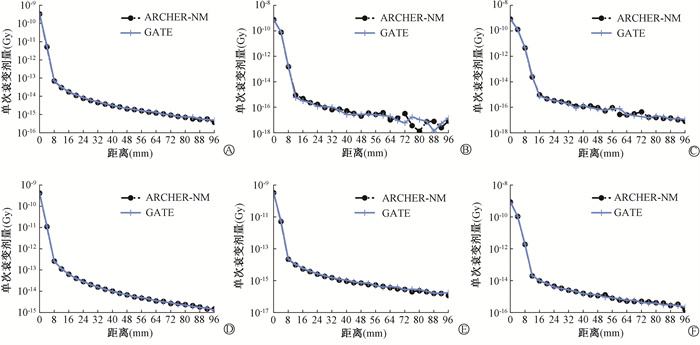
|
图 1 不同放射性核素点源在水模体的吸收剂量-距离曲线 A. 67Cu; B. 89Sr; C. 90Y; D. 131I; E. 177Lu; F. 188Re Figure 1 Absorbed dose-distance curves of different radionuclide point sources in water phantoms A. 67Cu; B. 89Sr; C. 90Y; D. 131I; E. 177Lu; F. 188Re |
|
|
表 1 不同点源为中心立方体水模体中ARCHER-NM和GATE的区域平均剂量比较 Table 1 Comparison of regional average doses in cubic water phantoms centered on different point sources between ARCHER-NM and GATE |
计算效率上,模拟5×107次衰变GATE需要运行254至965 s不等,平均运行时间556 s。同样任务量下,ARCHER-NM均在5 s内完成,平均运行时间3.3 s。保证计算结果精确的前提下,水模体剂量计算场景下ARCHER-NM能够比GATE快60至300倍。
2. β核素治疗患者个体化剂量:在上述水模体实验结果的支撑下进行患者个体化剂量计算。根据患者第一个时间点的CT图像进行危及器官勾画,具体结构因患者CT扫描范围及个人病史略有不同。患者1 CT扫描起于乳头连线,止于骨盆入口。除数据集提供的病灶、肝脏、两肾以及脾脏外,补充勾画得到胃、十二指肠、脊髓、肠道的轮廓。患者2 CT扫描范围起于乳头连线,止于股骨头,CT图像显示患者无脾脏。除数据集提供的病灶、肝脏、两肾外,补充进行腹部及盆部器官勾画得到胃、十二指肠、脊髓、肠道、膀胱、直肠的轮廓。
ARCHER-NM和GATE的器官平均剂量及相对差异汇总于表 2(空气剂量指定为0),所有器官的统计不确定度均 < 4%,病灶及肝、两肾、脾的统计不确定度均 < 2%。两患者病灶及平均剂量>1 Gy危及器官的DVH见图 2。患者1病灶2治疗前68Ga-DOTATATE PET成像SUVpeak较病灶1略高,体积远小于病灶1。从核素治疗剂量来看,病灶2平均剂量30.5 Gy远高于病灶1(21.32 Gy)。同样地,患者2所有病灶中,病灶2体积最小然而SUVpeak最高为47.35,其平均剂量约30 Gy,也远超其他病灶(均 < 5 Gy)。该现象提示药物在病灶之间并不按照体积均匀分布,剂量往往集中在SUVpeak较高的区域。根据患者病灶位置不同,危及器官高剂量区辐射范围也存在差异。患者2较患者1,由于胰头周围淋巴结以及胸壁转移灶的存在,十二指肠以及胃吸收剂量明显增加,此外,两肾平均剂量增大2 Gy。
|
|
表 2 ARCHER-NM与GATE两例177Lu-DOTATATE患者器官平均剂量与相对差异 Table 2 Average organ doses and relative differences between ARCHERNM and GATE in two patients treated with 177Lu-DOTATATE |
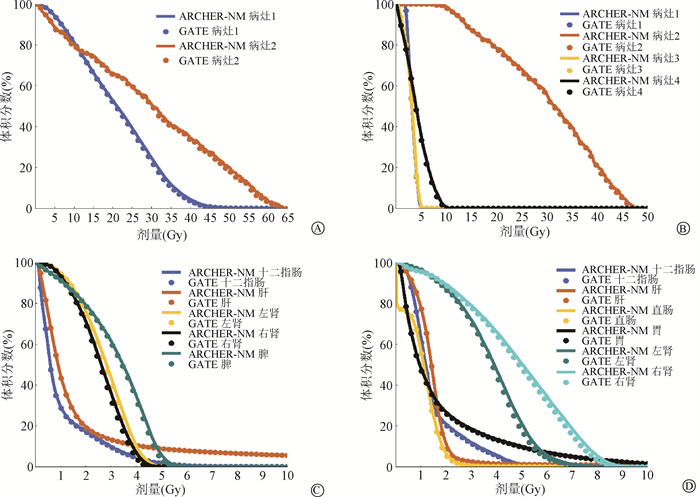
|
注:病灶1为肝右叶;病灶2为肝左叶;病灶3为胰头周围淋巴结;病灶4为胸壁 图 2 患者病灶及危及器官DVH A. 患者1病灶DVH;B. 患者1危及器官DVH图;C. 患者2病灶DVH;D. 患者2危及器官DVH图 Figure 2 DVHs for patients′ lesions and organs at risk A. DVH for patient 1′s two lesions; B. DVH for patient 1′s organs at risk; C. DVH for patient 2′s four lesions; D. DVH for patient 2′s organs at risk |
从图 2来看,ARCHER-NM与GATE的病灶与危及器官DVH曲线基本一致。表 2中ARCHER-NM与GATE所有器官的平均剂量相对差异为-3.83%~2.85%,所有器官平均剂量相对差异绝对值的平均值为1.91%。两患者ARCHER-NM与GATE剂量在3%等剂量线内2 mm/1% Gamma通过率分别为98.6%和98.8%。总的来说,ARCHER-NM与GATE患者剂量计算结果一致性很高。此外,完成患者剂量计算GATE计算所需时间均为9 h以上,而ARCHER-NM仅需要90 s左右,比GATE快350倍以上。
讨论目前RPT临床治疗方案多采用标准方案,即固定患者给药活度与周期。然而患者体型、病情进展、代谢能力、肿瘤细胞表面受体表达等多个因素均会影响药物在体内的分布。本研究中两例患者均采用标准治疗方案。然而根据剂量计算结果可以发现,不同患者、不同病灶之间吸收剂量差异巨大。患者个体化治疗检测和治疗设计可以一定程度上降低治疗不足或过度治疗的风险,快速准确的患者个体化剂量计算是RPT个体化治疗的重要基础[2-3]。
RPT患者器官水平的吸收剂量可以使用参考体模中源器官每发生一次放射性衰变靶器官的平均吸收剂量(S值)和源器官的累积活度估算[26-27]。这种方法假设器官内的放射性药物和剂量均匀分布,未能考虑患者特异性的活度分布和解剖结构[28]。点核剂量卷积[29]和体素S值[30]等方法能够进行体素级剂量计算,但通常假设人体组织材料密度均匀,忽略了肺组织、软组织和骨之间的差异,剂量计算结果存在误差[30-31]。应用直接MC方法进行体素级剂量计算可以根据CT图像转换得到患者个体化体模的质量密度与材料组成,充分考虑了患者解剖结构的个体化与组织异质性。
本研究ARCHER-NM与GATE在各核素水模体剂量中存在一定差异,主要是由于二者采用的核衰变数据以及对于粒子输运停止的判断逻辑不同。ARCHER-NM核素衰变产物及分支比参考ICRP 107报告[21],并对能谱中产额 < 1×10-4的部分进行了忽略,GATE则使用Geant 4内置的Radioactive Decay库。在粒子输运上,ARCHER-NM中粒子能量一旦低于截止能量则停止输运,能量当地沉积,而GATE则对于初级粒子一律输运至粒子能量为0或从感兴趣区域中逃逸为止,只对次级粒子的生成使用截止射程进行限制。在上述基础上,β核素治疗患者个体化器官剂量中由于药物在体内的特异性分布,较水模体剂量计算使用的点源增加了放射源位置随机采样的误差。不同器官对应的放射源位置以及粒子数量差异较大,且即使ARCHER-NM与GATE均使用患者CT进行异质体模的生成,但在细节上不一定完全一致,也可能引入一定的误差。考虑到MC方法随机性实现方式以及前述粒子输运实现策略的不同,本研究中ARCHER-NM与GATE在水模体剂量与患者剂量计算中差异可以接受。ARCHER-NM应用GPU提高MC算法效率,使完成单例患者剂量计算所需时间大大降低,有利于实现基于剂量的患者个体化核素治疗,进一步提高核素治疗质量控制的精确性。
由于177Lu-DOTATATE等靶向放射性核素治疗药物在我国刚进入临床试验阶段,本研究仅利用密歇根大学数据集所公开的两例患者数据进行了吸收剂量计算及分析,初步验证了ARCHER-NM在靶向放射性核素治疗患者个体化剂量计算中应用的可行性,后续可以通过单中心大数据集上的测试进一步验证其作为临床患者个体化核素治疗剂量计算工具的能力。此外,目前本研究仅对患者器官吸收剂量进行了评估,后续研究可以通过进一步计算生物等效剂量(BED)等指标,进一步量化剂量对病灶和危及器官的影响,以指导患者个体化放射性核素治疗的计划设计。
综上所述,本研究通过核素治疗常用核素点源水模体实验证实了ARCHER-NM剂量计算的正确性以及泛用性;通过两例核素治疗患者个体化剂量计算证实了基于GPU的快速蒙特卡罗计算软件ARCHER-NM能够准确快速的完成核素治疗患者个体化剂量计算。结合自动勾画工具DeepViewer,ARCHER-NM可以实现个体化器官剂量分析,为RPT患者的精准治疗计划提供参考。
利益冲突 无
作者贡献声明 刘君怡负责实验设计实施与论文撰写;程博、彭昭、齐妙协助数据处理和技术指导;裴曦、徐榭负责课题设计和论文修改
| [1] |
Seidlin SM, Marinelli LD, Oshry E. Radioactive iodine therapy: effect on functioning metastases of adenocarcinoma of the thyroid[J]. J Am Med Assoc, 1946, 132(14): 838-847. DOI:10.1001/jama.1946.02870490016004 |
| [2] |
Hardiansyah D, Maass C, Attarwala AA, et al. The role of patient-based treatment planning in peptide receptor radionuclide therapy[J]. Eur J Nucl Med Mol Imaging, 2016, 43(5): 871-880. DOI:10.1007/s00259-015-3248-6 |
| [3] |
Sabet A, Biersack HJ, Ezziddin S. Advances in peptide receptor radionuclide therapy[J]. Semin Nucl Med, 2016, 46(1): 40-46. DOI:10.1053/j.semnuclmed.2015.09.005 |
| [4] |
Neira S, Guiu-Souto J, Díaz-Botana P, et al. Quantification of internal dosimetry in PET patients: individualized Monte Carlo vs generic phantom-based calculations[J]. Med Phys, 2020, 47(9): 4574-4588. DOI:10.1002/mp.14344 |
| [5] |
Zaidi H. Relevance of accurate Monte Carlo modeling in nuclear medical imaging[J]. Med Phys, 1999, 26(4): 574-608. DOI:10.1118/1.598559 |
| [6] |
Zaidi H, Xu XG. Computational anthropomorphic models of the human anatomy: the path to realistic Monte Carlo modeling in radiological sciences[J]. Annu Rev Biomed Eng, 2007, 9: 471-500. DOI:10.1146/annurev.bioeng.9.060906.151934 |
| [7] |
Hissoiny S, Ozell B, Bouchard H, et al. GPUMCD: A new GPU-oriented Monte Carlo dose calculation platform[J]. Med Phys, 2011, 38(2): 754-764. DOI:10.1118/1.3539725 |
| [8] |
Jia X, Gu X, Graves YJ, et al. GPU-based fast Monte Carlo simulation for radiotherapy dose calculation[J]. Phys Med Biol, 2011, 56(22): 7017-7031. DOI:10.1088/0031-9155/56/22/002 |
| [9] |
Jia X, Xu XG, Orton C. Point/counterpoint. GPU technology is the hope for near real-time Monte Carlo dose calculations[J]. Med Phys, 2015, 42(4): 1474-1476. DOI:10.1118/1.4903901 |
| [10] |
Jia X, Ziegenhein P, Jiang SB. GPU-based high-performance computing for radiation therapy[J]. Phys Med Biol, 2014, 59(4): R151-182. DOI:10.1088/0031-9155/59/4/R151 |
| [11] |
Pratx G, Xing L. GPU computing in medical physics: a review[J]. Med Phys, 2011, 38(5): 2685-2697. DOI:10.1118/1.3578605 |
| [12] |
Su L, Yang Y, Bednarz B, et al. ARCHERRT - a GPU-based and photon-electron coupled Monte Carlo dose computing engine for radiation therapy: software development and application to helical tomotherapy[J]. Med Phys, 2014, 41(7): 071709. DOI:10.1118/1.4884229 |
| [13] |
Adam DP, Liu T, Caracappa PF, et al. New capabilities of the Monte Carlo dose engine ARCHER-RT: Clinical validation of the Varian TrueBeam machine for VMAT external beam radiotherapy[J]. Med Phys, 2020, 47(6): 2537-2549. DOI:10.1002/mp.14143 |
| [14] |
Liu T, Lin H, Su L, et al. TU-AB-BRC-10: Modeling of radiotherapy linac source terms using ARCHER Monte Carlo code: performance comparison of GPU and MIC computing accelerators[J]. Med Phys, 2016, 43(6): 3732. DOI:10.1118/1.4957404 |
| [15] |
Xu XG, Liu TY, Su L, et al. ARCHER, a new Monte Carlo software tool for emerging heterogeneous computing environments[J]. Ann Nucl Energy, 2015, 82(0): 2-9. DOI:10.1016/j.anucene.2014.08.062 |
| [16] |
Peng Z, Lu Y, Xu Y, et al. Development of a GPU-accelerated Monte Carlo dose calculation module for nuclear medicine, ARCHER-NM: demonstration for a PET/CT imaging procedure[J]. Phys Med Biol, 2022, 67(6). DOI:10.1088/1361-6560/ac58dd |
| [17] |
Dewaraja YK, Van BJ. Lu-177 DOTATATE anonymized patient datasets[DS]. Univ Michigan(2021). https://deepblue.lib.umich.edu/data/collections/hm50ts030?locale=en.
|
| [18] |
Peng Z, Fang X, Yan P, et al. A method of rapid quantification of patient-specific organ doses for CT using deep-learning-based multi-organ segmentation and GPU-accelerated Monte Carlo dose computing[J]. Med Phys, 2020, 47(6): 2526-2536. DOI:10.1002/mp.14131 |
| [19] |
Wang Z, Chang Y, Peng Z, et al. Evaluation of deep learning-based auto-segmentation algorithms for delineating clinical target volume and organs at risk involving data for 125 cervical cancer patients[J]. J Appl Clin Med Phys, 2020, 21(12): 272-279. DOI:10.1002/acm2.13097 |
| [20] |
Walters BR, Kawrakow I, Rogers DW. History by history statistical estimators in the BEAM code system[J]. Med Phys, 2002, 29(12): 2745-2752. DOI:10.1118/1.1517611 |
| [21] |
Eckerman K, Endo A. ICRP Publication 107. Nuclear decay data for dosimetric calculations[J]. Ann ICRP, 2008, 38(3): 7-96. DOI:10.1016/j.icrp.2008.10.004 |
| [22] |
Ivanchenko V, Apostolakis J, Bagulya A, et al. Recent improvements in Geant4 electromagnetic physics models and interfaces[J]. Prog Nucl Sci Technol, 2011, 2: 898-903. DOI:10.15669/pnst.2.898 |
| [23] |
Daniele P, Lucrezia A, Antonio I, et al. Monte Carlo based dose-rate assessment in 18F-Choline PET examination: a comparison between GATE and GAMOS codes[J]. Atti Accad Peloritana Pericolanti Cl Sci Fis Mat Natur, 2020, 98: 5. |
| [24] |
Chetty IJ, Rosu M, Kessler ML, et al. Reporting and analyzing statistical uncertainties in Monte Carlo-based treatment planning[J]. Int J Radiat Oncol Biol Phys, 2006, 65(4): 1249-1259. DOI:10.1016/j.ijrobp.2006.03.039 |
| [25] |
Low DA, Harms WB, Mutic S, et al. A technique for the quantitative evaluation of dose distributions[J]. Med Phys, 1998, 25(5): 656-661. DOI:10.1118/1.598248 |
| [26] |
Loevinger R, Budinger TF, Watson EE, et al. MIRD primer for absorbed dose calculations(Revised Edition)[M]. Reston, VA: Society of Nuclear Medicine, 1991.
|
| [27] |
Stabin MG, Siegel JA. Physical models and dose factors for use in internal dose assessment[J]. Health Phys, 2003, 85(3): 294-310. DOI:10.1097/00004032-200309000-00006 |
| [28] |
Gupta A, Lee MS, Kim JH, et al. Preclinical voxel-based dosimetry through GATE Monte Carlo simulation using PET/CT imaging of mice[J]. Phys Med Biol, 2019, 64(9): 095007. DOI:10.1088/1361-6560/ab134b |
| [29] |
Giap HB, Macey DJ, Bayouth JE, et al. Validation of a dose-point kernel convolution technique for internal dosimetry[J]. Phys Med Biol, 1995, 40(3): 365-381. DOI:10.1088/0031-9155/40/3/003 |
| [30] |
Amato E, Italiano A, Baldari S. Monte Carlo study of voxel S factor dependence on tissue density and atomic composition[J]. Nucl Instrum Methods Phys Res Sect A: Accel Spectrom Det Assoc Equip, 2013, 729: 870-876. DOI:10.1016/j.nima.2013.08.059 |
| [31] |
Khazaee Moghadam M, Kamali Asl A, Geramifar P, et al. Evaluating the application of tissue-specific dose kernels instead of water dose kernels in internal dosimetry: a Monte Carlo study[J]. Cancer Biother Radiopharm, 2016, 31(10): 367-379. DOI:10.1089/cbr.2016.2117 |
 2024, Vol. 44
2024, Vol. 44
