2. 国家癌症中心 国家肿瘤临床医学研究中心中国医学科学院北京协和医学院肿瘤医院,北京 100021;
3. 中国科学院深圳先进技术研究院,深圳 518055
2. Cancer Hospital, Chinese Academy of Medical Sciences & Peking Union Medical College, National Clinical Research Center for Cancer, National Cancer Center, Beijing 100021, China;
3. Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China
放射治疗是治疗癌症的重要方法,在放疗过程中,胸部和上腹部肿瘤受呼吸运动影响较大,这可能导致肿瘤靶区偏移,同时正常组织受到过多照射。
目前已有一些用来降低呼吸运动影响的方法,如屏气技术和腹部按压技术[1-2]、呼吸门控技术[3]和实时跟踪技术[4]等。屏气和腹部按压技术控制患者呼吸以控制肿瘤运动,不适用于所有患者。呼吸门控技术在呼吸周期的特定阶段照射,可减少呼吸运动导致的误差,但延长了治疗时间。在实时跟踪技术中,系统跟踪肿瘤运动以确保肿瘤始终在治疗范围内,故患者可正常呼吸。但放疗系统的追踪和出束照射存在延迟,如多叶准直器(MLC)[5]延迟约500 ms,射波刀[6]延迟约115 ms,因此,必须预测目标位置以补偿延迟带来的影响。
呼吸运动预测是时间序列预测任务,已有多种机器学习方法应用于此类任务,如人工神经网络(ANN)[7]、递归神经网络(RNN)[8]等。最近,transformer模型[9]被提出,并在时间序列问题下广泛应用。本研究引入一种新的transformer模型——Informer[10],用于预测呼吸运动,最大预测时间约600 ms[11],可适应大多数放疗系统的延迟。本研究将数据集限制在较小的时间尺度,探究训练集长度对预测精度的影响。
资料与方法1. 资料:本研究使用的呼吸运动数据来自乔治敦大学医院射波刀治疗期间采集的公共数据库,由Kevin Cleary博士和Sonja Dieterich博士提供[12]。为了跟踪呼吸运动,每个患者胸部连续放置3个标记物,使用光学跟踪设备记录标记物的位置,采样频率为26 Hz,采样时间25~132 min。该数据库包括31例患者在射波刀治疗过程中记录的运动轨迹,包括每个标记物的三维运动轨迹和对每个标记物的3D运动轨迹进行主成分分析(PCA)后得到的主成分轨迹(一维),共304个运动轨迹。预测算法在PCA处理后的轨迹上的性能给出了对三维轨迹预测性能的合理估计[13]。作为对Informer模型可行性的初步验证,在本研究中,使用PCA处理后的轨迹作为研究对象。在下文中,采用时间步(timestep)作为描述数据长度和时间长度的单位,由于数据的采样频率为26 Hz,故每个时间步的长度为1/26 s(约0.038 5 s)。
2. 数据预处理:本研究中对该数据做了以下预处理:数据截取、数据平滑和数据标准化。使用简单随机抽样选取80条呼吸运动轨迹,并从每条轨迹截取10 min长度,在避开由治疗过程中治疗床的移动造成的突变的前提下[12],截取位置通过简单随机抽样选取。采用Savitzky-Golay滤波器[14]来平滑数据,这是一种基于时域局部多项式最小二乘拟合的滤波方法,广泛用于数据的平滑和去噪。数据标准化是为了提高模型的收敛速度和计算精度,本研究将数据归到均值为0,方差为1的分布中。为了实现输入n个时间步的数据得到Noutput个时间步的预测数据,利用滑动窗口划分每一条呼吸运动轨迹,长度为n+Noutput的窗口沿时间轴方向以一定的步长(通常为1)滑动,每一次滑动获取一条数据,并组合起来得到用于模型训练的数据矩阵。
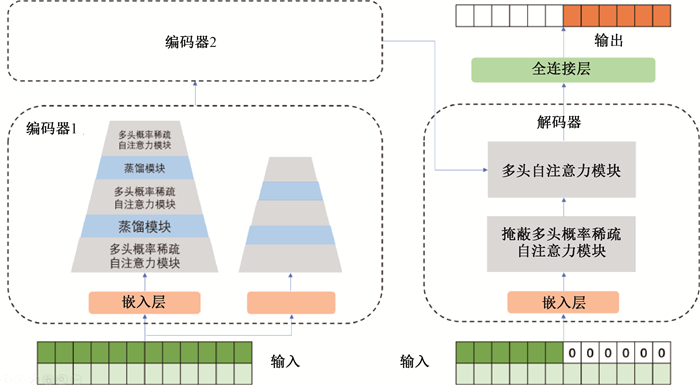
3. 深度学习方法:Informer[10]是一种transformer模型,网络结构如图 1所示,编码器数量Nencoder和解码器数量Ndecoder可按需设置(图示为Nencoder=2,Ndecoder=1)。每个编码器中包括两个堆栈,每个堆栈包括1个输入模块、3个多头概率稀疏(ProbSparse)自注意力模块和2个蒸馏模块。长度为n的序列及时间戳进入输入模块,其中包括1个1×3卷积层和1个嵌入(embeding)层,每个元素的embedding和其时间戳的embedding相加,随后拼接成n×d的矩阵Xen(d为embedding的维度),经过多头概率稀疏自注意力模块(依次为:1个多头概率稀疏自注意力层,1个Add & Norm层,1个前馈网络层,1个Add & Norm层,1个前馈网络层)和蒸馏模块(1个1×3卷积层和1个步长为2的池化层),最终得到n/4×d的输出矩阵;连接两个堆栈的输出作为编码器的输出。解码器为标准的解码器结构,堆叠了两个多头注意力层,不同的是它采用了生成式预测直接输出多步预测结果,而不是通常的逐步(step-by-step)方式,解码器的输入为长度Ntoken+Noutput的序列,即目标序列前长度为Ntoken的序列和目标序列的拼接序列以及时间戳,将目标序列的元素填充为0,经过一个输入模块得到(Ntoken+Noutput)×d的矩阵Xde,依次经过两个多头自注意力模块,其中第二个自注意力模块的K、V矩阵由解码器的输出计算得到,而Q矩阵由第一个多头自注意力模块的输出计算得到,最终得到(Ntoken+Noutput)×d的输出矩阵Z。Z通过一个全连接层得到输出序列,最后的Outputs项即为预测结果,与Target计算loss,loss函数为MSE(mean squared error)。
|
注:编码器2(Encoder 2)与编码器1(Encoder 1)结构相同 图 1 Informer模型结构 Figure 1 Structure of the Informer model |
所有计算都基于以下网络参数设置:Nencoder=2,Ndecoder=1,n=96,Ntoken=1,Noutput=16,epoch = 15,batch size = 16,lr = 0.01,loss = MSE,预测延迟约600 ms。
为了评估Informer网络模型的性能,本研究选择了多层感知器(MLP)[15]和长短期记忆(LSTM)[16]模型作为对比。
MLP是一种基于生物神经元结构得到的神经网络,由多个感知器相互连接而成,单个感知器具有一定的拟合能力,因而多层感知器有更为强大的拟合能力,可以用来解决更复杂的问题。最典型的MLP包括3层:输入层、隐藏层和输出层,不同层之间是全连接的。本研究中使用的MLP模型包括1个96节点的输入层,1个100节点的隐藏层和1个16节点的输出层,epoch = 15,op = Adam,loss = MSE。
LSTM是一种特殊的循环神经网络(RNN),主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题,它通过门控技术来控制传输状态,记住需要长时间记忆的信息,忘记不重要的信息,适用于很多需要长期记忆的任务,但也增加了参数量,导致训练难度加大。LSTM与RNN结构相同,只是将RNN隐藏层中的求和单元用内存块取代。本研究使用的LSTM模型参数为:num_layers = 3,hidden_size = 50,lr = 0.01,epoch = 300,loss = MSE。
4. 评估指标:为了评估实验结果并与其他模型比较,本研究引入归一化均方根误差(nRMSE)和相对均方根误差(rRMSE)[13]作为评估指标,均方根误差(RMSE)和nRMSE分别定义为公式(1)、(2):
| $ \operatorname{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(y_i-\hat{y}_i\right)^2} $ | (1) |
| $ \operatorname{nRMSE}=\frac{\mathrm{RMSE}}{\sigma}=\frac{\sqrt{\frac{1}{N} \sum\nolimits_{i=1}^N\left(y_i-\hat{y}_i\right)^2}}{\sqrt{\frac{1}{N} \sum\nolimits_{i=1}^N\left(\hat{y}_i-\bar{y}_i\right)^2}} $ | (2) |
式中,N为预测轨迹点的数量;yi和
rRMSE定义为:
| $ \begin{gathered} \operatorname{rRMSE}=\frac{\mathrm{RMSE}_{\text {Prediction }}}{\mathrm{RMSE}_{\text {NoPrediction }}}= \\ \frac{\sqrt{\frac{1}{N} \sum\nolimits_{i=1}^N\left(y_i-\hat{y}_i\right)^2}}{\sqrt{\frac{1}{N} \sum\nolimits_{i=1}^N\left(\hat{y}_{i-N_{\text {output }}}-\hat{y}_i\right)^2}} \end{gathered} $ | (3) |
式中,RMSEPrediction和RMSENoPrediction为使用选定的预测方法和无预测方法计算的RMSE值。在无预测方法中,当前轨迹点实际值
对于呼吸运动预测,rRMSE强调了选定的预测方法与无预测方法的性能相比,使用预测方法获得的相对改进。例如,如果rRMSE=0.8,那么可以推断,与系统延迟导致的误差相比,所采用的预测算法能够将误差减少20%。rRMSE值越低,预测方法相对无预测方法提升越大。
5. 统计学处理:采用Excel 2019软件进行数据分析,不同方法的预测结果符合正态分布,组间比较采用配对样本t检验。P < 0.05为差异有统计学意义。
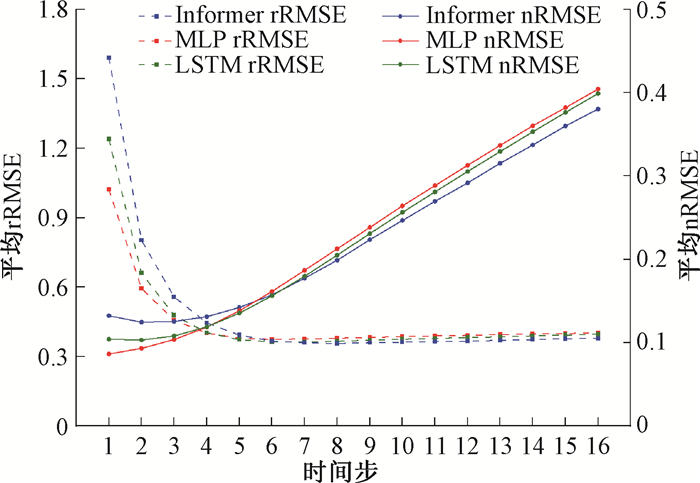
结果1. 模型对比结果:图 2显示的是LSTM、MLP和Informer 3种模型的误差对比。每一条呼吸运动轨迹都被划分为长度比为8∶2的训练集和测试集,各进行10次实验,分别计算预测1~16个时间步(约39~615 ms)的nRMSE和rRMSE平均值。
|
注:实线为归一化均方根误差(nRMSE),虚线为相对均方根误差(rRMSE);MLP. 多层感知器;LSTM. 长短期记忆 图 2 3种模型在1~16个时间步下的预测结果 Figure 2 Prediction results of three models in 1-16 time steps |
预测1~16个时间步的情况下分别对Informer和MLP、Informer和LSTM的预测结果做配对t检验。与MLP模型相比,预测时间步≤4(约154 ms)时,Informer模型的表现差于MLP模型(nRMSE:t=3.99,P < 0.05;rRMSE:t=4.03,P < 0.05);在预测时间步为5、6时,Informer模型和MLP模型的预测结果差异无统计学意义(P>0.05);在预测时间步≥7(约269 ms)时,Informer模型的表现优于MLP模型(nRMSE:t=3.33,P < 0.05;rRMSE:t=2.90,P < 0.05),其中在预测时间步分别为11和16时,nRMSE分别减小6.6%、5.9%(从0.289到0.270、从0.404到0.380),rRMSE分别减小6.4%、6.0%(从0.390到0.365、从0.403到0.379)。与LSTM模型相比,在预测时间步≤5(约192 ms时),Informer表现差于LSTM模型(nRMSE:t=2.62,P < 0.05;rRMSE:t=2.65,P < 0.05);在预测时间步为6、7时,Informer模型和LSTM模型的预测结果差异无统计学意义(P>0.05);在预测时间步≥8 (约308 ms)时,Informer表现优于LSTM模型(nRMSE:t=2.15,P < 0.05;rRMSE:t=1.88,P < 0.05),其中在预测时间步分别为11和16时,nRMSE分别减小3.9%、5.0%(从0.281到0.270、从0.400到0.380),rRMSE分别减小3.7%、4.5%(从0.379到0.365、从0.397到0.379)。这表明Informer模型在预测时间相对较长时有更好的预测效果。
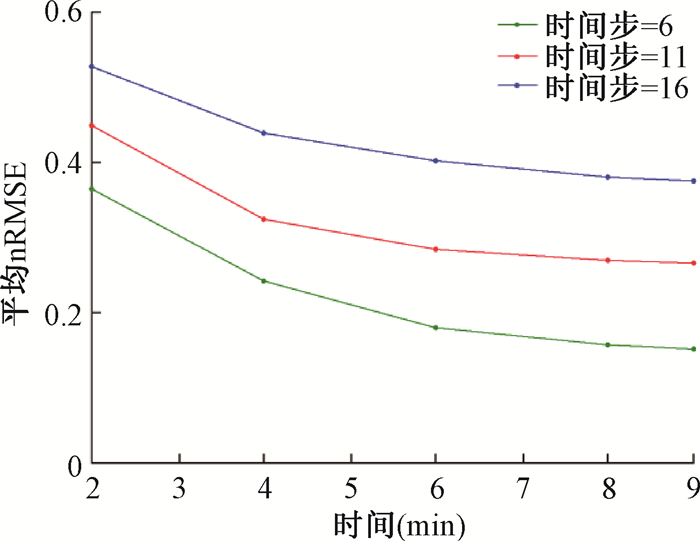
2. 训练集长度对比结果:为了探究训练集长度与预测精度的关系,寻找较合适的训练集长度,本研究分别使用不同训练集长度训练模型,对比它们的预测精度。训练集长度为2、4、6、8、9 min,测试集为运动轨迹中以训练集末尾为起点长度为1 min的部分;每一条轨迹各进行10次实验,分别计算预测时间步为6、11和16(230、423、615 ms)时,预测结果的nRMSE平均值。图 3显示了训练集长度与nRMSE之间的关系,可见随着训练集长度增加,nRMSE逐渐降低,但在训练集长度≥8 min时趋于平缓。因此,在本实验中8 min是一个比较合适的训练集长度。
|
图 3 不同预测时间步、不同训练集长度的预测结果 Figure 3 Predicted results under different prediction time steps and training set lengths |
讨论
本研究引入了Informer用于预测呼吸运动,并比较其与另外两种常用于呼吸运动预测的模型(MLP、LSTM)的性能。另外,本研究也探究了该模型在不同训练集长度下的性能差异,以确定较为合适的训练集长度。结果显示,Informer在较长的预测时间上有一定优势。在数据集长度为10 min的情况下,训练集长度≥8 min时可以取得较好的预测效果。
由于不同数据的幅度不同、同一数据不同位置的幅度不同,采用使用相对单位的评估指标可以较好地对比不同数据以及同一数据的不同划分方式下的预测结果,如本研究采用的nRMSE和rRMSE。此外,在对预测结果的分析中发现,随着测试集长度的增加,预测的总体准确度会降低,推测这是由于时间序列上通常距离越远的点相关性越差,距离训练集更远处包含了更多训练集中没有的特征所导致,因此在对比不同训练集长度的预测效果时,为了尽可能保证对比的公平性,对比了以训练集末尾为起点、相同时间长度的预测结果,而不是直接对比测试集结果(数据总长不变,不同训练集长度对应了不同的测试集长度),这里对比了1 min长度的预测结果。由于本研究使用的数据集长度为10 min,在对比不同训练集长度下预测性能的研究中,最大训练集长度设定为9 min。
本研究的局限性包括:采取的训练方式为对单个呼吸运动数据的离线训练,难以应对呼吸模式的变化,如果需要应对呼吸模式的变化,可能需要采用在线训练的方式,即在预测效果下降至不可接受之前,利用新获得的呼吸运动数据更新模型,将在未来的研究中对此做进一步探讨;此外,本研究预测体外标记物的运动轨迹,需要建立体外标记物与体内肿瘤运动的相关模型,目前已有的相关模型仍有一些问题需要解决。
利益冲突 无
作者贡献声明 晋國棟负责实施研究、数据处理和论文撰写;刘宇翔负责指导研究、数据收集和分析;杨碧凝、魏然负责指导研究;陈辛元、梁晓坤、全红和戴建荣负责论文审阅;门阔负责课题设计、指导研究和论文修改
| [1] |
Wong JW, Sharpe MB, Jaffray DA, et al. The use of active breathing control (ABC) to reduce margin for breathing motion[J]. Int J Radiat Oncol Biol Phys, 1999, 44(4): 911-919. DOI:10.1016/s0360-3016(99)00056-5 |
| [2] |
Herfarth KK, Debus J, Lohr F, et al. Extracranial stereotactic radiation therapy: set-up accuracy of patients treated for liver metastases[J]. Int J Radiat Oncol Biol Phys, 2000, 46(2): 329-335. DOI:10.1016/s0360-3016(99)00413-7 |
| [3] |
Lu HM, Brett R, Sharp G, et al. A respiratory-gated treatment system for proton therapy[J]. Med Phys, 2007, 34(8): 3273-3278. DOI:10.1118/1.2756602 |
| [4] |
Murphy MJ. Tracking moving organs in real time[J]. Semin Radiat Oncol, 2004, 14(1): 91-100. DOI:10.1053/j.semradonc.2003.10.005 |
| [5] |
Krauss A, Nill S, Tacke M, et al. Electromagnetic real-time tumor position monitoring and dynamic multileaf collimator tracking using a Siemens 160 MLC: geometric and dosimetric accuracy of an integrated system[J]. Int J Radiat Oncol Biol Phys, 2011, 79(2): 579-587. DOI:10.1016/j.ijrobp.2010.03.043 |
| [6] |
Kilby W, Dooley JR, Kuduvalli G, et al. The CyberKnife robotic radiosurgery system in 2010[J]. Technol Cancer Res Treat, 2010, 9(5): 433-452. DOI:10.1177/153303461000900502 |
| [7] |
Seregni M, Pella A, Riboldi M, et al. Real-time tumor tracking with an artificial neural networks-based method: a feasibility study[J]. Phys Med, 2013, 29(1): 48-59. DOI:10.1016/j.ejmp.2011.11.005 |
| [8] |
Elman JL. Finding structure in time[J]. Cogn Sci, 1990, 14(2): 179-211. DOI:10.1207/s15516709cog1402_1 |
| [9] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]. Long Beach California: Conference on Neural Information Processing Systems, 2017. DOI: 10.48550/arXiv.1706.03762.
|
| [10] |
Zhou H, Zhang S, Peng J, et al. Informer: Beyond efficient transformer for long sequence time-series forecasting[C]. On line: AAAI Conference on Artificial Intelligence, 2021.
|
| [11] |
Tan M, Peng H, Liang X, et al. LSTformer: long short-term transformer for real time respiratory prediction[J]. IEEE J Biomed Health Inform, 2022, 26(10): 5247-5257. DOI:10.1109/JBHI.2022.3191978 |
| [12] |
Ernst F. Compensating for Quasi-periodic motion in robotic radiosurgery[M]. New York: Springer, 2012.
|
| [13] |
Wang YB, Yu ZB, Sivanagaraja T, et al. Fast and accurate online sequential learning of respiratory motion with random convolution nodes for radiotherapy applications[J]. Appl Soft Comput, 2020, 95(1): 106528. DOI:10.1016/j.asoc.2020.106528 |
| [14] |
Savitzky A, Golay MJ. Smoothing and differentiation of data by simplified least squares procedures[J]. Anal Chem, 1964, 36(8): 1627-1639. DOI:10.1021/ac60214a047 |
| [15] |
Rumelhart DE, Hinton G, Williams RJ. Learning repre-sentations by back-propagating errors[J]. Nature, 1986, 323(6088): 533-536. |
| [16] |
Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Comput, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
 2023, Vol. 43
2023, Vol. 43


