2. 中北大学软件学院,太原 030051;
3. 中北大学信息与通信工程学院,太原 030051;
4. 山西省肿瘤医院放射治疗科,太原 030013
2. School of Software, North University of China, Taiyuan 030051, China;
3. School of Information and Communication Engineering, North University of China, Taiyuan 030051, China;
4. Department of Radiation Oncology, Shanxi Provincial Cancer Hospital, Taiyuan 030013, China
研究表明,低剂量的辐射会造成一定的生物损伤[1-3]。DNA损伤所致基因突变是辐射致癌的主要原因[4-5],因此,研究DNA辐射损伤对癌症预防和治疗有重要意义。蒙特卡罗径迹结构法是研究DNA损伤最主要的模拟方法。Franken等[6]在γ-H2AX焦点实验中发现,高传能线密度(linear energy transfer,LET)电离辐射后的双链断裂(double strand break, DSB)产额表示的相对生物效能(relative biological effectiveness,RBE)值,与染色体片段、细胞存活信息表示的RBE值没有关联性。Francis等[7]、Meylan等[8]、Lampe等[9-10]和de la Fuente Rosales等[11]模拟计算出辐射生成的DNA单链断裂(single strand break,SSB)和DSB产额值,但没有提供集簇性DNA损伤的信息。集簇性DNA损伤中DSB损伤簇是最具破坏性的病变之一,且难以修复[12-15]。Montgomery等[16]提出了用中子直接诱导的DNA集簇性损伤评估RBE的新方法,验证了DSB损伤簇提高粒子随机效应RBE,且与粒子能量相关的假设。但该研究只是从物理过程模拟了中子的损伤过程,忽略了生物化学过程。
本研究通过追溯基本的生物物理原理,基于放射生物学蒙特卡罗模拟软件Geant4-DNA(法国国家核物理与粒子物理研究所,IN2P3),在已有研究基础上[17-18],以低能电子、质子和α粒子为主要的研究对象,对这些粒子辐射后产生的DNA损伤设计一种新的RBE评估方法,以验证该方法同染色体畸变、生殖细胞死亡相似的生物效应。在基于损伤点密度的含噪声密度聚类(density-based spatial clustering of applications with noise, DBSCAN)算法的基础上,改进DSB损伤簇分类方法,以减弱模拟过程中损伤点与能量沉积均匀性随机分布假设的联系,使得DSB损伤簇分布更接近于非随机性。重点研究相近LET值的质子和α粒子,从DNA损伤机制的物理过程和化学过程分析DSB损伤簇分布差异。本研究包含多个损伤的DSB损伤簇复杂度和数量,同时评估了Geant4-DNA中表征电离辐射相互作用的不同物理模型和化学参数的差别。
材料与方法1. 物理作用及Geant4-DNA的物理模型:电离辐射发生后,放射性粒子以3种方式与生物大分子发生相互作用:分别是非弹性碰撞、弹性碰撞和核反应。这些物理作用产生大量的电离辐射能量沉积点,使得DNA分子被电离粒子直接击中,发生链断裂。Geant4-DNA蒙特卡罗开源平台提供了一套完整的逐步(step-by-step)描述不同粒子与液态水媒质发生电离物理反应的模型集[19]。目前,Geant4-DNA用于模拟低能电子与液态水媒质中粒子的相互作用的构造函数有5个:G4EmDNAPhysics、G4EmDNAPhysics_option2、G4EmDNAPhysics_option4、G4EmDNAPhysics_option6和G4EmDNAPhysics_option8,分别缩写为POpt0、POpt2、POpt4、POpt6和POpt8,电子、质子、α粒子Geant4-DNA物理模型如表 1~3所示。
|
|
表 1 电子Geant4-DNA物理模型 Table 1 Physical model of Geant4-DNA for electrons |
|
|
表 2 质子Geant4-DNA的物理模型 Table 2 Physical model of Geant4-DNA for protons |
|
|
表 3 α粒子Geant4-DNA的物理模型 Table 3 Physical model of Geant4-DNA for α particles |
2. 化学作用及Geant4-DNA的化学模型:电离辐射作用于生物机体后,水解离产物羟自由基(·OH)攻击DNA分子诱发了DNA的间接损伤[20]。Geant4-DNA的化学模型通过3个连续阶段描述电离辐射在液态水媒质的作用:第1阶段经过物理模型,计算低能电子与液态水的非弹性反应截面、弹性反应截面等物理过程;第2阶段沉积了能量的水分子发生电离和激发;第3阶段水分子的辐解产物发生布朗扩散和化学反应。目前,Geant4-DNA用于模拟化学过程的构造函数有4个:G4EmDNAChemistry、G4EmDNAChemistry_option1、G4EmDNAChemistry_option2、G4EmDNAChemistry_option3,分别缩写为COpt0、COpt1、COpt2和COpt3,模型中发生变化的参数包括:化学阶段中各扩散反应物的扩散系数见表 4[18-19],化学反应及反应率常数K见表 5[18-19]。
|
|
表 4 化学阶段中各扩散反应物的扩散系数D(10-9·m2·s-1)[18-19] Table 4 Diffusion coefficients of the diffusing species in chemical process (10-9·m2·s-1)[18-19] |
3. 模拟:前期基于损伤概率密度函数的简化几何模型的研究,实现了加速模拟且不损失模拟精度的目的[17-18]。构建轴半径依次为9.85、7.1、2.5 μm的椭圆球状的成纤维细胞核的几何优化模型。在Geant4-DNA(软件版本Geant4.10.07)平台上模拟质子,α粒子照射成纤维细胞核的过程,计算多种DSB损伤簇产额,并参考γ射线计算RBE值。
4. 集簇性损伤算法:原有基于DBSCAN算法的DNA链断裂分类[17-18]方法中,将ε邻域内超过5个损伤点的簇都聚集到1个链断裂分类中,使得各类DSB损伤簇产生的相对频率均低于Nikjoo等[21]的结果。因此,本研究将DSB损伤簇,即原来DSB损伤点个数≥5且不考虑损伤点间隔距离的损伤簇的分类进一步细化,见表 6。此方法的依据有三点:①DBSCAN算法的邻域参数(ε,m)[17],距离阈值ε和点数m分别代表了可以形成损伤簇的相邻点间的最大距离和形成DSB损伤簇的最小SSB数量,它们的取值分别是3.2 nm和2个,因此,DSB损伤簇分类中,已经排除了SSB的存在。②DBSCAN算法包含了DNA链损伤发生位置的判断,细化分类的DSB损伤簇不包含SSB+。③分类过程中,优先考虑较低复杂度的损伤簇基本类型,即按照DSB、DSB+、DSB++的优先级依次组合。参考Friedland等[22]将1% SSB直接转化为DSB的方法,并考虑到简化模型无法模拟DNA的扭曲几何状态,低估DSB的产额,因此,本研究将5% SSB直接转化为DSB。
|
|
表 6 DNA链断裂的分类方法 Table 6 Classification of DNA strand breaks |
5. 表征参数LET的计算:质子、α粒子等辐射具有较高的依赖于能量的相对生物效能。作为表征参数,与能量相关的LET的计算对结果有着重要的影响。LET与衡量电离密度的指标——电离比度成正比。单位长度径迹上形成的离子数越多,LET值就越高。质子和α粒子放射产生的能量沉积点密集,被称为高LET辐射。
电离粒子LET的计算与其碰撞阻止本领(stopping power,SP)计算方法相近,前者由单位长度径迹上沉积的能量来计算,后者由粒子的能量损失来定义,在国际辐射单位和测量委员会(International Commission on Radiation Units and Measurements,ICRU)90号[23]报告中,通过LETΔ = SPel -(dEke, Δ / dl)表达了LET与SP的关系。式中,Δ是能量转移的限定值;SPel是电离反应的SP;dEke, Δ / dl是粒子电离产生的次级电子(>Δ能量值)移动dl距离后剩余动能均值。如果没有能量限定值,则LET = SPel。因此,LET的计算结果可参照ICRU报告的SP值[23]做对比。
6. DSB损伤簇产额及产生的相对频率:计算DSB损伤簇产额如公式(1)所示:
| $ Y_{\mathrm{DSBC}}=\frac{N_{\mathrm{DSBC}}}{D_{N_{\mathrm{DSBC}}} \times N_{\mathrm{bp}}} $ | (1) |
式中,NDSBC为DSB损伤簇的总个数;DNDSBC为粒子在细胞核内的吸收剂量,Gy;Nbp为细胞核内碱基对(base pair, bp),6×109 bp;YDSBC为产额,Gy-1 ·bp-1 ·10-9。
模拟结果的精度需以分子生物学实验结果为参考来验证。从Vyšín等[24]的结论可以看出,即使在相同LET下,实验产生的DSB链断裂产额也会不同,因为不同剂量、质粒几何结构的差异等都给实验结果带来不确定性。Vyšín等[24]和Garty等[25]的实验对象都是质粒DNA,本研究模拟的是成纤维细胞核,要衡量不同实验的DNA损伤结果,本研究采用了DSB损伤簇产生的相对频率评估,即不同的DSB损伤簇占所有DNA链断裂的比例,如公式(2)所示,以呈现良好的对比效果。
| $ F=\frac{Y_{\mathrm{DSBC}}}{Y_{\mathrm{SB}}} \times 100 \% $ | (2) |
7. RBE:RBE指产生相同生物效应时,参考射线所需剂量与该种射线所需剂量的比值。为评估低剂量下粒子的RBE,本研究给出了质子(p)、α粒子诱导的各DSB损伤簇剂量以γ射线作为参考射线的RBE计算公式,如公式(3)所示。式中字母含义与公式(1)相同。此时的相同生物效能即生成相同数量的DSB损伤簇的吸收剂量之比,由公式(1)可得,RBE值等同于质子、α粒子诱导的各DSB损伤簇产额与γ射线产额的比值。
| $ \mathrm{RBE}_{\mathrm{DSBC}}=\frac{D_{N_{\mathrm{DSBC}}} \mid \gamma}{D_{N_{\mathrm{DSBC}}} \mid \alpha \text { 或 } \mathrm{p}}=\frac{Y_{\mathrm{DSBC}} \mid \alpha \text { 或 } \mathrm{p}}{Y_{\mathrm{DSBC}} \mid \gamma} $ | (3) |
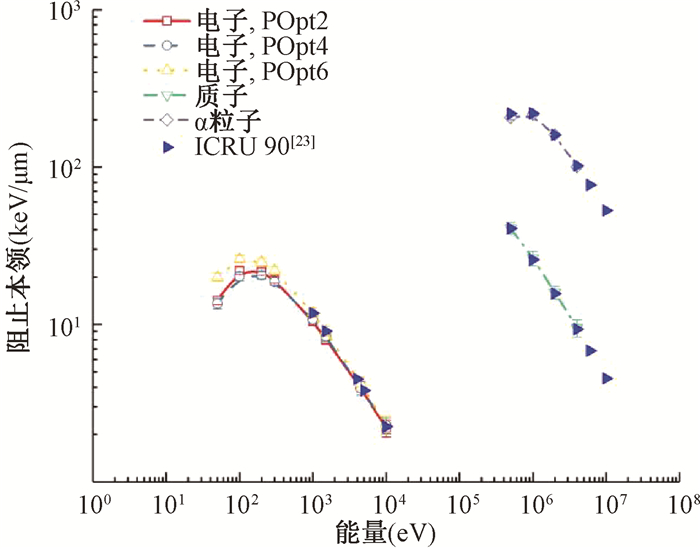
1. 物理模型对LET计算的影响:SP的结果差异表明了物理模型的影响,也反映了LET值因为不同构造函数的计算差异。在POpt2、POpt4、POpt6不同的设置下,质子和α粒子物理模型一致,不考虑次级电子的传输。因此,质子和α粒子的SP计算结果一致。低能电子的SP则受物理模型影响较大,如图 1所示,低能电子的SP计算结果中,POpt2和POpt4相近;POpt2和POpt6差异较大。这是因为低能电子的SP根据不同非弹性物理模型的横截面分析计算获得,POpt2和POpt4具有相近的非弹性物理模型,POpt6的CPA100电离截面积要略高于另外两个模型,大约在1%以内[26]。如图 1所示,POpt6模型下1~5 keV的电子与ICRU 90[23]最接近,相差不到1%。因此,POpt6的电离模型是在水媒质模拟结果最接近实验数据的。
|
图 1 液态水中电子、质子和α粒子的阻止本领与入射能量的关系 Figure 1 Relationship between the stopping power of electrons, protons, and α particles and the incident energy in liquid water |
如表 7所示,采用POpt2物理模型,通过模拟质子和α粒子穿过1 μm厚度水薄片的能量沉积方法,计算得到的LET均值与ICRU 90[23]的SP值相比较。次级电子能量转移的限定值Δ由POpt2模型中电子能量域的最小值7.4 eV决定。对于质子,计算的LET值与ICRU 90[23]的全阻止本领误差值在2%以内。对于α粒子,LET值与ICRU 90[23]的值误差较大。
|
|
表 7 质子和α粒子的阻止本领与计算所得LET均值的比较 Table 7 Comparison of the stopping power and the calculated average LET of protons and α particles |
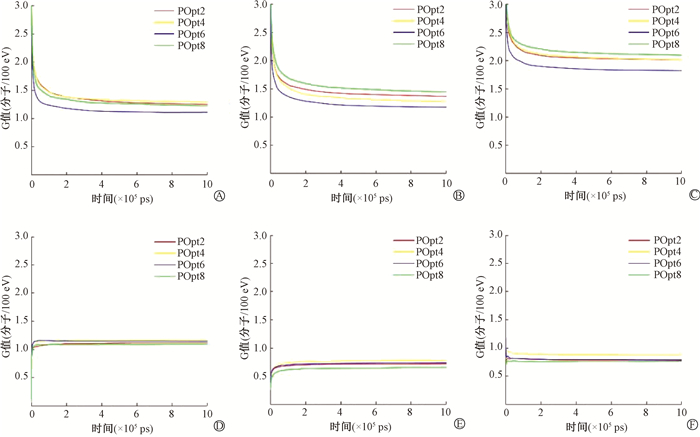
2. 物理模型对化学过程中水解离生成物产额的影响:POpt2、POpt4和POpt6、POpt8的弹性散射模型对比中,前两者散射更分散,后两者散射更集中。它们不会直接导致能量上的损失,因此对SP的计算影响不大。但物理弹性反应决定了电离的分布,诱导的水解离反应程度不同。即化学参数统一的情况下,虽然所有的模型产生相同数量的水解离产物,但是化学反应的模拟是依据水解离产物之间的距离来确定是否发生反应,因此,分散的Champion等[27-28]分波模型和Uehara屏蔽卢瑟福模型发生的化学反应少,CPA100模型生成更多的化学反应。CPA100模型中,解离过程中生成的·OH、eaq-和H3O+等因为相互反应而消失的更多,如图 2所示,采用CPA100弹性散射模型的POpt6生成的这3个水解物辐射化学产额(G-value,G值)最小,它们与DNA间接损伤的产额有着直接的关系。
|
图 2 不同物理模型下·OH(A)、eaq-(B)、H3O+(C)、H2O2(D)、H2(E)和H·(F)的G值图 Figure 2 G-value diagrams of ·OH(A), eaq-(B), H3O+(C), H2O2(D), H2(E)and H·(F) according to different physical models |
3. 不同物理模型的SSB和DSB相对剂量对比:如图 3所示,当使用不同的物理构造函数进行模拟时,SSB和DSB对总DSB的贡献也不同。图上产额差异比值以POpt8的数据为基准,POpt2和POpt6得出的DNA链断裂产额与之相比较。差异比值正值代表高出POpt8数据的比率;负值代表低于POpt8数据的比率。对比图验证了:当非弹性物理模型一致的时候,POpt2比POpt8更分散的弹性散射决定了电离簇和·OH更分散的空间分布,使得前者的SSB产额高于后者,而DSB产额则是汇聚性更强的CPA100模型生成的更多;当弹性物理模型一致的时候,POpt6比POpt8的非弹性模型高出1%的电离截面积,POpt6较高的电离密度增加了局部区域电离簇的密度,DSB产额增加,SSB产额减少。

|
图 3 不同物理构造函数的SSB(A)和DSB(B)产额差异比值 Figure 3 The difference yields of SSB(A)and DSB(B)based on different physical constructors |
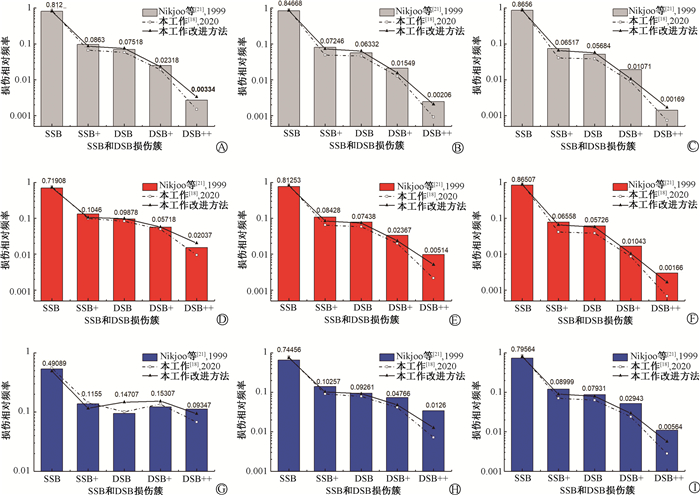
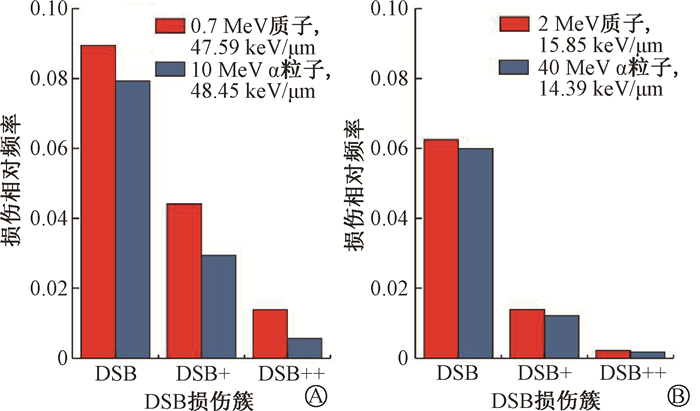
4. 复杂DSB损伤簇的比较:高LET粒子辐射下,DNA碎片的分布不是随机的,能产生更复杂的损伤。如图 4所示,研究中不同类型的DSB损伤簇的相对频率分布趋势和Nikjoo等[21]的结果相同。本研究中,对DSB损伤簇的产额计算进行了新的分类方法,结果相较于之前的研究[18]更接近于Nikjoo等[21]的研究结果。对于LET相近的质子和α粒子,如图 5所示,质子的复杂DSB损伤簇的相对频率更高。
|
图 4 不同类型DNA集簇性损伤的相对频率分布 A.电子0.3 keV;B.电子1.5 keV;C.电子4.5 keV;D.质子0.5 MeV;E.质子1 MeV;F.质子4 MeV;G.α粒子2 MeV;H.α粒子6 MeV;I.α粒子10 MeV Figure 4 Relative frequency distribution of different types of DNA clusters A. 0.3 keV electron; B. 1.5 keV electron; C. 4.5 keV electron; D. 0.5 MeV proton; E. 1 MeV proton; F. 4 MeV proton; G. 2 MeV α-particle; H. 6 MeV α-particle; I. 10 MeV α-particle |
|
图 5 相近LET质子和α粒子DSB损伤簇的相对频率分布 A. 0.7 MeV质子和10 MeV α粒子;B. 2 MeV质子和40 MeV α粒子 Figure 5 Relative frequency distributions of DSB clusters of the same LET protons and α-particles A. 0.7 MeV proton and 10 MeV α-particle; B. 2 MeV proton and 40 MeV α-particle |
5. 复杂DSB损伤簇的RBE:如表 8所示(表中LET是在细胞核环境中计算[18]),DSB剂量仅表示单一DSB,即不包含DSB损伤簇,RBEDSB只针对单一DSB计算。γ射线DSB产额采用Belli等[29]碎片计数法的值。表中质子和α粒子产生的DSB产额要比γ射线分别高出1.57和2.11倍。这一结果与Belli等[29]的碎片计数法相同范围内质子(1.9±0.1)和α粒子(1.2±0.1)的RBE值相近。相应地,以DSB损伤簇计算的RBEDSBC普遍高于RBEDSB值。2 MeV α粒子的RBEDSBC(12.29)与Franken等[6]表 1中呈现的以染色体片段(15.3±5.9)、细胞存活RBE(14.7±5.1)相近,而此时的RBEDSB只有2.07。
|
|
表 8 质子和α粒子的DSB、DSB损伤簇及其RBE值 Table 8 DSB, DSB clusters and RBEs of protons and α particles |
表 8中DSB+和DSB++损伤簇占DSB的比值体现了不同粒子RBE的能量相关性。同时也给出了相近LET的质子和α粒子,有着不同的RBEDSB和RBEDSBC值。质子的RBE值和DSB损伤簇的比值都高于同等LET的α粒子。这是因为它们都和能量沉积状态和能量转移位置相关,因此质子拥有更高的RBE。
讨论电离辐射导致DNA损伤的物理化学模型直接影响了DNA链断裂产额的计算。本研究通过模拟不同能量、不同类型的粒子在成纤维细胞核几何模型上的辐照过程,实现蒙特卡罗径迹结构方法中不同物理模型和化学参数对计算DNA链断裂产额影响的评估。
Geant4-DNA 5种构造函数使用相同的质子和α粒子物理模型。质子和α粒子的SP计算结果一致。计算LET过程中,由于模拟粒子穿过的1 μm厚度水薄片足够薄,入射质子能量基本很少变化,而且这个过程质子不发生偏转,也确实保证了有足够数量的相互作用来决定能量损失,因此,质子的LET值与ICRU 90[23]的全阻止本领误差值较小。对于α粒子,LET值与ICRU 90[23]的值误差较大。因为计算过程不能忽略α粒子侧向偏转造成的动能损失,在Tran等[30]给出了弹性散射过程中的粒子能量损失公式,如式(4)所示:
| $ \Delta E=W(\theta, T)=4 T \frac{m_p M_t}{\left(m_p+M_t\right)^2} \sin ^2\left(\frac{\theta}{2}\right) $ | (4) |
式中,mp和 Mt分别为放射粒子和其撞击对象的质量;θ为侧向散射偏转角度。散射角的分布取决于物理模型中的微分截面。粒子的初始能量越大,传递给次级电子能量越大,α粒子其产生的次级电子远远多于质子[31]。因此,计算LET过程中,需要扣除次级电子移动后剩余动能均值。由此α粒子的LET值小于SP值,且能量越大,差异率也越大。
对于LET相近的质子和α粒子,质子的复杂DSB损伤簇的相对频率更高。这是因为α粒子传递给次级电子的动能要高于相近LET的质子,能量高的电子相互作用截面较低,因此这些电子具有较高的平均自由程,从而导致了较为稀疏的能量沉积。这也就解释了质子的能量通过低能电子传递,能量转移保持在质子轨道附近,使得DSB损伤簇的空间集中度相对较高的原因。
本研究改进后的DSB损伤簇分类方法细化了复杂损伤簇的分类,减弱了损伤簇概率分布随机产生的均匀性,使得DSB损伤簇更接近于非随机分布。随着DSB损伤簇中损伤点数的递增,DSB损伤簇产生的频率不断上升。表 8中DSB+和DSB++ 占DSB损伤总数的比值表明,非随机分布的DSB损伤簇产额在计算机模拟中,占据着一定的DNA链断裂比例。而在生物实验中,代表了DSB损伤簇的小尺寸碎片经常被忽略,不计入DSB产额。但小碎片更容易导致细胞的失活和突变。因此,作为以细胞失活和突变为生物终点的参考性RBE研究,仅以简单DSB的产额计算,是无法建立细胞水平上所产生的生物水平与DSB产额的联系。而DSB损伤簇有着与染色体片段、细胞存活信息相关的高LET辐射的生物有效性相关的信息。但本研究可参考的细胞生物学实验结果极少,这一结论仍需要更多的生物学实验数据验证,且Geant4-DNA目前可模拟的粒子模型也有限,无法实现其他粒子如重离子在纳米级原子几何模型上的模拟。
综上,本研究以低能电子、质子和α粒子为主要的研究对象,通过计算机模拟粒子辐照过程。不同的物理模型不仅影响直接过程中的损伤结果,也影响了化学过程中水解离产物的产额,从而间接地影响DNA链断裂产额。质子和α粒子几个构造模型中电离散射模型一致,但生成的次级电子能量沉积状态和能量转移位置差异决定了SSB和DSB产额差异。本研究提出的一种新的DSB损伤簇分类方法,使得前期的基于损伤概率密度函数的简化几何模型计算更准确,各类DSB损伤簇产额精度更接近于细胞具体几何模型的模拟结果。由非随机分布的DSB损伤簇产额计算的RBE值能体现出与实验中染色体片段、细胞存活信息的生物效应的关联性。因此,通过计算机模拟低剂量质子、α粒子的辐射过程,从生物物理原理来获取DSB损伤簇的RBE值,成为评估电离辐射随机效应评估的一种手段。
利益冲突 所有研究者均未因进行该研究而接受任何不正当的职务或财务利益,在此对研究的独立性和科学性予以保证
作者贡献声明 唐菁负责实验设计及操作、数据处理和论文撰写;马骥祥负责数据采集和起草论文;李志媛负责数据采集和统计分析;李杰负责医学技术和论文思路指导;张鹏程指导论文修改
| [1] |
Garzillo C, Pugliese M, Loffredo F, et al. Indoor radon exposure and lung cancer risk: a meta-analysis of case-control studies[J]. Transl Cancer Res, 2017, 6(S5): 1-10. DOI:10.21037/tcr.2017.05.42 |
| [2] |
贾向红, 许峰, 白延强, 等. 银河宇宙射线对登月航天员辐射危险分析[J]. 航天医学与医学工程, 2013, 26(5): 410-415. Jia XH, Xu F, Bai YQ, et al. Risk analysis of galactic cosmic radiation on astronauts to moon[J]. Space Med Med Eng, 2013, 26(5): 410-415. |
| [3] |
Tawn EJ, Curwen GB, Jonas P, et al. Chromosome aberrations determined by sFISH and G-banding in lymphocytes from workers with internal deposits of plutonium[J]. Int J Radiat Biol, 2016, 92(6): 312-320. DOI:10.3109/09553002.2016.1152414 |
| [4] |
Vaux DL. In defense of the somatic mutation theory of cancer[J]. Bioessays, 2011, 33(5): 341-343. DOI:10.1002/bies.201100022 |
| [5] |
Rashid S. Cancer and chemoprevention: an overview[M]. Berlin: Springer, 2017: 3-13. DOI:10.1007/978-981-10-2579-2_2
|
| [6] |
Franken NA, Hovingh S, Ten Cate R, et al. Relative biological effectiveness of high linear energy transfer α-particles for the induction of DNA-double-strand breaks, chromosome aberrations and reproductive cell death in SW-1573 lung tumour cells[J]. Oncol Rep, 2012, 27(3): 769-774. DOI:10.3892/or.2011.1604 |
| [7] |
Francis Z, Villagrasa C, Clairand I. Simulation of DNA damage clustering after proton irradiation using an adapted DBSCAN algorithm[J]. Comput Methods Programs Biomed, 2011, 101(3): 265-270. DOI:10.1016/j.cmpb.2010.12.012 |
| [8] |
Meylan S, Incerti S, Karamitros M, et al. Simulation of early DNA damage after the irradiation of a fibroblast cell nucleus using Geant4-DNA[J]. Sci Rep, 2017, 7(1): 11923. DOI:10.1038/s41598-017-11851-4 |
| [9] |
Lampe N, Karamitros M, Breton V, et al. Mechanistic DNA damage simulations in Geant4-DNA part 1: a parameter study in a simplified geometry[J]. Phys Med, 2018, 48: 135-145. DOI:10.1016/j.ejmp.2018.02.011 |
| [10] |
Lampe N, Karamitros M, Breton V, et al. Mechanistic DNA damage simulations in Geant4-DNA Part 2: electron and proton damage in a bacterial cell[J]. Phys Med, 2018, 48: 146-155. DOI:10.1016/j.ejmp.2017.12.008 |
| [11] |
de la Fuente Rosales L, Incerti S, Francis Z, et al. Accounting for radiation-induced indirect damage on DNA with the Geant 4-DNA code[J]. Phys Med, 2018, 51: 108-116. DOI:10.1016/j.ejmp.2018.06.006 |
| [12] |
Gulston M, Fulford J, Jenner T, et al. Clustered DNA damage induced by gamma radiation in human fibroblasts (HF19), hamster (V79-4) cells and plasmid DNA is revealed as Fpg and Nth sensitive sites[J]. Nucleic Acids Res, 2002, 30(15): 3464-3472. DOI:10.1093/nar/gkf467 |
| [13] |
David-Cordonnier MH, Cunniffe SMT, Hickson ID, et al. Efficiency of incision of an AP site within clustered DNA damage by the major human AP endonuclease[J]. Biochem J, 2002, 41: 634-642. DOI:10.1021/bi011682l |
| [14] |
Lomax ME, Cunniffe S, O'Neill P. 8-OxoG retards the activity of the ligase Ⅲ/XRCC1 complex during the repair of a single-strand break, when present within a clustered DNA damage site[J]. DNA Repair (Amst), 2004, 3(3): 289-299. DOI:10.1016/j.dnarep.2003.11.006 |
| [15] |
Eot-Houllier G, Eon-Marchais S, Gasparutto D, et al. Processing of a complex multiply damaged DNA site by human cell extracts and purified repair proteins[J]. Nucleic Acids Res, 2005, 33(1): 260-271. DOI:10.1093/nar/gki165 |
| [16] |
Montgomery L, Lund CM, Landry A, et al. Towards the characterization of neutron carcinogenesis through direct action simulations of clustered DNA damage[J]. Phys Med Biol, 2021, 66(20): 205011. DOI:10.1088/1361-6560/ac2998 |
| [17] |
唐菁, 张鹏程, 肖钦峰, 等. 基于含噪声密度聚类算法的质子辐射诱导的DNA集簇性损伤研究[J]. 生物医学工程学杂志, 2019, 4: 633-642. Tang J, Zhang PC, Xiao QF, et al. Study of clustered damage in DNA after proton irradiation based on density-based spatial clustering of applications with noise algorithm[J]. J Biomed Eng, 2019, 4: 633-642. DOI:10.7507/1001-5515.201812008 |
| [18] |
Tang J, Xiao QF, Gui ZG, et al. Simulation of proton-induced DNA damage patterns using an improved clustering algorithm[J]. Radiat Res, 2020, 194(4): 363-378. DOI:10.1667/RR15552.1 |
| [19] |
Bernal MA, Bordage MC, Brown J, et al. Track structure modeling in liquid water: a review of the Geant4-DNA very low energy extension of the Geant4 Monte Carlo simulation toolkit[J]. Phys Med, 2015, 31(8): 861-874. DOI:10.1016/j.ejmp.2015.10.087 |
| [20] |
Leloup C, Garty G, Assaf G, et al. Evaluation of lesion clustering in irradiated plasmid DNA[J]. Int J Radiat Biol, 2005, 81(1): 41-54. DOI:10.1080/09553000400017895 |
| [21] |
Nikjoo H, O'Neill P, Wilson WE, et al. Computational approach for determining the spectrum of DNA damage induced by ionizing radiation[J]. Radiat Res, 2001, 156(5 Pt 2): 577-583. DOI:10.1667/0033-7587(2001)156[0577:cafdts]2.0.co;2 |
| [22] |
Friedland W, Schmitt E, Kundrát P, et al. Comprehensive track-structure based evaluation of DNA damage by light ions from radiotherapy-relevant energies down to stopping[J]. Sci Rep, 2017, 7: 45161. DOI:10.1038/srep45161 |
| [23] |
Seltzer SM, Fernandez-Varea JM, Andreo P, et al. ICRU report 90. Key data for ionizing-radiation dosimetry: measurement standards and applications[R]. Oxford: ICRU, 2014. DOI: 10.1093/jicru/ndw029.
|
| [24] |
Vyšín L, Pachnerová Brabcová K, Štěpán V, et al. Proton-induced direct and indirect damage of plasmid DNA[J]. Radiat Environ Biophys, 2015, 54(3): 343-352. DOI:10.1007/s00411-015-0605-6 |
| [25] |
Garty G, Schulte R, Shchemelinin S, et al. A nanodosimetric model of radiation-induced clustered DNA damage yields[J]. Phys Med Biol, 2010, 55(3): 761-781. DOI:10.1088/0031-9155/55/3/015 |
| [26] |
Bordage MC, Bordes J, Edel S, et al. Implementation of new physics models for low energy electrons in liquid water in Geant4-DNA[J]. Phys Med, 2016, 32(12): 1833-1840. DOI:10.1016/j.ejmp.2016.10.006 |
| [27] |
Champion C, Incerti S, Aouchiche H, et al. A free-parameter theoretical model for describing the electron elastic scattering in water in the Geant4 toolkit[J]. Radiat Phys Chem, 2009, 78(9): 745-750. DOI:10.1016/j.radphyschem.2009.03.079 |
| [28] |
Champion C, Incerti S, Tran HN, et al. Geant4-DNA Collaboration. Electron and proton elastic scattering in water vapour[J]. Nucl Instrum Methods Phys Res B, 2012, 273: 98-101. DOI:10.1016/j.nimb.2011.07.049 |
| [29] |
Belli M, Cherubini R, Dalla Vecchia M, et al. DNA fragmentation in mammalian cells exposed to various light ions[J]. Adv Space Res, 2001, 27(2): 393-399. DOI:10.1016/s0273-1177(01)00007-2 |
| [30] |
Tran HN, Bitar ZE, Champion C, et al. Modeling proton and alpha elastic scattering in liquid water in Geant4-DNA[J]. Nucl Instrum Meth B, 2015, 343: 132-137. DOI:10.1016/j.nimb.2014.10.016 |
| [31] |
Garcia-Molina R, Abril I, Denton CD, et al. Calculated depth-dose distributions for H+ and He+ beams in liquid water[J]. Nucl Instrum Meth B, 2009, 267(16): 2647-2652. DOI:10.1016/j.nimb.2009.05.038 |
 2023, Vol. 43
2023, Vol. 43