2. 合肥综合性国家科学中心能源研究院 安徽省能源实验室, 合肥 230031
2. Institute of Energy, Hefei Comprehensive National Science Center, Anhui Energy Laboratory, Hefei 230031, China
钆具有天然丰度高(约为15.68%)、热中子截面大(约为55 000靶)、可实现诊疗一体化等优点,使得钆中子俘获治疗(gadolinium neutron capture therapy,157GdNCT)成为研究热点 [1]。它是利用热中子与富集于肿瘤组织的靶向药物中的157Gd发生中子俘获反应,产生γ射线、内转换电子(internal conversion electron,IC)以及俄歇电子(auger and coster-kroning,ACK)杀伤肿瘤细胞[2]。IC和高传能线密度(LET)的俄歇电子对肿瘤细胞具有较大的杀伤能力[3],但是估算这些低能电子的相对生物效应(relative biological effectiveness,RBE)是目前钆中子俘获治疗研究所面临的主要挑战[4]。
对于低能电子和X射线,采用线能等微剂量学参量可以更精确地确定RBE值,且线能本身能够被直接测定[5]。微剂量学参数可以使用组织等效正比计数器(tissue-equivalent proportional counter,TEPC)直接测量或者通过蒙特卡罗(Monte Carlo,MC)径迹结构计算程序模拟计算得到。但是使用TEPCs测量直径低于30 nm的微观体积中的能量分布时,其测量结果存在很大的不确定性。因此,要精确确定在纳米水平体积内部能量沉积的微观分布,主要使用蒙特卡罗径迹结构计算方法[4]。
本研究利用蒙特卡罗程序Geant4-DNA程序包模拟计算157GdNCT中产生的内转换电子和俄歇电子在径迹结构上的能量沉积分布情况,使用微剂量动力学模型(microdosimetric kinetic model,MKM)计算低能电子的RBE,并分析Geant4-DNA物理模型以及靶标体积等参量变化对模拟结果的影响。
材料与方法1.计算模型:Geant4是由欧洲核子中心(CERN)开发的一种开源蒙特卡罗应用软件包,用于模拟粒子在物质中输运的物理过程,被广泛地应用于放射医学、辐射防护、高能物理等领域[6-7]。为了模拟157GdNCT中产生的内转换电子和俄歇电子作用于DNA的过程,在Geant4-DNA软件包中提供了3种推荐的参考物理模型,用于模拟液态水中的离散电子相互作用,分别为G4EmDNAPhysics _ option2(option2)、G4EmDNAPhysics _ option4(option4)、G4EmDNAPhysics _ option6(option6),这3个物理模型使用不同的物理过程模拟电子相互作用[6]。但是option4的能量运用范围为10 eV~10 keV,不适合所研究的内转换电子和俄歇电子的能量大小,因此使用了特设物理模型G4EmDNAPhysics _ option7(option7),option7是结合了option4的物理过程(10 eV~10 keV)和option2高能电子的物理过程(10 keV~1 MeV)。在本研究中,option2、option6以及option7物理模型被用于计算钆中子俘获治疗释放低能电子的RBE值,并分析不同物理模型对RBE值的影响。
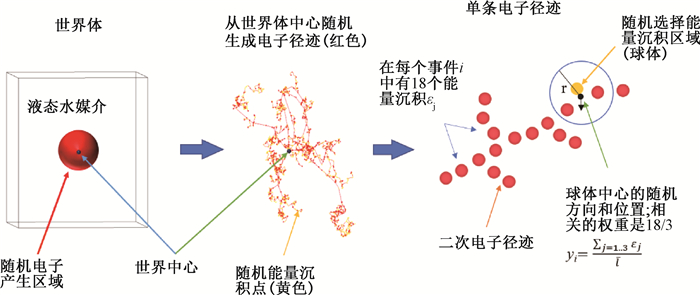
在模拟中建立一个长10 cm的正方体模型,以液态水填充。根据157GdNCT释放的内转换电子和俄歇电子的能谱[8],将其作为放射源,从模型中心随机方向发射。为了将计算结果的统计误差降至1%以下,初级电子数设置为5×106个,其模拟过程如图 1所示。在该模型中,每条径迹上随机选取半径为r的球体作为靶标体积,并统计靶标内的能量沉积情况。线能y是微剂量学中的重要物理量,它是指在一小体积元内由单次能量沉积事件造成的授予能同穿过该体积元随机排列平均弦长(
| $ y_i=\frac{\sum\limits_j \varepsilon_{i, j}}{\bar{l}} $ | (1) |
|
图 1 钆中子俘获治疗释放低能电子在液态水中模拟反应及单条径迹线能yi计算示意图 Figure 1 Diagramof simulated reaction of low energy electrons released by Gadolinium Neutron Capture Therapy in liquid water and of energy yi calculation for a track |
式中,授予能εi, j为第i条径迹上随机选取球体内j个能量沉积和,
在径迹结构空间范围内随机选取抽样位点是准确获取微剂量学参数中的重要一步。为了避免抽样偏向高密度能量沉积,在本研究的计算模型中,使用加权随机抽样方法对每条径迹选取抽样点,选取抽样点时不是均匀随机地选取径迹结构所在空间范围内的某一点,而是按照一定的概率直接随机选取能量沉积点,这个概率正比于该能量沉积点能量的大小。在本研究的计算模型中,对于每条径迹的线能yi均存在对应的频率加权因子fi,可使用以下表达式计算:
| $ f_i=\frac{\omega_i}{\sum _{i=1}^N \omega_i} $ | (2) |
式中,N为初级粒子径迹总数,ωi为每条径迹上所有能量沉积点能量与该径迹内随机选取靶内能量沉积点能量的比值。线能y是一个随机量,在指定的位点内存在一个分布,而f(y)是线能y的概率密度分布,揭示了线能y在目标中的随机分布。根据式(1)和(2),在计算模型中单次辐射事件的频率平均线能
| $ \bar{y}_F=\sum\limits_{i=1}^N y_i f_i $ | (3) |
由于上面公式可知,线能y与靶标体积大小密切相关。国际辐射单位与测量委员会(ICRU)第40号报告建议在直径1 μm球体中确定微剂量学中线能y的能谱,但研究表明,弦长约10 nm或更小的体积可以更好地反映局部微观能量沉积,也与放射生物学有效性更密切相关[9]。Goodhead[10]发现,ICRU建议体积(1 μm)大小并不适合揭示低能量俄歇电子的能量沉积模式,它们大部分能量沉积在很小的体积内。Lindborg等[11]已在直径为10~15 nm靶球体中利用微剂量学方法再现了临床RBE值。由于5~15 nm范围相当于直接作用(约10 bp或3~4 nm)和间接作用(自由扩散距离1~10 nm) 共同作用诱导DNA损伤产生DSB的假设敏感靶标[12]。因此,分别建立直径为6、10、15 nm的球体,假设为内转换电子和俄歇电子诱导DNA损伤产生DSB的敏感靶标。
2.计算方法:在辐射防护中,相对生物效应是指X射线或γ射线引起某一生物效应所需剂量与所观察的电离辐射引起相同生物效应所需剂量的比值[13]。本研究采用微剂量动力学模型计算钆中子俘获治疗中释放低能电子的RBE。
根据改进的非泊松(non-Poisson)分布的MKM理论[14],以人唾液腺细胞(HSG)在200 kVp的X射线照射后存活10%作为生物学终点,使用下列表达式计算157GdNCT中释放内转换电子和俄歇电子的相对生物效应[12]:
| $ R B E=\frac{D_P}{D_P^{\prime}}=\frac{D_P}{\frac{-\alpha+\sqrt{\alpha^2-4 \ln (P)}}{2 \beta}} $ | (4) |
式中,DP=5 Gy,为人唾液腺细胞在200 kVp的X射线照射后存活P=10%所需的剂量[15];D′ P为指钆中子俘获反应中产生内转换电子和俄歇电子使HSG细胞存活10%时所需的剂量;α、β分别为一次项系数和二次项系数。β在MKM模型中是一个与辐射品质无关常量,对于HSG细胞β=0.05 Gy-2,而α在MKM模型中按照如下公式计算[16]:
| $\alpha=\alpha_0+\frac{\beta}{\rho \pi r_d^2} y^* $ | (5) |
| $ y^*=y_0^2 \frac{\int\left(1-\exp \left(-y^2 / y_0^2\right)\right) f(y) \mathrm{d}(y)}{\bar{y}_F} $ | (6) |
| $ \bar{y}_F=\int y f(y) \mathrm{d} y $ | (7) |
式中,参数α0、y0为MKM的模型参数,y*为利用饱和度参数y0修正的剂量平均线能。根据本研究计算模型中使用的加权随机抽样方法,结合上述式(3)、式(6)和(7),获得剂量平均线能y*在该计算模型中的关系式为:
| $y^*=y_0^2 \sum\limits_{i=1}^N \frac{1-\exp \left(-y_i^2 / y_0^2\right)}{y_i} $ | (8) |
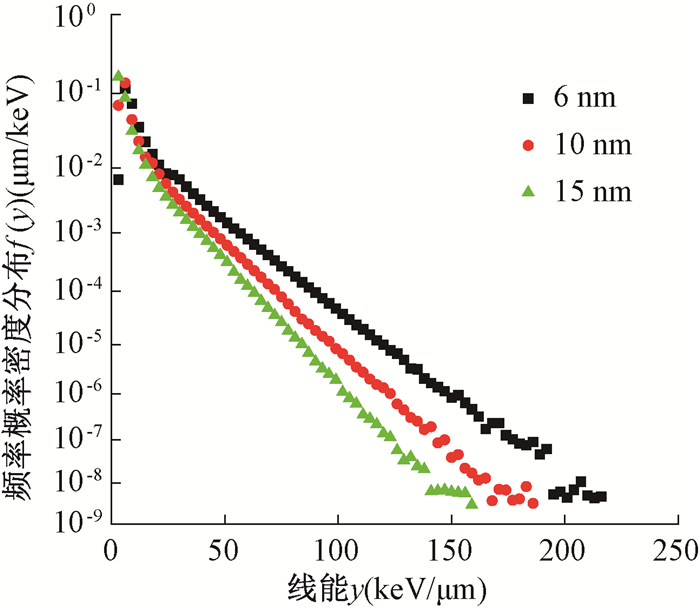
1.敏感靶标体积的影响:在物理模型为option2的情况下,图 2是敏感靶标直径分别为6、10、15 nm时线能y在目标中的概率密度分布f(y),揭示线能y在目标体积中的随机分布,表 1是在不同敏感靶标直径下线能y等相关物理量的结果。
|
图 2 不同敏感靶标直径下的频率概率密度分布f(y) Figure 2 Frequency probability density distributions f(y) for different sensitive target diameters |
|
|
表 1 线能在不同敏感靶标直径下的结果(keV/μm) Table 1 The results of line energy at different sensitive target diameters(keV/μm) |
表 2是以微剂量动力学模型中参数α0=0.077 7 Gy-1,y0=108 keV/μm作为确定的物理量[16],计算157GdNCT中释放内转换电子和俄歇电子RBE值在物理模型option2下不同敏感靶标直径中的比较,差异百分比是以敏感靶标直径6 nm为参考,分别获得敏感靶标直径10 nm和15 nm的对比结果。以敏感靶标直径6 nm的RBE值为参考,RBE在敏感靶标直径10 nm相比于6 nm差异百分比为13%,而直径15 nm相比于6 nm的差异百分比高达21%。
|
|
表 2 RBE在不同敏感靶标直径下的值 Table 2 The values of RBE at different sensitive target diameters |
2.Geant4-DNA物理模型的影响:表 3是选取敏感靶标直径为10 nm时,内转换电子和俄歇电子在不同物理模型下线能y等相关物理量的结果。表 4是基于微剂量动力学模型,在敏感靶标直径为10 nm下,比较了内转换电子和俄歇电子在不同物理模型中的RBE值变化,差异百分比是以物理模型option2为参考,分别获得物理模型option6和option7的对比结果。以物理模型option2的RBE值1.53作为参考,option6和option7相对于option2的差异百分比分别为2.6%和0.6%。
|
|
表 3 线能在不同物理模型下的结果(keV/μm) Table 3 The results of line energy in different physical models(keV/μm) |
|
|
表 4 不同物理模型的RBE值 Table 4 The values of RBE for different physical models |
讨论
在本研究中,利用蒙特卡罗程序Geant4-DNA模拟计算了157GdNCT中释放的内转换电子和俄歇电子的相对生物效应值,并分析了敏感靶标体积以及3种Geant4-DNA物理模型对RBE值的影响。模拟中假设157GdNCT中释放的内转换电子和俄歇电子随机分布在DNA内,利用加权随机抽样方法在每条电子径迹上随机选取球体作为敏感靶标,计算每条径迹上随机选取的球体内所有能量的沉积。使用了加权因子避免采样偏向高密度能量沉积[12],使线能等相关物理量模拟结果不会偏向高密度能量沉积。并利用微剂量动力模型计算了内转换电子和俄歇电子的相对生物效应,直观地评价157GdNCT中释放的内转换电子和俄歇电子在DNA内引起的生物效应。
结果显示,敏感靶标体积直径越大,线能y在目标体积中概率密度分布f(y)越小。在直径6 nm的敏感靶标中,线能y为19.23 keV/μm,敏感靶标中的平均授予能为115.38 eV,相当于在直径为6 nm的敏感靶标中能量沉积密度为1.02 eV/nm3;而直径15 nm的敏感靶标中线能y是12.64 keV/μm,平均授予能是189.6 eV,此时相当于在敏感靶标内能量沉积密度是0.11 eV/nm3。因此,随着敏感靶标体积的增大,每纳米体积内沉积的能量减小。不同敏感靶标直径的RBE差异较大,且随着敏感靶标体积增大而减小。以敏感靶标直径6 nm的RBE值1.77为参考,内转换电子和俄歇电子在敏感靶标直径10 nm的RBE为1.53,相比于6 nm的差异百分比为13%,而直径15 nm的RBE相比于6 nm的差异百分比高达21%。Golshani等[8]基于微剂量动力学模型计算方法,计算内转换电子和俄歇电子位于在直径为10 nm的圆柱形靶的中心时,RBE值为1.89,而位于圆柱形靶外表面1 nm处时的RBE值为1.53。从结果可知,生物效应不仅取决于电离辐射的剂量率效应,更取决于能量沉积的空间分布情况。尽管在同一电离辐射下,平均授予能和平均弦长的变化引起了线能y的变化,但是线能y在敏感靶标内空间分布的减小,导致RBE值的减小。因此,敏感靶标体积在模拟中对157GdNCT中释放的内转换电子和俄歇电子的RBE值影响较大。
RBE作为不同种类电离辐射产生的生物学效应的一个直观指标,线能y和RBE在上述几种Geant4-DNA物理模型下RBE值差异较小。以物理模型option2的RBE值1.53为参考,option6和option7的RBE值相比于option2的差异百分比分别为2.6%和0.6%。Geant4-DNA物理模型option6采用了与option2和option7不同的非弹性过程,虽然option6在亚keV下有更高的电离和激发截面,更高的弹性截面导致了更小的平均自由路径和更密集的能量消耗空间模式,但是其能量运用范围仅为11 eV~256 keV,相比于物理过程option2和option7的能量运用范围较小[12],根据157GdNCT期间释放的内转换电子和俄歇电子的发射光谱,反应过程中存在电子能量超出option6的能量运用范围,导致能量高于256 keV的离散电子运输无法发生。而option7和option2的RBE值差异百分比最小,原因是两者采用了相似的非弹性过程,option2包含着振动激发和电子附着过程,option7不包含该过程[12]。因此,由不同物理模型下的RBE值差异得出,模拟中物理模型对157GdNCT释放的内转换电子和俄歇电子的RBE值影响较小。
综上,本研究结果表明,157GdNCT释放的内转换电子和俄歇电子在DNA内的模拟反应过程中,敏感靶标体积对其相对生物效应具有较大的影响,相对生物效应随着敏感靶标体积增大而减小,而Geant4-DNA物理模型对其相对生物效应的影响较小。因此,在Geant4-DNA模拟计算157GdNCT释放低能电子的相对生物效应中在径迹上抽样选取敏感靶标体积大小时需要仔细考虑。
利益冲突 所有作者没有任何利益冲突,未接受任何不当的职务和财务利益
作者贡献声明 余威悦负责研究实施、论文撰写及修改;洪兵负责指导研究方案和论文修改;卢棚、梁立振负责指导论文修改;陈妮负责指导研究课题进展和论文修改
| [1] |
Ho SL, Yue H, Tegafaw T, et al. Gadolinium neutron capture therapy (GdNCT) agents from molecular to nano: current status and perspectives[J]. ACS Omega, 2022, 7(3): 2533-2553. DOI:10.1021/acsomega.1c06603 |
| [2] |
De Stasio G, Rajesh D, Casalbore P, et al. Are gadolinium contrast agents suitable for gadolinium neutron capture therapy?[J]. Neurol Res, 2005, 27(4): 387-398. DOI:10.1179/016164105X17206 |
| [3] |
Goorley T, Nikjoo H. Electron and photon spectra for three gadolinium-based cancer therapy approaches[J]. Radiat Res, 2000, 154(5): 556-563. DOI:10.1667/0033-7587(2000)154[0556:eapsft]2.0.co;2 |
| [4] |
Golshani M, Mowlavi AA, Azadegan B. Computational assessment of the cellular dosimetry and microdosimetry of the gadolinium electrons released during neutron capture therapy[J]. Biomed Phys Eng Expr, 2019, 5(2): 25031. DOI:10.1088/2057-1976/aaec33 |
| [5] |
傅玉川. 从微剂量学到纳米剂量学—连接放射生物和辐射物理的桥梁[J]. 生物医学工程学杂志, 2014, 31(3): 703-707. Fu YC. From microdosimetry to nanodosimetry—the link between radiobiology and radiation physics[J]. J Biomed Eng, 2014, 31(3): 703-707. DOI:10.7507/1001-5515.20140131 |
| [6] |
Incerti S, Kyriakou I, Bernal MA, et al. Geant4-DNA example applications for track structure simulations in liquid water: a report from the Geant4-DNA project[J]. Med Phys, 2018, 45(8): e722-e739. DOI:10.1002/mp.13048 |
| [7] |
Incerti S, Ivanchenko A, Karamitros M, et al. Comparison of GEANT4 very low energy cross section models with experimental data in water[J]. Med Phys, 2010, 37(9): 4692-4708. DOI:10.1118/1.3476457 |
| [8] |
Golshani M, Azadegan B, Mowlavi AA. Microdosimetry calculations and estimation of the relative biological effectiveness of the low-energy electrons released during Gd neutron capture reaction[J]. Radiat Phys Chem, 2021, 188: 109585. DOI:10.1016/j.radphyschem.2021.109585 |
| [9] |
International Commission on Radiation Units and Measurements. ICRU Report 40. The quality factor in radiation protection[R]. Bethesda: ICRU, 1986.
|
| [10] |
Goodhead DT. Biological effectiveness of lower-energy photons for cancer risk[J]. Radiat Prot Dosim, 2019, 183(1-2): 197-202. DOI:10.1093/rpd/ncy246 |
| [11] |
Lindborg L, Hultqvist M, Carlsson TÅ, et al. Lineal energy and radiation quality in radiation therapy: model calculations and comparison with experiment[J]. Phys Med Biol, 2013, 58(10): 3089-3105. DOI:10.1088/0031-9155/58/10/3089 |
| [12] |
Kyriakou I, Emfietzoglou D, Ivanchenko V. Microdosimetry of electrons in liquid water using the low-energy models of Geant4[J]. J Appl Phys, 2017, 122(2): 24303. DOI:10.1063/1.4992076 |
| [13] |
Task Group on Radiation Quality Effects in Radiological Protection, Committee 1 on Radiation Effects, International Commission on Radiological Protection. ICRP Publication No. 92. Relative biological effectiveness (RBE), quality factor (Q), and radiation weighting factor (wR)[J]. Ann ICRP, 2003, 33(4): 1-117. DOI:10.1016/s0146-6453(03)00024-1 |
| [14] |
Kase Y, Kanai T, Matsumoto Y, et al. Microdosimetric measurements and estimation of human cell survival for heavy-ion beams[J]. Radiat Res, 2006, 166(4): 629-638. DOI:10.1667/RR0536.1 |
| [15] |
Sato T, Kase Y, Watanabe R, et al. Biological dose estimation for charged-particle therapy using an improved PHITS code coupled with a microdosimetric kinetic model[J]. Radiat Res, 2009, 171(1): 107-117. DOI:10.1667/RR1510.1 |
| [16] |
Hawkins RB. A microdosimetric-kinetic model for the effect of non-Poisson distribution of lethal lesions on the variation of RBE with LET[J]. Radiat Res, 2003, 160(1): 61-69. DOI:10.1667/rr3010 |
 2023, Vol. 43
2023, Vol. 43


