2. 中国科学院大学, 北京 100049;
3. 四川大学华西医院医学装备创新研究中心, 成都 610041
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Medical equipment Innovation Research Center, West China Hospital, Sichuan University, Chengdu 610041, China
准确的相对生物效应(relative biological effectiveness,RBE)计算对临床应用具有十分重要的意义。为了最大化地发挥质子重离子治疗的剂量学优势,多种RBE模型被提出用来预测肿瘤患者体内体素化的RBE值分布。局部效应模型(local effect model,LEM)[1-4]和微剂量动力学模型(microdosimetric kinetic model,MKM)[5-8]是目前临床应用最为广泛的两个生物效应模型。MKM由Hawkins等[5]基于双重辐射作用理论[9]提出。MKM中认为细胞核中存在着许多亚细胞辐射敏感区域,称之为敏感域。敏感域的单次事件剂量加权平均比能是MKM计算中的关键物理量。一方面可以通过组织等效正比计数器(tissue equivalent proportional chamber,TEPC)获取粒子在敏感域内的线能谱,从而计算得到敏感域的单次事件剂量加权平均线能。另一方面Kase等[10]直接基于粒子径迹结构模型计算粒子在敏感域内的单次事件剂量加权平均比能用于MKM计算。Inaniwa等[11]将此计算方法成功植入日本千叶县碳离子治疗装置(heavy ion medical accelerators in Chiba, HIMAC)的治疗计划系统并用于临床。但是,Kase等[10]和Inaniwa等[11]在计算敏感域的单次事件剂量加权平均比能时,都将敏感域假定为圆柱状,以简化积分计算过程。
本研究为了探究敏感域形状对MKM参数的影响,分别假定敏感域为圆柱状和球状,编写了带电粒子分别在两种形状敏感域内单次事件剂量加权平均比能的计算程序,通过D10计算值与实验值的拟合确定了两种不同形状敏感域对应的MKM参数并进行了比较。
材料与方法1.MKM计算公式:一个带电粒子穿过敏感域或其临近区域并在其中沉积能量,称为该粒子在敏感域中产生了一次能量沉积事件,本研究接下来的部分都将能量沉积事件简称为事件。敏感域内产生事件数目为0的概率称为该敏感域的存活率。假设一个敏感域的比能用zd表示,其存活率用sd表示,根据线性平方模型可得二者的关系式:
| $ s_{\mathrm{d}}=\mathrm{e}^{-A z_{\mathrm{d}}-B z_{\mathrm{d}}{ }^2} $ | (1) |
式中,A和B分别为线性平方模型中的一次项系数和二次项系数。式(1) 是在微观尺度上对敏感域存活率与比能关系的描述,其中比能是随机量。而在MKM的实际应用中,需要得到细胞存活率S和宏观吸收剂量D的关系。Kase等[10]给出如下计算公式:
| $ S=\mathrm{e}^{-\left(\alpha_0+\beta \bar{z}_{1, \mathrm{~d}}\right) D-\beta D^2} $ | (2) |
式中,z1,d为敏感域的单次事件剂量加权平均比能;α0为LET = 0时细胞存活曲线的初始斜率;β为一个与辐射类型无关的常量。根据国际辐射单位与测量委员会(ICRU)第36号报告[12],可知敏感域内单次事件剂量加权平均比能的定义为:
| $ \bar{z}_{1, \mathrm{~d}}=\frac{\int_0^{\infty} z_{1, \mathrm{~d}}{ }^2 f_1\left(z_{1, \mathrm{~d}}\right) \mathrm{d} z_{1, \mathrm{~d}}}{\int_0^{\infty} z_{1, \mathrm{~d}} f_1\left(z_{1, \mathrm{~d}}\right) \mathrm{d} z_{1, \mathrm{~d}}} $ | (3) |
式中,f1 (z1, d) 为敏感域内单次事件比能z1, d的概率密度。考虑到高LET照射下饱和效应的存在,Kase等[13]给出了饱和效应修正后敏感域的单次事件剂量加权平均比能(z 1,d *) 的计算公式,即:
| $ \bar{z}_{1, \mathrm{~d}}{ }^*=\frac{z_0^2 \int_0^{\infty}\left(1-\mathrm{e}^{-\left(z_{1, \mathrm{~d}}/ z_0\right)^2}\right) f_1\left(z_{1, \mathrm{~d}}\right) \mathrm{d} z_{1, \mathrm{~d}}}{\int_0^{\infty} z_{1, \mathrm{~d}} f_1\left(z_{1, \mathrm{~d}}\right) \mathrm{d} z_{1, \mathrm{~d}}} $ | (4) |
式中,z0为一个常量,可由细胞核半径Rn、敏感域半径rd,以及β计算得出:
| $ z_0=\frac{\left(R_n / r_{\mathrm{d}}\right)^2}{\sqrt{\beta\left(1+\left(R_n / r_{\mathrm{d}}\right)^2\right)}} $ | (5) |
因此,细胞存活率S的最终计算表达式为:
| $ S=\mathrm{e}^{-\left(\alpha_0+\beta \bar{z}_{1, \mathrm{~d}}\,^*\right) D-\beta D^2} $ | (6) |
根据式(6)可以得到使得被照射细胞存活率为10%时,所需射线的照射剂量,即D10:
| $ \begin{gathered} D_{10}= \\ \frac{-\left(\alpha_0+\beta \bar{z}_{1, \mathrm{~d}}{ }^*\right)+\sqrt{\left(\alpha_0+\beta \bar{z}_{1, \mathrm{~d}}{ }^*\right)^2-4 \alpha_0 \cdot \ln 0.1 \cdot \beta}}{2 \beta} \end{gathered} $ | (7) |
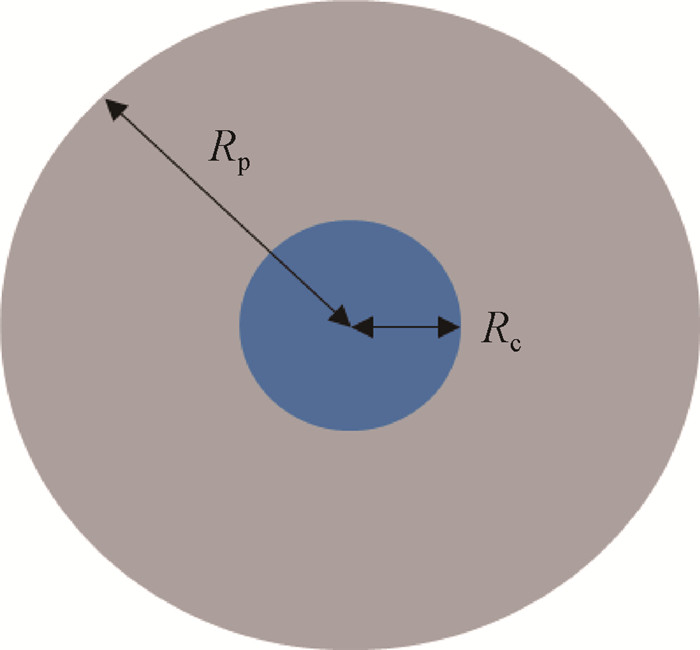
2.径迹结构模型:计算敏感域的单次事件剂量加权平均比能,需要引入带电粒子的径迹结构模型。带电粒子的径迹结构模型可用于描述该粒子辐射的剂量分布。当带电粒子在极小的体积中沉积能量时,粒子穿过的路径被视作线段,并且认为在这段路径上粒子速度不发生变化。如图 1所示,在径向上,径迹结构由两部分组成,内圆部分描述初始入射粒子对剂量沉积的贡献,此处被称为核心区域;外面圆环部分描述由次级电子作用对剂量沉积的贡献,称为半影区域。Kase等[10]采用的径迹结构模型中,半影区域半径Rp以及该区域的剂量分布函数通过Kiefer和Straaten[14]给出的公式计算,核心区域半径Rc和该区域的均匀剂量分布通过Chatterjee和Schaefer[15]给出的公式计算,因此该径迹结构模型也被称为Kiefer-Chatterjee模型。
|
注:Rc. 核心区域半径;Rp. 半影区域半径 图 1 带电粒子径迹结构横截面示意图 Figure 1 Schematic of the cross-section of a charged particle track structure |
3.敏感域的单次事件剂量加权平均比能的计算:在MKM中,敏感域的形状和大小会影响到单次事件剂量加权平均比能的计算结果,甚至进一步影响MKM对辐射生物效应的预测。根据获得的细胞照射实验数据[16]结合MKM计算结果通过最小二乘法得到敏感域尺寸以及细胞核尺寸的拟合值。在Kiefer-Chatterjee径迹结构模型中,其核心部分相当于一个半径极小的实心圆柱体,其中呈均匀剂量分布;而半影部分相当于包裹着核心部分的圆柱外壳。带电粒子通过敏感域时沉积的能量,可以通过计算径迹结构与敏感域相贯体积上的积分获得。使用圆柱体作为敏感域的形状可以简化积分计算,这是由于假定带电粒子在径迹结构的轴向即粒子入射方向不发生速度变化,此时敏感域与径迹结构模型的相贯体积上的积分可被视为平面上的二维积分与长度的乘积,其长度对计算结果不产生影响,通常被看作等同于圆柱体底面的直径。本研究编写了圆柱状敏感域的比能计算程序,所涉及到的二重积分通过MATLAB(Matrix Laboratory)里的符号积分函数实现。将球体作为敏感域的形状时,就需要计算球体和径迹结构模型相贯体积上的三重积分,相比前者计算过程要变得复杂一些。球体敏感域的比能计算所涉及到的三重积分通过MATLAB里的数值积分函数实现。对于两种形状的敏感域,都假定所有带电粒子平行入射。对于圆柱状敏感域,粒子入射方向平行于其中心轴。对于球状敏感域,粒子入射方向上球体直径所在直线即为该方向上的中心轴。将径迹结构模型的中心轴到敏感域中心轴的距离,称为碰撞参数(impact parameter)。给定粒子种类和能量以及敏感域尺寸后,此时敏感域内比能只取决于碰撞参数。碰撞参数越小,敏感域内的比能越大。当碰撞参数为0时,对应带电粒子沿敏感域的中心轴入射的情况,此时敏感域内的比能最大。当碰撞参数为x时,其单次事件比能为z1, d(x),对应概率为
| $ \begin{gathered} \bar{z}_{1, \mathrm{~d}}{ }^*=\frac{z_0^2 \int_0^{x_{\max }}\left(1-\mathrm{e}^{-\left(z_{1, \mathrm{~d}}(x) / z_0\right)^2}\right) f_1(x) \mathrm{d} x}{\int_0^{x_{\max }} z_{1, \mathrm{~d}}(x) f_1(x) \mathrm{d} x} \\ =\frac{z_0{ }^2 \int_0^{x_{\max }}\left(1-\mathrm{e}^{-\left(z_{1, \mathrm{~d}}(x) / z_0\right)^2}\right)\left(\frac{2 \pi x}{\int_0^{x_{\max }} 2 \pi x \mathrm{~d} x}\right) \mathrm{d} x}{\int_0^{x_{\max }} z_{1, \mathrm{~d}}(x)\left(\frac{2 \pi x}{\int_0^{x_{\max }} 2 \pi x \mathrm{~d} x}\right) \mathrm{d} x} \\ =\frac{z_0^2 \int_0^{x_{\max }}\left(1-\mathrm{e}^{-\left(z_{1, \mathrm{~d}}(x) / z_0\right)^2}\right) 2 \pi x \mathrm{~d} x}{\int_0^{x_{\max }} z_{1, \mathrm{~d}}(x) 2 \pi x \mathrm{~d} x} \end{gathered} $ | (8) |
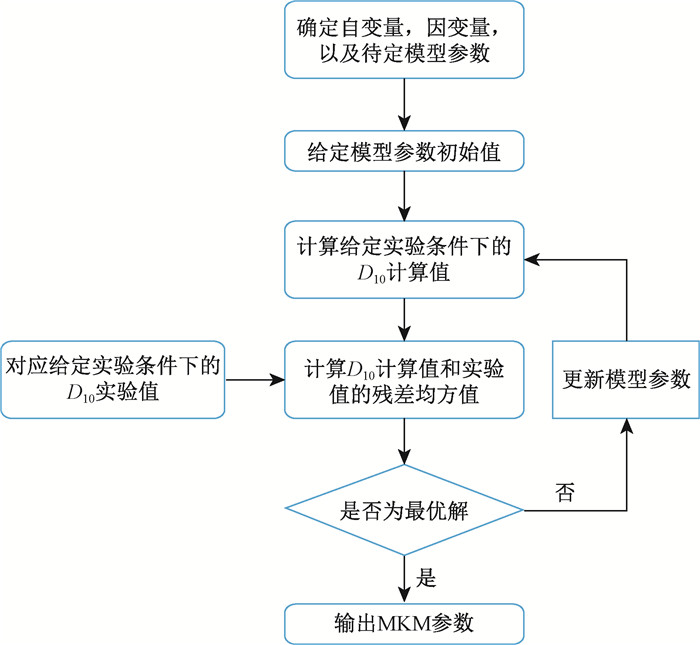
4. MKM参数的确定:MKM所需模型参数为敏感域半径rd,细胞核半径Rn,以及α0和β。β在本文中被视为常量,并且HSG细胞和V79细胞各自对应的β值与Furusawa等[16]保持一致,其余待定参数也仅与被照射细胞类型有关,与辐射类型无关。分别假定敏感域为圆柱状和球状,基于3He、12C、20Ne分别照射HSG细胞和V79细胞获得的实验数据, 以3种粒子的核电荷数、动能及其对应传能线密度(LET)作为自变量,D10值为因变量,并以D10计算值与实验值的残差均方值J2为优化目标,给定合理初值后利用最小二乘法经过足够次数迭代后获得的最终拟合结果即为最优模型参数。整个参数优化的实现利用MATLAB里的非线性拟合函数nlinfit完成,由于细胞实验数据中可能存在异常值影响拟合结果,在nlinfit里选择稳健拟合选项,权重函数为talwar函数:残差>1的数据权重为0,残差<1时权重为1。参数优化的整体流程图如图 2所示。
|
注:D10.使被照射细胞存活率达到10%时所需射线剂量;MKM.微剂量动力学模型 图 2 MKM参数优化流程图 Figure 2 Flow Chart of MKM Parameter Optimization |
结果
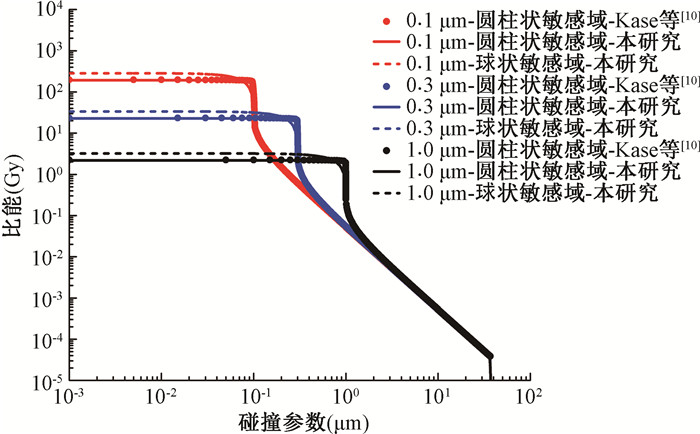
1.不同碰撞参数下敏感域的比能:图 3显示了不同碰撞参数下,带电粒子在两种形状敏感域内沉积比能的变化关系。对于圆柱状敏感域,底半径分别为0.1、0.3和1.0 μm,对应高分别为0.2、0.6和2.0 μm。对于球状敏感域,半径分别为0.1、0.3和1.0 μm。带电粒子为能量为43 MeV/u的碳离子,其对应LET为50 keV/μm。圆点数据为Kase等[10]提供的碳离子通过圆柱状敏感域在不同碰撞参数下比能的计算值,实线为本研究采用圆柱状敏感域的计算结果。两者较好的吻合表明,可以很好地再现Kase等[10]关于敏感域内比能的计算方法。虚线表示球状敏感域内比能的计算结果。对比结果显示,相同带电粒子分别通过相等半径尺寸的圆柱状敏感域和球状敏感域,在相同的碰撞参数下,球状敏感域中的比能高于前者,尤其是在碰撞参数较小的时候。
|
图 3 43 MeV/u的碳离子在3种不同尺寸的体积内沉积比能的比较 Figure 3 Comparison of the specific energy in three different volumes for carbon ion with an energy of 43 MeV/u |
2.两种细胞的MKM参数:根据材料与方法部分所述步骤完成了两种细胞的MKM参数的优化,最终所得MKM参数如表 1所示,其中加入了Inaniwa和Kanematsu[17]给出的参数展示。根据表 1可知,拟合所得敏感域半径相差不大,而细胞核的半径相差较大,并且采用球状敏感域拟合得到的细胞核半径值明显高于采用圆柱状敏感域所得。根据荧光显微镜的观察,HSG细胞核和V79细胞核尺寸分别在6.0和4.5 μm左右[18],采用球状敏感域计算拟合得到的细胞核尺寸相对更接近于上述观察值。J2为D10计算值与实验值的残差均方值,无论对于哪种细胞,两种敏感域的计算结果与对应实验数据的拟合优度都十分接近。
|
|
表 1 HSG细胞和V79细胞的MKM参数 Table 1 MKM parameters of HSG cells and V79 cells |
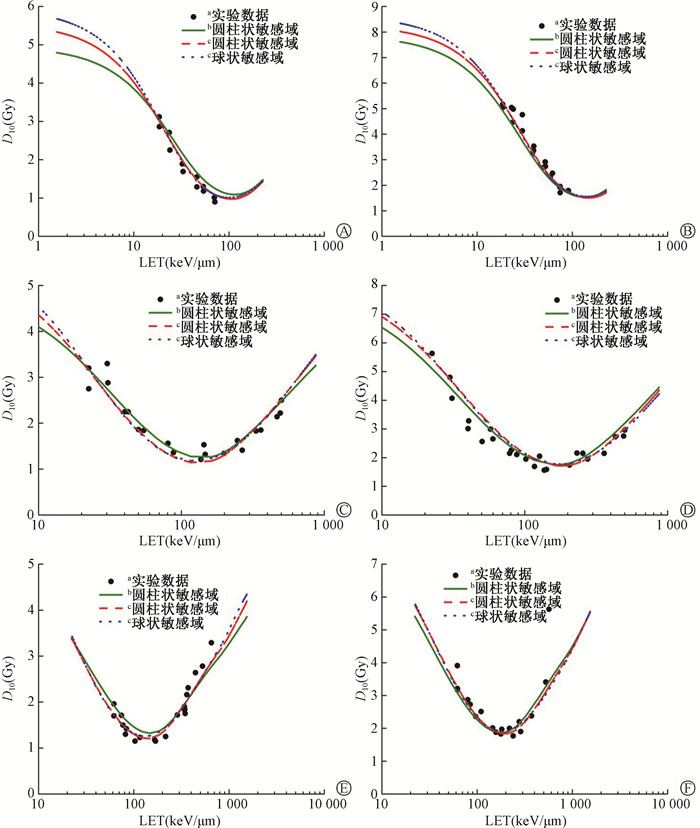
3. 3种粒子照射两种细胞的D10-LET关系:确定了MKM参数后,可以根据敏感域和细胞核尺寸的拟合值计算3种粒子在两种形状敏感域的饱和效应修正单次事件剂量加权平均比能。接着根据公式(7)可以计算得到相应的D10。图 4展示了3种粒子分别照射HSG细胞和V79细胞的D10和粒子LET的关系。其中黑色圆点数据来源于Furusawa等[16]采用3种带电粒子在含氧情况下分别照射HSG细胞和V79细胞获得的实验结果。绿色实线表示将Inaniwa和Kanematsu[17]给出的MKM参数运用到本文所用计算程序后所得计算结果,敏感域为圆柱状。红色虚线表示本研究采用圆柱状敏感域所得模型参数的计算结果,蓝色点线表示球状敏感域的。其中3种粒子的动能及对应LET数据来源于ICRU发布的第49号报告[19]和第73号报告[20]。当照射粒子的LET范围大约在20 ~700 keV/μm时,尽管采用的模型及其对应参数不同,但都与实验结果比较吻合。粒子LET低于20 keV/μm时,无论是HSG细胞还是V79细胞,球状敏感域对应的D10计算曲线都明显高于圆柱状敏感域的。低LET区域的实验数据较少,质子照射细胞的实验数据可以用来进一步比较两者拟合的差异。当粒子LET高于700 keV/μm时,对于HSG细胞,球状敏感域计算得到的D10略高于圆柱状敏感域的,对于V79细胞,二者相差不大。
|
注:a Furusawa等[16];bInaniwa和Kanematsu [17]参数;c本研究;LET.传能线密度 图 4 3He、12C、20Ne照射HSG细胞和V79细胞的LET-D10关系A. 3He-HSG;B. 3He-V79;C. 12C-HSG;D. 12C-V79;E.20Ne-HSG;F.20Ne-V79 Figure 4 LET-D10 relationships for HSG cells and V79 cells exposed to 3He, 12C, 20Ne A. 3He-HSG; B. 3He-V79;C. 12C-HSG; D. 12C-V79;E.20Ne-HSG; F.20Ne-V79 |
讨论
计算带电粒子在较小敏感体积尤其是球状敏感体积内沉积的能量,有很多方法可以实现。Olko和Booz[21]引入一个类费米函数计算球状敏感区域内的沉积能量,这种方法考虑到了粒子在较小敏感体积内能量损失的涨落,但是其适用范围较窄,只给出了几种粒子0.3~5.0 MeV/u的数据。而更宽能量范围的数据,会更适用于辐射生物效应的计算。Sato和Furusawa[18]在其提出的双随机性微剂量动力学模型(double stochastic microdosimetric kinetic model,DSMKM)中,借助于蒙特卡罗程序粒子和重离子传输代码系统(particle and heavy ion transport code system,PHITS)计算了球状敏感域的单次事件剂量加权平均比能。与上述方法不同,本研究基于径迹结构模型计算球状敏感域的单次事件剂量加权平均比能,是对敏感域相关区域(径迹结构与敏感域的碰撞参数从0到xmax的区域)的全径迹结构平均,是理想情况下的概率加权平均,其缺点是忽略了能量损失的涨落,但其计算无需借助实验探测以及蒙特卡罗模拟,能够更容易地应用于质子或者重离子治疗计划系统。Kase等[10]和Inaniwa等[11]采用积分计算进行了径迹结构模型计算圆柱状敏感域内的单次事件剂量加权平均比能,本研究借助MATLAB完成了径迹结构模型计算球状敏感域内的单次事件剂量加权平均比能,是对其工作的补充与拓展。
放射生物学上认为,细胞核里存在许多对辐射敏感的靶点,带电粒子在敏感域中沉积能量,才会造成对细胞的损伤,在MKM模型将这些靶点称之为敏感域。MKM将敏感域假定为圆柱状或球状,是为了计算敏感域内的单次事件剂量加权平均比能时便于进行积分计算。根据参数拟合所得结果来看,圆柱状敏感域和球状敏感域的半径相当,并且圆柱状敏感域的长度通常被假定为等同于其直径。对于敏感域的形状选取,非旋转体不适用于本研究的计算,这是由于非旋转体敏感域与径迹结构模型在不同碰撞参数下的比能计算难以实现。本研究也曾将敏感域假定为双轴椭球状(3条轴中有两条轴相等的椭球体)进行计算,但是拟合所得椭球状敏感域的尺寸等同于球体,所以未曾加入本文进行比较。通过拟合得到的敏感域半径相当,而拟合得到的细胞核半径存在明显差异,根据球状敏感域拟合所得的两种细胞核半径相对更接近于实验观察值。除了细胞核尺寸外,其形态同样可以被直接观察得到,其中大多数细胞核呈球状或椭球状,但是本文并未对细胞核形状进行假定,这是由于细胞核形状对本研究的计算不产生影响,其半径Rp仅参与z0的计算。在后续研究中,会将细胞核的形状因素也考虑进去,获取更为准确的多种细胞核半径实验观察值,可能会对提高MKM对辐射生物效应的预测精度有帮助。
通过材料与方法部分中所述最小二乘法拟合得到敏感域半径和细胞核半径后,可以计算相关带电粒子(Z=1~10)在不同动能(0.1~1 000 MeV/u) 情况下在敏感域内的饱和效应修正后的单次事件剂量加权平均比能,接着按照粒子种类分别制表,然后结合蒙特卡罗模拟程序Geant4(GEometry ANd Tracking)即可得到治疗计划中患者体内每个网格内的饱和效应修正后的单次事件剂量加权平均比能,
本研究对采用粒子径迹结构模型计算两种形状敏感域的单次事件剂量加权平均比能进行了阐述,通过稳健最小二乘法分别拟合确定了两种细胞内的两种形状敏感域对应的MKM参数,比较了敏感域的形状对MKM参数的影响。
利益冲突 无
志谢 感谢Kase教授提供了不同碰撞参数下圆柱状域内比能的计算数据并提出了宝贵建议
作者贡献声明 严南负责论文撰写;周云、孙向上、廖文涛、刘俊雅参与研究;蒲越虎指导论文修改
| [1] |
Scholz M, Kraft G. Track structure and the calculation of biological effects of heavy charged particles[J]. Adv Space Res, 1996, 18(1-2): 5-14. DOI:10.1016/0273-1177(95)00784-c |
| [2] |
Elsässer T, Scholz M. Cluster effects within the local effect model[J]. Radiat Res, 2007, 167(3): 319-329. DOI:10.1667/RR0467.1 |
| [3] |
Elsässer T, Krämer M, Scholz M. Accuracy of the local effect model for the prediction of biologic effects of carbon ion beams in vitro and in vivo[J]. Int J Radiat Oncol Biol Phys, 2008, 71(3): 866-872. DOI:10.1016/j.ijrobp.2008.02.037 |
| [4] |
Elsässer T, Weyrather WK, Friedrich T, et al. Quantification of the relative biological effectiveness for ion beam radiotherapy: direct experimental comparison of proton and carbon ion beams and a novel approach for treatment planning[J]. Int J Radiat Oncol Biol Phys, 2010, 78(4): 1177-1183. DOI:10.1016/j.ijrobp.2010.05.014 |
| [5] |
Hawkins RB. A statistical theory of cell killing by radiation of varying linear energy transfer[J]. Radiat Res, 1994, 140(3): 366-374. |
| [6] |
Hawkins RB. A microdosimetric-kinetic model of cell death from exposure to ionizing radiation of any LET, with experimental and clinical applications[J]. Int J Radiat Biol, 1996, 69(6): 739-755. DOI:10.1080/095530096145481 |
| [7] |
Hawkins RB. A microdosimetric-kinetic theory of the dependence of the RBE for cell death on LET[J]. Med Phys, 1998, 25(7 Pt 1): 1157-1170. DOI:10.1118/1.598307 |
| [8] |
Hawkins RB. A microdosimetric-kinetic model for the effect of non-Poisson distribution of lethal lesions on the variation of RBE with LET[J]. Radiat Res, 2003, 160(1): 61-69. DOI:10.1667/rr3010 |
| [9] |
Kellerer AM, Rossi HH. The theory of dual radiation action[J]. Curr Top Radiat Res, 1972, 8(2): 85-185. |
| [10] |
Kase Y, Kanai T, Matsufuji N, et al. Biophysical calculation of cell survival probabilities using amorphous track structure models for heavy-ion irradiation[J]. Phys Med Biol, 2008, 53(1): 37-59. DOI:10.1088/0031-9155/53/1/003 |
| [11] |
Inaniwa T, Furukawa T, Kase Y, et al. Treatment planning for a scanned carbon beam with a modified microdosimetric kinetic model[J]. Phys Med Biol, 2010, 55(22): 6721-6737. DOI:10.1088/0031-9155/55/22/008 |
| [12] |
International Commission on Radiation Units and Measurements. ICRU Report 36. Microdosimetry[R]. Bethesda: ICRU, 1983.
|
| [13] |
Kase Y, Kanai T, Matsumoto Y, et al. Microdosimetric measurements and estimation of human cell survival for heavy-ion beams[J]. Radiat Res, 2006, 166(4): 629-638. DOI:10.1667/RR0536.1 |
| [14] |
Kiefer J, Straaten H. A model of ion track structure based on classical collision dynamics[J]. Phys Med Biol, 1986, 31(11): 1201-1209. DOI:10.1088/0031-9155/31/11/002 |
| [15] |
Chatterjee A, Schaefer HJ. Microdosimetric structure of heavy ion tracks in tissue[J]. Radiat Environ Biophys, 1976, 13(3): 215-227. DOI:10.1007/BF01330766 |
| [16] |
Furusawa Y, Fukutsu K, Aoki M, et al. Inactivation of aerobic and hypoxic cells from three different cell lines by accelerated 3He-, 12C- and 20Ne-ion beams[J]. Radiat Res, 2000, 154(5): 485-496. DOI:10.1667/RRXX41.1 |
| [17] |
Inaniwa T, Kanematsu N. Adaptation of stochastic microdosimetric kinetic model for charged-particle therapy treatment planning[J]. Phys Med Biol, 2018, 63(9): 095011. DOI:10.1088/1361-6560/aabede |
| [18] |
Sato T, Furusawa Y. Cell survival fraction estimation based on the probability densities of domain and cell nucleus specific energies using improved microdosimetric kinetic models[J]. Radiat Res, 2012, 178(4): 341-356. DOI:10.1667/rr2842.1 |
| [19] |
International Commission on Radiation Units and Measurements. ICRU Report 49. Stopping powers and ranges for protons and alpha particles[R]. Bethesda: ICRU, 1993.
|
| [20] |
International Commission on Radiation Units and Measurements. ICRU Report 73. Stopping of ions heavier than helium[R]. Bethesda: ICRU, 2005.
|
| [21] |
Olko P, Booz J. Energy deposition by protons and alpha particles in spherical sites of nanometer to micrometer diameter[J]. Radiat Environ Biophys, 1990, 29(1): 1-17. DOI:10.1007/BF01211231 |
 2023, Vol. 43
2023, Vol. 43


