直肠癌发病率逐年攀升^[1-2]，调强放疗能在保证足够的靶区剂量覆盖的基础上降低靶区周边组织的受量，有效增加肿瘤的局部控制率，减少远端转移，降低局部复发率^[3-4]，因此是直肠癌治疗的主要手段之一。调强放疗的精确执行有赖于对各类误差的评估和有效控制^[5]。其中，六维摆位误差对放疗计划的剂量学影响一直是放疗重点关注的问题之一。在准确的剂量学评估基础上，可以采用有效的体位固定方式、精确的图像引导和足够的靶区外扩等措施来控制或补偿六维摆位误差带来的剂量学影响。一直以来，大量的研究集中在对平移摆位误差的评估和控制中，而对旋转误差的研究和认识相对较少。一些研究采用CT重采样或者基于锥形束CT(CBCT)变化的方法来研究旋转误差引起的剂量畸变。然而，这些方法所采用的算法引入了不确定性和不一致性，并且难以在临床上应用。为应对这一问题，本研究提出一种基于六维摆位误差引入的调强放疗模拟方法，并应用此方法评估了六维摆位误差对直肠癌调强放疗的剂量学影响。

1.病例选取与参考计划：回顾性选取江苏省肿瘤医院放疗科2021年3月至2022年2月已完成治疗的直肠癌患者21例。年龄51~74岁，中位年龄66岁；采用常规分割的长程放疗手段，分次剂量均为2 Gy，分次次数均为25次。所有病例均无放疗禁忌证。所有病例的治疗计划均通过美国Varian公司Eclipse(15.6)治疗计划设计系统(TPS)设计，并在配有Millennium 120型多叶准直器(MLC)的美国Varian公司TrueBeam医用直线加速器上完成治疗。均采用共面调强放疗(IMRT)技术设计：患者体位均为俯卧位；射野等中心点均近似为计划靶体积(PTV)[临床靶体积(CTV)均匀外扩5 mm]几何中心；6 MV X射线，剂量率600 MU/min；射野个数均为7，机架角度依次为210°、260°、310°、0°、50°、100°和150°；准直器角度均为0°；采用共面照射技术(治疗床角度均为0°)。剂量优化算法为美国瓦里安光子优化(photon optimization, PO)算法；剂量计算算法采用各向异性分析算法(anisotropic analytical algorithm, AAA)，网格设为2.5 mm。归一方式为100%处方剂量覆盖95%的靶区体积。所有计划的各个剂量学指标均满足临床要求。

2.误差分布选择：六维摆位误差SE_6D(x, y, z, θ_x, θ_y, θ_z)由3个平移方向(记为x, y, z)和俯仰、滚动和偏转3个旋转方向(记为θ_x, θ_y, θ_z) 的误差组成。一般来说，同一病例的放疗各个分次的摆位误差相互独立，且服从统一分布。摆位误差分布取决于不同的摆位规范，即体位固定方式和摆位所采用的技术(如CBCT引导的频率和是否采用其他辅助摆位技术等)。本研究将以下两种摆位误差分布纳入研究：

误差分布1：平移方向误差服从均值为0、标准差为4 mm的高斯分布，旋转方向误差服从均值为0°、标准差为2°的高斯分布，即 x, y, z~N(0, 4²), θ_x, θ_y, θ_z~N(0, 2²)。

误差分布2：平移方向误差服从均值为0、标准差为2 mm的高斯分布，旋转方向误差服从均值为0°、标准差为1°的高斯分布，即 x, y, z~N(0, 2²), θ_x, θ_y, θ_z~N(0, 1²)。

3.摆位误差引入与软件开发：加速器坐标系下，六维摆位误差可通过调整6个射野几何参数(等中心三维坐标、机架角度、准直器角度和治疗床角度)来矫正。Yue等^[6]的研究中描述了此变换矩阵；柏朋刚等^[7]采用ArcCheck (Sun Nuclear, 瑞典)验证了此方法的有效性。基于以上研究，可以通过调整射野几何参数来模拟给定的六维摆位误差。在此基础上可以生成模拟治疗中的六维摆位误差并获取相应的剂量分布。

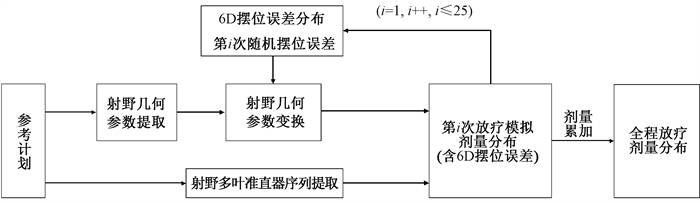
误差引入以及剂量重计算由基于Eclipse(15.6)脚本应用程序接口(Eclipse scripting application programming interface, ESAPI)的自编程序完成^[8]。ESAPI是Eclipse系统自带的一组放疗计划设计工具包，包含了能够实现计划设计中各项功能(如添加调强射野或定义优化条件)的各类函数，可以支持基于C#语言的自定义的计划设计流程的开发。程序包括随机误差生成模块、参数转换模块和各分次模拟计划生成模块，完成6D摆位误差与计划几何参数之间的转换以及各分次误差计划的自动生成。将各个分次的误差仿真计划叠加，即可得到一次完整的全疗程放疗模拟。图 1中给出了基于六维摆位误差引入的治疗模拟软件架构。

图 1 基于六维摆位误差引入的治疗模拟软件架构 Figure 1 Architecture of the treatment simulation software based on six-dimensional setup error

4.剂量学指标：剂量学指标包括靶区剂量覆盖指标、危及器官受量和剂量分布指数。靶区剂量覆盖指标包括CTV的D_98%和D_min。为进一步研究6 D位置误差对靶区各部分剂量覆盖情况的影响，将CTV划分主体靶区(由CTV内收5 mm获得，记为CTV_main)和边缘靶区(CTV抠除CTV_main后获得的壳型结构，命名为CTV_shell)两部分，分别提取CTV_main和CTV_shell的D_98%。另外提取了PTV的D_98%和D_2%。危及器官受量指标包括左右侧股骨头和膀胱的平均剂量D_mean。剂量分布指数包括均匀指数HI、适形指数CI和梯度指数GI。HI定义为：

式中，IA为PTV理想DVH曲线下方面积，AA为PTV实际DVH曲线下方面积，OA为IA和AA重叠区域的面积^[9]。CI定义为100%处方剂量覆盖区域体积与PTV体积的比值。GI定义为50%处方剂量覆盖区域体积与PTV体积的比值，用于衡量靶区外剂量跌落的程度。上述各类指标均由基于ESAPI的自编程序批量提取。

5. 统计学处理：采用scipy.stats统计学软件，模拟治疗中的各个剂量学指标与参考计划的相应指标结果符合正态分布，用x±s表示，两组间比较采用配对t检验。P < 0.05为差异有统计学意义。

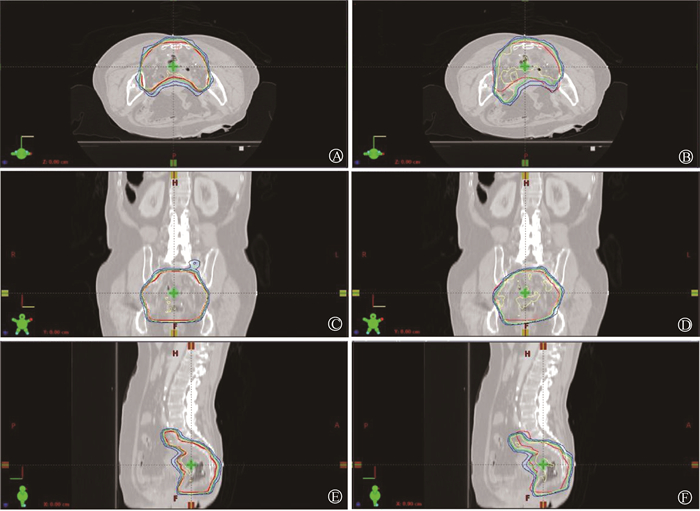
1.旋转摆位误差引入：对于共面调强放疗，平移摆位误差可以通过修改射野等中心值的方式引入到放疗计划中。然而，旋转摆位误差引入的准确性是放疗全程模拟的关键因素。应用本方法对病例#1的参考计划引入(θ_x=10°, θ_y=10°, θ_z=10°)的旋转摆位误差，获取对应的射野几何参数并获取模拟剂量分布。表 1中给出了此次模拟中参考计划和更改后的射野几何参数。图 2中分别给出了理想情况下(参考计划)等中心处3个层面的剂量分布与引入旋转摆位误差(θ_x=10°, θ_y=10°, θ_z=10°)时的剂量分布。可看出各个断面中处方剂量照射区域(黄色处方剂量包绕区域)均发生了偏转。

表 1(Table 1)

表 1 参考计划的射野几何参数和旋转摆位误差(θx=10°, θy=10°, θz=10°)模拟计划的射野几何参数(°) Table 1 Geometrical parameters of the filed for the reference plan and corresponding rotational setup error (θx=10°, θy=10°, θz=10°) simulation plan (°) 射野 参考计划 六维摆位误差模拟 机架 角度 准直器 角度 治疗床 角度 机架 角度 准直器 角度 治疗床 角度 #1 210 0 0 204.6 28.8 323.4 #2 260 0 0 252.3 12.2 346.2 #3 310 0 0 301.2 13.6 357.1 #4 0 0 0 345.9 55.4 44.6 #5 50 0 0 43.2 342.9 337.3 #6 100 0 0 91.8 348.4 350.3 #7 150 0 0 140.4 341.6 4.3

表 1 参考计划的射野几何参数和旋转摆位误差(θx=10°, θy=10°, θz=10°)模拟计划的射野几何参数(°) Table 1 Geometrical parameters of the filed for the reference plan and corresponding rotational setup error (θx=10°, θy=10°, θz=10°) simulation plan (°)

注：红色结构表示PTV 图 2 理想情况下(参考计划)等中心处3个层面的剂量分布与引入旋转摆位误差(θx=10°, θy=10°, θz=10°)时的剂量分布 A.横断面参考剂量分布；B.横断面模拟剂量分布；C.冠状面参考剂量分布；D.冠状面模拟剂量分布；E.矢状面参考剂量分布；F.矢状面模拟剂量分布 Figure 2 Reference and simulated (θx=10°, θy=10°, θz=10°) dose distributions in three planes at the isocenter A.The reference dose distribution in cross section; B. The simulated dose distribution in cross section; C. The reference dose distribution in coronal plane; D. The simulated dose distribution in coronal plane; E. The reference dose distribution in sagittal plane; F. The simulated dose distribution in sagittal plane

2.靶区覆盖：参考计划、误差分布1和分布2下，D_min(CTV)分别为(49.40±0.41)、(47.56±0.76)和(49.17±0.64)Gy。其中，误差分布1情况下，D_min(CTV)相对参考计划的变化为-4.7%(t=-9.91，P < 0.001)，而误差分布2下，D_min(CTV)相对参考计划差异无统计学意义(P=0.23)。图 3中给出了21例直肠癌调强放疗病例中参考计划、误差分布1和分布2的模拟放疗中D_98%(CTV)、D_98%(CTV _ main)和D_98%(CTV _ shell)。参考计划D_98%(CTV)为(50.23±0.07) Gy；误差分布1下，D_98%(CTV)为(49.98±0.10)Gy(t=-8.67，P < 0.001), 有部分病例的D_98%(CTV)低于处方剂量50 Gy；误差分布2下D_98%(CTV)为(50.27±0.09)Gy(t=3.71，P < 0.001)，所有病例的D_98%(CTV)均高于50 Gy。所有病例的主体靶区D_98%(CTV _ main)在两种误差分布下均高于50 Gy，显示在均匀5 mm靶区外扩情况下，主体靶区在两种六维摆位误差存在的情况下均受到足量照射。对于边缘靶区，在两种误差分布情况下，D_98%(CTV_shell)分别由参考计划的(50.22±0.10)Gy变化为(49.88±0.11)Gy(t=-12.46，P < 0.001)和(50.26±0.10) Gy(t=3.53，P < 0.001)。表 2中给出了PTV的D_98%和D_2%在两种误差分布下的变化，可看出由于摆位误差的存在，PTV区域的D_98%均有所下降，误差分布1情况下D_98%的下降程度高于误差分布2。

表 2(Table 2)

表 2 直肠癌患者参考计划、误差分布1和误差分布2的模拟治疗中PTV的靶区覆盖指标(Gy，x±s) Table 2 Target coverages of PTV of the reference plans for rectal cancer IMRT and corresponding simulation plans with setup errors of distribution 1 and 2 in IMRT for rectal cancer (Gy, x±s) 计划 例数 PTV D98% PTV D2% 参考计划 21 49.49±0.07 51.6±0.07 误差分布1 21 46.87±0.24a 51.37±0.26 误差分布2 21 48.61±0.19a 51.5±0.22 注：PTV.计划靶区；a与参考计划比较，t=-48.60、-23.40，P < 0.01

表 2 直肠癌患者参考计划、误差分布1和误差分布2的模拟治疗中PTV的靶区覆盖指标(Gy，x±s) Table 2 Target coverages of PTV of the reference plans for rectal cancer IMRT and corresponding simulation plans with setup errors of distribution 1 and 2 in IMRT for rectal cancer (Gy, x±s)

注：CTV.临床靶区；a与参考计划比较，t=-8.67、3.71、7.66、7.32、-12.46、3.53，P < 0.001 图 3 直肠癌调强放疗病例中参考计划、误差分布1和误差分布2下的模拟放疗中CTV、CTV_main和CTV_shell的靶区覆盖指标 Figure 3 Target coverages of CTV, CTV_main and CTV_shell of the reference plan and corresponding simulation plans with setup errors of distribution 1 and 2 in IMRT for rectal cancer

3.危及器官受量和剂量分布指数：21例直肠癌患者左、右侧股骨头D_mean和膀胱D_mean的参考计划、误差分布1和误差分布2计划差异无统计学意义(P>0.05)。两种摆位误差分布下，HI和GI无明显变化(P>0.05)，CI有不同程度的降低(t=22.36、9.89，P < 0.01)，见表 3。

表 3(Table 3)

表 3 直肠癌患者的参考计划、误差分布1和误差分布2下的模拟放疗中剂量分布指数(x±s) Table 3 Dose distribution of reference plans for rectal cancer IMRT and corresponding simulation plans with setup error of distribution 1 and 2 in IMRT for rectal cancer (x±s) 计划 例数 均匀指数 适形指数 梯度指数 参考计划 21 0.98±0.004 1.45±0.08 4.7±0.68 误差分布1 21 0.98±0.003 1.14±0.04a 4.6±0.66 误差分布2 21 0.98±0.003 1.32±0.08a 4.57±0.63 注：a与参考计划比较，t=22.36、9.89，P < 0.01

表 3 直肠癌患者的参考计划、误差分布1和误差分布2下的模拟放疗中剂量分布指数(x±s) Table 3 Dose distribution of reference plans for rectal cancer IMRT and corresponding simulation plans with setup error of distribution 1 and 2 in IMRT for rectal cancer (x±s)

旋转摆位误差的引入方法的准确性和效率是本研究中放疗全程模拟的关键因素。Nakano等^[10]采用旋转SRS参考计划中GTV结构的方法来模拟旋转摆位误差。Lee等^[11]、Prentou等^[12]和Briscoe等^[13]分别采用旋转参考计划中剂量分布矩阵的方法来模拟旋转摆位误差。然而，上述方法均未对整体的CT空间结构进行旋转，也未重新进行剂量计算。Sagawa等^[14]、Tsujii等^[15]和Isobe等^[16]采用商业化软件MIM (MIM Software, Cleveland, 美国)对参考计划的CT施加旋转，生成模拟CT后重新导入TPS进行剂量计算，以此模拟存在旋转摆位误差时的剂量分布。这种方法的准确度依赖于商业化软件中CT重采样等算法的精度，并且需要CT文件的导入与导出，这些因素可能会限制此方法使用便捷性。本研究通过调整调强计划射野几何参数的方法来引入旋转摆位误差，方法基于较为简单但可靠的变换矩阵。一方面，此方法在TPS中基于ESAPI实现了参考CT影像的“旋转”(相对于射野组)，经过剂量重新计算后直接获取模拟的剂量分布，避免了因引入额外的图像处理算法或参数带来的计算不确定性；另一方面，由于模拟过程无需借助外部软件以及放疗文件的导入/导出，而是采用可以整合入TPS的基于ESAPI开发的工具，这提高了摆位误差模拟的效率和可行性，此方法同样也适用于其他已提供外部接口的商业化TPS，如Pinnacle和RayStation等^[17-18]。

摆位误差分布取决于各个放疗部门所选用的摆位规范和执行力。放疗摆位规范包含多个范畴，如患者体位固定方式^[19]、摆位所采用的技术^[20-21](如激光线+体表标记法、CBCT引导、光学表面引导系统OSMS辅助摆位等)以及使用频率和科室的培训和管理制度等。本研究选取的两种摆位误差的分布是基于上述以往的文献报道，并结合本单位的历史摆位数据和经验综合考虑选取。更明确地说，本研究采用的误差分布1用于模拟激光线+体表标记的摆位方式所带来的摆位误差；而误差分布2则用于模拟基于CBCT的图像引导放疗(CBCT-IGRT)或基于OSMS等设备的光学表面引导放疗(OSMS-SGRT)中的摆位误差。虽然本方法所需预定义的误差分布不仅限于上述两种分布(无论是误差分布的形式还是幅度)，但是结果的有效性依赖于摆位误差数据库的可信度。

Van Herk等^[22-23]基于点靶区的理论研究表明，系统误差能够导致剂量分布相对于靶区发生偏移，而随机误差则会引起剂量分布相对于靶区的模糊效应(blurring effect)。模糊效应指CTV中心处靶点由于位于剂量分布均匀区域内部，随机摆位误差对其造成的剂量影响较小，而CTV边缘点因为接近剂量分布梯度区，随机摆位误差可能会引起这些靶点在某几次治疗中移出剂量均匀区之外，最终导致剂量欠量。然而，从实践的观点来看，模糊效应对放疗的影响程度取决于多种因素，如计划中剂量均匀区的大小和形状(取决于靶区形状、PTV外扩尺寸的大小和方式)、剂量梯度区的陡峭程度(取决于计划设计的方式)和摆位误差的大小(取决于所采用的摆位规范)等。本研究基于临床所用的调强放疗计划、靶区外扩方式和两种给定的误差分布模拟了直肠癌调强放疗，并且将旋转误差的影响考虑在内。本研究表明，在误差较大的摆位规范下(误差分布1)，CTV的D_min相比参考计划下降了4.7%，主体靶区(CTV_main)的D_98%高于参考计划，而边缘靶区(CTV_shell)D_98%则显著降低，并且低于处方剂量。在误差较小的摆位规范下(误差分布2)，CTV的D_min相比参考计划差异无统计学意义，主体靶区和边缘靶区的D_98%均略微高于参考计划以及处方剂量。表明在误差分布2的摆位规范下，5 mm的均匀外扩可以保证直肠癌调强放疗的靶区覆盖；而误差分布1的摆位规范下，5 mm的均匀外扩可能会导致边缘靶区欠量以及剂量冷点。另外，在两种摆位误差存在的情况下，危及器官平均受量无变化或变化甚微。CI有不同程度的削弱，但是变化程度甚微，临床意义有限。本研究的结果与Van Herk等^[23]理论研究中的模糊效应相符合，并给出了具体的剂量学影响。一方面，基于此类模拟可以直观地评估六维摆位误差对给定的一次调强放疗的剂量学影响，并采取相应的措施对治疗进行提前干预(如采用更加严格的摆位规范)；另一方面，本方法也可用于直肠癌放疗中的个性化的外扩选择，如基于多次模拟的非均匀外扩方式的选取，以期在保证靶区剂量覆盖的基础上，降低危及器官受量。

本研究有不足之处。首先，本模拟方法仅考虑了调强放疗各分次的刚性摆位误差，而无法模拟因患者膀胱充盈程度变化以及体型变化引起的内部解剖结构的形变的情况^[24]。其次，本方法基于射野参数变换的方法来引入六维摆位误差，模拟效率与参考计划的射野数目相关，因此只适用于几个或者多个射野的调强放疗计划的全程模拟，对于包含上百个控制点(即上百组射野几何参数)的容积旋转调强放疗(VMAT)计划则可能难以模拟。

基于ESAPI的六维摆位误差引入及治疗模拟软件能够给出模拟治疗后的患者体内的剂量学分布。模拟过程在TPS中完成，不依赖任何外部软件，模拟结果准确并且高效。结果可用于治疗前的剂量学预估，以此基础上可以进一步探索如何选择合理的摆位规范以及靶区外扩方式。

利益冲突  所有作者声明无利益冲突

作者贡献声明  郑佳俊负责数据分析、论文写作；游鸿强参与实验设计和实验结果处理；翟振宇指导实验设计和实验结果分析；何侠、孙丽指导论文写作与修改