2. 中南大学自动化学院, 长沙 410083
2. School of Automation, Central South University, Changsha 410083, China
调强放射治疗(intensity modulated radiation therapy, IMRT)是当前主流放疗技术,计划设计是其关键环节。设计者需要根据临床经验和机构要求,不断调整优化参数,反复优化,直至计划质量满足临床要求,并达到设计者认为的最优状态,此过程称为试错。试错过程耗时耗力,临床工作负荷重,计划质量比较依赖设计者经验,不同设计者的计划质量一致性较差[1-3]。目前,已研发了一些自动计划方法,希望降低临床计划的人力和时间成本,提升计划质量一致性,例如基于先验知识的自动计划(knowledge-based planning, KBP)[1-4]、基于模板的自动计划(protocol-based planning, PBP)[5-6],以及基于多目标优化(multi-criteria optimization planning, MCOP)的自动计划等[7-8]。然而,已有方法大多过于依赖临床经验,存在主观性强、扩展性差等问题[9-10]。同时,目前相关研究多针对肿瘤个体化差异较小的病种,对个体化差异较大病种的研究非常有限。基于此,本研究提出一种新的自动计划方法,利用元启发策略模拟人工计划试错,并探索最优的计划优化参数组合,以期解决上述问题。
资料与方法1. 病例资料:回顾性选择20例肿瘤个体化差异大的病例,进行人工计划和自动计划设计。包括7例脑瘤、7例肺癌和6例肝癌患者。脑瘤计划处方剂量为60 Gy/30次,射野数5~8个,靶区体积范围193.9~566.2 cm3,肿瘤分布为3例偏左、3例偏右、1例居中。肺癌计划处方为54 Gy/30次,射野数5~8个,靶区体积为96.2~280.0 cm3,正常肺体积为1 988.3 ~ 4 533.5 cm3,肿瘤分布为3例偏左、2例偏右、2例居中。肝癌计划处方剂量为45~48 Gy/15次,射野数6~9个,靶区体积为162.6 ~298.3 cm3,正常肝脏体积为676.4 ~1 466.8 cm3。
2. 人工计划设计:为了排除计划系统差异对计划对比的干扰,人工计划和自动计划均基于matRad计划系统,人工计划均由从业5年以上的临床物理师完成。从Eclispe计划系统导出包含CT影像和勾画结果的DICOM文件,导入matRad计划系统,射束中心定在肿瘤质心,所有射野的数量(脑瘤:5~8个,肺癌:5~8个,肝癌:6~9个)和角度与临床治疗计划保持一致,处方剂量参照临床治疗计划。脑瘤处方:靶区60 Gy/30次,脑干Dmax<54 Gy(若贴近靶区,可放宽至V60<1%), 垂体Dmax<60 Gy,视神经与视交叉Dmax<54 Gy(若贴近靶区,可放宽至V60<1%),眼晶状体Dmax<9 Gy;肺癌处方:靶区54 Gy/30次,双肺V20<25%、V5<55%,Dmean<13 Gy, 脊髓Dmax<40 Gy, 食管Dmax < 61 Gy, 心脏V40<30%、V30<40%;肝癌处方:靶区45~48 Gy/15次,肝脏Dmean<21 Gy,胃Dmax<50 Gy,肾脏Dmean<20 Gy,脊髓Dmax<40 Gy。归一方式为95%的靶区体积覆盖100%的处方剂量。计划设计者设置初始的优化条件,进入人工试错流程,直至满足临床处方要求,且达到设计者认为的最优计划。剂量计算体素分辨率为3.0 mm × 3.0 mm × 3.0 mm。
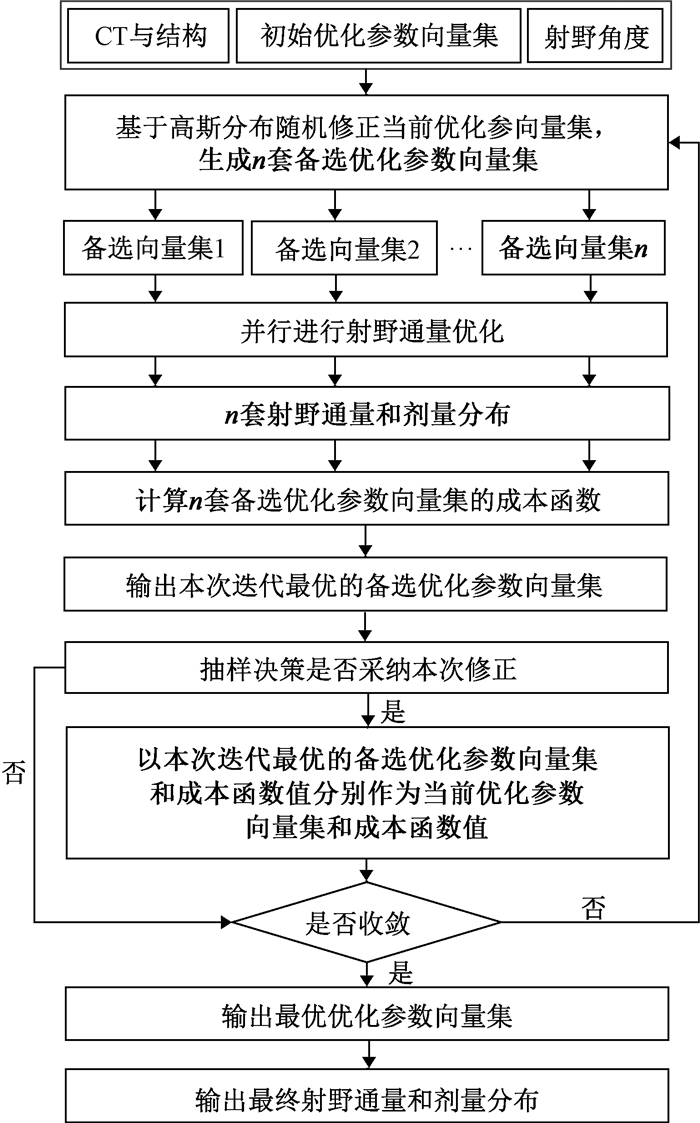
3. 基于并行模拟退火试错的自动计划:元启发策略属于数学优化领域,适用于信息受限的或昂贵的优化问题,以随机优化的方式探索这类问题的可行优化空间,根据历史结果引导探索过程,逐步找到最优或近似最优解,在不同问题之间具有较好的扩展性能。常见的元启发算法包括禁忌搜索、模拟退火及遗传算法等[11-12]。具体到放疗计划设计问题,计划设计者利用自身临床经验进行优化参数调整,本质上是基于启发策略的优化参数试错过程。为了兼顾计划优化参数自动调整的局部搜索和全局探索能力,本研究提出了基于元启发策略的肿瘤调强放疗自动计划方法,设计了基于并行模拟退火试错的自动计划(AuTomatic Planning based on parallel SimulaTed Annealing trial and eRror, ATP-STAR)流程,该方法包括两个部分:基于高斯卷积修正优化参数和基于模拟退火选择备选优化参数向量集。
图 1为ATP-STAR方法流程。本研究基于matRad开源治疗计划系统平台(2.10.1版)[13],使用python语言(3.7.9)开发图 1自动计划流程。matRad系统中剂量计算使用奇异值分解笔形束算法,射野通量优化使用Matlab中IPOPT(interior-point optimization)代码包,基于梯度信息进行优化,详见matRad相关文献[13]。自动计划的剂量计算分辨率、射野数量和角度、处方剂量和归一方式均与人工计划一致。本研究所用计算工作站的主要硬件配置:CPU为AMD ThreadRipper 3970X,显卡NVIDIA GeForce RTX 3090,内存196 Gb。
|
图 1 基于并行模拟退火试错的自动计划(ATP-STAR)流程图 Figure 1 Flowchart of automatic treatment planning based on trial and error using parallel simulated annealing (ATP-STAR) |
(1) 自动计划的成本函数构建:获取计划试错需要的初始信息,包括射野角度、CT、结构以及初始优化参数等。计划设计者设置初始的优化参数,进行单次射野通量优化,计算危及器官的初始平均剂量,d(int)OAR。采用Mayo等[14]设计的基于优先级加权的泛化评估方式构建自动计划优化成本函数:
| $ L_{\mathrm{opt}}=\frac{\sum_{j=1}^{N_D}\left(2^{-t_j+1} \cdot D_j\right)}{\sum_{j=1}^{N_D} 2^{-t_j+1}} $ | (1) |
式中,Lopt为优化成本函数,ND为待评估剂量学指标的个数,tj为第j个剂量学指标Dj的权重系数参数,根据不同结构的临床重要性,脑瘤剂量学指标的权重系数参数tj(适形指数CI,均匀性指数HI,脑干, 晶状体, 视神经, 视交叉, 垂体, 环)取(0, 1, 2, 2, 3, 3, 3, 4),肺癌剂量学指标的权重系数参数tj(CI, HI, 脊髓, 肺, 心脏, 环)取(0, 1, 2, 2, 3, 4),肝癌剂量学指标的权重系数参数tj(CI, HI, 脊髓, 肝脏, 肾脏, 胃, 环)取(0, 1, 2, 2, 3, 3, 4),Dj包括靶区的均匀性指标DHI、靶区的适形性指标DCI和各个危及器官剂量指标DOAR,分别使用公式(2)~(4)计算[15]:
| $ D_{\mathrm{HI}}=\min \left(1, \quad \max \left(\frac{\mathrm{HI}-\mathrm{HI}^{-}}{\mathrm{HI}^{+}-\mathrm{HI}^{-}}, 0\right)\right) $ | (2) |
| $ D_{\mathrm{CI}}=\min \left(1, \quad \max \left(\frac{\mathrm{CI}^{+}-\mathrm{CI}}{\mathrm{CI}^{+}-\mathrm{CI}^{-}}, 0\right)\right) $ | (3) |
| $ D_{\mathrm{OAR}}=\min \left(1, \quad \max \left(\frac{\bar{d}_{\mathrm{OAR}}-\bar{d}_{\mathrm{OAR}}^{-}}{\bar{d}_{\mathrm{OAR}}^{+}-\bar{d}_{\mathrm{OAR}}^{-}}, \quad 0\right)\right) $ | (4) |
式中,HI为靶区均匀性数值,HI+和HI-分别为预设的均匀性上下限,HI使用公式(5)计算,HI+和HI-分别取8.0和3.0;CI为靶区适形性数值,CI+和CI-分别为预设的适形性上下限,CI使用公式(6)计算,CI+和CI-分别取0.95和0.65;dOAR为某个危及器官的平均剂量,dOAR+和dOAR-分别为对应危及器官平均剂量的预设上下限,分别取1.1倍和0.9倍的初始平均剂量,dOAR(int)。
| $ \mathrm{HI}=\frac{D_5-D_{95}}{D_p} \times 100 $ | (5) |
| $ \mathrm{CI}=\frac{\left(T V_{95}\right)^2}{T V \times V_{95}} $ | (6) |
式中,D5和D95分别为5%和95%的靶区体积所达到的最大剂量;Dp为靶区处方剂量;TV95为靶区内达到95%处方剂量的体积;TV为靶区体积;V95为达到95%处方剂量的体积,包括靶区内外。
(2) 优化参数的自动调整
① 基于高斯卷积修正优化参数。对初始的优化参数(包括剂量参数、体积参数和权重参数)进行向量化编码,获得初始的优化参数向量集合(简称向量集),包括剂量优化参数向量、体积优化参数向量和权重优化参数向量。剂量优化参数向量仅包含所有串行器官的剂量优化参数,体积优化参数向量仅包含所有并行器官的体积优化参数,权重优化参数向量包含所有靶区和危及器官的权重优化参数。在每次迭代中,基于高斯分布随机修正当前的优化参数向量集,获得n套备选优化参数向量集,本研究n取10。设计了公式(7)修正不同的优化参数向量。
| $ {\mathop p\limits^{\rightharpoonup}} _{{\rm{opt}}}^\prime = \left| {{{{\mathop p\limits^{\rightharpoonup}}}_{{\rm{opt}}}} + \alpha \cdot {{{\mathop r\limits^{\rightharpoonup}}}_n} \cdot {{{\mathop p\limits^{\rightharpoonup}}}_{{\rm{opt}}}}} \right| $ | (7) |
式中,
② 基于模拟退火选择备选优化参数向量集。并行进行n套备选优化参数向量集的射野通量优化。根据公式(1)分别计算这n套备选优化参数向量集对应的优化成本函数,输出本次迭代内最优的备选优化参数向量集。设计了公式(8)计算本次修正的接受概率p(Ltot, L′tot),若采纳本次修正,以本次迭代最优的备选优化参数向量集和成本函数值分别作为当前优化参数向量集和最优成本函数值。
| $ P\left(L_{\text {tot }}, L_{\text {tot }}^{\prime}\right)= \begin{cases}1.0, & L_{\text {tot }}^{\prime} \leqslant L_{\text {tot }} \\ \exp \left(\frac{L_{\text {tot }}-L_{\text {tot }}^{\prime}}{\beta \cdot \exp (-\gamma \cdot k)}\right), & L_{\text {tot }}^{\prime}>L_{\text {tot }}\end{cases} $ | (8) |
式中,L′tot和Ltot分别为本次迭代最优备选优化参数向量的成本函数值和当前成本函数值;β为初始温度参数,多次随机修正优化参数向量集,计算随机抽样过程中成本函数的标准差,以标准差作为初始温度参数,本研究选0.03;γ为衰减因子参数,根据实验经验选0.07,k为迭代次数。
判断优化是否收敛或达到预设的最大迭代次数。若是则输出最终的优化参数向量集,并输出最终射野通量和剂量分布,否则返回随机修正步骤,重新获取备选优化参数向量集。
4. 统计学处理:采用SPSS22.0软件,统计方法采用威尔科克森符号秩(Wilcoxon signed-rank)非参数检验,符合正态分布数据用x±s表示。P < 0.05为差异有统计学意义。
结果1.剂量学指标对比:表 1为脑瘤ATP-STAR与人工计划的剂量学参数比较。ATP-STAR靶区均匀性均优于人工计划,差异有统计学意义(z=2.28,P=0.022)。ATP-STAR脑干Dmax和Dmean、右晶状体Dmax与人工计划的差异无统计学意义(P>0.05)。对于其余危及器官,ATP-STAR均优于人工计划,其中,左晶状体Dmean、左视神经Dmean、右视神经Dmax、垂体Dmean和Dmax、靶区周围正常组织Dmean以及全身累积剂量Dmean的差异具有统计学意义(z=2.10~2.29, P < 0.05)。
|
|
表 1 脑瘤ATP-STAR与人工计划剂量学参数比较(x±s) Table 1 Comparison of dosimetric parameters between ATP-STAR and manual plans for brain tumors(x±s) |
表 2为肺癌ATP-STAR与人工计划的剂量学参数比较。ATP-STAR靶区均匀性优于人工计划,差异统计学意义(z=2.29, P=0.022),适形性略差于人工计划,差异有统计学意义(z=2.29, P=0.022)。ATP-STAR所有危及器官的剂量学指标均优于人工计划,差异有统计学意义(Z=2.12~2.30,P=0.05)。
|
|
表 2 肺癌ATP-STAR与人工计划剂量学参数比较(x±s) Table 2 Comparison of dosimetric parameters between ATP-STAR and manual plans for lung cancer(x±s) |
表 3为肝癌ATP-STAR与人工计划的剂量学参数比较。ATP-STAR靶区均匀性优于人工计划,差异有统计学意义(z=2.11,P=0.035),适形性与人工计划差异无统计学意义(P>0.05)。ATP-STAR所有靶区的剂量学指标均优于人工计划,脊髓Dmax和Dmean、肝脏Dmean、肾脏Dmean、靶区周围正常组织Dmean以及全身累积剂量Dmean的差异有统计学意义(z=2.10~2.11, P < 0.05)。
|
|
表 3 肝癌ATP-STAR与人工计划剂量学参数比较(x±s) Table 3 Comparison of dosimetric parameters between ATP-STAR and manual plans for liver cancer(x±s) |
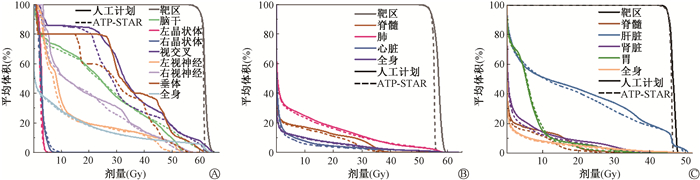
2. DVH结果对比: 图 2为人工计划与自动计划的DVH曲线对比。可以看出,自动计划靶区的DVH曲线更加陡峭,均匀性更好。自动计划多数关键危及器官的DVH曲线位于人工计划之下,对危及器官保护更好。
|
图 2 不同肿瘤放疗计划的DVH图 A.脑瘤;B.肺癌;C.肝癌 Figure 2 Dose-volume histograms (DVHs) of different radiotherapy plans A. Brain tumor; B. Lung cancer; C. Liver cancer |
3. 计划设计时间对比: 总体而言,ATP-STAR自动计划与人工计划所用时间两者耗时接近,脑瘤ATP-STAR: (83.4±42.9) min, 人工计划:(90.3± 33.3) min, 肺癌ATP-STAR: (157.8±34.8) min,人工计划:(150.2±41.1) min,肝癌ATP-STAR: (134.7±24.9) min, 人工计划:(139.9±17.3) min,差异均无统计学意义(P>0.05)。
讨论本研究提出了一种新的肿瘤调强放疗自动计划方法,即ATP-STAR,基于并行模拟退火算法模拟人工计划试错,利用元启发策略,并行探索最优的计划优化参数组合,能够实现肿瘤个体化差异较大病种(如脑瘤、肺癌和肝癌)的自动计划设计。所提出的ATP-STAR自动计划方法较少依赖人工经验,易于推广,能改善调强放疗计划质量及一致性,并节省临床人力和时间成本。
ATP-STAR方法能够减小不同医疗机构、不同设计者之间的计划质量差异,并改善计划质量。ATP-STAR仅需预设优化所需初始信息,即可一键启动,进行自动试错,中间无需使用不同机构或设计者的临床经验进行人工干预,故而能够减轻不同机构及计划设计者之间的计划质量差异。本研究使用肿瘤个体化差异较大的病种作为测试病种,证明了自动计划的多数关键剂量学参数优于人工计划,且差异具有统计学意义。ATP-STAR方法采用并行优化策略,既可提高优化效率,又能充分探索优化参数空间。每次迭代随机生成10套备选优化参数向量集进行并行优化,若行20次迭代,实则完成200次试错,远高于临床人工计划的试错次数(通常为十几次至几十次不等),对优化参数空间的探索更为充分,计划质量故而更好。
尽管KBP或PBP自动计划方法同样被证明可以提高计划质量的一致性,并减轻临床工作负荷,但它们产生计划的质量依赖于所建立的数据库质量或模板质量。同时,考虑到不同肿瘤部位的解剖特点不同,不同医疗机构的治疗规范不同,不同设计者的临床经验和习惯不同,为了保证自动计划的质量,需对不同肿瘤部位、临床机构及设计者建立不同的数据库或模板,这可能会限制这些方法的扩展能力。MCOP方法需要计划设计者在帕累托最优计划集中权衡选择最终计划,当优化参数较多时,帕累托最优计划集较大,会给设计者的选择造成困扰。
上述不足之处导致多数已有自动计划方法适用于肿瘤个体化差异较小的病种,例如鼻咽癌[16-18]、前列腺癌[19-20]、宫颈癌[21-22]、直肠癌[23-24]等,难以扩展至个体化差异大的病种,本研究ATP-STAR方法的验证对象为肿瘤个体化差异较大的病种(脑瘤、肺癌和肝癌),这些肿瘤的大小、形状和位置变化较大,不同病例间优化参数差异更大,自动计划任务更具挑战性,证明了ATP-STAR方法的扩展能力。Zhang等[25]设计了一种面向肺癌的自动计划方法,计划质量优于人工计划,但其自动试错过程是逐个对优化参数进行调试,并非同步优化所有的优化参数,对优化参数组合空间探索可能不充分。Kroshko等[26]提出了一种基于贝叶斯随机前沿分析的肺癌立体定向放疗自动计划方法,使用几何特征预测计划的剂量体积直方图指标;Barragán-Montero等[27]提出了一种适用于肺癌的计划剂量分布预测方法,将适形计划的剂量分布作为额外信息输入深度学习模型,提升了模型预测准确度;然而,上述两种肺癌自动计划方法需要建立历史计划数据库,过于依赖先验人工经验,缺少将预测剂量分布转化为临床可执行计划的有效方法。
最近,有研究机构设计了不同的自动修正计划优化参数的方法,用于模拟人工试错过程,减轻自动计划对先验临床经验的依赖性。例如,Huang等[15]基于Nelder-Mead单纯形法调整优化参数,模拟人工试错,使用了6例头颈和21例前列腺癌病例进行验证,证明该方法能够实现自动试错,并降低主要危及器官的剂量。优化参数包括剂量优化参数、体积优化参数和权重优化参数,人工试错需要对三者均进行试错,缺一不可。Nelder-Mead单纯形法需要在优化过程中产生具备n+1个顶点(n为待优化变量个数)的初始单纯形,在n过大时,由于硬件和效率限制,Nelder-Mead单纯形法方法不再适用[28-29]。Huang等[15]忽略了剂量和体积优化参数的试错,可能会限制该方法的扩展能力。Maass等[30]设计了另外两种优化参数修正方法模拟人工计划试错,分别为均匀随机抽样和贝叶斯优化,并收集了10例肺癌立体定向放疗病例进行测试,证明这两种修正方法均可以实现自动试错,贝叶斯优化方法的计划质量优于均匀随机抽样。尽管基于贝叶斯优化的优化参数修正方法展现了较好的效果,但贝叶斯优化的优化参数有限,一般为10~20个,更适合低维优化参数空间的调试。本研究采用ATP-STAR方法,使用高斯卷积修正优化参数,对所有优化参数(包括剂量参数、体积参数和权重参数)进行向量化编码,不存在优化参数个数限制。而且,采用模拟退火选择每次迭代的备选优化参数向量集,利用其随机游走特性,扩大对优化参数空间的探索范围。
本研究工作存在一些局限性。首先,虽然总病例数有20例,但每个病种的病例数量少(脑瘤和肺癌各7例,肝癌6例),可能会影响统计结果的精确性;其次,本研究基于matRad开源治疗计划系统平台开展,未验证与临床常用计划系统的兼容性。此研究是关于ATP-STAR方法的先期验证研究,期望在未来的研究中,纳入更多肿瘤部位及病例,并利用商用治疗计划系统的脚本功能,进一步验证该方法的临床适用性,正如Maass等[30]的工作使用了RayStation计划系统完成。同时,期望在未来的研究中,将ATP-STAR方法扩展至容积旋转调强(VMAT)的自动计划,但考虑到VMAT单次优化时间过长,如何减少单次优化时长是成功扩展的关键,基于GPU加速的优化技术可能是一种潜在的解决方案,需要在日后的工作中进一步验证。
利益冲突 所有作者声明不存在利益冲突
作者贡献声明 杨晓喻负责实验设计、论文撰写;赵于前、杨振负责技术指导及论文修改;李书舟、邵其刚参与研究;曹瑛负责研究路线设计、论文修改
| [1] |
Momin S, Fu Y, Lei Y, et al. Knowledge-based radiation treatment planning: A data-driven method survey[J]. J Appl Clin Med Phys, 2021, 22(8): 16-44. DOI:10.1002/acm2.13337 |
| [2] |
Wu B, Kusters M, Kunze-Busch M, et al. Cross-institutional knowledge-based planning (KBP) implementation and its performance comparison to auto-planning engine (APE)[J]. Radiother Oncol, 2017, 123(1): 57-62. DOI:10.1016/j.radonc.2017.01.012 |
| [3] |
范嘉伟, 王佳舟, 胡伟刚. 调强放射治疗自动计划技术的研究进展[J]. 中国癌症杂志, 2018, 28(6): 435-438. Fan JW, Wang JZ, Hu WG. Automatic planning technique in intensity-modulated radiation therapy[J]. China Oncol, 2018, 28(6): 435-438. DOI:10.19401/j.cnki.1007-3639.2018.06.007 |
| [4] |
Ge Y, Wu QJ. Knowledge-based planning for intensity-modulated radiation therapy: A review of data-driven approaches[J]. Med Phys, 2019, 46(6): 2760-2775. DOI:10.1002/mp.13526 |
| [5] |
Vanderstraeten B, Goddeeris B, Vandecasteele K, et al. Automated instead of manual treatment planning? A plan comparison based on dose-volume statistics and clinical preference[J]. Int J Radiat Oncol Biol Phys, 2018, 102(2): 443-450. DOI:10.1016/j.ijrobp.2018.05.063 |
| [6] |
Hansen CR, Bertelsen A, Hazell I, et al. Automatic treatment planning improves the clinical quality of head and neck cancer treatment plans[J]. Clin Transl Radiat Oncol, 2016, 1: 2-8. DOI:10.1016/j.ctro.2016.08.001 |
| [7] |
Thieke C, Küfer K-H, Monz M, et al. A new concept for interactive radiotherapy planning with multicriteria optimization: first clinical evaluation[J]. Radiother Oncol, 2007, 85(2): 292-298. DOI:10.1016/j.radonc.2007.06.020 |
| [8] |
Monz M, Küfer KH, Bortfeld TR, et al. Pareto navigation-algorithmic foundation of interactive multi-criteria IMRT planning[J]. Phys Med Biol, 2008, 53(4): 985-998. DOI:10.1088/0031-9155/53/4/011 |
| [9] |
Hussein M, Heijmen B, Verellen D, et al. Automation in intensity modulated radiotherapy treatment planning-a review of recent innovations[J]. Br J Radiol, 2018, 91(1092): 20180270. DOI:10.1259/bjr.20180270 |
| [10] |
Zhang Q, Zhang S, Wang M, et al. Research progress on automatic treatment planning methods for radiotherapy[J]. Chin J Radiat Oncol, 2021, 30(3): 316-320. DOI:10.3760/cma.j.cn113030-20191202-00497 |
| [11] |
Blum C, Roli A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison[J]. ACM Comput Surv, 2003, 35(3): 268-308. DOI:10.1145/937503.937505 |
| [12] |
Bianchi L, Dorigo M, Gambardella LM, et al. A survey on metaheuristics for stochastic combinatorial optimization[J]. Nat Comput, 2009, 8(2): 239-287. DOI:10.1007/s11047-008-9098-4 |
| [13] |
Wieser HP, Cisternas E, Wahl N, et al. Development of the open-source dose calculation and optimization toolkit matRad[J]. Med Phys, 2017, 44(6): 2556-2568. DOI:10.1002/mp.12251 |
| [14] |
Mayo CS, Yao J, Eisbruch A, et al. Incorporating big data into treatment plan evaluation: development of statistical DVH metrics and visualization dashboards[J]. Adv Radiat Oncol, 2017, 2(3): 503-514. DOI:10.1016/j.adro.2017.04.005 |
| [15] |
Huang C, Nomura Y, Yang Y, et al. Meta-optimization for fully automated radiation therapy treatment planning[J]. Phys Med Biol, 2022, 67(5): 055011. DOI:10.1088/1361-6560/ac5672 |
| [16] |
Bai P, Weng X, Quan K, et al. A knowledge-based intensity-modulated radiation therapy treatment planning technique for locally advanced nasopharyngeal carcinoma radiotherapy[J]. Radiat Oncol, 2020, 15(1): 188. DOI:10.1186/s13014-020-01626-z |
| [17] |
Chen X, Men K, Zhu J, et al. DVHnet: a deep learning-based prediction of patient-specific dose volume histograms for radiotherapy planning[J]. Med Phys, 2021, 48(6): 2705-2713. DOI:10.1002/mp.14758 |
| [18] |
Hu J, Liu B, Xie W, et al. Quantitative comparison of knowledge-based and manual intensity modulated radiation therapy planning for nasopharyngeal carcinoma[J]. Front Oncol, 2021, 10: 551763. DOI:10.3389/fonc.2020.551763 |
| [19] |
Sheng Y, Li T, Zhang Y, et al. Atlas-guided prostate intensity modulated radiation therapy (IMRT) planning[J]. Phys Med Biol, 2015, 60(18): 7277-7291. DOI:10.1088/0031-9155/60/18/7277 |
| [20] |
Good D, Lo J, Lee WR, et al. A knowledge-based approach to improving and homogenizing intensity modulated radiation therapy planning quality among treatment centers: an example application to prostate cancer planning[J]. Int J Radiat Oncol Biol Phys, 2013, 87(1): 176-181. DOI:10.1016/j.ijrobp.2013.03.015 |
| [21] |
Yuan Z, Wang Y, Hu P, et al. Accelerate treatment planning process using deep learning generated fluence maps for cervical cancer radiation therapy[J]. Med Phys, 2022, 49(4): 2631-2641. DOI:10.1002/mp.15530 |
| [22] |
Song Y, Hu J, Liu Y, et al. Dose prediction using a deep neural network for accelerated planning of rectal cancer radiotherapy[J]. Radiother Oncol, 2020, 149: 111-116. DOI:10.1016/j.radonc.2020.05.005 |
| [23] |
Zhou J, Peng Z, Song Y, et al. A method of using deep learning to predict three-dimensional dose distributions for intensity-modulated radiotherapy of rectal cancer[J]. J Appl Clin Med Phys, 2020, 21(5): 26-37. DOI:10.1002/acm2.12849 |
| [24] |
Peng J, Chen Y, Zhao J, et al. An atlas-guided automatic planning approach for rectal cancer intensity-modulated radiotherapy[J]. Phys Med Biol, 2021, 66(15): 155011. DOI:10.1088/1361-6560/ac127d |
| [25] |
Zhang X, Li X, Quan EM, et al. A methodology for automatic intensity-modulated radiation treatment planning for lung cancer[J]. Phys Med Biol, 2011, 56(13): 3873-3893. DOI:10.1088/0031-9155/56/13/009 |
| [26] |
Kroshko A, Morin O, Archambault L. Knowledge-based planning algorithm for lung SBRT with robust Bayesian stochastic frontier analysis and missing data management[J]. Med Phys, 2022, 49(10): 6293-6302. DOI:10.1002/mp.15922 |
| [27] |
Barragán-Montero AM, Nguyen D, Lu W, et al. Three-dimensional dose prediction for lung IMRT patients with deep neural networks: robust learning from heterogeneous beam configurations[J]. Med Phys, 2019, 46(8): 3679-3691. DOI:10.1002/mp.13597 |
| [28] |
Nelder JA, Mead R. A simplex method for function minimization[J]. Comput J, 1965, 7(4): 308-313. DOI:10.1093/comjnl/7.4.308 |
| [29] |
Kolda TG, Lewis RM, Torczon V. Optimization by direct search: new perspectives on some classical and modern methods[J]. SIAM Rev, 2003, 45(3): 385-482. DOI:10.1137/S003614450242889 |
| [30] |
Maass K, Aravkin A, Kim M. A hyperparameter-tuning approach to automated inverse planning[J]. Med Phys, 2022, 49(5): 3405-3415. DOI:10.1002/mp.15557 |
 2023, Vol. 43
2023, Vol. 43


