2. 中国计量科学研究院,北京 100029
2. National Institute of Metrology, Beijing 100029, China
192Ir源的比活度较高,易于制作成较小尺寸,已经逐渐取代137Cs、60Co成为医院中最常见的近距离治疗放射源,通常用于宫颈癌[1]和前列腺癌[2]的治疗。目前,国内年消耗192Ir源已超过千颗,因此192Ir近距离治疗源对剂量的精确测量和量值溯源变得迫切。在利用石墨空腔电离室对192Ir γ射线的参考空气比释动能率绝对测量中,室壁修正是绝对测量过程中最大的修正项,室壁修正的准确测量程度直接关系到参考空气比释动能率绝对测量的精确度。RI(I)-K8比对工作的完成对高剂量率192Ir放射源的参考空气比释动能率量值复现[3]与参加国际比对打下了基础。
材料与方法1. 实验装置:采用北京原子高科技术有限公司生产的医用192Ir源作为辐射源。中国计量科学研究院(National Institute of Metrology,NIM)设计并自制了用于192Ir放射源参考空气比释动能率量值复现的球形石墨空腔电离室,如图 1。所设计的石墨空腔电离室壁壳、收集极等部位均选用密度为1.85 g/cm3高纯石墨材料。利用高精度三坐标测量仪测算精度,精度可达到0.001 mm,加工装配后的石墨空腔电离室的体积为102.474 cm3,内径为57.996 mm,壁厚为3.028 mm,收集极长度和直径分别为44.93和2 mm。

|
图 1 石墨空腔电离室示意图 Figure 1 Schematic diagram of graphite cavity ionization chamber |
2. 参考空气比释动能率量值复现原理:根据国际辐射单位与测量委员会(ICRU)90号报告[4]中推荐的参考空气比释动能率
| $ \dot{K}_{\mathrm{R}}=\dot{K}_{\text {air }}(d) \cdot\left(\frac{d}{d_{\text {ref }}}\right)^2 $ | (1) |
| $ \dot{K}_{\text {air }}=\frac{1}{\rho V} \frac{W}{e} \frac{1}{1-g}\left(\frac{\mu_{\mathrm{en}}}{\rho}\right)_{\mathrm{gr}}^{\text {air }}\left(\frac{s}{\rho}\right)_{\text {air }}^{\mathrm{gr}} I k_{\mathrm{i}} $ | (2) |
式中,I为电离室测得的电离电流,pA;ρ为空气密度,g/cm3;V为电离室体积,cm3;
| $ I I k_{\mathrm{i}}=k_{\mathrm{wall}} \cdot k_{\mathrm{stem}} \cdot k_{\mathrm{s}} \cdot k_{\mathrm{an}} \cdot k_{\mathrm{ar}} \cdot k_{\mathrm{pol}} \cdot k_{\mathrm{h}} $ | (3) |
式中,kwall为电离室的室壁修正;kstem为电离室杆散射修正;ks为复合损失修正;kan为轴向不均匀修正;kar为径向不均匀修正;kpol为极性电压修正;kh为空气湿度修正。
3. 室壁修正系数:高能光子穿过电离室壁进入电离腔,室壁对高能光子产生衰减效应,导致一部分的高能光子被室壁吸收,此外,由于电离室壁散射也可能会对电离电流产生影响,因此需要进行修正,这就引入了室壁修正系数kwall[6]。
电离室的室壁修正因子kwall可以分解为壁衰减修正因子katt和壁散射修正因子ksc两部分,计算公式如下:
| $ k_{\text {wall }}=k_{\mathrm{att}} \cdot k_{\mathrm{sc}} $ | (4) |
| $ {k_{{\rm{att}}}} = \frac{{\sum\nolimits_{\rm{i}} {{E_{{\rm{i}}, 0}} \times {e^{{u_{\rm{i}}}{s_{\rm{i}}}}}} }}{{\sum\nolimits_{\rm{i}} {{E_{{\rm{i}}, 0}}} }} $ | (5) |
| $ k_{\mathrm{sc}}=\frac{\sum_{\mathrm{i}} E_{\mathrm{i}, 0}}{R_{\mathrm{tot}}}=\frac{\sum_{\mathrm{i}} E_{\mathrm{i}, 0}}{\sum_{\mathrm{i}}\left(E_{\mathrm{i}, 0}+E_{\mathrm{i}, 1}\right)} $ | (6) |
式中,Ei, 0为第i个初级光子直接相互作用所产生的全部电子的能量沉积;ui为线性衰减系数;si为室壁到相互作用点的路径长度;Ei, 1为第i个初级光子散射发生作用所产生的电子的能量沉积;Rtot为空腔中总的能量沉积[7]。
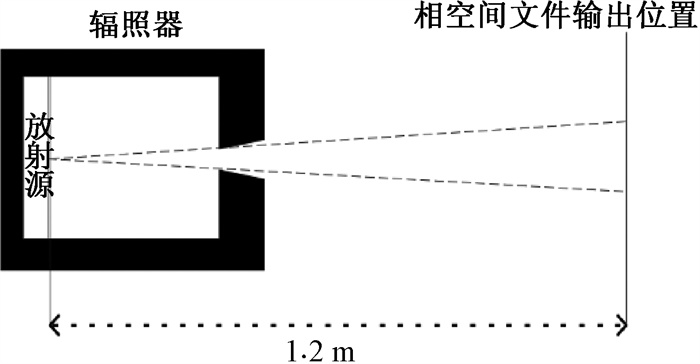
4. 模拟方法:选用最新的EGSnrc版本[8],利用Beamnrc子程序建立192Ir放射源精细结构模型,放射源模型放入辐照器中,如图 2所示(图中放射源的位置按照真实放射源位置);放射源密封于焊接在不锈钢丝绳源辫上的不锈钢源包壳(06Cr19Ni10,密度为7.93 g/cm3)中,有效铱源呈圆柱状,其有效活性长度为3.5 mm,直径0.6 mm,被长6.5 mm,直径1.1 mm的不锈钢壳包裹。结构尺寸和材料组成由原子高科股份有限公司提供。192Ir源的能谱为“ Ir-192_bare_spectrum ”能谱。光子截止能量为0.01 MeV,电子截止能量为0.521 keV,计算了经过放射源包壳和辐照器模型的光子光谱,如图 3所示。
|
图 2 辐照器模型示意图 Figure 2 Schematic diagram of the irradiator model |

|
图 3 距离放射源中心1.2 m处的能谱图 Figure 3 Energy spectrum at a distance of 1.2 m from the center of the radioactive source |
利用CAVSPHnrc子程序,建立球形石墨空腔电离室模型,由两个同心球组成,忽略中心电极,则由外到内有3个区域,分别为空气(1.205×10-3g/cm3)、石墨壁(1.85 g/cm3)和空腔;放射源中心与电离室中心的距离为120 cm,放射源可看做点源[9]。入射能量为经过包壳和辐照器后的能谱,光子截止能量为0.01 MeV,电子截止能量为0.521 keV。计算过程考虑光电效应、康普顿散射和瑞利散射等过程,粒子个数设为1×108。计算出室壁修正kwall。
同时,进一步研究了光子能量、壁厚和不同内径对kwall的影响。根据文献,对影响室壁修正系数kwall的光子能量、壁厚和不同内径电离室进行了蒙特卡罗模拟[10]。计算不同壁厚、不同内径的球形石墨空腔电离室0.02~1.3 MeV的单能光子照射条件下的kwall变化。
结果1.192Ir基准石墨空腔电离室室壁修正系数kwall的验证:利用蒙特卡罗软件EGSnrc对美国国家标准技术研究院(National Institute of Standards and Technology,NIST)的50 cm3的球形石墨空腔电离室和英国国家物理标准研究院(National Physical Laboratory,NPL)的100 cm3的球形石墨空腔电离室进行了模拟,NPL、NIST和NIM电离室的基本尺寸如表 1所示。
|
|
表 1 不同研究机构电离室基本尺寸 Table 1 Basic dimensions of ionization chambers in different research institutions |
结果表明,中国计量院对NPL石墨空腔电离室室壁修正系数的结果与NPL的模拟结果[10]具有较好的一致性,与NIST模拟结果[11]的相对偏差为0.41%。基于EGSnrc蒙特卡罗模拟软件,建立了放射源精细几何结构模型、辐照器模型和球形石墨空腔电离室模型,利用Beamnrc子程序和CAVSPHnrc子程序计算了经过放射源包壳和辐照器模型的光子光谱和球形石墨空腔电离室的室壁修正。球形石墨空腔电离室的室壁修正不确定度为0.031%。
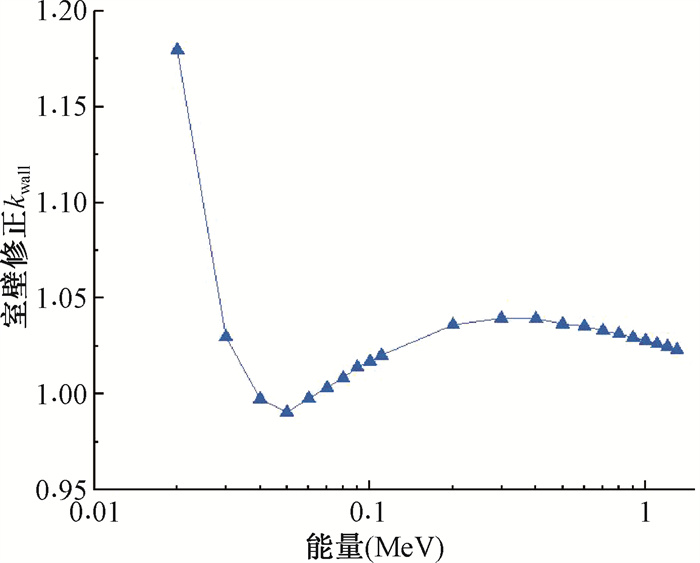
2. 对自制的球形石墨空腔电离室进行了在不同光子能量下的室壁修正系数kwall模拟,模拟结果如图 4所示。可以看到曲线先下降,在缓慢上升最后趋于平缓,在0.02~0.03 MeV能量范围内室壁材料对光子的衰减和散射份额相对较大,且散射衰减份额低于衰减份额,因此,在此能量段kwall>1,在0.03~0.06 MeV范围内kwall值散射份额高于衰减份额,因此导致此能量段kwall < 1,并且在0.05 MeV附近kwall达到最低,参考NIST数据库中光子在石墨中的质量能量吸收系数最小,在此能量下光子转移给石墨的能量较少,从而散射份额较高,导致壁修正随能量变化的曲线在此出现谷底。当光子能量超过0.06 MeV时,散射与衰减的份额随着能量的变化均呈现变小的趋势,且变化率也越来越小,但始终衰减份额高于散射份额,表明了石墨空腔电离室在能量较高的射线下壁修正较低,可以得到较好的能量响应。
|
图 4 192Ir基准电离室kwall随能量变化 Figure 4 Wall correction factor kwall for 192Ir reference ionization chamber as a function of energy |
3.空腔电离室室壁修正kwall的变化规律
(1) 相同内径(5.8 cm)不同壁厚电离室kwall模拟:壁厚模拟必须满足电子平衡,本研究自制的球形石墨空腔电离室的石墨密度(1.85 g/cm3) 的最小壁厚为0.168 cm[12]。模拟壁厚选择范围为0.2~0.5 cm,结果如图 5所示。对于单能射线,电离室室壁越厚kwall越大,最大偏差为3.30%。在满足电子平衡的情况下,不同壁厚的电离室kwall整体变化规律相同,但较薄壁厚的电离室kwall更接近于1,修正份额更小,且随能量变化的范围也更小(能量响应)。

|
图 5 相同内径不同壁厚情况下kwall随能量变化 Figure 5 Variations of kwall with energy under the same inner diameter and different wall thickness |
(2) 相同壁厚(0.3 cm)不同内径对kwall的影响:如图 6所示,在壁厚相同的情况下,电离室内径越小,kwall越小,电离室对能量的响应越好,最大偏差为2.86%。

|
图 6 相同壁厚不同内径情况下kwall随能量变化 Figure 6 Variations of kwall with energy under the same wall thickness and different inner diameters |
讨论
实验测量的几何壁厚线性外推法是确定kwall最简单有效的方法,但是随着蒙特卡罗技术的发展,这种方法受到了质疑[13]。20世纪80年代,Rogers和Bielajew[14]首先利用蒙特卡罗方法进行了kwall的模拟计算,计算结果与实验几何壁厚外推结果存在差别。1990年Bielajew[15]根据模型,证明了利用线性外推的方法计算曲面电离室的室壁修正是不适合的,自此蒙特卡罗模拟计算的方法开始运用于修正因子的研究。
本研究通过蒙特卡罗软件EGSnrc对室壁修正系数进行了计算,模拟结果为1.037 7。室壁修正系数由散射修正因子和壁衰减修正乘积得到;本研究中能量对壁修正系数的影响,在低能部分kwall大小变化剧烈,考虑散射截面和NIST数据库中的光子在石墨中质能吸收系数曲线[16],在低能部分,γ光子射束转移给石墨的能量比较少,所以在低能部分kwall值主要是散射修正因子贡献;随着能量的增大,壁衰减修正因子和散射修正因子开始共同作用,kwall曲线趋于平缓。因此鉴于石墨空腔电离室的kwall修正系数的能量响应在低能部分波动较大,不建议用于300 keV以下低能射线的探测;而在>300 keV的能量段,kwall修正系数的能量响应最大偏差为1.62%。
此外,根据文献建议,对影响室壁修正系数kwall大小的光子能量、石墨密度、石墨壁厚和电离室内径进行了研究。根据文献,本研究中球形石墨空腔电离室的所用室壁材料石墨密度不影响模拟结果[17]。对于同一个球形石墨空腔电离室,光子能量以及电离室壁厚对室壁修正系数大小的影响,计算结果显示,随着能量的增大,球形石墨空腔电离室的室壁修正系数不断减小,在低能段变化剧烈,在高能段变化趋于平缓;在壁厚满足电子平衡条件下,随着壁厚的增加,kwall值也近似线性增加;在进行电离室设计时,为满足相关标准中对电离室能量响应不超过±4%的要求[18],可以考虑在满足电子平衡的情况下,将电离室的室壁适当减薄;对于相同壁厚(满足电子平衡)不同内径的球形石墨空腔电离室,保证探测信号合适,可以适当减少电离室内径大小。
本研究为高剂量率192Ir源参考空气比释动能率的绝对测量工作最重要的一环,拟尽快完成其他各项修正系数及物理常数的测量、模拟计算工作,完成参考空气比释动能率的量值复现,参加BIPM.R(I)-K8国际比对,并建立计量基准,在国内实现量值传递,为国内近距离治疗的质量控制工作提供量值溯源服务。
利益冲突 无
作者贡献声明 支世杰负责文献检索、论文撰写和修改;王继、吴金杰、王培玮和任世伟负责论文的审阅和修改
| [1] |
Hyer DE, Sheybani A, Jacobson GM, et al. The dosimetric impact of heterogeneity corrections in high-dose-rate 192Ir brachytherapy for cervical cancer: Investigation of both conventional point-A and volume-optimized plans[J]. Brachytherapy, 2012, 11(6): 515-520. DOI:10.1016/j.brachy.2012.01.011 |
| [2] |
Stromberg JS, Martinez AA, Horwitz EM, et al. Conformal high dose rate 192Ir boost brachytherapy in locally advanced prostate cancer: superior prostate specific antigen response compared to external beam treatment[J]. Cancer J Entif Am, 1997, 3(6): 346-352. |
| [3] |
Alvarez JT, Sander T, Pooter JD, et al. Comparison BIPM. RI(I)-K8 of high dose rate 192Ir brachytherapy standards for reference air kerma rate of the NPL and the BIPM[J]. Metrologia, 2014, 51(1A): 06024-06024. DOI:10.1088/0026-1394/51/1A/06024 |
| [4] |
International Commission on Radiation Units and Measurements. ICRU Report 90. Key data for ionizing-radiation dosimetry: Measurement standards and applications[R]. Bethesda: ICRU, 2016.
|
| [5] |
International Commission on Radiation Units Measurements. ICRU Report 58. Dose and volume specification for reporting interstitial therapy[R]. Bethesda: ICRU, 1998.
|
| [6] |
Gray LH. An ionization method for the absolute measurement of γ-ray energy[J]. Health Phys, 1980, 38(6): 907-918. DOI:10.1097/00004032-198006000-00004 |
| [7] |
Büermann L, Burns DT. Air-kerma cavity standards[J]. Metrologia, 2009, 46(2): 24-38. DOI:10.1088/0026-1394/46/2/S03 |
| [8] |
National Research Council Canada. The EGSnrc code system: Monte Carlo simulation of electron and photon transport[R]. Ottawa: NRCC, 2000.
|
| [9] |
Rogers D, Bielajew AF, Nahum AE. Ion chamber response and Awall correction factors in a 60Co beam by Monte Carlo simulation[J]. Phys Med Biol, 1985, 30(5): 429-433. DOI:10.1088/0031-9155/30/5/006 |
| [10] |
Seltzer SM, Bergstrom PM Jr. Changes in the U.S. primary standards for the air kerma from gamma-ray beams[J]. J Res Natl Inst Stand Technol, 2003, 108(5): 359-381. DOI:10.6028/jres.108.031 |
| [11] |
National Physical Laboratory. The NPL air kerma primary standard TH100C for high dose rate 192Ir brachytherapy sources [R]. London: NPL, 2006.
|
| [12] |
Goetsch SJ, Attix FH, Pearson DW, et al. Calibration of 192Ir high-dose-rate afterloading systems[J]. Med Phys, 1991, 18(3): 462-467. DOI:10.1118/1.596649 |
| [13] |
Rogers DW, Kawrakow I. Monte Carlo calculated correction factors for primary standards of air kerma[J]. Med Phys, 2003, 30(4): 521-532. DOI:10.1118/1.1563663 |
| [14] |
Rogers D, Bielajew AF. Wall attenuation and scatter corrections for ion chambers: measurements versus calculations[J]. Phys Med Biol, 1990, 35(8): 1065-1066. DOI:10.1088/0031-9155/35/8/003 |
| [15] |
Bielajew AF. On the technique of extrapolation to obtain wall correction factors for ion chambers irradiated by photon beams[J]. Med Phys, 1990, 17(4): 583-587. DOI:10.1118/1.596547 |
| [16] |
Hubbell JH. Photon mass attenuation and mass energy-absorption coefficients for H, C, N, O, Ar, and seven mixtures from 0.1 keV to 20 MeV[J]. Radiat Res, 1977, 70(1): 58-81. |
| [17] |
郝艳梅, 黄建微, 李德红, 等. 球形石墨空腔电离室壁修正因子模拟计算[J]. 计量学报, 2019, 40(3): 172-175. Hao YM, Huang JW, Li DH, et al. Simulation of wall correction factor of spherical graphite cavity ionization chamber[J]. Acta Metrol Sin, 2019, 40(3): 172-175. DOI:10.3969/j.issn.1000-1158.2019.03.28 |
| [18] |
国家质量监督检验检疫总局. JJG 912-2010治疗水平电离室剂量计检定规程[S]. 北京: 中国质检出版社, 2010. General Administration of Quality Supervision, Inspection and Quarantine. JJG 912-2010. Regulations for the verification of therapeutic level ionization chamber dosimeters[S]. Beijing: China Quality Inspection Press, 2010. |
 2022, Vol. 42
2022, Vol. 42


