2. 上海交通大学医学院附属瑞金医院放疗科, 上海 200025
2. Department of Radiation Oncology, Ruijin Hospital, Shanghai Jiaotong University School of Medicine, Shanghai 200025, China
放射治疗是肿瘤治疗的主要方式之一。质子“布拉格峰”的物理特性使质子治疗在精准控制肿瘤位置和保护正常组织方面有明显优势[1-3]。对于某些肿瘤,临床上已经验证了该优势[4-9]。
国产首台质子治疗装置采用自主研发的同步加速器,固定治疗室采用自主研发的质子笔形束点扫描控制系统[10],配套的质子治疗计划系统采用还未取得注册证的Raysearch laboratories AB公司的Raystation10B科研版。由于该治疗计划系统(TPS)作为整个装置的软件组件之一来获取注册证,而质子束流的参数调试需要与TPS的建模结果相匹配,因此,本研究将为该治疗计划系统建立束流模型,并通过初步剂量验证来测试模型精度。
Saini等[11]对商业治疗计划系统Raystation做了剂量验证的研究。Willis-Knighton癌症中心发现对于有射程调节器不同airgap的治疗计划,Raystation计划剂量比实际测量剂量偏高[12]。质子面剂量和体剂量的剂量验证可以参考γ指数判别准则[13-16]。但由于质子独特的能量沉积方式和射程不确定性,本研究将介绍国家食品药品监督管理总局(CFDA,现国家市场监督管理总局)发布的“质子碳离子治疗系统临床评价技术审查指导原则”中质子剂量验证的方法,并且根据实际测量验证的经验,给出了更加细化、可操作性强的质子剂量验证区域划分新方法。
材料与方法1. 水中积分深度剂量(IDD)曲线采集与建模:本研究采用实测的IDD曲线进行建模。将水箱(MP3-PL,PTW,扫描范围为500 mm × 408.5 mm × 500 mm)前窗用激光灯定位至等中心处。水箱前窗空气一侧中心轴线处放置一个参考电离室(Bragg peak chamber 34080,PTW),水箱内中心轴线放置测量电离室(Bragg peak chamber 34070,PTW),靠步进电机移动测量不同深度的剂量。束流采用单点扫描模式。模型中采集的IDD曲线为相对积分深度剂量分布曲线,以测量电离室与参考电离室的比值作为该测量点的相对剂量。测量电离室为圆柱形,敏感体积直径为8.16 cm。平坦区测量点的间距为2 mm,由于质子布拉格峰比较尖锐,为保证测量精度,布拉格峰附近测量点间距设置为0.2 mm。将测量所得的不同能量的IDD曲线导入Raystation10B科研版,并采用蒙特卡罗建模。由于实测IDD曲线都为标称能量,存在一定能散,每个实测IDD的能谱分布是通过该TPS的蒙特卡罗模拟库拟合得到。
2. 空气中的束斑建模:采用二维平面闪烁体探测器(Lynx PT,IBA)测量空气中不同能量等中心前后5个平面的束斑。5个平面分别距离等中心+150、+100、0、-100、-200 mm。Lynx采集的束斑是分辨率为0.5 mm的二维像素点矩阵。将相同坐标值对应的所有像素点累加分别得到x方向和y方向的高斯分布曲线。由于实测的束流位置存在一定偏差,为保证建模精度,需要将测量束斑的高斯中心移动到零位置。该科研版TPS基于Fermi-Eyges输运方程[17]描述的质子束斑在空气中的演化关系得到等中心处的束斑空间大小方差r2(0)、角方差θ2(0)和角度空间协方差rθ(0)。
3. 绝对剂量标定建模:由于质子治疗装置采用对应质子数(MU)来进行照射控制。所以需要标定不同能量下MU与剂量的对应关系。将水箱(MP3-PL,PTW)前窗用激光灯定位于等中心处。在不同能量下,用质子束流扫描点距为2.5 mm、照射野为10 cm×10 cm的方形均匀野,记录实际照射总的MU数。电离室PTW Markus23343置于中心轴线测量方野中心的剂量,电离室摆放的等效水深位置为1 cm与布拉格峰值一半所对应的深度的中间。通过蒙特卡罗建模计算得到不同能量下每MU对应的质子数(质子束/MU)曲线。
4. 测试材料、模体CT扫描方法:简单复杂度测试案例采用软件生成大小为50 cm × 50 cm × 50 cm的水模体Dicom文件。中等复杂度模体和高复杂度模体分别采用美国Radiology support devices INC公司加工的PMMA均匀密度双楔形板和半个头模体Male ART Head and Neck phantom (ART-210X)。此头模为仿真人头部模体,由软组织和骨骼等非均匀介质组成。采用荷兰飞利浦Brilliance TM Big Bore CT大孔经模拟定位机扫描模体。将双楔形板和半个头模体顶端两侧用胶带绑在固体水上进行CT扫描。胶带与固体水贴紧避免空气间隙。CT扫描的管电压为120 kV,电流时间积为200 mAs, 层厚和层间距都为2 mm,重建模式为iDose4 level3。
5. 治疗计划制定方法:将紧贴模体的固体水50 cm × 50 cm × 50 cm的区域勾画,并设置为纯水。由于该科研版TPS的CT值到阻止本领比(SPR)存在转换误差,所有模体都根据实际材料重设密度。半个头模的金标设为空气。靶区为10 cm×10 cm×10 cm立方体水靶。垂直于水箱零度一个射野。靶区物理剂量为181.8 cGy。靶区99%的体积达到处方剂量,10%的体积不超过190.9 cGy,靶区之外剂量尽量低。等中心为100 mm水深位置,治疗头到水箱前表面的距离为30 cm。简单复杂度案例浅层水靶的靶区深度为4~14 cm,对应照射能量为70.6~143.5 MeV。中等复杂度案例为束流穿过均匀介质双楔形模体的中等深度水靶,靶区深度为5~15 cm,对应照射能量为91.2~181.8 MeV。高复杂度案例为束流穿过非均匀介质半头模体的深层水靶,靶区深度为14~24 cm,对应照射能量为166.6~232.7 MeV。分别采用该科研版TPS自带的快速简化蒙特卡罗(MC)算法和笔形束(PB)算法计算中心轴线和垂直于束流中心轴线两个方向的剂量分布。
6. 摆位测量方法:模体必须紧贴水箱前壁,尽量避免空气间隙。采用德国IBA的DigiPhant PT v2.0 (540 mm×400 mm×400 mm)水箱测量。简单复杂度测试案例水箱中心轴线深度100 mm处定位于等中心。其他测试案例根据模体刻度线和金标定位,半个头模完成定位后去除金标再照射。用Markus 23343(PTW)电离室测量沿束流深度方向的剂量。根据等效水深计算电离室摆放位置。用二维平板点阵电离室MatriXX PT(IBA)测量横向剂量分布。
7. 剂量验证评价标准:根据“质子/碳离子治疗系统临床评价技术审查指导原则” [18],将剂量分布曲线分为4个区域。扩展布拉格峰(SOBP)平坦区定义为第1区,深度方向上升沿和后沿下降区、横向半影区都为2区,入射道定义为第3区,外部射束剂量下降接近零的区域为4区。对于不同复杂程度的测试案例,上述不同区的通过标准不同。分别计算治疗计划与实际测量剂量偏差的最大值和平均值。对于高剂量梯度的二区,由于非常小的位置偏差能够引起很大的剂量误差,故采用相同剂量点的位置偏差(DTA)准则来判定。对于简单复杂度案例,第1、3和4区测量点的平均偏差和最大偏差都不超过5%,第2区最大偏差不超过10%或DTA不超过2 mm。对中等复杂度案例,第1、3区测量点的平均偏差和最大偏差都不超过5%;第4区最大偏差不超过6%,平均偏差不超过5%;第2区最大偏差不超过15%或DTA不超过3 mm。对高复杂度案例,第1、3区测量点的平均偏差不超过5%,最大偏差不超过6%;第4区最大偏差不超过7%,平均偏差不超过5%;第2区最大偏差不超过15%或DTA不超过3 mm。
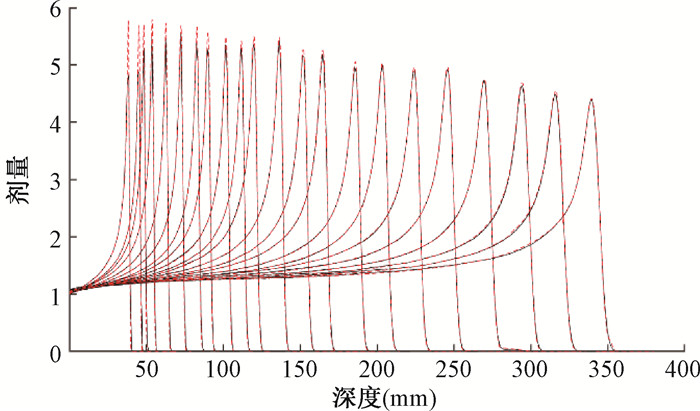
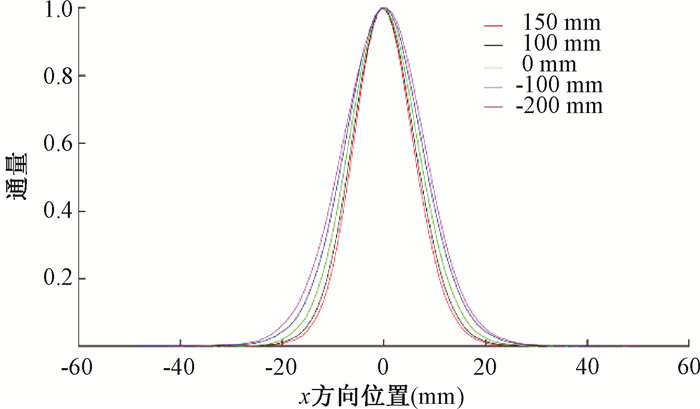
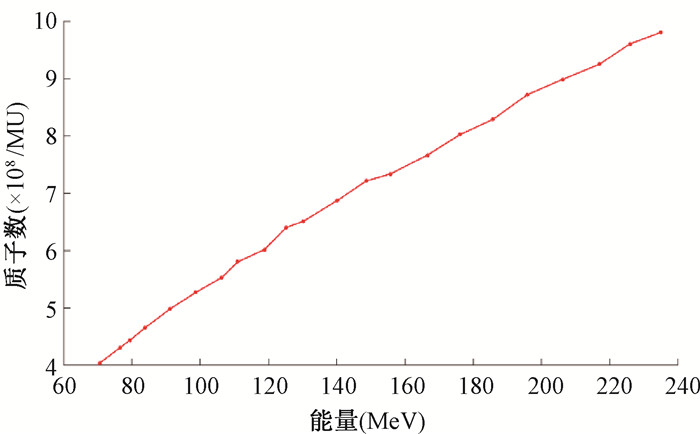
结果1. 治疗计划系统Raystation10B科研版建模结果: 图 1为水中不同能量的IDD曲线建模结果。红色虚线为导入TPS建模的实测数据。黑色实线为该科研版TPS蒙特卡罗建模拟合曲线。该TPS通过蒙特卡罗拟合得到每个标称能量相应的能谱分布来进行剂量计算。从图中看出,射程拟合准确,中高能部分的IDD峰值曲线模型拟合的很好,但低能部分建模拟合的IDD峰值比实测值偏低。图 2为70 MeV能量下测量的空气中等中心前后5个平面(+150、+100、0、-100、-200 mm)x方向的高斯分布曲线。其中,0 mm为等中心平面。从图 2看出,离质子源越远的平面(-200 mm),束斑越大,符合Fermi-Eyges输运方程规律。该科研版TPS根据不同能量束斑在空气中的演化规律(Fermi-Eyges输运方程)来建模。图 3为该TPS绝对剂量标定建模后得到的不同能量下每MU对应的质子数。能量越高,每MU对应的质子数越大。绝对剂量标定曲线对绝对剂量的建模精度起关键作用。
|
图 1 水中IDD曲线建模 Figure 1 Modeling of IDD curves in water |
|
图 2 能量70 MeV下空气中5个平面x方向束斑 Figure 2 Five beam spot profiles in air in the x direction on the plane under proton energy of 70 MeV |
|
图 3 不同能量绝对剂量标定建模 Figure 3 Calibration and modeling under different energy levels |
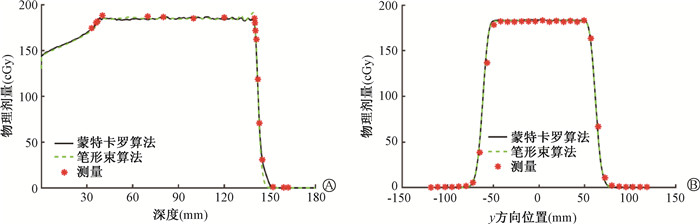
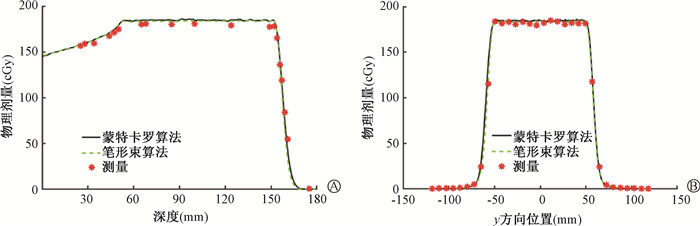
2. 治疗计划系统Raystation10B科研版剂量验证结果:图 4~6分别为简单复杂度、中等复杂度和高复杂度测试案例治疗计划计算与实际测量的剂量分布对比图。左图和右图分别为沿束流方向和垂直于束流方向的剂量分布。黑色实线和绿色虚线分别为TPS蒙特卡罗算法和质子笔形束算法计算的剂量分布曲线。红色点为实际测量的剂量值。与Geant4等蒙特卡罗算法不同之处是Raystation10B科研版MC算法为简化版快速蒙特卡罗算法。
|
图 4 实际测量与治疗计划剂量分布比较(简单复杂度水模体) A.深度方向;B. y方向 Figure 4 Comparation of dose distributions measured and calculated by the TPS (low-complexity water phantom) A. Depth direction; B. y direction |
|
图 5 实际测量与治疗计划剂量分布比较(中等复杂度双楔形模体) A.深度方向;B. y方向 Figure 5 Comparation of dose distributions measured and calculated by the TPS (medium-complexity double wedge phantom) A. Depth direction; B. y direction |
|
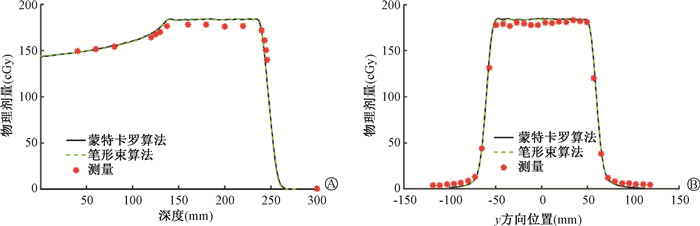
图 6 实际测量与治疗计划剂量分布比较(高复杂度半头模体) A.深度方向;B. y方向 Figure 6 Comparation of dose distributions measured and calculated using the TPS (high-complexity half head phantom) A. Depth direction; B. y direction |
从图中看出,该TPS蒙特卡罗算法和质子笔形束算法只在高剂量梯度处有微小差别,蒙特卡罗算法比笔形束算法更加平滑和精确。整体上实际测量剂量与TPS计算剂量吻合较好。对于简单复杂度案例(图 4),后端剂量下降distal fall-off仅为3.40 mm。9 cm水深平面处横向半影为8.49 mm;深度方向2区上升沿和下降沿采用蒙特卡罗算法计算的平均DTA为0.33和0.16 mm;深度方向靶区测量值和计算值的平均偏差为1.70 %,垂直于束流y方向的平均偏差仅为0.65 %,远小于通过标准的±5 %。对于中等复杂度案例(图 5),后端剂量下降distal fall-off为5.69 mm;6 cm水深平面处横向半影为7.39 mm;深度方向靶区采用蒙特卡罗算法计算的平均偏差为2.69 %,第2区下降沿平均DTA为0.54 mm。对于高复杂度案例(图 6),深度方向靶区实际测量平均剂量比该TPS采用PB算法计算的平均剂量偏低3.58 %;剂量下降后沿平均DTA为1.46 mm;后沿剂量下降distal fall-off为10.6 mm;19 cm水深平面处横向半影为9.7 mm。各测试案例均满足国家型式检测的剂量验证要求,因此,总体上TPS建模精度较好。
讨论本研究介绍了治疗计划系统Raystatio10B科研版的建模与初步剂量验证方法,并且通过剂量验证结果分析了建模精度。总体上剂量验证满足国家型式检测要求,模型精确。但低能区模型拟合的IDD峰值比实测偏低主要可能原因:①由于低能布拉格峰非常尖锐而该TPS蒙特卡罗分辨率为1 mm,远大于实测布拉格峰的分辨率0.2 mm。②该TPS蒙特卡罗库的低能IDD与“国产首台质子治疗装置”低能IDD能散匹配不佳。需要通过调试加速器低能区IDD的能散尽量与模型相匹配。
高复杂度案例靶区整体实测剂量比治疗计划略微偏低,可能是高能区的绝对剂量建模质子/MU偏高导致,这可能与扫描点的位置和剂量偏差导致方野剂量分布不够均匀有关。另一方面,由于该TPS的HU值到SPR的转换有一定误差,本研究根据模体的实际材料进行密度设置,而半个头模结构复杂、密度不均匀,密度设置偏差较大。该TPS的HU值到SPR的转换精度将另行通过对动物组织的实测来进行验证。
本研究在满足“质子/碳离子治疗系统临床评价技术审查指导原则”剂量梯度区 <10%/mm为1区,剂量梯度>10%/mm为2区定义的前提下,根据剂量验证的实际经验建立了一套更加细化、可操作性更强的区域划分新方法。将靶区前端对应能量的IDD曲线前沿布拉格峰值剂量的60%所对应深度位置定义为深度剂量分布曲线中2区与入射道3区的分界点。将靶区后端对应能量的IDD曲线后沿布拉格峰值剂量的1% 所对应的深度位置定义为深度剂量分布曲线中2区与4区分界点。
利益冲突 无
志谢 本研究获得首台国产质子治疗示范装置,上海市自主创新和高新技术产业发展重大项目〔沪发改高技(2012)016号〕资助
作者贡献声明 孔海云负责实验测量、数据分析和论文撰写;贺晓东负责测量方案讨论、论文思路
| [1] |
Newhauser WD, Zhang R. The physics of proton therapy[J]. Phys Med Biol, 2015, 60(8): 155-209. DOI:10.1088/0031-9155/60/8/R155 |
| [2] |
Bortfeld T. An analytical approximation of the Bragg curve for therapeutic proton beams[J]. Med Phys, 1997, 24(12): 2024-2033. DOI:10.1118/1.598116 |
| [3] |
Weyrather WK, Debus J. Particle beams for cancer therapy[J]. Clin Oncol (R Coll Radiol), 2003, 15(1): 23-28. DOI:10.1053/clon.2002.0185 |
| [4] |
Fan C, Li Y, Liu Q. Advantages of proton therapy in non-small cell lung cancers[J]. Cancer Biother Radiopharm, 2013, 28(3): 183-186. DOI:10.1089/cbr.2012.1343 |
| [5] |
Clair WHSt, Adams JA, Bues M, et al. Advantage of protons compared to conventional X-ray or IMRT in the treatment of a pediatric patient with medulloblastoma[J]. Int J Radiat Oncol Biol Phys, 2004, 58(3): 727-734. DOI:10.1016/S0360-3016(03)01574-8 |
| [6] |
van de Water TA, Bijl HP, Schilstra C, et al. The potential benefit of radiotherapy with protons in head and neck cancer with respect to normal tissue sparing: a systematic review of literature[J]. Oncologist, 2011, 16(3): 366-377. DOI:10.1634/theoncologist.2010-0171 |
| [7] |
Fagundes M, Hug EB, Pankuch M, et al. Proton therapy for local-regionally advanced breast cancer maximizes cardiac sparing[J]. Int J Part Ther, 2015, 1(4): 827-844. DOI:10.14338/IJPT-14-00025.1 |
| [8] |
Weber DC, Langendijk JA, Grau C, et al. Proton therapy and the European Particle Therapy Network: The past, present and future[J]. Cancer Radiother, 2020, 24(6-7): 687-690. DOI:10.1016/j.canrad.2020.05.002 |
| [9] |
Courdi A, Caujolle JP, Grange JD, et al. Results of protontherapy of uveal melanomas treated in nice[J]. Int J Radiat Oncol Biol Phys, 1998, 42(1): 331-331. DOI:10.1016/S0360-3016(98)80515-4 |
| [10] |
苗春晖, 刘鸣, 舒航, 等. 质子点扫描照射位置控制系统设计[J]. 核技术, 2018, 41(4): 40201-040201. Miao CH, Liu M, Shu H, et al. Design of a proton spot scanning position control system[J]. Nuc Tech, 2018, 41(4): 40201-040201. DOI:10.11889/j.0253-3219.2018.hjs.41.040201 |
| [11] |
Saini J, Cao N, Bowen SR, et al. Clinical commissioning of a pencil beam scanning treatment planning system for proton therapy[J]. Int J Part Ther, 2016, 3(1): 51-60. DOI:10.14338/IJPT-16-0000.1 |
| [12] |
Pidikiti R, Patel BC, Maynard MR, et al. Commissioning of the world's first compact pencil-beam scanning proton therapy system[J]. J Appl Clin Med Phys, 2018, 19(1): 94-105. DOI:10.1002/acm2.12225 |
| [13] |
Bakai A, Alber M, Nüsslin F. A revision of the gamma-evaluation concept for the comparison of dose distributions[J]. Phys Med Biol, 2003, 48(21): 3543-3553. DOI:10.1088/0031-9155/48/21/006 |
| [14] |
Depuydt T, Van Esch A, Huyskens DP, et al. A quantitative evaluation of IMRT dose distributions: refinement and clinical assessment of the gamma evaluation[J]. Radiother Oncol, 2002, 62(3): 309-319. DOI:10.1016/S0167-8140(01)00497-2 |
| [15] |
Low DA, Harms WB, Mutic S, et al. A technique for the quantitative evaluation of dose distributions[J]. Med Phys, 1998, 25(5): 656-661. DOI:10.1118/1.598248 |
| [16] |
Low DA, Dempsey JF. Evaluation of the gamma dose distribution comparison method[J]. Med Phys, 2003, 30(9): 2455-2464. DOI:10.1118/1.1598711 |
| [17] |
Kanematsu N. Alternative scattering power for Gaussian beam model of heavy charged particles[J]. Nucl Instrum Meth B, 2008, 266(23): 5056-5062. DOI:10.1016/j.nimb.2008.09.004 |
| [18] |
国家市场监督管理总局. 质子碳离子治疗系统临床评价技术审查指导原则. 附录IX. 治疗计划系统要求[Z]. 北京: 国家市场监督管理总局, 2018. State Administration for Market Regulation. Guidelines for technical review of clinical evaluation of proton carbon ion therapy systems. Appendix 6. Treatment planning system requirements[Z]. Beijing: State Administration for Market Regulation, 2018. |
 2022, Vol. 42
2022, Vol. 42


