2. 中国科学院上海应用物理研究所,上海 201800;
3. 上海市质子重离子医院 上海市质子重离子放射治疗工程技术研究中心放射物理科 201315
2. Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Shanghai 201800, China;
3. Department of Medical Physics, Shanghai Proton and Heavy Ion Center, Shanghai Engineering Research Center of Proton and Heavy Ion Radiation Therapy, Shanghai 201315, China
目前商用点扫描碳离子治疗计划系统(treatment planning system, TPS)的优化计算大多基于卷积叠加算法,在临床使用中具有局限性。例如,在应用射程位移器(range shifter, RS)治疗浅表肿瘤时,经TPS计算的绝对剂量与实际输运的剂量存在不可忽略的差异[1]。粒子在肺部多孔隙组织中输运时,实验观察到布拉格峰退化[2],目前TPS的卷积叠加算法并未考虑该效应,研究者往往需要通过蒙特卡罗(Monte Carlo,MC)模拟方法来评估靶区覆盖的不足及正常组织剂量的升高[3-4]。临床使用的TPS的基础数据如碳离子及次级粒子能谱、积分深度剂量曲线等,也经常借助MC模型来计算获得[5]。
蒙特卡罗程序包括FLUKA、MCNP、Geant4等都是粒子输运的主要应用的模拟程序[6-8],多项研究通过匹配所在粒子放疗中心的实验数据建立了配套的粒子输运束流MC模型[5-10],而应用MC模拟程序建立的束流模型也为粒子放疗的临床验证或研究工作提供了便利。Almhagen等[11]与Grevillot等[12]分别使用TOPAS和Geant4建立了质子束流的笔形束模型;Nelson等[10]使用TOPAS建立了质子束流笔形束的动态准直模型。本研究利用上海市质子重离子医院同步加速器点扫描碳离子束流放射治疗系统的束流参数,使用MC程序FLUKA建立同步加速器碳离子束流MC模型,并通过使用γ分析方法验证了模型的准确性。
材料与方法1. 参数预设置:本研究所有模拟均使用了FLUKA(4-1.1, CERN)的“HADROTHErapy”预设模式,并加入了标准的核蒸发模型,在该设定下,热中子的输运阈值(transport threshold)为10-5eV,而其他粒子的输运阈值为100 keV。此外,x、y方向的束斑形状、束流初始能谱分布与角分布都设置为高斯分布。对于能量高于100 MeV/u的碳离子,通过FLUKA的“ldpmqmd”链接编译了用于实现碳离子核相互作用的可执行文件。
模拟工作所使用的计算机硬件与盛尹祥子等[13]在建立点扫描质子束流治疗头时所用的配置相同,以能量为234.05 MeV/u的碳离子束流为例,输入1×108个初始粒子数可使最大剂量5%以上计数区域内的统计误差控制在1%之内,所需单核CPU计算时间为93 h。
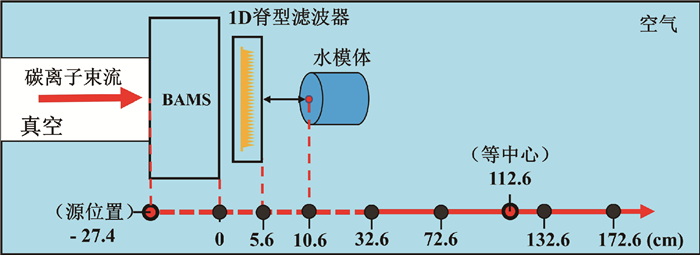
2. 几何模型的建立:在束流应用和监控系统(beam application and monitoring system,BAMS)的模型建立工作方面,参考了盛尹祥子等[9-13]建立的SPHIC质子束流模型时所用到的BAMS尺寸、位置参数与材料种类。与质子模型不同,碳离子治疗头需要加入脊型滤波器(ripple filter, RiFi),参考了SPHIC临床使用的1D-RiFi的实际参数,建立了具有精细的周期性凹槽结构1D-RiFi。1D-RiFi以PMMA为填充材料,厚度(平行于束流方向)为2.7 mm,其中包括0.3 mm的基底,凹槽结构的周期间隔为1.0 mm。在建立1D-RiFi的几何模型时,使用了FLUKA中的LATTICE卡和ROT-DEFI卡来完成对精细周期性凹槽结构的重复编辑。最终在FLUKA中建立的碳离子治疗头几何模型及其位置如图 1所示。
|
图 1 在蒙特卡罗程序FLUKA中建立的同步加速器碳离子治疗头的几何结构及其相对位置 Figure 1 The geometric structure and relative location of synchrotron treatment nozzle modelled in MC code FLUKA |
3. 束流模型的建立:SPHIC的碳离子束流是点扫描束流,束流主要物理参数包括束流能量与能谱、束斑大小以及束流强度。在FLUKA中,需要调整束流标称能量、高斯能谱分布、初始束斑大小以及束流的角分布匹配上述物理参数。通过FLUKA中的用户自定义文件“source.f”进行源项定义与参数匹配。
(1) 积分深度剂量分布(integrate depth dose, IDD)的匹配:在SPHIC的离子束特性表(list of ion beam characteristics, LIBC)中,碳离子束流能量从86.22 MeV/u到430.12 MeV/u,共291个能量层,涵盖的射程范围为2~31 cm,选取SPHIC在年检时使用PEAKFINDER(德国PTW)测量的15组能量的IDD作为纵向剂量分布的参考。FLUKA模拟中,在10.6 cm处建立了一个半径为15 cm、长40 cm的(圆柱)水模体,模拟过程选择的计数半径为4.08 cm,从而与IDD测量时PEAKFINDER的探测面积保持一致[5],束流方向计数分辨率选择了0.2 mm。通过在FLUKA中调整标称能量获得一致的束流射程,调整高斯能谱分布获得一致的布拉格峰宽度(定义为布拉格峰前后80%最大剂量之间的深度距离)。
(2) 束斑大小(full width half maximum,FWHM)的匹配:在SPHIC的LIBC中,碳离子每个能量层有5种不同尺寸的束斑,以234.05 MeV/u能量层为例,第1到第5组束斑大小分别为:4.5、5.9、7.3、8.8、10.2 mm。选择了每个能量层中≥6 mm的第1个束斑作为匹配的目标参数。因实际束流具有一定的角分布且会受到输运路径上各类介质的散射,束流的束斑大小会随着输运距离的变化而变化,选取了等中心(112.6 cm) 及其上下游(72.6、132.6 cm)共3个位置作为参考点,与使用EDR2胶片(美国Carestream Health公司)测得的束斑大小进行了匹配,束斑测量的具体实验方法与盛尹祥子等[9]所介绍的内容一致。
Fermi-Eyges理论[14]给出了束流角分布、角分布协方差以及束斑尺寸随束流输运距离的关系,如式1~3:
| $ \bar{\theta}^{2}(z)=\bar{\theta}^{2}(0)+\int\limits_{0}^{z} T \times \mathrm{d} z^{\prime} $ | (1) |
| $ \overline{r \theta}(z)=\overline{r \theta}(0)+\bar{\theta}^{2}(0) \times z+\int\limits_{0}^{z}\left(z-z^{\prime}\right) T \times \mathrm{d} z^{\prime} $ | (2) |
| $ \begin{gathered} \bar{r}^{2}(z)=\bar{r}^{2}(0)+2 \times \overline{r \theta}(0) \times z+ \\ \bar{\theta}^{2}(0) \times z^{2}+\int\limits_{0}^{z}\left(z-z^{\prime}\right)^{2} T \times \mathrm{d} z^{\prime} \end{gathered} $ | (3) |
式中,θ为束流角分布;rθ为角分布协方差;r为束斑尺寸(以σ表示,σ=FWHM/2.355);T为散射因子;z为束流相对初始位置(0 cm)输运的距离。当束流在空气中输运时,T≈0。测量了15组能量下治疗头下游5个位置(32.6、72.6、112.6、132.6、和172.6 cm)的束斑大小,通过公式3推算出了模型源平面位置(-27.4 cm)的初始束斑尺寸与角分布,考虑到治疗头内存在的微米级非空气介质会对束流造成额外的散射,需要对计算得到的初始角分布进行了微调以实现理想的匹配效果。计算过程没有考虑空气中的多重库伦散射对束流角分布的影响,认为束流角分布在束流输运过程中保持不变。
SPHIC使用EDR2胶片进行束斑大小的测量,使用Vidar scanner (VIDAR Systems Corporation, VA)扫描冲洗后的胶片,在FLUKA中设置了与EDR2几何尺寸相同的立方体计数区域(20 cm × 20 cm × 0.2 cm)进行计数,并选择了与其扫描分辨率一致的计数分辨率(0.36 mm),选择空气作为计数区域的介质;与Syngo® TPS(VC13C, SIEMENS, 德国)的设置相同,将x和y方向的束斑大小设置为相同值。
(3) 数据拟合:粒子束流的参数需要随能量变化而平滑且连续的变化[11],需要使用现有模拟中的标称能量产生临床需要的全部能量及其它束流参数,故选择了使用线性拟合来获取标称能量的函数,使用四次多项式拟合获得连续的高斯能谱分布、初始束斑大小以及束流的角分布。其中,每组能量中相同档位的束斑大小是随能量变化而单调变化的,而本研究中束斑大小的匹配目标参数是每个能量层中≥6 mm的最接近的束斑大小。按照上述要求,碳离子86.22~165.61 MeV/u能量区域匹配的是第1档束斑,165.61~231.62 MeV/u匹配的是第2档束斑,231.62~ 430.12 MeV/u匹配的是第3档束斑。因此,在束斑大小的拟合过程中应用了分段四次多项式拟合的方法,以获得更加精确的拟合数据。
4. 束流模型的验证:使用Syngo® TPS在等中心处生成了一个尺寸为30 cm×30 cm×40 cm的水模体作为输运介质,在其内部勾画了3组立方体靶区,并相应制定了使用1D-RiFi调制后的靶区治疗计划,为保证射野的横向剂量的均匀分布,相邻两个扫描点的间隔(spot spacing)设为2 mm,深度方向步长设为3 mm,通过TPS与FLUKA输出的剂量分布比较来验证模型的准确性。立方体靶区的尺寸(modulation width, M)和中心深度(center depth, CD)分别为3、6、9 cm,以及6、12、24 cm,如M3CD6为6 cm的深度下边长为3 cm的立方体靶区。其中,靶区M3CD6的治疗计划选取了能量范围在143.38 ~192.92 MeV/u之间的12组能量;靶区M6CD12选取了208.94~283.19 MeV/u之间的22组能量;靶区M9CD24选取了326.85~ 414.31 MeV/u之间的32组能量,制定治疗计划的处方物理剂量均为1 Gy。另外,选取了3例头颈部肿瘤患者的治疗计划,共包括6个射野,所使用的能量范围为86.22~ 293.91 MeV/u,能量层数量为33~45。将治疗计划中的束流参数导入“source.f”文件,从而实现在FLUKA中的源项创建。
FLUKA中探测器卡所用的计数分辨率与TPS优化网格间距一致(x、y、z方向均为2 mm)。利用内部开发的程序将FLUKA计算得到的三维剂量分布转为剂量DICOM文件,并使用VeriSoft 7.1(德国PTW-Freiburg)将FLUKA与TPS输出的剂量分布进行了2D-与3D-γ分析检验。采用了3 mm/3%和2 mm/2%的γ分析标准,分析范围设定在10%最大剂量以上,并分别使用整体最大剂量(global maximum dose)对所选的两组数据进行了归一化,将结果以百分比通过率的形式输出。
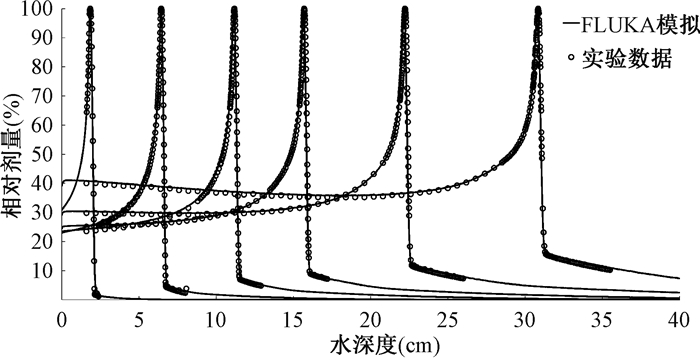
结果1. IDD和束斑:图 2为6组单能碳离子束流IDD的匹配结果,其中FLUKA模拟IDD曲线与实验测量的IDD曲线均分别进行了归一化处理,每组匹配的布拉格峰宽度差异不超过0.05 mm(2.81%),射程深度差异不超过0.02 mm(0.33%),后沿半影宽度(distal falloff width, DFW)差异也稳定在0.1 mm以内。
|
图 2 同步加速器引出的不同射程深度的碳离子束流在水中积分深度剂量曲线的FLUKA模拟与实验测量的对比 Figure 2 Comparison between FLUKA simulation and measured IDD curves for carbon ion beams from synchrotron with different ranges in water |
表 1为FLUKA模拟束斑大小与实验测量的束斑大小在5个不同位置的比较情况,平均绝对偏差±标准差(百分比偏差平均值±标准差)为0.05 mm ± 0.04 mm(0.66%±0.57%),最大偏差为0.17 mm (2.40%,能量为430.12 MeV/u的碳离子束流在72.6 cm位置的结果)。
|
|
表 1 同步加速器引出的各能量碳离子束流在不同治疗头下游位置束斑大小的测量与模拟结果(mm) Table 1 Simulation and measurement of spot sizes of carbon ion beams from synchrotron with different energy levels and positions downstream of the treatment nozzle (mm) |
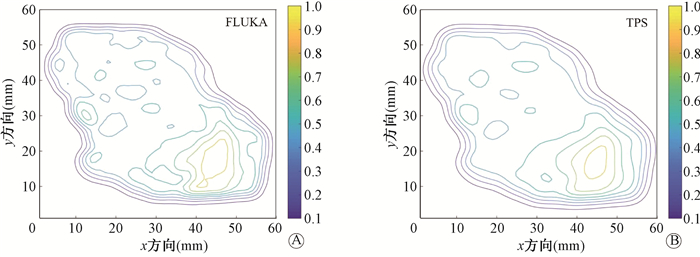
2. 模拟验证:在3 mm/3%的标准下,2D-与3D-γ通过率均在99%以上。表 2为不同靶区在2 mm/2% 的标准下2D-与3D-γ通过率,其中γ通过率全部在95%以上。图 3为第1例头颈部肿瘤患者(射野1)靶区中2D剂量分布对比,该靶区在2 mm/2%标准的2D-γ通过率为96%。
|
|
表 2 在2 mm/2%的标准下,不同靶区的FLUKA模拟相对于TPS计算的2D-与3D-γ通过率(%) Table 2 2D- and 3D-γ pass rates under the criteria of 2 mm/2% of dose distribution between TPS and FLUKA in different targets(%) |
|
注:FLUKA为本研究所使用的蒙特卡罗模拟程序;TPS为本研究所使用的治疗计划系统,即Syngo® TPS 图 3 第1例头颈部肿瘤患者(射野1)靶区中2D剂量分布图 A. FLUKA模拟结果;B. TPS计算结果 Figure 3 2D dose distributions in head and neck tumor of a first patient (field 1) A. FLUKA simulation; B. TPS calculation |
讨论
本研究主要参考了盛尹祥子等[9]与Parodi等[5]的建模方法,使用了MC程序FLUKA建立了SPHIC碳离子束流模型,在单能束流参数匹配的中调整了束流标称能量、能谱、初始束斑大小以及束流的角分布来匹配实验测量数据,真实的还原了束流与介质相互作用的物理过程与结果。剂量对比结果表明,各立方体靶区计划的FLUKA模拟结果与TPS剂量分布的γ通过率均超过95%,能够达到与临床治疗计划进行比较验证的目的。
单能碳离子束流的IDD匹配结果显示,使用FLUKA模拟的IDD曲线在入口处的相对剂量均高于实验测量的结果,主要原因是FLUKA内置的阻止本领(stopping power)模型与实际测量之间存在一定的差异[15],最终导致模拟IDD曲线在入口处的相对剂量偏高。此外,不同于质子束流,碳离子束流与物质相互作用后会产生裂变碎片,出现布拉格峰后的拖尾现象,由于这些裂变碎片在束流射程末端产生的混合辐射场较为复杂,导致FLUKA模拟结果和实验结果产生差异[5]。
在单能碳离子束流的束斑匹配过程中,Parodi等[5]定义了初始束斑尺寸来匹配碳离子束斑的大小,而没有考虑束流的角分布;盛尹祥子等[9]在进行质子束流模型的束斑大小匹配时,将质子源定义为了一个初始束斑大小为0 mm的点源,通过调整束流的角分布得到的结果与参考值的平均差异在5%之内。碳离子受到的散射效果的影响相对较小,如果仅通过束流角分布来影响束斑大小则很难在等中心及束流上下游实现很好的匹配效果,此外,当碳离子束流以一个点源作为初始束斑大小通过1D-RiFi后,无法得到稳定的展宽效果与横向剂量分布。仅以初始束斑进行匹配而不考虑角分布时,很难在低能碳离子束流的情况下实现理想的匹配结果,所以本研究通过参考Fermi-Eyges理论引入了初始束斑尺寸和束流角分布两个变量,最终将束斑大小偏差限制在了0.2 mm之内,亦在束斑大小质量保证(quality assurance,QA)的差异限值(10%)之内。
在MC模型验证的标准方面,Paganetti等[16]使用Geant4建立了马萨诸塞州总院的质子治疗头模型,并使模拟与实验得到的扩展布拉格峰深度差异小于1 mm;Sayah等[17]使用MCNPX建立的质子束流模型将相对剂量下束流参数的最大差异限制在了2 mm之内;在Almhagen等[11]使用GATE建立的笔形束质子束流模型中,2 mm/3%标准下的各深度2D剂量分布均在95%之上。本研究使用FLUKA建立的束流模型所采用的验证指标参考了盛尹祥子等[9]在建立质子束流模型是所采用的γ分析标准:2 mm/2%与3 mm/3%,γ分析结果显示2D、3D情况下的通过率均在95%(2 mm/2%)与99%(3 mm/3%)以上,说明了模型的可靠性。本研究的不足之处在于,仅选取了Syngo® TPS计算得到的剂量分布对碳离子蒙特卡罗模型进行剂量验证。Deng等[18]对Syngo® TPS的质子和碳离子剂量计算算法进行了测量验证,证实了其物理剂量计算结果具有较高的可靠性,然而在条件允许时,仍推荐采用实际测量对蒙特卡罗模拟计算的剂量分布进行实验验证;另外,束流模型的剂量分布模拟计算和剂量比较均是在水模体中进行的,并没有基于CT图像进行剂量计算和比较。
本研究使用FLUKA建立的点扫描碳离子束流模型与TPS输出结果具有较好的一致性,能够实现束流输运过程的精准模拟。该MC模型不仅可用于临床治疗计划的模拟验证[9]以节约束流时间,其应用范围还可以进一步扩展到新粒子治疗设备在开发阶段的模拟、LET分布模拟以及生物有效剂量计算。
利益冲突 全体作者未因进行该研究而接受任何不正当职务或财务利益,在此对研究的独立性和科学性予以保证
作者贡献声明 董思学负责束流参数匹配与数据整理,撰写论文;夏晓彬指导论文修改;盛尹祥子负责指导研究方案、开发计算程序并协助修改论文
| [1] |
Nichiporov D, Moskvin V, Fanelli L, et al. Range shift and dose perturbation with high-density materials in proton beam therapy[J]. Nucl Instrum Methods Phys Res B, 2011, 269(22): 2685-2692. DOI:10.1016/j.nimb.2011.07.109 |
| [2] |
Hranek A, Resch AF, Georg D, et al. Investigation of the Bragg peak degradation caused by homogeneous and heterogeneous lung tissue substitutes: proton beam experiments and comparison to current clinical dose calculation[J]. Phys Med Biol, 2020, 65(24): 5024-5036. DOI:10.1088/1361-6560/abc938 |
| [3] |
Baumann KS, Witt M, Weber U, et al. An efficient method to predict and include Bragg curve degradation due to lung-equivalent materials in Monte Carlo codes by applying a density modulation[J]. Phys Med Biol, 2017, 62(10): 3997-4016. DOI:10.1088/1361-6560/aa641f |
| [4] |
Flatten V, Baumann KS, Weber U, et al. Quantification of the dependencies of the Bragg peak degradation due to lung tissue in proton therapy on a CT-based lung tumor phantom[J]. Phys Med Biol, 2019, 64(15): 5005-5015. DOI:10.1088/1361-6560/ab2611 |
| [5] |
Parodi K, Mairani A, Brons S, et al. Monte Carlo simulations to support start-up and treatment planning of scanned proton and carbon ion therapy at a synchrotron-based facility[J]. Phys Med Biol, 2012, 57(12): 3759-3784. DOI:10.1088/0031-9155/57/12/3759 |
| [6] |
Ferrari A, Sala PR, Fasso A, et al. FLUKA: A multi-particle transport code[M]. United States: SLAC National Accelerator Lab., Menlo Park, CA, 2005.
|
| [7] |
Denise BP. MCNPXTM user's manual version 2.7.0[M]. LOS Alamos: Los Alamos National Laboratory, 2005.
|
| [8] |
Agostinelli S, Allison J, Amako K, et al. Geant4-a simulation toolkit[J]. Nucl Instrum Methods Phys Res, 2003, 506(3): 250-303. DOI:10.1016/S0168-9002(03)01368-8 |
| [9] |
Sheng Y, Wang W, Huang Z, et al. Development of a Monte Carlo beam model for raster scanning proton beams and dosimetric comparison[J]. Int J Radiat Biol, 2020, 96(11): 1435-1442. DOI:10.1080/09553002.2020.1812758 |
| [10] |
Nelson NP, Culberson WS, Hyer DE, et al. Development and validation of the dynamic collimation Monte Carlo simulation package for pencil beam scanning proton therapy[J]. Med Phys, 2021, 48(6): 3172-3185. DOI:10.1002/mp.14846 |
| [11] |
Almhagen E, Boersma DJ, Nyström H, et al. A beam model for focused proton pencil beams[J]. Phys Med, 2018, 52: 27-32. DOI:10.1016/j.ejmp.2018.06.007 |
| [12] |
Grevillot L, Bertrand D, Dessy F, et al. A Monte Carlo pencil beam scanning model for proton treatment plan simulation using GATE/GEANT4[J]. Phys Med Biol, 2011, 56(16): 5203-5219. DOI:10.1088/0031-9155/56/16/008 |
| [13] |
盛尹祥子, KambizS, 王巍伟, 等. 点扫描质子束治疗机头的蒙特卡罗模拟和验证[J]. 中华放射医学与防护杂志, 2019, 39(8): 635-640. Sheng YXZ, Kambiz S, Wang WW, et al. Monte Carlo simulation and verification of a scanning proton beam nozzle[J]. Chin J Radiol Med Prot, 2019, 39(8): 635-640. DOI:10.3760/cma.j.issn.0254-5098.2019.08.014 |
| [14] |
Gottschalk B. Techniques of proton radiotherapy: transport theory[J/OL]. arXiv: 1204.4470, 2012[2012-04-29]. https://ui.adsabs.harvard.edu/abs/2012arXiv1204.4470G.
|
| [15] |
Mairani A, Brons S, Cerutti F, et al. The FLUKA Monte Carlo code coupled with the local effect model for biological calculations in carbon ion therapy[J]. Phys Med Biol, 2010, 55(15): 4273. DOI:10.1088/0031-9155/55/15/006 |
| [16] |
Paganetti H, Jiang H, Lee SY, et al. Accurate Monte Carlo simulations for nozzle design, commissioning and quality assurance for a proton radiation therapy facility[J]. Med Phys, 2004, 31(7): 2107-2118. DOI:10.1118/1.1762792 |
| [17] |
Sayah R, Donadille L, Aubé A, et al. Monte Carlo simulation of a proton therapy beamline for intracranial treatments[J]. Radioprotection, 2013, 48(3): 317-339. DOI:10.1051/radiopro/2012054 |
| [18] |
Deng Y, Wang Q, Huang Z. Field size analysis of patient-specific quality assurance in scanned carbon ion radiotherapy[J]. Med Phys, 2021, 48(11): 6627-6633. DOI:10.1002/mp.15279 |
 2022, Vol. 42
2022, Vol. 42


