为免受电离辐射的不利影响,既要防止组织反应,即确定性效应,同时也要限制癌症风险和遗传效应,即随机性效应。为满足这些要求,国际放射防护委员会(International Commission on Radiological Protection, ICRP)在第103号出版物中定义了与风险相关的剂量学量-防护量(protection quantities):器官当量剂量(organ equivalent dose)用于设定限值以防止确定性效应,有效剂量(effective dose)用于限制和优化对随机效应的防护[1]。由于防护量不能直接测量,需要通过可测量量来进行评估,为此,国际辐射单位与测量委员会(International Commission on Radiation Units and Measurements, ICRU)定义了实用量(operational quantities)。在辐射防护实践中,实用量可用监测仪器测出并作为防护量的合理近似(既不低估也不过高高估)。随着人们对事物认识的深入和科学技术的发展,防护量和实用量相应都发生了变化。2020年ICRU出版了第95号报告[2],该报告提出并详细介绍了新实用量。本文就外照射实用量的发展过程、适用范围、其定义以及计算模体的变化等作了重点回顾和综述,以供相关专业人员参考。
一、实用量的发展过程1971年ICRU在其第19号报告中首次建议将吸收剂量指数和剂量当量指数作为外照射的实用量[3]。同年,在其第20号报告中建议考虑使用受照人体的最大剂量当量(MADE)[4]。ICRU在1985年和1988年分别出版了第39号报告和第43号报告,提出将周围剂量当量、定向剂量当量和个人剂量当量定义为实用量[5-6],并在其第43号报告和第47号报告(1992年)中提供了光子和电子的应用内容[6-7]。1993年,ICRU第51号报告对个人监测量进行了部分修改,将个人剂量当量名称由individual dose equivalent改为personal dose equivalent[8]。ICRU在其第43、47和57号报告(1998年)、ICRP第74号出版物(1996年)中分别公布了从辐射量和剂量学量到这些实用量的转换系数[6-7, 9-10]。2001年,ICRU第66号报告增加了关于中子的内容[11]。2010年,ICRP与ICRU联合发布了ICRP第116号出版物,提供了从注量和空气比释动能到不同粒子类型和能量的防护量的转换系数[12],包括了更大范围粒子类型和粒子能量的转换系数,例如那些仅在宇宙辐射和粒子加速器中出现的粒子,能量范围高达200 GeV;同时,还介绍了ICRP第110号出版物中提供的成年男性和女性参考模体的使用结果[13]。
在近20年来,越来越多的医疗和研究人员以及商业飞行员暴露在比使用现行实用量可测量的更低或更高能量的电离辐射中。而ICRU第39/51号报告的实用量是对发生在核燃料循环、铀处理、核电站以及核废料储存和后处理中的光子(50 keV~3 MeV)和中子(热中子~20 MeV)能量范围内的防护量的可接受估计。它们与防护量的关系很复杂,剂量计校准的转换系数也仅针对光子、中子和电子。现有的实用量局限性逐渐凸显,明显偏离了防护量(或低估或过高高估)。因此,ICRU联合ICRP重新定义了实用量,并在2020年以ICRU第95号报告形式发布。该报告提出了一套与有效剂量和吸收剂量直接相关的实用量,适用于更大范围的粒子(包括光子、电子、正电子、中子、α粒子、μ介子、π介子等),以及不同粒子的能量范围(1 keV~200 GeV)[14],从而更好地估计防护量。
二、定义的变化1. 现有实用量的定义:在ICRU第39/51号报告中把实用量系统地分为用于监测人员的量,即个人剂量当量,和用于监测工作场所或环境中的量,即定向剂量当量和周围剂量当量。剂量当量(H)定义为组织或器官吸收的剂量(D)与品质因子(Q)的乘积:
| $ H=Q \cdot D $ | (1) |
式中,D是在体内或模体指定深度d进行评估的,全身吸收剂量指定深度为10 mm,眼晶状体和局部皮肤则分别为3 mm和0.07 mm;品质因子Q(体现不同辐射生物有效性)是粒子在水中相互作用点处的线性能量传递(LET或L∞)的函数。
防护量的计算分为三步:首先计算人体器官和组织的平均吸收剂量;然后计算器官和组织的当量剂量;最后是有效剂量的计算[1]。由于不同辐射类型在单位吸收剂量引起健康影响方面的有效性不同,在第二步将吸收剂量值乘以辐射权重因子wR,wR代表了计算器官当量剂量时对辐射有效性差异的简化调整。品质因子Q和辐射权重因子wR的目的均是对不同类型辐射赋予一个相对权重,但它们是不能直接进行比较的,因为无论是基于定义还是测量辐射的有效性,它们都是不同的概念。
2. 新实用量的定义:为了解决扩展辐射类型和能量范围需要的问题,同时在这个扩展范围内保持对防护量的良好近似估计,需要改变实用量定义的方式。ICRU第95号报告建议将实用量重新定义为空间点或物体表面的辐射量或剂量,以及使用与防护量值相关的转换系数。这个新定义使用与防护量相同的模体、权重因子和计算模型,从而确保了防护量和实用量的相干性。新的实用量简化了防护量和实用量之间的关系,并更有助于理解防护量。
(1) 周围剂量(ambient dose):辐射场中某点的周围剂量H*定义为该点处的粒子注量Φ与转换系数h*的乘积。对于不同辐照条件,该转换系数将粒子注量与有效剂量的最大值Emax关联在一起。
对于粒子类型为i的能量分布,周围剂量Hi*用下式计算:
| $ H_{i}^{*}=\int h_{i}^{*}\left(E_{\mathrm{p}}\right)\left[\frac{\mathrm{d} \Phi_{i}\left(E_{\mathrm{p}}\right)}{\mathrm{d} E_{\mathrm{p}}}\right] \mathrm{d} E_{\mathrm{p}} $ | (2) |
式中,
(2) 眼晶状体定向吸收剂量(directional absorbed dose in the lens of the eye):在特定入射Ω方向上辐射场中某点处眼晶状体定向吸收剂量D′lens(Ω) 定义为该点处的粒子注量Φ(Ω)和转换系数d′lens(Ω) 的乘积。该转换系数将粒子注量与眼晶状体的吸收剂量关联在一起。
对于粒子类型为i的能量分布,眼晶状体的定向吸收剂量D′lens, i(Ω) 用式(3)计算:
| $ D_{\text {lens, } i}^{\prime} \varOmega=\int d_{\text {lens, } i}^{\prime}\left(E_{\mathrm{p}}, \varOmega\right)\left[\frac{\mathrm{d} \Phi_{i}\left(E_{\mathrm{p}}, \varOmega\right)}{\mathrm{d} E_{\mathrm{p}}}\right] \mathrm{d} E_{\mathrm{p}} $ | (3) |
式中,
(3) 局部皮肤定向吸收剂量(directional absorbed dose in local skin):在特定入射角Ω方向上辐射场中某点处的局部皮肤定向吸收剂量D′ local skin(Ω)定义为该点处粒子注量Φ(Ω)与转换系数d′local skin(Ω)的乘积。该转换系数将粒子注量与局部皮肤的吸收剂量关联在一起。
对于粒子类型为i的能量分布,局部皮肤定向吸收剂量D′locals kin, i(Ω)用式(4)计算:
| $ D_{\text {locals kin, } i}^{\prime}=\int d_{\text {locals kin, } i}^{\prime}\left(E_{\mathrm{p}}, \quad\right)\left[\frac{\mathrm{d} \Phi_{i}\left(E_{\mathrm{p}}, \varOmega\right)}{\mathrm{d} E_{\mathrm{p}}}\right] \mathrm{d} E_{\mathrm{p}} $ | (4) |
式中,
(4) 个人剂量(personal dose):身体上某一点的个人剂量Hp定义为该点处的入射粒子注量Φ和转换系数hp的乘积。该转换系数将粒子注量与有效剂量E的值关联在一起。
对于粒子类型为i的能量及角分布,个人剂量Hp, i用式(5)计算:
| $ H_{\mathrm{p}, i}=\iint h_{\mathrm{p}, i}\left(E_{\mathrm{p}}, \varOmega\right)\left[\frac{d^{2} \Phi_{i}\left(E_{\mathrm{p}}, \right)}{\mathrm{d} E_{\mathrm{p}} d}\right] \mathrm{d} E_{\mathrm{p}} d $ | (5) |
式中,$d^{2} \Phi_{i}\left(E_{\mathrm{p}}, \varOmega\right) / \mathrm{d} E_{\mathrm{p}} \mathrm{d} \varOmega$ 表示在入射角为Ω的附近方向dΩ、在动能Ep附近dEp区间的粒子注量,$h_{\mathrm{p}, i}\left(E_{\mathrm{p}}, \varOmega\right)=$ $E_{i}\left(E_{\mathrm{p}}, \varOmega\right) / \Phi_{i}\left(E_{\mathrm{p}}, \varOmega\right)$,为在入射角为Ω、动能为Ep的给定粒子类型i的转换系数;Hp为全部粒子类型Hp, i的总和,J·kg-1,专用名称是希沃特(Sv)。
(5) 眼晶状体个人吸收剂量(personal absorbed dose in the lens of the eye):头部或身体上某点处的眼晶状体个人吸收剂量Dp lens定义为该点处的入射粒子注量Φ与转换系数dp lens的乘积。该转换系数将粒子注量与眼晶状体吸收剂量关联在一起。
对于粒子类型为i的能量及角分布,眼晶状体个人吸收剂量Dp lens, i用式(6)计算:
| $ D_{\mathrm{p} \text { lens, } i}=\iint d_{\mathrm{p} \text { lens, } i}\left(E_{p}, \right)\left[\frac{\mathrm{d}^{2} \Phi_{i}\left(E_{p}, \varOmega\right)}{\mathrm{d} E_{\mathrm{p}} d}\right] \mathrm{d} E_{p} d $ | (6) |
式中,
(6) 局部皮肤个人吸收剂量(personal absorbed dose in local skin):身体或四肢上某点处的局部皮肤个人吸收剂量Dp local skin定义为该点处的入射粒子注量Φ与转换系数dp local skin的乘积。该转换系数将粒子注量与局部皮肤吸收剂量关联在一起。
对于粒子类型为i的能量及角分布,局部皮肤个人吸收剂量
| $ D_{\mathrm{p} \text { local skin, } i}=\iint d_{\mathrm{p} \text { local skin, } i}\left(E_{\mathrm{p}}, \varOmega\right)\left[\frac{d^{2} \Phi_{i}\left(E_{\mathrm{p}}, \varOmega\right)}{\mathrm{d} E_{\mathrm{p}} d}\right] \mathrm{d} E_{\mathrm{p}} d $ | (7) |
式中,
ICRU第95号报告附录A中详细列出了式(2)~(7)中的转换系数
|
|
表 1 新实用量与现行实用量的对比 Table 1 Comparison between new and existing operational quantities |
三、计算模体的变化
1. 现有实用量使用的计算模体:周围剂量当量H*(10)和定向剂量当量H′(3)、H′(0.07)均是在直径为300 mm的ICRU球上进行定义的。在个人剂量当量当中,Hp(10)所用模体为300 mm×300 mm×150 mm的板状模体;Hp(3)使用的是200 mm×200 mm的圆柱状模体;Hp(0.07)则使用了3种模体,一种是300 mm × 300 mm×150 mm的板状模体,另外两种直径分别为73 mm和19 mm、长度为300 mm的圆柱状模体和棒状模体。这些模体均由ICRU 4元素组织材料制成(密度为1 g·cm-3,由76.2%的氧、11.1%的碳、10.1%的氢和2.6%的氮组成)[15]。
2. 新实用量使用的计算模体
(1) 周围剂量及个人剂量使用的模体:周围剂量和个人剂量使用的计算模体均为全身参考成人模体[13]。全身成人参考模型包括男性和女性计算模型,这些参考计算模型是基于真人计算机断层扫描数据,是人体解剖的数字三维表示[13]。
光子和中子辐射涉及的几何条件有前后(AP)、后前(PA)、左侧(LLAT)、右侧(RLAT)、旋转(ROT)、上半球各向同性(SS-ISO)和下半球各向同性(IS-ISO);电子、正电子、μ介子和π介子辐射涉及的几何条件有AP、PA、PA、ISO、SS-ISO和IS-ISO;He2+离子辐射涉及的几何条件有AP、PA和ISO。更详细的理想化几何条件信息可参阅ICRP第116号出版物。个人剂量计算过程中采用以身体中点为中心的右正交系统。对于给定的Ω,除0°、180°、ROT、ISO、IS-ISO和SS-ISO外,转换系数均为左、右辐射的有效剂量的平均值。
(2) 眼晶状体定向吸收剂量及眼晶状体个人吸收剂量使用的模体:眼晶状体定向吸收剂量和眼晶状体个人吸收剂量使用的模体相同,包括眼睛模体和全身参考成人模体。对于给定入射方向Ω的宽束均匀平行辐射场,取右眼或左眼中吸收剂量的最大值。
(3) 局部皮肤定向吸收剂量及局部皮肤个人吸收剂量使用的模体:在计算局部皮肤定向吸收剂量的转换系数时使用特定的模体,该模体由ICRU 4元素材料组成的300 mm× 300 mm×148 mm组织板(ρ=1.0 g·cm-3,图 1),其前表面覆盖2 mm厚、密度为1.09 g·cm-3的皮肤[13],其元素组成详见ICRP出版物89[16]。吸收剂量在一个直圆柱体的体积上取平均值,该圆柱体深度介于50 μm和100 μm之间,且其轴垂直于模体正面,在板状模体前表面中心下方的横截面积为1 cm2,详见图 1B中圆形深色阴影部分和C中斜向条纹部分。为获得更好的可见性,图 1未按照实际比例绘制,增加了皮肤层的厚度和圆形目标体积的直径。
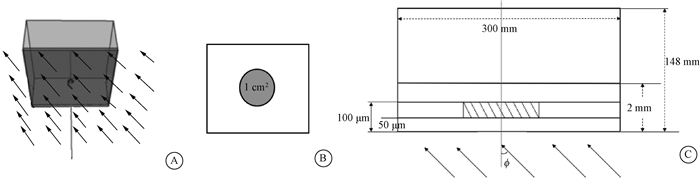
|
图 1 板状模体的几何形状 A.透视图;B.正面图;C.俯视图 Figure 1 Geometry of the slab phantom A. Isometric view; B. View from front; C. View from top |
局部皮肤个人吸收剂量使用的模体具体如下:
① 身体躯干:板状模体,与局部皮肤定向吸收剂量使用的模体相同(图 1)。
② 四肢:圆柱状模体,直径为69 mm、长度为300 mm的ICRU 4元素材料组织(ρ=1.11 g·cm-3),其圆柱表面覆盖有2 mm厚的皮肤。吸收剂量在半径36.4 mm和36.45 mm之间的体积(垂直于圆柱状模体半径)上取平均值,在上下层圆柱表面的圆形投影面积为1 cm2。详见图 2B中斜向条纹部分。为获得更好的可见性,图 2未按照实际比例绘制,增加了皮肤层的厚度和目标体积的直径。
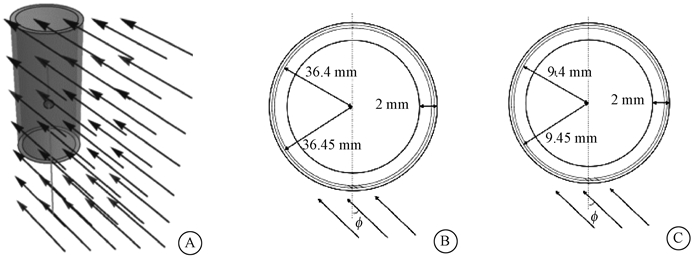
|
图 2 圆柱状/棒状模体几何图形 A. 透视图;B. 圆柱状模体俯视图; C. 棒状模体俯视图 Figure 2 Geometry of the cylindrically shaped phantoms A. Isometric view; B. View from top (pillar phantom); C. View from top (rod phantom) |
③ 手指:棒状模体,直径为15 mm、长度为300 mm的ICRU 4元素材料组织(ρ=1.11 g/cm3),其圆柱表面覆盖有2 mm厚的皮肤。吸收剂量在半径9.4 mm和9.45 mm之间的体积上取平均值,在上下层圆柱表面的圆形投影面积为1 cm2。(详见图 2C中斜向条纹部分)。
相比现行的实用量,新实用量所使用的模体与防护量所使用的模体更为相近。表 2列出了在计算由场所量(注量、空气比释动能)到防护量和新实用量的转换系数所使用模体的对比情况。
|
|
表 2 用于不同部位从场量到防护量和实用量转换系数的模体 Table 2 Phantoms employed to calculate the conversion coefficients from field quantities to protection quantities and operational quantities for different body parts |
四、结语
防护量用于建议职业暴露人员和公众的剂量限制,并优化辐射防护。实用量则通过测量或计算对辐射场进行前瞻性和回顾性评估。ICRU第95号报告提出了一套新的防止外照射的实用量,在相关的转换系数计算中使用了与防护量相同的模体。在ICRP 2021年最新发布的第147号出版物中提出,当量剂量不再作为防护量使用[17]。该出版物认为,为避免皮肤、手脚和眼晶状体的组织反应,使用吸收剂量而不是当量剂量确定限值更为合适。ICRU第95号报告提出的新实用量与ICRP第147号出版物建议的防护量将更为一致。在将这些新的实用量引入辐射防护实践中,则需要重新校准所有的监测器具或剂量计,这些装置的校准程序在很大程度上无需修改,唯一的变化是,校准领域的实用量值需使用在ICRU第95号报告中建议的转换系数。但在某些情况下,也需要重新设计剂量计,例如对能量低于30 keV的光子。新实用量的使用需要逐步和谨慎地采用一段时间,以平衡实施成本和新实用量的好处。
利益冲突 无
作者贡献声明 刘玉连负责论文撰写与修改;刘强、阮书州、王海云指导论文修改;张文艺指导论文设计与修改
| [1] |
International Commission on Radiological Protection. ICRP publication 103. The 2007 recommendations of the International Commission on Radiological Protection[R]. Oxford: Pergamon Press, 2007.
|
| [2] |
International Commission on Radiation Units and Measurements. ICRU report 95. Operational quantities for external radiation exposure[R]. Bethesda: ICRU, 2020.
|
| [3] |
International Commission on Radiation Units and Measurements. ICRU report 19. Radiation quantities and units[R]. Bethesda: ICRU, 1971.
|
| [4] |
International Commission on Radiation Units and Measurements. ICRU report 20. Radiation protection instrumentation and its application[R]. Bethesda: ICRU, 1971.
|
| [5] |
International Commission on Radiation Units and Measurements. ICRU report 39. Determination of dose equivalents resulting from external radiation sources[R]. Bethesda: ICRU, 1985.
|
| [6] |
International Commission on Radiation Units and Measurements. ICRU report 43. Determination of dose equivalents from external radiation sources-part 2[R]. Bethesda: ICRU, 1988.
|
| [7] |
International Commission on Radiation Units and Measurements. ICRU report 47. Measurement of dose equivalents from external photon and electron radiations[R]. Bethesda: ICRU, 1992.
|
| [8] |
Large MJ, Malaroda A, Petasecca M, et al. Modelling ICRP110 adult reference voxel phantoms for dosimetric applications: development of a new Geant4 advanced example[J]. J Phys: Conf Ser, 2020, 1662(1): 012021. DOI:10.1088/1742-6596/1662/1/012021 |
| [9] |
Poludniowski GG. Calculation of X-ray spectra emerging from an X-ray tube. Part Ⅱ. X-ray production and filtration in X-ray targets[J]. Med Phys, 2007, 34(6): 2175-2186. DOI:10.1118/1.2734726 |
| [10] |
Poludniowski GG, Evans PM. Calculation of X-ray spectra emerging from an X-ray tube. Part I. Electron penetration characteristics in X-ray targets[J]. Med Phys, 2007, 34(6): 2164-2174. DOI:10.1118/1.2734725 |
| [11] |
Yap E, Magno LP, Macaraeg CA, et al. Radiation dose in coronary angiography and percutaneous coronary intervention: establishment of diagnostic reference levels at the Philippine Heart Center[J]. Interv Cardiol, 2021, 16: e13. DOI:10.15420/icr.2021.16.PO2 |
| [12] |
Ngaile JE, Msaki PK, Nyanda PB, et al. Estimation of equivalent organ and effective doses to patients undergoing coronary angiography and percutaneous coronary intervention procedures using Monte Carlo simulation[J]. Radiat Phys Chem, 2020, 168(C): 108535. DOI:10.1016/j.radphyschem.2019.108535 |
| [13] |
Buytaert D, Drieghe B, Van Heuverswyn F, et al. Combining optimized image processing with dual axis rotational angiography: toward low-dose invasive coronary angiography[J]. J Am Heart Assoc, 2020, 9(13): e014683. DOI:10.1161/JAHA.119.014683 |
| [14] |
Brambilla M, Cannillo B, Matheoud R, et al. Conversion factors of effective and equivalent organ doses with the air kerma area product in patients undergoing coronary angiography and percutaneous coronary interventions[J]. Phys Med, 2017, 42: 189-196. DOI:10.1016/j.ejmp.2017.09.131 |
| [15] |
朱纯生, 李锋. 急性冠状动脉综合征介入患者辐射剂量分析[J]. 实用医学影像杂志, 2020, 21(1): 11-13. Zhu CS, Li F. Analysis of radiation dose in patients with acute coronary syndrome[J]. J Pract Med Imaging, 2020, 21(1): 11-13. DOI:10.16106/j.cnki.cn14-1281/r.2020.01.004 |
| [16] |
杨博鑫, 李言, 武王将, 等. 心血管介入手术辐射剂量影响因素的分析[J]. 北京生物医学工程, 2019, 38(2): 171-176. Yang BX, Li Y, Wu WJ, et al. Analysis on influence factors of X-ray radiation dose in cardiovascular interventions[J]. Beijing Biomed Eng, 2019, 38(2): 171-176. DOI:10.3969/j.issn.1002-3208.2019.02.009 |
| [17] |
Dabin J, Maeremans J, Berus D, et al. Dosimetry during percutaneous coronary interventions of chronic total occlusions[J]. Radiat Prot Dosim, 2018, 181(2): 120-128. DOI:10.1093/rpd/ncx303 |
| [18] |
Bhar M, Mora S, Kadri O, et al. Monte Carlo study of patient and medical staff radiation exposures during interventional cardiology[J]. Phys Med, 2021, 82: 200-210. DOI:10.1016/j.ejmp.2021.01.065 |
 2022, Vol. 42
2022, Vol. 42


