甲状腺功能亢进(以下简称甲亢)是甲状腺合成或分泌甲状腺激素过多的内分泌疾病，常用治疗方法有抗甲状腺药物治疗(antithyroid drug, ATD)、放射性碘(¹³¹I)治疗和甲状腺切除术。¹³¹I治疗格雷夫斯甲亢指南(2021版)^[1]对3种治疗方法的优劣进行了总结，¹³¹I治疗甲亢相比于手术、ATD，其优势在于操作便捷；控制甲亢症状所需时间短；避免抗甲状腺药物的不良反应；复发比例低。其劣势在于¹³¹I治疗为破坏性治疗，甲状腺功能减低出现后不可逆；部分患者会出现突眼症状加重。甲状腺疾病的¹³¹I疗法于80年前推出^[2-3]，目前临床常以固定公式计算结合医师经验性用药的方法确定甲亢患者¹³¹I用药剂量，该方法存在个体放射敏感性不明确无法量化^[4]，潜在的混杂因素^[5]干扰等，目前尚无明确的指标用以直接预测¹³¹I治疗的结果。神经网络起源于Rosenblatt提出的感知机模型^[6]，目前研究主要集中在深度学习领域，如卷积神经网络架构^[7]，Goodfellow等^[8]提出的生成对抗网络等，已在数据预测、图象处理、语音识别等方向起到越来越重要的作用^[9-13]。神经网络以人的大脑工作模式为基础，从模拟人脑单个神经元功能出发处理信息^[14]，预测变量之间的复杂关系，是传统统计学模型不能做到的^[13]，在临床医学有了较为广泛的应用，如诊断帕金森病^[15]、肝纤维化^[16]、心肌梗死等^[17]，也有研究对甲亢疾病的诊断进行有效分析^[18-20]，但关于¹³¹I治疗方案与给药剂量的预测则少有研究。因此本文提出了预测¹³¹I甲亢核素治疗给药剂量的神经网络模型。依据甲亢临床医学研究，筛选出了有效指标，通过矩阵实验室(matrix laboratory，MATLAB)平台对其构建神经网络模型，对¹³¹I核素治疗甲亢的给药剂量进行预测。

1.临床资料：从上海市多家医院核医学科收集¹³¹I治疗甲状腺的400例病例及其血液检查报告，其中男性157例，女243例，年龄33~68岁，平均年龄45.7岁；患者的全部信息资料, 包括基本情况[如甲状腺重量(thyroid weight，TW)，血清游离三碘甲状腺原氨酸(free triiodothyronine, FT3)、血清游离甲状腺素(free thyroxine, FT4)、促甲状腺激素(thyroid stimulating hormone, TSH)、心率(hate rate, HR)等]、疾病特征、病理特点、治疗及预后等，均来自各家医院信息中心病案管理系统。

2.数据处理：直接搜集到的病例数据包括年龄、病程、甲状腺肿大程度、摄碘率、甲状腺质量等15项指标，使用任意抽样法选取10例病例基本信息以供参考，如表 1所示。

表 1(Table 1)

表 1 病例基本信息 Table 1 Basic information of cases 编号 性别 年龄(岁) 病程 甲状腺肿大程度 HR(min-1) 眼征 手足震颤 TSH(uU/ml) FT3(pmol/L) FT4(pmol/L) 3 h摄碘率(%) 24 h摄碘率(%) TW(g) 给药剂量(×102 MBq) 结局 1 男 54 5个月 Ⅱ 96 + + 0.00 46.08 73.03 65.46 63.56 50 2.96 复发 2 男 36 2个月 Ⅱ 106 + + 0.01 17.98 47.08 79.39 76.43 50 2.96 治愈 3 男 27 1个月 I+ 96 + + 0.01 7.69 30.73 53.69 63.54 45 3.33 甲减 4 男 66 6个月 I 114 - + 0.01 21.31 67.53 59.87 79.00 35 2.22 无效 5 女 53 2年 I+ 84 - + 0.02 9.39 26.83 53.29 79.06 45 2.59 甲减 6 男 18 6个月 I 78 - + 0.03 11.33 28.37 66.5 90.74 40 1.67 甲减 7 女 47 1年 I+ 72 + - 0.01 7.10 23.36 39.64 47.30 40 3.70 甲减 8 女 36 3年 Ⅱ+ 90 + + 0.01 39.16 78.56 92.61 97.86 55 2.04 疗效不佳 9 女 36 2年 Ⅱ 84 - + 0.00 16.61 42.93 26.54 44.31 45 4.44 甲减 10 女 57 11年 I+ 78 + - 0.02 5.22 29.35 22.06 28.36 30 4.81 疗效不佳 注：HR. 心率；TSH. 促甲状腺激素；FT3. 游离三碘甲状腺原氨酸；FT4. 游离甲状腺素；TW. 甲状腺重量

表 1 病例基本信息 Table 1 Basic information of cases

根据美国甲状腺协会(American Thyroid Association, ATA)2016年版诊疗指南内容^[21]，患者在接受¹³¹I治疗后甲状腺功能恢复正常和甲状腺功能减低均认为治疗成功，因此本研究认为结局“好转”与“甲减”为有效给药剂量，共308例，并根据临床经验对病例指标进行初步筛选，选定TW、HR、FT3、FT4、TSH为有效指标。为避免神经网络在训练过程中耗时过长，同时减小预测误差，对数据进行了归一化处理，通过使用MATLAB的mapminmax语句，将输入数据归一到[0, 1]区间。

3.模型选择

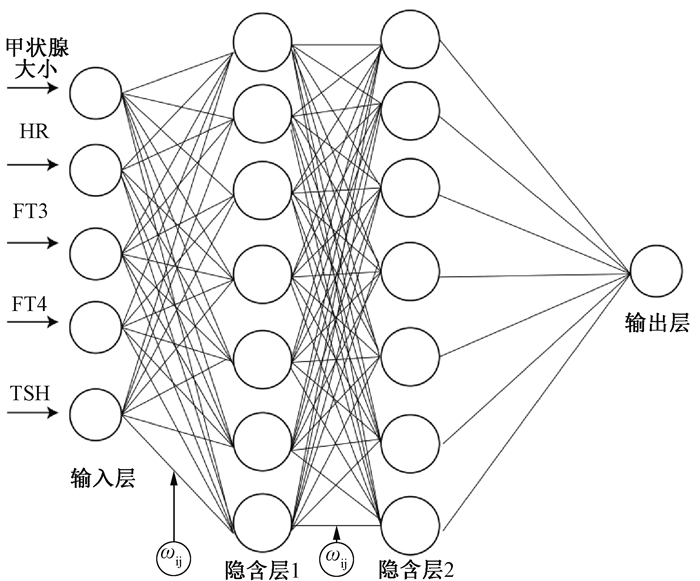
(1) 反向传播(back propagation，BP)神经网络：BP神经网络的原理是基于误差反向传播^[22-23]，能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程，对于非线性回归预测问题是非常有效的工具^[24]。其由输入层、隐含层、输出层组成，信息通过输入层输入模型，经隐含层处理，从输出层输出^[23]。虽然在足够样本数量下，理论上多次训练的单隐含层网络可以逼近任何有理函数^{[22, 25]}，但对于多输入的复杂样本，可以使用多隐含层减小预测误差^[26]。本文所使用结构为5-7-7-1的神经网络模型拓扑结构如图 1所示，其中ω_ij表示神经网络连接的权值。使用MATLAB的newff语句建立神经网络，训练次数设为100，学习率设定为0.005，采用trainlm函数训练。

图 1 BP神经网络结构示意图 Figure 1 Schematic diagram of BP neural network

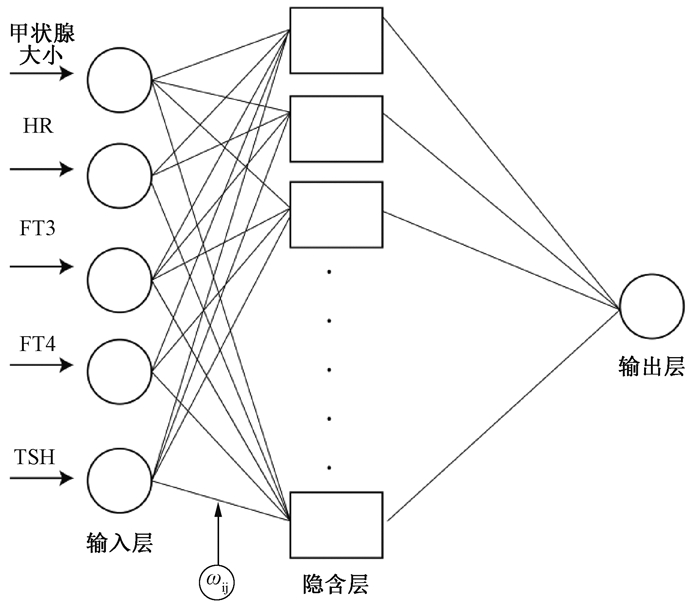
(2) 径向基(radial basis function，RBF)神经网络：RBF网络结构简单、收敛快速，并且拥有优秀的推广能力，在预测分析领域有广泛运用^[27-28]，其主要原理是通过径向基函数对输入矢量进行变换，使其在高维空间内线性可分。其为3层前向神经网络，第一层为输入层；第二层为隐含层，其激活函数为对中心点径向对称且衰减的非负非线性函数；第三层为输出层。本文选用的网络结构如图 2所示^[23]。使用newrb语句建立神经网络，径向基函数的扩展速度设为0.09。

图 2 RBF神经网络结构示意图 Figure 2 Schematic diagram of RBF neural network

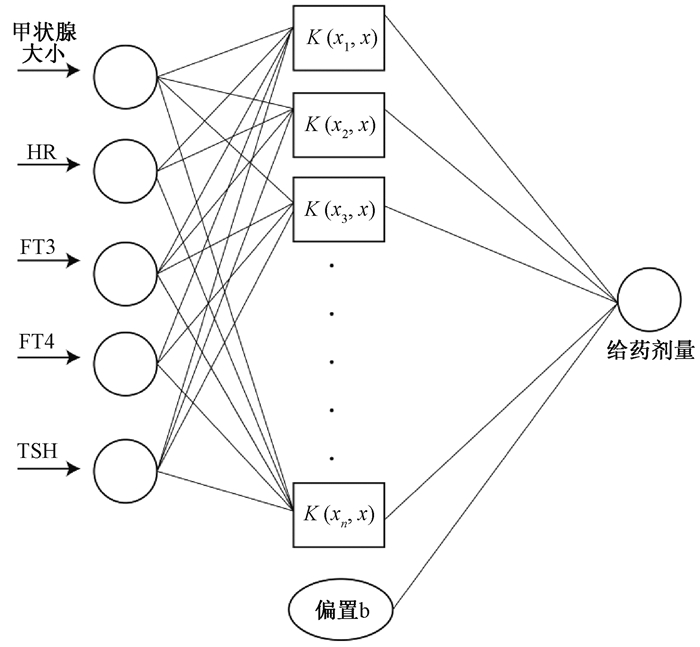
(3) 支持向量机(support vector machine, SVM)：SVM方法兼顾训练误差和泛化能力，对于非线性、高维数、局部极小值问题中表现出许多特有的优势^[29]，其主要思想是建立一个分类超平面作为决策曲面，使得正例和反例之间的隔离边缘被最大化，结构如图 3所示^{[23, 30]}，其中K(x_i, x)表示其核函数。近几年来基于SVM的回归预测已经在电力^[31]、天气^[32]领域中有所应用，并且今年来也有研究将其用于医学领域^[33-34]，因此本研究基于LIBSVM工具箱^[35]，建立¹³¹I给药剂量模型，采用交叉验证方法确定SVM的输入参数，c=20.76，g=0.017，p=0.12。

图 3 SVM结构示意图 Figure 3 Schematic diagram of SVM

1.模型对比：为了分析不同算法的预测效果，首先以简单随机抽样法选取100组样本作为训练集，从剩余的样本中再次简单随机抽样选取10组作为测试集，对其预测的结果进行比较。为了保证样本抽取的随机性，本研究使用MATLAB的randperm语句，将308组有效样本随机排列，选取前一百组作为训练集，第101至110组作为测试集。BP神经网络、RBF神经网络、SVM模型对同一测试集预测的平均误差分别为5.53%、7.09%、9.64%，其具体结果如表 2所示。

表 2(Table 2)

表 2 3种不同模型在同一测试集下给药活度的预测结果(×102 MBq) Table 2 Predicted results of three different algorithms under the same parameter(×102 MBq) TW(g) 给药活度 给药活度-BP 给药活度-SVM 给药活度-RBF 60 3.70 3.10 3.19 3.25 45 4.07 3.94 4.35 3.70 43 3.15 3.26 3.08 3.29 25 3.74 3.84 3.21 3.66 41 2.96 2.74 3.00 3.64 35. 2.55 2.52 2.39 2.30 35 2.33 2.16 2.23 2.28 50 2.96 2.83 2.89 3.65 42 3.70 3.54 3.83 3.87 45 3.33 3.16 3.74 3.13 注：给药活度-BP. BP神经网络预测值; 给药活度-SVM. SVM预测值; 给药活度-RBF. RBF神经网络预测值

表 2 3种不同模型在同一测试集下给药活度的预测结果(×102 MBq) Table 2 Predicted results of three different algorithms under the same parameter(×102 MBq)

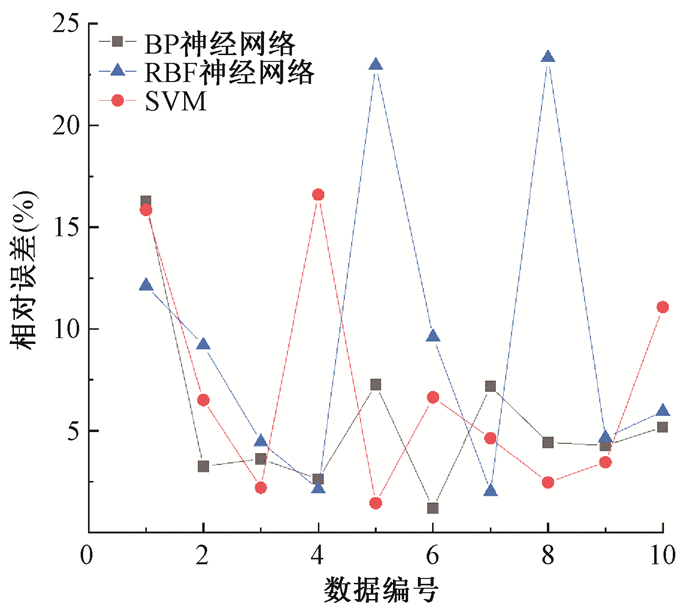
图 4显示了3种模型的验证相对误差，我们建立的3种模型的预测值和临床数据值很接近，预测的能力很好，在这15组验证数据中，大部分偏差在10%以内，预测值精度良好，总体上达到了模型应用的需要。可以看出BP网络较RBF神经网络与SVM在预测精度上有更大的优势，综上最终选择BP网络进行预测。

图 4 3种不同预测模型基于同一验证集的相对误差 Figure 4 Relative errors in three different neural network models based on the same verification set

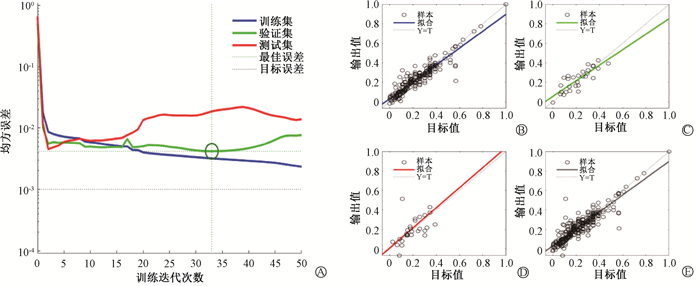
2.BP神经网络训练：BP神经网络整体训练过程如图 5所示，数据由MATLAB分为“训练集(Training)”、“验证集(Validation)”、“测试集(Test)”互不交叉的3部分，“Training”是用来训练网络的样本，“Validation”是调试某些参数的样本，“Test”是检验拟合效果的样本；“目标值(Goal)”由net.trainParam.goal参数设置，该参数表示预期的最小误差；“最优值(Best)”是训练后实际获得的误差精度^[24]。由图 5可以看出在迭代1~5次时，测试网络的误差快速下降，但随着训练的进行，迭代次数的增加，网络误差趋势逐渐平缓；当迭代次数在33次以后，出现最佳；训练集、验证集、测试集及总样本再训练的拟合效果中，R值分别为0.93、0.84、0.59、0.89。R值越接近1，说明模型拟合效果越好，可以看出本模型有较好的预测回归能力。

图 5 网络训练过程  A. 训练过程中均方误差变化；B.训练集拟合效果; C.验证集拟合效果; D.测试集拟合效果; E.总样本拟合效果 Figure 5 Process of network training   A. Change in mean square error during training; B. Fitting results of Training; C. Fitting results of Validation; D. Fitting results of Test; E. Fitting results of total sample

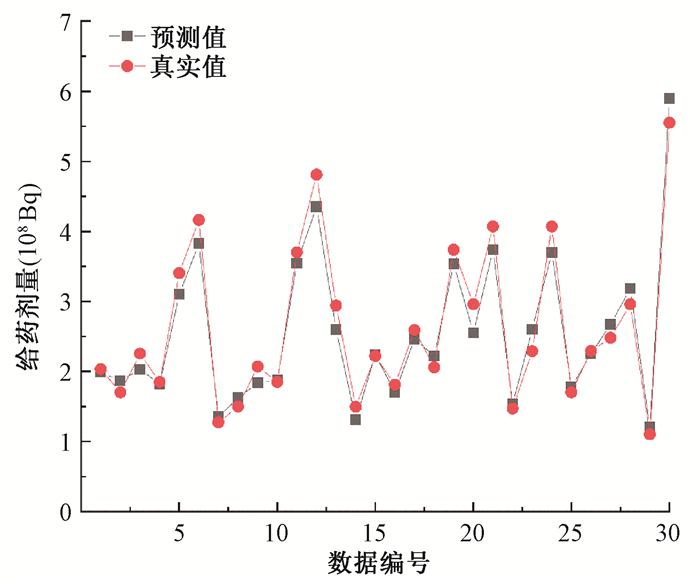
3.数据验证：通过临床数据对该BP神经网络模型的输出结果进行验证，本研究训练集与测试集按1∶9划分，即选取总样本量的十分之一(30组数据)进行验证，输出值与临床数据对比结果如表 3和图 4所示(表 3篇幅所限仅展示10组数据)，其预测结果的平均误差为7.22%，均方误差为0.053，最大误差为13.78%。由图 6可知预测数据与验证数据极为接近，可认为该模型实现了血检指标、甲状腺质量、HR与给药剂量映射关系的描述，可在一定程度上进行¹³¹I剂量值的预测。

表 3(Table 3)

表 3 BP网络模型预测值与实际值对比 Table 3 Comparisons of predicted values and actual values for BP network 甲状腺质量(g) 实际给药活度(MBq) 单位质量给药活度真实值(MBq/g) 预测给药活度(MBq) 单位质量给药活度预测值(MBq/g) 误差(%) 48 204 4.27 199 4.17 2.41 27 222 8.33 224 8.41 0.93 37 181 4.89 170 4.59 6.16 35 259 7.40 247 7.05 4.77 38 206 5.46 222 5.88 7.68 19 127 6.60 135 7.02 6.39 24 150 6.29 162 6.81 8.29 27 229 8.46 225 8.31 1.80 47 185 3.97 188 4.03 1.42 25 185 7.27 182 7.17 1.50

表 3 BP网络模型预测值与实际值对比 Table 3 Comparisons of predicted values and actual values for BP network

图 6 神经网络预测值与真实值对比 Figure 6 Comparisons of predicted values and actual values for of neural network

如何确定甲亢患者¹³¹I最佳给药剂量一直是甲亢治疗的难题，目前用于临床计算甲亢患者¹³¹I给药剂量的计算公式过于简单，难以实现个性化治疗^[36]。本研究提出了基于人工智能的方法，根据患者的临床表现、检验结果、病史病程等数据实现¹³¹I给药剂量的预测。本研究样本的数据从多家医院收集，来源广泛，年龄与病程跨度大，涵盖了甲亢病程的各个阶段，样本具有代表性，通过比较BP神经网络、RBF神经网络、SVM的预测效果，发现BP神经网络相较于另外两个模型计算结果误差最小，稳定性好，因此，最终选定BP神经网络作为预测模型。

本文提出的甲亢核素治疗预测模型仅仅是一次尝试，研究过程还存在一定的不足，主要包括：模型的选取上只使用了3种简单的机器学习算法，并没有使用更为复杂的算法进行模型训练，方法学上可以进一步优化与丰富，提高预测结果的精度；目前可收集的样本数据为400例，若纳入更多甲亢数据进行模型训练，可进一步提升模型预测结果的准确性。

此外，目前纳入模型训练的部分参数主观性过强，例如甲状腺肿大程度的判定由就诊医师根据临床经验进行判定，病史采集以患者自述为主，此类数据主观性强，在模拟过程中这些数据不可避免地会给计算结果带来一定误差；所有甲亢数据均以最后一次随访结果作为本模型预测的结局进行计算，并不能说明未来患者完全没有复发可能，预测模型真正是否具有实际意义需要还大量临床实践数据的支持，仅以回顾性数据进行计算缺乏说服力。因此，本模型还需要进一步以未来临床应用结果来验证本文所建立模型计算结果是否可信。

本研究的目的为医生对甲亢患者进行放射性碘治疗时提供剂量参考，以甲状腺功能恢复正常为最优，尽可能降低或推迟甲状腺功能减低的发生，避免复发的可能。经过训练后本模型拥有较好的准确度，基本可以实现给药剂量的预测，相比于传统公式法操作更加简便，并且随着样本量的增加准确率还能进一步提升，这使得神经网络法在大数据的时代更具潜力^[37]，满足患者、工作人员及公众对于放射防护的需求。

在本预测模型的基础上进行衍生，其余条件不变的前提下将结局作为输入值，给药剂量作为输出值，某种程度上可作为评估个体放射敏感性的指标，该工作需要更多数据及理论的支撑，这些问题是下一步研究的重点。

利益冲突  本文由署名作者按以下贡献声明独立开展，不涉及各相关方的利益冲突

作者贡献声明  袁炜烨负责模型训练、论文撰写；姚杰负责数据整理分析和论文修改；蒋舟、肖虹、白江涛负责信息调查、数据录入整理、分析等；钱爱君、王彬负责组织协调科研进展；高林峰指导论文设计与撰写