中华放射医学与防护杂志  2022, Vol. 42 Issue (12): 966-972   PDF    
引用本文
易金玲, 杨继明, 雷希瑶, 宁博达, 金献测, 张吉. 基于计划复杂度参数利用机器学习预测容积弧形调强验证通过率研究[J]. 中华放射医学与防护杂志, 2022, 42(12): 966-972, DOI: 10.3760/cma.j.cn112271-20220812-00331.
基于计划复杂度参数利用机器学习预测容积弧形调强验证通过率研究
易金玲1 , 杨继明2 , 雷希瑶1 , 宁博达1 , 金献测1 , 张吉1     
1. 温州医科大学附属第一医院放疗中心，温州 325000;
2. 宁波市第一医院放化疗中心, 宁波 315000
收稿日期: 2022-08-12
基金项目: 温州市科技局(Y2020917, ZY2022016)
通信作者: Zhang ji, Email: jizhang1996@126.com
[摘要] 目的 采用随机森林和支持向量机两种机器学习算法建立预测模型，实现容积弧形调强(VMAT)验证γ通过率(GPR)的数值预测和分类预测。方法 回顾性选取2019年4月至2020年8月于温州医科大学附属第一医院放疗中心接受VMAT放疗的258例患者资料，其中头颈部38例，胸腹部220例。对所有患者VMAT计划提取13个复杂度参数，收集计划验证在3%/3 mm和2%/2 mm评估标准下的GPR。用随机种子数方法将患者队列分为70%训练队列和30%验证队列，采用随机森林和最小冗余最大相关性(mRMR)的方法分别筛选数值预测和分类预测的相关性参数，利用随机森林和支持向量机两种算法结合计划靶区(PTV)体积，子野宽度，平滑度因素分别建立复杂度模型和混合模型。分析比较两种模型的预测性能。结果 对GPR数值预测，在3%/3 mm、2%/2 mm评估标准下，验证队列中基于随机森林和支持向量机复杂度模型预测误差的均方根误差(RMSE)和平均绝对误差(MAE)分别为1.788%和1.753%、5.895%和5.444%、1.415%和1.334%、4.644%和4.255%；基于随机森林和支持向量机的混合模型预测误差的RMSE和MAE分别为1.760%和1.815%、5.693%和5.590%、1.386%和1.319%、4.523%和4.310%。GPR分类预测中，在3%/3 mm、2%/2 mm评估标准下，验证队列中基于随机森林和支持向量机的复杂度模型的受试者工作特征(ROC)曲线下面积(AUC)分别为0.790和0.793、0.763和0.754；在验证队列中基于随机森林和支持向量机的混合模型的AUC结果分别为0.806和0.859、0.796和0.796。结论 开发了基于随机森林方法和支持向量机方法的复杂度模型和混合预测模型，能够实现在3%/3 mm和2%/2 mm两种评估标准下对VMAT放疗计划GPR的数值预测和分类预测，混合模型较经典复杂度模型提高了预测精度。
[关键词] 容积弧形调强    质量保证    随机森林算法    预测模型    
Predicting passing rate for VMAT validation using machine learning based on plan complexity parameters
Yi Jinling1 , Yang Jiming2 , Lei Xiyao1 , Ning Boda1 , Jin Xiance1 , Zhang Ji1     
1. Radiotherapy Center, the 1st Affiliated Hospital of Wenzhou Medical University, Wenzhou 325000, China;
2. Radiotherapy and Chemotherapy Center, Ningbo First Hospital, Ningbo 315000, China
Fund programs: Wenzhou Science and Technology Bureau (Y2020917, ZY202216)
[Abstract] Objective To establishaprediction model using the random forest (RF) and support vector machine (SVM) algorithms to achieve the numerical and classification predictions of the gamma passing rate (GPR) for volumetric arc intensity modulation (VMAT) validation. Methods Atotal of 258 patients who received VMAT radiotherapy in the 1st Affiliated Hospital of Wenzhou Medical University from April 2019 to August 2020 were retrospectively selected for patient-specific QA measurements, including 38 patients who received VMAT radiotherapy for head and neck, and 220 patients who received VMAT radiotherapy for chest and abdomen. Thirteen complexity parameters were extracted from the patient′s VMAT plans and the GPRs for VMAT validation under the analysis criteria of 3%/3 mm and 2%/2 mm were collected. The patients were randomly divided into a training cohort (70%) and a validation cohort (30%), and the complexity parameters for the numerical and classification predictions were screened using the RF and minimum redundancy maximum correlation (mRMR) method, respectively. Complexity models and mixed models were established using PTV volume, subfield width, and smoothness factors based on the RF and SVM algorithms individually. The prediction performance of the established models was analyzed and compared. Results For the validation cohort, the GPR numerical prediction errors of the complexity models based on RF and SVM under the two analysis criteria are as follows. The root-mean-square errors (RMSEs) under the analysis criterion of 3%/3 mm were 1.788% and 1.753%, respectively; the RMSEs under the analysis criterion of 2%/2 mm were 5.895% and 5.444%, respectively; the mean absolute errors (MAEs) under the analysis criterion of 3%/3 mm were 1.415% and 1.334%, respectively, and the MAEs under the analysis criteria of 2%/2 mm were 4.644% and 4.255%, respectively. For the validation cohort, the GPR numerical prediction errors of the mixed models based on RF and SVM under the two analysis criteria were as follows. The RMSEs under the analysis criterion of 3%/3 mm were 1.760% and 1.815%, respectively; the RMSEs under the analysis criterion of 2%/2 mm were 5.693% and 5.590%, respectively; the MAEs under the analysis criterion of 3%/3 mm were 1.386% and 1.319%, respectively, and the MAEs under the analysis criteria of 2%/2 mm were 4.523% and 4.310, respectively. For the validation cohort, the AUC result of the GPR classification prediction of the complexity models based on RF and SVM were 0.790 and 0.793, respectively under the analysis criterion of 3%/3 mm and were 0.763 and 0.754, respectively under the analysis criterion of 2%/2 mm. For the validation cohort, the AUC result of the GPR classification prediction of the mixed models based on RF and SVM were 0.806 and 0.859, respectively under the analysis criterion of 3%/3 mm and were 0.796 and 0.796, respectively under the analysis criterion of 2%/2 mm cohort. Conclusions Complexity models and mixed models were developed based on the RF and SVM method. Both types of models allow for the numerical and classification predictions of the GPRs of VMAT radiotherapy plans under analysis criteria of 3%/3 mm and 2%/2 mm. The mixed models have higher prediction accuracy than the complexity models.
[Key words] VMAT    Quality assurance    Random forest algorithm    Prediction model    

容积弧形调强(VMAT)作为一种新型调强放疗技术，不同于固定野调强放疗，VMAT能够在机架旋转的同时，通过改变剂量率、多叶准直器位置以及机架转速等参数实现束流强度调制，不仅能够产生更均匀的靶区剂量分布和更低的正常组织受量，还具有更高的治疗效率，是目前国内外广泛应用的肿瘤放疗技术[1-3]。然而，调强放疗的计划和执行都非常复杂，为了确保投递到患者体内放疗剂量的准确性，在治疗实施前对放疗计划进行患者特定质量保证(QA)即剂量验证程序是必要的安全测试[4-5]。我国目前放疗人员/设备配置水平较发达国家仍有较大差距，传统的调强剂量验证通常需要物理师在一天的治疗工作结束后将验证模体置于加速器下模拟患者治疗出束，得到模体实测剂量分布，并对计划的通过率进行分析，该过程耗时、费力且增加了机器损耗[6]。另一方面，对于验证未通过的调强计划，可能需要重新设计放疗计划并再次验证，延长了患者的等待时间从而可能导致额外的医疗风险[7]。近年来，机器学习(ML)在医学物理领域的应用受到了高度关注，尤其在放疗质量控制和保证的应用方面，许多研究报道了ML方法能够用于剂量验证的预测研究，该方法的应用显著降低了QA的工作量，将QA从劳动密集转向技术密集型工作，有利于不同放疗中心QA水平的同质化发展[8-10]。本研究收集258例VMAT调强放疗计划，提取计划复杂度参数、靶区体积、子野宽度以及通量平滑度等因素，采用随机森林和支持向量机两种机器学习方法建立QA验证通过率预测模型，并对3%/3 mm和2%/2 mm两种不同评估标准下的γ通过率(GPR)进行数值和分类预测。

资料与方法

1. 一般资料：回顾性选取2019年4月至2020年8月于温州医科大学附属第一医院放疗中心进行VMAT治疗的258例患者资料，其中头颈部患者38例，胸腹部患者220例，年龄27~87岁，中位年龄57岁。患者均采用仰卧位、热塑体模固定。直线加速器型号为Synergy(瑞典Elekta公司)，配备了40对MLCi2TM型多叶准直器，所有计划均采用6 MV X射线束。所有放疗计划均在MONACO V5.1.1版本(瑞典Elekta公司)治疗计划系统上完成，射野参数采用双弧，控制点间隔为1.5，计算网格为0.3 cm，不确定度为1%，剂量沉积方式选择Dm(dose to medium)。所有的计划均进行了患者特异性QA测量。

2. 剂量验证：放疗计划进行传统的模体测量验证。使用ArcCHECK三维二极管矩阵(美国Sun Nuclear公司)在直线加速器下模拟患者摆位，并调用计划模拟患者治疗出束，通过率分析采用配套的SNC Patient软件V6.7版(美国Sun Nuclear公司)，剂量阈值预设为10%，采用3%/3 mm和2%/2 mm两个γ标准进行剂量分布比较。本研究中，3%/3 mm标准下γ通过率在95%以下的被视为不通过，95%及以上为通过；2%/2 mm标准下，γ通过率在80%以下的被视为不通过，80%及以上为通过。

3. 计划参数和复杂度参数：用MATLAB V2010a (美国Mathwork公司)的House-built软件，读取和处理VMAT计划输出的DICOM-RT文件中的信息，包括治疗计划信息、组织结构(靶区和危及器官)、计划剂量分布等。运行自行编写的程序代码，得到VMAT的机器跳数(MU)、控制点数(CPs)、每个子野/控制点的调制复杂度评分[MCSv/Beam(Arc)]、平均子野面积(SA(cm2)/CP)等13个复杂度参数[11-12]，具体复杂度参数见表 1。

表 1 计划参数和复杂度参数在训练队列和验证队列中患者的特征(x±s) Table 1 Characteristics of the plan parameters and complexity parameters of patients in the training and validation cohort (x±s)

4. 经典复杂度模型的构建和评估：本研究基于随机森林和支持向量机两种机器学习算法来构建数值预测模型和分类预测模型。采用随机种子数将患者队列分为7∶3的训练队列和验证队列。数值预测中，采用随机森林算法在训练队列中进行5次十折交叉验证，获得复杂度参数个数与平均预测误差之间的关系，建立随机森林模型获得复杂度参数的重要性程度排名，选取合适数量的复杂度参数分别构建基于随机森林和支持向量机算法的数值预测模型。分类预测中，采用mRMR的特征筛选方法，比较不同复杂度参数数量下的模型在验证队列中的性能，选取合适的复杂度参数数量分别构建基于随机森林和支持向量机算法的分类预测模型。针对GPR数值预测准确性，平均值(x)、标准差(s)、均方根误差(root mean squard error, RMSE)和平均绝对误差(mean absolute error, MAE) 作为评价指标；对于GPR分类预测准确性，绘制受试者工作特征(ROC)曲线，使用曲线下面积(AUC)进行评价。

5. 混合模型的构建和评估：PTV体积，子野宽度，平滑度这3个计划参数也被考虑在本研究中。在经典复杂度模型的基础上，将PTV体积，子野宽度，平滑度3个计划参数分别加入经典数值预测模型和分类预测模型，得到相应的混合模型。针对GPR数值预测准确性，x、s、RMSE和MAE作为评价指标；对于GPR分类预测准确性，绘制受试者ROC曲线，使用AUC进行评价。

6. 统计学处理：本研究复杂度参数筛选以及建立的随机森林模型和支持向量机模型基于R语言(Version 4.2.0)实现。在数值预测中，随机森林模型树的数量设置为500，类型设置为regression，其余参数选择默认设置；支持向量机模型的cost和gamma值在一定阈值范围内选择训练队列的最佳值，类型设置为eps-regression，其余参数选择默认设置。在分类预测中，随机森林模型树的数量设置为500，类型设置为classification，其余参数选择默认设置；支持向量机模型的cost和gamma值在一定阈值范围内选择训练队列的最佳值，类型设置为C-classification，核函数设置为polynomial，其余参数选择默认设置。mRMR的特征筛选方法采用mRMRe包实现；随机森林模型的构建采用randomForest包实现；支持向量机模型的构建采用e1071包实现；ROC曲线的实现采用pROC包。

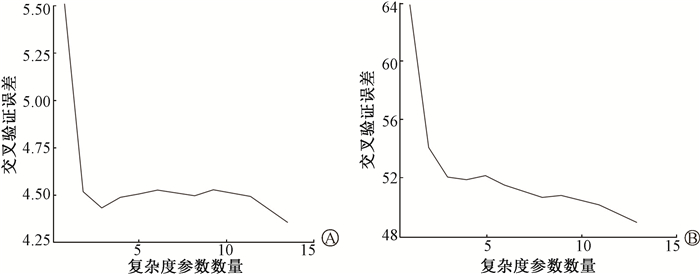
结果

1. GPR数值预测：训练队列180例VMAT计划，其中3%/3 mm标准下GPR≥95%的有159例，< 95%的有21例；2%/2 mm标准下GPR≥80%的有145例，< 80%的有35例。验证队列78例，其中3%/3 mm标准下GPR≥95%的有71例，< 95%的有7例；2%/2 mm标准下GPR≥80%的有70例，< 80%的有8例。训练队列中平滑度为无，低和中的患者分别有8，4和168例；验证队列中平滑度为无，低和中的患者分别有3，3和72例。如图 1所示，在3%/3 mm和2%/2 mm条件下，均选择13个复杂度参数能够使交叉验证的平均误差达到最小。

图 1 不同标准数值预测的复杂度参数数量与交叉验证误差的示意图A. 3%/3 mm；B. 2%/2mm Figure 1 Schematic representations of the complexity parameter quantity vs. cross-validation errors for the numerical prediction under different criteria A. 3%/3 mm; B. 2%/2mm

不同标准下，评估分析标准越严格，验证队列预测的数值偏差越大，详见表 2。

表 2 GPR数值和分类预测在不同标准下验证队列中的结果 Table 2 Numerical and classification prediction results of the GPR under different criteria for the validation cohort

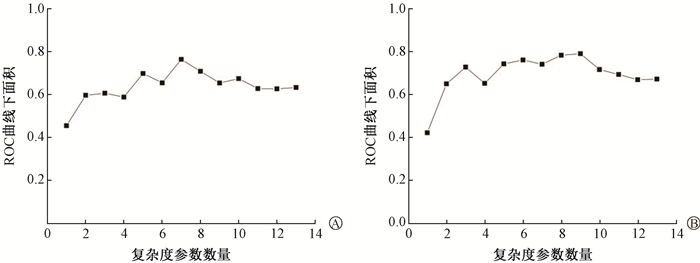
2. GPR分类预测：如图 2所示，在3%/3 mm和2%/2 mm评估标准下，分别选择7个和9个复杂度参数能够使验证队列的ROC曲线下面积达到最大。在3%/3 mm评估标准下，选择了CPs，MCSv/Beam(Arc)，%MU/CP < 3，%MU/CP < 2，SA(cm2)/CP，LT(mm/Arc)和LS(mS/Arc)。在2%/2 mm评估标准下，选择了Dose，CPs，MCSv/Beam(Arc)，GantrySpacing，%MU/CP < 3，%MU/CP < 2，SA(cm2)/CP，LT(mm/Arc)和LS(mS/Arc)。将选择的复杂度参数与PTV体积，子野宽度，平滑度结合建立混合模型。

注：ROC. 受试者工作特征 图 2 不同标准分类预测的ROC曲线下面积与复杂度参数数量之间的关系A. 3%/3 mm；B. 2%/2mm Figure 2 Relationships between the area under the roc curve and the quantity of complexity parameters for classification prediction under different criteria A. 3%/3mm; B. 2%/2mm

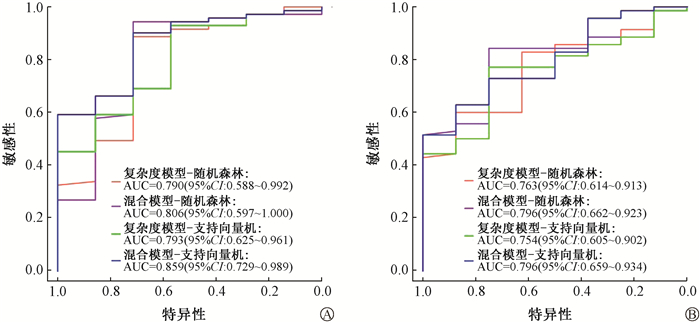
如图 3所示，在3%/3 mm评估标准下，基于随机森林和支持向量机的复杂度模型在验证队列中的结果分别为0.790和0.793；混合模型在验证队列的结果分别0.806和0.859。在2%/2 mm评估标准下，基于随机森林和支持向量机的复杂度模型在验证队列中的结果分别为0.763和0.754；混合模型在验证队列中的结果分别0.796和0.796，详见表 2。

注：ROC. 受试者工作特征 图 3 不同评估标准下验证队列中的随机森林和支持向量机的复杂度模型和混合模型ROC曲线A. 3%/3mm；B. 2%/2mm Figure 3 The roc curves of the complexity models and mixed models based on random forest and support vector machine under different criteria for the validation cohort A. 3%/3mm; B. 2%/2mm

讨论

现代调强放疗能够实现“剂量雕刻”，而越是复杂的剂量越是需要精准的执行[13]。现阶段针对患者调强放疗计划的剂量验证工作需要在直线加速器下，使用模体或其他验证设备对其放疗计划进行测量并分析，并确保该项工作在计划执行前完成，如何准确高效地完成该过程是目前亟待解决的问题[5]。先前的研究表明剂量的准确性与计划的复杂程度有关，Shen等[11]利用经典相关分析法分析了VMAT放疗计划复杂度，证明了计划质量和可传输性之间的相关性。Granville等[14]构建了线性支持向量分类器(support vector classifier，SVC)，将放疗计划特征和直线加速器性能指标作为模型的输入端，对VMAT QA结果进行了分类预测来观察计划和测量剂量之间的中位剂量差(±1%)是否在范围内，然而该研究并没有使用临床上最常使用的GPR。Ono等[15]利用600例VMAT计划的复杂度参数、机器类型和光子束能量等28个变量，应用机器学习算法建立预测模型，分别对剂量偏差5%、3%/3 mm标准下GPR进行预测，该方法仅仅针对3%/3 mm标准，在临床应用上受到了一定的限制。

最近的研究表明，从放疗计划提取的复杂度参数与患者的GPR具有相关性，于此同时一些学者使用特定复杂度参数作为预测因子预测患者的GPR获得了不错的效果。Tomori等[16]报告了孔径复杂性对VMAT的影响，开发了孔径正则化函数，以提高VMAT计划的剂量传递精度；其他学者发现调强放射治疗中的子野大小影响患者特定QA通过率[17]，这些研究表明，基于复杂度参数的调强计划剂量验证是可行的。在本研究中，从放疗计划中提取的13个复杂度参数，其中CPs，MCSv/Beam(Arc)，%MU/CP＜3，%MU/CP＜2，SA(cm2)/CP，LT(mm/Arc)，LS(mS/Arc)在分类预测中的3%/3 mm和2%/2 mm两种不同评估标准下均被选择，MCSv/Beam(Arc)通常用于表征计划的复杂性。

运用机器学习的方法预测GPR的准确性已经发展成为一种比传统更有效的质量保证方法[16-18]。本研究中收集头颈部，胸部等多部位的调强放疗计划，提取相应的复杂度参数并结合了PTV体积，子野宽度，平滑度几种因素，采用两种机器学习算法建立了基于复杂度参数的模型和基于复杂度参数结合PTV体积，子野宽度，平滑度的混合模型分别预测3%/3 mm和2%/2 mm两种不同评估标准下的GPR数值与分类的准确性。

本研究中在数值预测方面，3%/3 mm评估标准下的验证队列中基于随机森林和支持向量机的复杂度模型预测误差的x±s分别为0.415%±1.751%和0.167%±1.774%；混合模型预测误差的x±s分别为0.412%±1.730%和0.006%±1.827%。2%/2 mm评估标准下的验证队列中基于随机森林和支持向量机的复杂度模型预测误差的x±s分别为1.852%±5.633%和0.922 %±5.480%；混合模型预测误差的x±s分别为1.784%±5.441%和1.169%±5.502%。这与Ono等[15]的研究结果相近，在他们的研究中基于回归树分析、多元回归分析和神经网络3种机器学习模型对GPR的预测误差分别为0.6%±2.4%、0.5%±2.4% 和0.2%±2.1%。本研究结果表明，评估标准越严格，数值预测的偏差越大，这与Li等[19]报道的3%/3 mm、3%/2 mm和2%/2 mm标准下的平均预测误差分别为1.81%、2.39% 和4.18%的结果相似。本研究向复杂度模型加入PTV体积，子野宽度，平滑度三个因素能够提高数值预测的精度。樊林等[20]的研究报道了伽马通过率与靶区PTV体积相关，邱刚等[21]的研究表明通量平滑度不同等级的选择影响着剂量分布。在分类预测方面，3%/3 mm评估标准下的验证队列中基于随机森林和支持向量机的复杂度模型的AUC值，敏感性和特异性分别为0.790、0.887、0.714和0.793、0.930、0.571；混合模型的AUC值，敏感性和特异性分别为0.806、0.944、0.714和0.859、0.901、0.714。2%/2 mm评估标准下的验证队列中基于随机森林和支持向量机的复杂度模型的AUC值，敏感性和特异性分别为0.763、0.600、0.875和0.754、0.771、0.750；混合模型的AUC值，敏感性和特异性分别为0.796、0.843、0.750和0.796、1.000、0.514。研究结果表明，混合模型的分类预测精度要优于单纯复杂度模型，结合不同类型的特征可以改进预测精度。Hirashima等[22]使用复杂度指标、放射组学特征和临床参数混合特征训练基于树的ML模型，研究也表明使用混合特征集可以提高模型的准确性。

本研究尚且存在一些局限性。首先，本研究未根据肿瘤类型建立亚组分析，治疗部位可能对GRP的预测有一定的影响。其次，本研究中的复杂度参数尽管包含了已被证明与GPR相关的复杂度参数，但更多更深层次的复杂度参数和机器参数并没有被考虑到。再次，目前预测模型只涉及二维剂量分析，针对三维剂量差异缺乏有效的方法，本团队正致力于研究结合计划复杂度参数和三维剂量分布等更多的剂量信息，利用ML/深度学习(DL)研究自动QA方法来预测GPR以及三维个体剂量差异。最后，由于不同放疗机构的直线加速器、计划系统及测量设备客观上存在差异，本研究中的预测模型仅仅基于本中心的数据，因此在未来的研究还需要多个中心的数据对模型进行进一步验证，以提高模型的实际应用效果。如何克服不同机构不同机器设备对剂量预测模型的影响，也是所关注的方向。

综上所述，本研究开发了一种基于随机森林和支持向量机的机器学习方法的混合模型，能够实现在3%/3 mm和2%/2 mm两种评估标准下对GPR的数值预测和分类预测，与经典的复杂度模型相比，进一步提高了预测的准确性。这项研究为质量保证提供了一种新的方法，提高了放疗中心的工作效率，缩短了患者等待放疗的时间，有助于今后开发更有效和更简便的患者QA方法，避免和减少了繁琐的实际测量过程。

利益冲突  无

作者贡献声明  易金玲负责论文选题、数据收集和文章起草；杨继明负责文献查阅和文章修改；雷希瑶、宁博达负责资料收集和文献查找；金献测负责技术支持、论文修改；张吉负责论文撰写和数据分析

参考文献
[1]
田源, 张红志. 肿瘤放射治疗技术进展[J]. 中华结直肠疾病(电子杂志), 2016, 5(4): 287-291.
Tian Y, Zhang HZ. Advances of technology in radiation oncology[J]. Chin J Colorec Dis(Electron Ed), 2016, 5(4): 287-291. DOI:10.3877/cma.j.issn.2095-3224.2016.04.002
[2]
张矛, 金海国, 杨金磊, 等. 容积旋转调强与固定野调强计划在鼻咽癌放疗中的剂量学比较[J]. 中华放射医学与防护杂志, 2014, 34(11): 852-854.
Zhang M, Jin HG, Yang JL, et al. Dosimetric comparison between volume rotation intensity modulation and fixed field intensity modulation in radiotherapy for nasopharyngeal carcinoma[J]. Chin J Radiol Med Prot, 2014, 34(11): 852-854. DOI:10.3760/cma.j.issn.0254-5098.2014.11.013
[3]
Chiavassa S, Bessieres I, Edouard M, et al. Complexity metrics for IMRT and VMAT plans: a review of current literature and applications[J]. Br J Radiol, 2019, 92(1102): 20190270. DOI:10.1259/bjr.20190270
[4]
LoSasso T, Chui CS, Ling CC. Comprehensive quality assurance for the delivery of intensity modulated radiotherapy with a multileaf collimator used in the dynamic mode[J]. Med Phys, 2001, 28(11): 2209-2219. DOI:10.1118/1.1410123
[5]
Ezzell GA, Burmeister JW, Dogan N, et al. IMRT commissioning: multiple institution planning and dosimetry comparisons, a report from AAPM Task Group 119[J]. Med Phys, 2009, 36(11): 5359-5373. DOI:10.1118/1.3238104
[6]
张烨, 易俊林, 姜威, 等. 2019年中国大陆地区放疗人员和设备基本情况调查研究[J]. 中国肿瘤, 2020, 29(5): 321-326.
Zhang Y, Yi JL, Jiang W, et al. Survey on the basic information of personnel and facilities of radiotherapy in Chinese mainland in 2019[J]. China Cancer, 2020, 29(5): 321-326. DOI:10.11735/j.issn.1004-0242.2020.05.A001
[7]
钟秋子, 李晔雄. 乳腺癌保乳术后放疗延迟对预后影响[J]. 中华放射肿瘤学杂志, 2015, 24(3): 354-357.
Zhong QZ, Li YX. Prognostic effect of delayed radiotherapy after breast conserving surgery[J]. Chin J Radiat Oncol, 2015, 24(3): 354-357. DOI:10.3760/cma.j.issn.1004-4221.2015.03.031
[8]
Osman A, Maalej NM. Applications of machine and deep learning to patient-specific IMRT/VMAT quality assurance[J]. J Appl Clin Med Phys, 2021, 22(9): 20-36. DOI:10.1002/acm2.13375
[9]
Valdes G, Chan MF, Lim SB, et al. IMRT QA using machine learning: A multi-institutional validation[J]. J Appl Clin Med Phys, 2017, 18(5): 279-284. DOI:10.1002/acm2.12161
[10]
Chan MF, Witztum A, Valdes G. Integration of AI and machine learning in radiotherapy QA[J]. Front Artif Intell, 2020, 3: 577620. DOI:10.3389/frai.2020.577620
[11]
Shen L, Chen S, Zhu X, et al. Multidimensional correlation among plan complexity, quality and deliverability parameters for volumetric-modulated arc therapy using canonical correlation analysis[J]. J Radiat Res, 2018, 59(2): 207-215. DOI:10.1093/jrr/rrx100
[12]
Otto K. Volumetric modulated arc therapy: IMRT in a single gantry arc[J]. Med Phys, 2008, 35(1): 310-317. DOI:10.1118/1.2818738
[13]
Miften M, Olch A, Mihailidis D, et al. Tolerance limits and methodologies for IMRT measurement-based verification QA: Recommendations of AAPM Task Group No. 218[J]. Med Phys, 2018, 45(4): e53-e83. DOI:10.1002/mp.12810
[14]
Granville DA, Sutherland JG, Belec JG, et al. Predicting VMAT patient-specific QA results using a support vector classifier trained on treatment plan characteristics and linac QC metrics[J]. Phys Med Biol, 2019, 64(9): 095017. DOI:10.1088/1361-6560/ab142e
[15]
Ono T, Hirashima H, Iramina H, et al. Prediction of dosimetric accuracy for VMAT plans using plan complexity parameters via machine learning[J]. Med Phys, 2019, 46(9): 3823-3832. DOI:10.1002/mp.13669
[16]
Tomori S, Kadoya N, Takayama Y, et al. A deep learning-based prediction model for gamma evaluation in patient-specific quality assurance[J]. Med Phys, 2018. DOI:10.1002/mp.13112
[17]
Shiba E, Saito A, Furumi M, et al. Predictive gamma passing rate by dose uncertainty potential accumulation model[J]. Med Phys, 2019, 46(2): 999-1005. DOI:10.1002/mp.13333
[18]
Valdes G, Scheuermann R, Hung CY, et al. A mathematical framework for virtual IMRT QA using machine learning[J]. Med Phys, 2016, 43(7): 4323. DOI:10.1118/1.4953835
[19]
Li J, Wang L, Zhang X, et al. Machine learning for patient-specific quality assurance of VMAT: prediction and classification accuracy[J]. Int J Radiat Oncol Biol Phys, 2019, 105(4): 893-902. DOI:10.1016/j.ijrobp.2019.07.049
[20]
樊林, 唐斌, 赵艳群, 等. 靶区体积与调强验证伽马通过率关系研究[J]. 陕西医学杂志, 2016, 45(3): 316-318.
Fan L, Tang B, Zhao YQ, et al. Study on the relationship between the volume of target area and the gamma passing rate of intensity modulation verification[J]. Shaanxi Med J, 2016, 45(3): 316-318. DOI:10.3969/j.issn.1000-7377.2016.03.022
[21]
邱刚, 房保栓, 魏强, 等. 通量平滑度对宫颈癌放射治疗的剂量学影响[J]. 中国辐射卫生, 2021, 30(3): 288-294.
Qiu G, Fang BS, Wei Q, et al. Impact of fluence smoothing on the dosimetry of cervical cancer radiotherapy[J]. Chin J Radiol Health, 2021, 30(3): 288-294. DOI:10.13491/j.issn.1004-714X.2021.03.008
[22]
Hirashima H, Ono T, Nakamura M, et al. Improvement of prediction and classification performance for gamma passing rate by using plan complexity and dosiomics features[J]. Radiother Oncol, 2020, 153: 250-257. DOI:10.1016/j.radonc.2020.07.031