放射治疗对治疗时体位精度要求很高,胸腹部肿瘤靶区由于体位固定效果欠缺,且易受呼吸心跳、器官运动及充盈状态变化和摆位偏差的影响[1-2],从而在治疗过程中肿瘤位置和形状发生变化,导致剂量覆盖不足而降低放疗效果[3],但增加靶区外扩又会带来更多的周围组织射线暴露[4-6]。因此,放疗过程中的肿瘤位置跟踪具有很大意义。射波刀(CyberKnife)等实时影像引导设备利用X射线透视成像跟踪法实现术中肿瘤实时成像[7],但需要植入金属标记物,造成二次创伤且会引入额外辐射剂量[8-9],且对于肺部的靶区植入标记会带来肺穿孔风险[10-11]。另外,体外标志、光学体表等利用体外信号关联体内肿瘤运动的方法也被提出[12-13]。体外和体内信号非线性相关且存在滞后性[14],患者个体化差异和异常呼吸的问题也需要解决。利用治疗兆伏级(MV)射线及配套的电子射野影像系统(EPID)获取治疗影像并进行肿瘤位置跟踪,具有无标记、无延时、不需额外设备且无额外辐射剂量的优点,但同时存在以下3个方面的问题:MV图像的高噪声水平和低对比度[15];多叶准直器(MLC)遮挡导致肿瘤图像不完整;治疗过程中肿瘤的非刚性变形[16]。肿瘤跟踪问题可以转为计划影像和治疗影像配准和偏差分析的问题。利用计划射束方向观(BEV)图像与治疗EPID影像进行配准,可计算治疗过程中靶区位置和形状变化,为治疗验证、剂量评估和动态MLC治疗等提供参考。传统配准方法基于图像强度度量优化变形场,每次配准进行大计算量的参数优化调整,很难做到实时化[17]。机器学习可通过共享通用网络参数实现高效、稳健的配准,擅长于处理非线性、信息缺失情况[18]。Voxelmorph为端到端无监督网络非刚性配准算法,采用相似性测度驱动图像变形,其速度快且不需标注,本研究选用其作为肿瘤跟踪算法的核心框架,用以应对低质量、MLC遮挡和存在形变的MV图像处理的问题。
资料与方法1. 病例资料:本研究以模体数据验证算法的准确性,并收集患者数据以提供实际临床治疗中肿瘤运动的量化结果。所有定位CT图像层厚5 mm,采用荷兰飞利浦公司24排大孔径螺旋CT获取模体和病例数据。将定位图像传至MONACO(version 5.11.03)计划系统进行靶区勾画、计划设计和剂量计算。所有计划采用容积旋转调强放射治疗(VMAT),射线能量为6 MV,通过搭载Agility机头160叶MLC(叶片在等中心治疗平面投影宽度0.5 cm)的瑞典医科达Synergy直线加速器实施。使用直加配套的EPID收集治疗过程中的影像,其采集方式为电影曝光模式,采集频率433.24 ms/帧。图像以1 024×1 024分辨率的16位灰度图形式存储于iView(version 3.4)影像系统。
验证模体的型号为Model 008A, 其组织当量为50 keV~15 MeV。模体内部包含球形靶区、肺等效组织和脊柱,其CT密度值范围与患者相似,骨500~1 000 HU,肺-780~830 HU,肿瘤0~25 HU。将肺部肿瘤的VMAT计划以质量保证(QA)方式移植到模体中并在加速器上执行,且每次在模体的床左右、升降和进出方向手动随机设置了治疗偏移(-1~1 cm),共收集了10次治疗过程中的EPID图像682幅作为固定图像。另外,在计划系统中收集了对应每个固定图像的射野角度的数字影像重建(DRR)图作为浮动图像,进行配准研究。
选取中山大学附属第一医院放疗科的21例肺部肿瘤的VMAT计划作为病例数据。所有患者采用真空袋头先进仰卧体位固定,以病例的计划靶区(PTV)作为靶区研究对象。其中,部分患者体内有多个靶区和计划,所有病例靶区位置分布和数量为:肺左上叶4例,肺左下叶4例,肺右上叶6例,肺中叶22,肺右下叶5个。影像收集方法与上述模体一致,将EPID和对应射野角度的DRR视作待分析图像对,共获取了533对病例图像对进行研究。
2. 跟踪算法
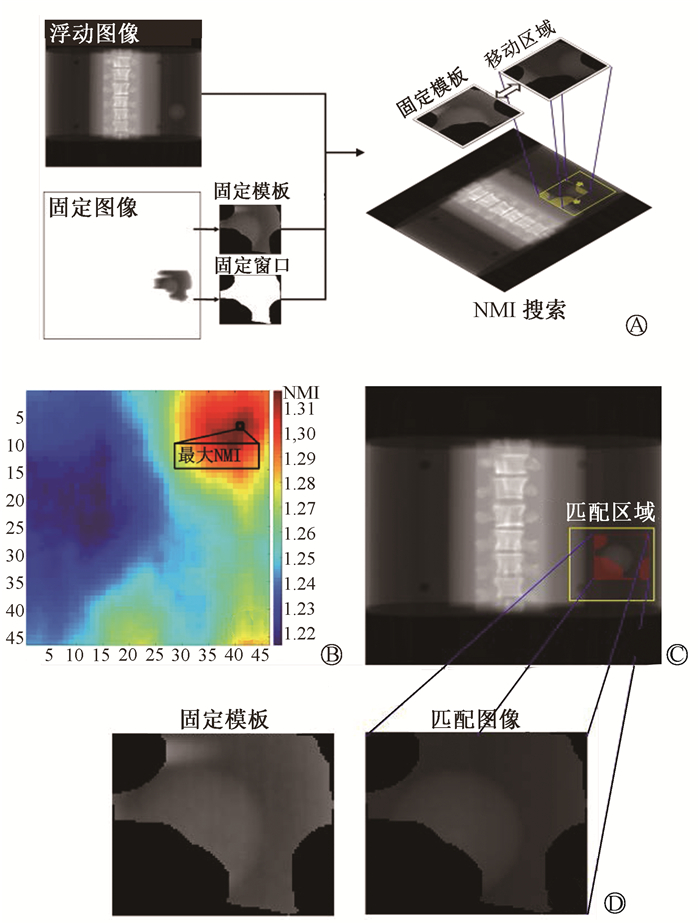
(1) 初步仿射对齐:采用高斯滤波可去除MV图像部分噪声。初步仿射对齐用来消除配对EPID和DRR图像可能存在较大位置差别。另外EPID对于DRR而言相当于将射野外区域数据缺失的图像,本研究采用窗口模板匹配法实现初始对齐。如图 1所示,截取EPID有图像区域生成模板图像,随后根据灰度差生成搜索窗口。将该窗口在DRR图像中与EPID模板图像位置对应的邻域(图 1的黄框)上平移截取图像并与模板图像进行相似度比较。其中相似度最大的截图被认为是匹配图像研究采用标准化互信息(NMI)进行图像相似度的度量。对于图像I,定义其图像熵为:
| $ H(I)=-\sum\limits_{i=0}^{N-1} p_i \log p_i $ | (1) |
|
图 1 初步仿射匹配示意图 A. 模板图像和搜索窗口的生成;B. 最大的NMI对应的区域;C、D.匹配区域和匹配图像 Figure 1 Schematic diagram of the window template matching process in the initial affine alignment A. The generation of the fixed template and search window; B. The region corresponding to the maximum NMI; Cand D. The matched region and matched image |
式中,pi为图像I中灰度i的概率,N代表灰度级数。对于图像对R和F,其联合熵为:
| $ H(R, F)=-\sum\limits_{x, y}{p}(x, y)\log p(x, y) $ | (2) |
式中,x和y分别为图像R和F中的灰度,而p(x, y)为灰度对出现的联合概率。则定义图像R和F的NMI为:
| $ N M I(R, F)=\frac{H(R)+H(F)}{H(R, F)} $ | (3) |
最大的NMI对应的区域被认为是匹配区域(图 1)。将DRR图像根据两个区域的位移差进行平移,即可实现初始仿射对齐。
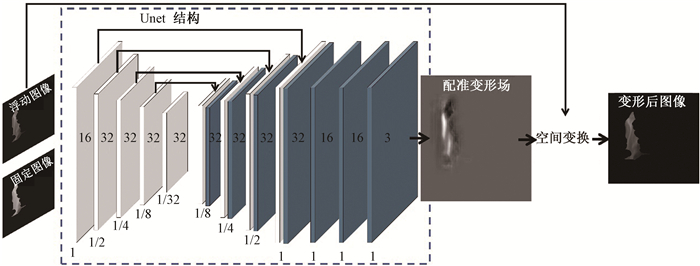
(2) Voxelmorph网络结构:Voxelmorph是基于Unet架构实现图像配准的无监督学习网络[19]。如图 2所示,固定图像fixed image和浮动图像moving image通过一个卷积神经网络生成形变场,并通过空间变换网络(space transformation network,STN)作用于浮动图像缩小其与固定图像之间的差别,最后输出与固定图像更相似的形变图像moved image。
|
图 2 Voxelmorph的网络结构示意图 Figure 2 Schematic diagram of the network structure of Voxelmorph |
网络使用平滑损失函数Lsmooth对形变场ϕ进行约束保证了ϕ的平滑性。并使用相似性损失函数Lsim衡量图像相似性变形的方向。总的损失函数Ltotal可以表示为:
| $ L_{\text {total }}(f, m, \phi)=L_{\text {sim }}\left(f, m^{\circ} \phi\right)+\lambda L_{\text {smooth }}(\phi) $ | (4) |
式中,m°为图像的形变操作,λ为损失函数的权重。相似性损失Lsim在单模态图像处理时选为像素均方误差(MSE),多模态时选为图像局部互相关系数(NCC)。
(3) 非刚性配准模型的训练和测试:非刚性配准模型的处理对象为初始对齐后DRR和EPID射野内的图像,其原因如下:射野图像包含部分或全部肿瘤区域,而射野外图像配准无临床意义;只有射野内区域接收X射线,与剂量直接相关;EPID射野外的区域图像数据缺失会干扰配准结果。模体数据集和病例数据集被分开进行训练和验证。
以初始配准后的EPID为固定图像fixed image,DRR为浮动图像moving image。将所有图像对按0.7∶0.3的比例分为训练集数据和测试集数据。选择Adam(adaptive moment estimation)作为模型训练的优化器。考虑MV和kV图像的成像能量不同导致的灰度和亮度差异,相似性函数选用NCC,其定义如下:
| $ \begin{align} & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ NCC(f, m, \phi )=\sum\limits_{p\in \Omega } \\ & \frac{\sum_{{{p}_{i}}}{\left( f\left( {{p}_{i}} \right)-\hat{f}(p) \right)}\cdot \left( [m\circ \phi ]\left( {{p}_{i}} \right)-[\hat{m}\circ \phi ](p) \right)}{\sqrt{\sum_{{{p}_{i}}}{{{\left( f\left( {{p}_{i}} \right)-\hat{f}(p) \right)}^{2}}}\cdot \sum_{{{p}_{i}}}{{{\left( [m\circ \phi ]\left( {{p}_{i}} \right)-[\hat{m}\circ \phi ](p) \right)}^{2}}}}} \\ \end{align} $ | (5) |
式中,f(pi) 和
3. 结果评估:对于模体数据,因肿瘤模拟小球CT值与周围组织有明显差别,不管在EPID还是DRR图像上都有明显圆形边界。即使受MLC遮挡图像缺失,也可以根据其圆形状将边界补充完整。本研究采用手动勾画的方式定义了小球的边界,通过比较这些边界的质心变化,可以得到误差较小的偏移测量值。在方向定义上,本研究取BEV图左右方向的偏移为Dx,上下方向为Dy(对应治疗头脚方向)。则模体中跟踪算法的误差可以用欧氏距离ED定义为:
| $ E D=\sqrt[2]{\left(D_{x r}-D_{x g}\right)^2+\left(D_{y r}-D_{y g}\right)^2} $ | (6) |
式中,Dxr、Dxg分别为投影图左右方向的配准、实际的偏移;Dyr、Dyg分别为上下方向上配准、实际的偏移。根据该定义,ED为两个方向上偏移的综合误差,其值越小表示跟踪效果越好。
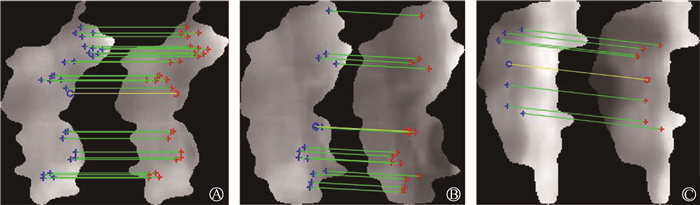
对于病例数据,由于其靶区形状不规则,无法用直接勾画方式进行结果评估。研究采用射野内图像特征提取匹配法来衡量靶区质心的偏移。如图 3所示,使用最小特征值法[20]检测出配准前EPID图像的特征点(图 3中的蓝色十字标记),而配准后的图像的对应特征点(图 3中的红色十字标记)采用KLT(Kanade-Lucas-Tomasi)跟踪算法识别[21-22]。则配准前后靶区质心位移可由这些特征点的平均质心(图 3中的蓝色和红色圆圈标记)的位置差表示,将其定义为患者靶区的欧式距离ED:
| $ E D_{ {patient }}=\sqrt[2]{\left.\left(D_{x a}-D_{x b}\right)^2+D_{y a}-D_{y b}\right)^2} $ | (7) |
|
注:蓝色十字为配准前EPID图像特征点;红色十字为配准后图像对应特征点;蓝色、红色O为特征点的平均质心 图 3 病例数据靶区质心偏移的测量示意图 A. 示例1;B. 示例2;C. 示例3 Figure 3 Schematic diagram of target volume offset in patient data A. Example 1; B. Example 2; C. Example 3 |
式中,Dxb、Dyb为配准前的靶区特征点平均质心坐标;Dxa、Dya为配准后靶区特征点平均质心坐标。
此外,分析了配准前后EPID和DRR射野内图像的相似度(以NMI为度量指标)作为第三方验证。
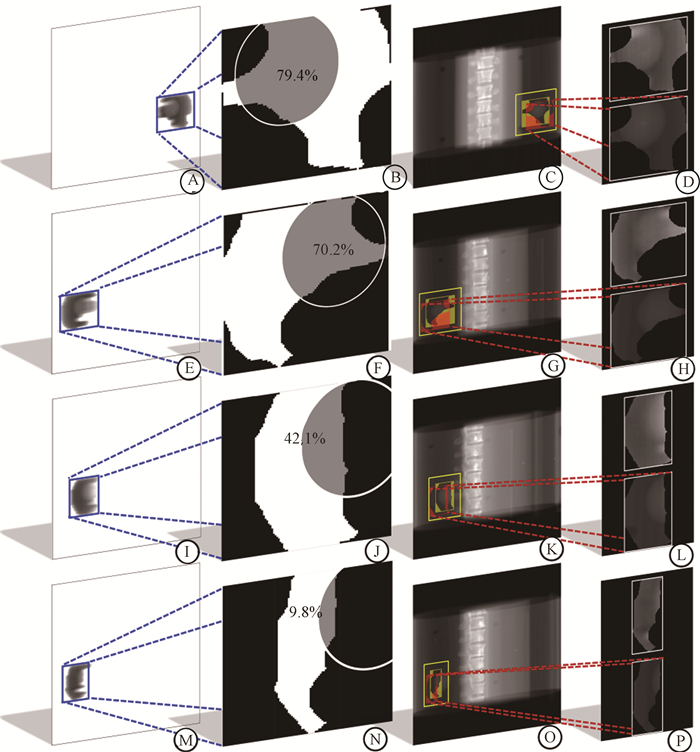
结果1. 初步仿射配准:本研究中fixed window生成时设定的灰度阈值为200,大于该阈值的区域定义为射野外区域(如图 3所示)。窗口的内缩参数为10个像素,搜索邻域定义为固定窗口周围各外扩50个像素,搜索步长为1个像素。由于模体验证试验中手动设置了治疗偏移,且射野内因MLC叶片遮挡,模体肿瘤模拟小球在EPID射野图像中会出现不同程度的数据缺失。图 4呈现了各种程度的缺失情况及匹配效果,其中缺失程度用射野内的小球面积占其总面积表示。模体数据配准失败数90(包括肉眼上看出明显失败、射野过小无法确定小球位置或ED结果>1的情况),成功率占模体总图像样本(682对)的86.80%。病例数据配准失败数64,成功率占病例总图像样本(533对)的88.00%。图像孔径大小对匹配的效果影响最大,而在调强计划(调强适形放射治疗IMRT和VMAT)通常采用窄束传输以得到平滑精细的剂量分布效果,可以看到本算法对较小射野孔径的数据缺失情况也具有鲁棒性。
|
A、E、I、M. EPID图像;B、F、J、N. 跟踪算法可处理10%~80%的缺失情况;C、G、K、O. DRR图像中匹配区域;D、H、L、P. C、G、K、O配准结果 图 4 不同缺失程度图像的匹配效果 A, E, I, M. EPID images; B, F, J, N. The tracking algorithm handling images with 10%-80% of data missing; C, G, K, O. Matched regions in DRR images; D, H, L, P. Obtained satisfactory alignment results Figure 4 Initial alignment of images with varying degrees of data missing |
2. Voxelmorph的模型训练及非刚性配准的验证:在模型训练中,设置epoch=3,step=10,batchsize=1,其他参数用默认。总的训练迭代次数为1.1万次。在模体数据中,训练集数据和验证集数据分别为475对和207对图像,训练结果NCC损失为-0.03;病例数据中,训练集373对图像,验证集160对图像,训练结果NCC损失为-0.03。
为了验证该网络模型在图像非刚性形变中的表现性能,本研究采用手动设置变形的方式进行测试。因模体中肿瘤模拟物的形状简单且临床意义不大,变形实验基于病例数据进行。在EPID射野内的图像中模拟了实际临床治疗中患者的骨骼、肺轮廓和肺阴影区域的形变。图 5中可以看到原始的DRR图像跟随EPID的形变效果进行非刚性变换并表现出较好的配准效果。变形场主要应用于形变相差较大的区域。

|
注:A、E、I跟随EPID的形变效果进行非刚性变换,并表现出C、G、K红色框内较好的配准效果;B、F、J红色框内变形分别模拟了实际临床治疗中病人的骨骼、肺轮廓和肺阴影区域的形变 A、E、I. DRR图像;C、G、K. 红色框内较好的配准效果;D、H、L. 对应的变形场;B、F、J. EPID图像 图 5 Voxelmorph模型非刚性配准效果 A, E, I. DRR images; C, G, K. Encouraging registration results in red boxes; D, H, L. Corresponding deformation fields; B, F, J. EPID images Figure 5 Non-rigid registration results using a Voxelmorph model |
3. 跟踪算法的模体验证结果:对于模体的共面VMAT计划,因治疗中心点位于模体中心,而肿瘤模拟小球位于模体偏侧。因此在治疗过程的BEV图中,小球计划位置和实际位置跟随射野角度变化出现周期性重叠分离,导致x方向上的偏移出现周期波动,而y方向上不明显。由结果可知,配准偏移与实际偏移较接近,在Dx方向偏差 < 2.5 mm,Dy方向上 < 2 mm。
模体验证结果中,大部分ED在 < 3 mm的范围内(86.80%),而 < 2 mm的ED约为80.0%,最大ED可接近12 mm。此外ED较大的案例在控制点上具有集中分布的特点,主要位于20,40,60和90左右控制点附近。在图像相似性测度中,配准前后射野内的NMI变化为1.18 ± 0.02到1.20 ± 0.02(t=-6.78,P=0.001)。
4. 跟踪算法在病例数据中的结果:配准前后病例数据中的靶区偏移测量如表 1所示。可以发现治疗过程中的肿瘤运动以平移为主,且在Dx和Dy方向上的偏移范围接近(-5.27 ~5.27 mm)。而Dy方向(对应于肺的头脚方向)平均位移较大(2.68 ± 1.75)mm,与临床情况一致。而两个方向的综合位移反应了治疗过程中靶区的的偏移,其平均值为3.78 mm,最大可达7.46 mm。其中上肺的ED偏移范围为0~4.55 mm,下肺的偏移范围为0~7.46 mm。在配准前后EPID和DRR的射野图像相似性测度中,NMI变化为1.21 ± 0.03到1.22 ± 0.03(t=-2.91,P=0.001)。而图像显示配准存在相对较小但不可以忽视的非刚性形变。
|
|
表 1 配准前后患者靶区变化的评估(mm, x±s) Table 1 Evaluation of offset in the patient′s target volumes before and after registration (mm, x±s) |
讨论
本研究提出一种基于Voxelmorph端对端无监督机器学习网络,可应对低图像质量、MLC遮挡和非刚性形变的MV图像的无标记肿瘤跟踪算法。该算法利用BEV图和EPID图的配准,获取治疗过程中靶区相对计划的运动和形变。若该形变超过设定治疗阈值可进行报警实现治疗验证;其次模型使用了治疗过程中实时获取的EPID数据,反映了真实的辐射野区域,可为实际剂量评估提供参考;另外,靶区的位移和形变结果也可为动态MLC治疗的辐射野形状调整提供依据。本研究使用模体数据验证了算法的可靠性,并将该算法应用于病例数据,对治疗过程中的患者肿瘤位移给出一个量化的结果。该算法对不同放疗技术具有通用性,无创且不需增加设备和引入额外辐射,具有实时肿瘤监测的可能性。
Cui等[23]和Lin等[24]基于kV透视图提出了ROI模板匹配法用于无标记肿瘤跟踪,但基于MV图像的肿瘤跟踪研究较少。Arimura等[25]使用互相关算法将肿瘤模板与对应的EPID图像进行配准,获得了0.58到2.53 mm的跟踪精度,其中2 mm以下的成功率80%。Rottmann等[26]采用特征点检测和跟踪法对SBRT病例测量,获得了<2 mm的精度。这些研究没有考虑MLC遮挡导致数据缺失和靶区非刚性形变的问题,因此本研究方法更符合临床实际需要。本算法应对严重数据缺失(如仅剩余10%左右的图像数据)的匹配也具有鲁棒性,跟踪精度不亚于上述的方法(2 mm成功率达80%)。模体实验中各方向设置幅度为10 mm的治疗实际偏移量,以模拟最大可能肿瘤运动幅度。而算法测算出偏移量与实际偏移量偏差为2~3 mm,明显小于肿瘤运动幅度,认为本算法的跟踪精度可靠。
在图像相似性测度中,均方误差(MSE)、峰值信噪比(PNSR)等单模态的方法及NCC、NMI、结构相似性(SSIM)、豪斯多夫距离(HD)等多模态方法都被广泛应用。研究发现MV图像与KV图像的射线能量相差较大,其灰度值范围和亮度不同,因此在某种意义上属于多模态图像,MSE和PNSR等单模态方法不适用。而在EPID图像中,射野边缘存在MLC半影和伪影,本研究对其做了窗口内缩仍不能完全消除。这些半影和伪影对SSIM的测量值影响较大,导致错误的配准结果。NCC和NMI作为一种图像灰度的统计学分析方法,能够有效地消除图像亮度差异和灰度差异的影响[27],最终被用于本研究的初始配准相似度测度和配准结果评估。
模体实验配准的误差因素多方面。除了配准算法的偏差外,模体数据中靶区结构的轮廓勾画误差也是原因。另外,从模体结果中可以看到配准错误的图像对集中分布于20,40,60和90控制点附近。分析发现这些图像射野内出现了模体的脊椎,因其骨性结构形状较为简单且一致,其CT值较小球大,造成了配准的干扰。但临床数据中真实的脊柱结构相邻间有差异,且不单纯依靠靶区的规则形状去匹配,受其CT值的影响较小,不影响结果。此外,调强计划中会出现较多的小面积子野,以保证剂量分布需要。而MLC叶片半影伪影的存在导致可分析的图像区域更小,这也是配准失败的重要原因。
Wu等[16]在肺部靶区的运动研究中建议用刚性变换描述肿瘤的运动,但基于BEV投影图像配准算法只能分析垂直射野平面上的偏移,出现平行于射线方向的偏移会导致靶区出现微弱的大小变化,但对实际剂量造成影响不可忽视。另外,盆腔等区域由于器官蠕动变形、膀胱充盈变化、摆位差异等,导致靶区出现非刚性的形变。因此,研究中引入非刚性配准算法,一定程度上可以弥补这种情况。
与所有EPID配准方法的缺陷一样,本研究算法的成功率上限受制于EPID图像治疗野的大小和低对比度。另外本研究的实验数据是基于肺靶区病例,其骨性标志和肺的图像特性相对固定。对于其他部位(如盆腔等)因图像变化较大,增加更多的正确样本进行训练是必要的。该程序目前适用于回顾性验证,若用于临床实时监测,在程序结构优化、运行速度上还需要提高。
利益冲突 无
作者贡献声明 黄泰茗负责论文撰写、数据分析;钟嘉健、管棋负责临床数据收集与分析、参与调研;丘敏敏、罗宁负责数据收集与分析;邓永锦负责临床数据收集分析、论文修改
| [1] |
Vergalasova I, Cai J. A modern review of the uncertainties in volumetric imaging of respiratory-induced target motion in lung radiotherapy[J]. Med Phys, 2020, 47(10): e988-e1008. DOI:10.1002/mp.14312 |
| [2] |
Lo KM, Wu VW, Li Y, et al. Factors affecting target motion in stereotactic body radiotherapy of liver cancer using CyberKnife[J]. J Med Imaging Radiat Oncol, 2020, 64(3): 408-413. DOI:10.1111/1754-9485.13020 |
| [3] |
Sande E, Acosta Roa AM, Hellebust TP. Dose deviations induced by respiratory motion for radiotherapy of lung tumors: Impact of CT reconstruction, plan complexity, and fraction size[J]. J Appl Clin Med Phys, 2020, 21(4): 68-79. DOI:10.1002/acm2.12847 |
| [4] |
van Herk M. Errors and margins in radiotherapy[J]. Semin Radiat Oncol, 2004, 14(1): 52-64. DOI:10.1053/j.semradonc.2003.10.003 |
| [5] |
McKenzie AL. How should breathing motion be combined with other errors when drawing margins around clinical target volumes?[J]. Br J Radiol, 2000, 73(873): 973-977. DOI:10.1259/bjr.73.873.11064651 |
| [6] |
Bezjak A, Rumble RB, Rodrigues G, et al. Intensity-modulated radiotherapy in the treatment of lung cancer[J]. Clin Oncol (R Coll Radiol), 2012, 24(7): 508-520. DOI:10.1016/j.clon.2012.05.007 |
| [7] |
Gerszten PC, Ozhasoglu C, Burton SA, et al. CyberKnife frameless stereotactic radiosurgery for spinal lesions: clinical experience in 125 cases[J]. Neurosurgery, 2004, 55(1): 89-98. |
| [8] |
Harada T, Shirato H, Ogura S, et al. Real-time tumor-tracking radiation therapy for lung carcinoma by the aid of insertion of a gold marker using bronchofiberscopy[J]. Cancer, 2002, 95(8): 1720-1727. DOI:10.1002/cncr.10856 |
| [9] |
Patel R, Panfil J, Campana M, et al. Markerless motion tracking of lung tumors using dual-energy fluoroscopy[J]. Med Phys, 2015, 42(1): 254-262. DOI:10.1118/1.4903892 |
| [10] |
Bhagat N, Fidelman N, Durack JC, et al. Complications associated with the percutaneous insertion of fiducial markers in the thorax[J]. Cardiovasc Intervent Radiol, 2010, 33(6): 1186-1191. DOI:10.1007/s00270-010-9949-0 |
| [11] |
Nuyttens JJ, Prévost JB, Praag J, et al. Lung tumor tracking during stereotactic radiotherapy treatment with the CyberKnife: Marker placement and early results[J]. Acta Oncol, 2006, 45(7): 961-965. DOI:10.1080/02841860600902205 |
| [12] |
Straumann E, Yoon S, Naegeli B, et al. Hospital transfer for primary coronary angioplasty in high risk patients with acute myocardial infarction[J]. Heart, 1999, 82(4): 415-419. DOI:10.1136/hrt.82.4.415 |
| [13] |
Naumann P, Batista V, Farnia B, et al. Feasibility of optical surface-guidance for position verification and monitoring of stereotactic body radiotherapy in deep-inspiration breath-hold[J]. Front Oncol, 2020, 10: 573279. DOI:10.3389/fonc.2020.573279 |
| [14] |
Seppenwoolde Y, Berbeco RI, Nishioka S, et al. Accuracy of tumor motion compensation algorithm from a robotic respiratory tracking system: a simulation study[J]. Med Phys, 2007, 34(7): 2774-2784. DOI:10.1118/1.2739811 |
| [15] |
Moutrie V, Kairn T, Rosenfeld A, et al. Use of a megavoltage electronic portal imaging device to identify prosthetic materials[J]. Australas Phys Eng Sci Med, 2015, 38(1): 93-100. DOI:10.1007/s13246-015-0327-8 |
| [16] |
Wu J, Lei P, Shekhar R, et al. Do tumors in the lung deform during normal respiration? An image registration investigation[J]. Int J Radiat Oncol Biol Phys, 2009, 75(1): 268-275. DOI:10.1016/j.ijrobp.2009.03.008 |
| [17] |
Mesin L. Balanced multi-image demons for non-rigid registration of magnetic resonance images[J]. Magn Reson Imaging, 2020, 74: 128-138. DOI:10.1016/j.mri.2020.09.013 |
| [18] |
Deo RC. Machine learning in medicine[J]. Circulation, 2015, 132(20): 1920-1930. DOI:10.1161/CIRCULATIONAHA.115.001593 |
| [19] |
Balakrishnan G, Zhao A, Sabuncu MR, et al. VoxelMorph: A learning framework for deformable medical image registration[J]. IEEE Trans Med Imaging, 2019. DOI:10.1109/TMI.2019.2897538 |
| [20] |
Fanizzi A, Basile T, Losurdo L, et al. A machine learning approach on multiscale texture analysis for breast microcalcification diagnosis[J]. BMC Bioinformatics, 2020, 21(Suppl 2): 91. DOI:10.1186/s12859-020-3358-4 |
| [21] |
Belmont B, Kessler R, Theyyunni N, et al. Continuous inferior vena cava diameter tracking through an iterative Kanade-Lucas-Tomasi-based algorithm[J]. Ultrasound Med Biol, 2018, 44(12): 2793-2801. DOI:10.1016/j.ultrasmedbio.2018.07.022 |
| [22] |
Lee H, Cho A, Lee S, et al. Vision-based measurement of heart rate from ballistocardiographic head movements using unsupervised clustering[J]. Sensors (Basel), 2019, 19(15). DOI:10.3390/s19153263 |
| [23] |
Cui Y, Dy JG, Alexander B, et al. Fluoroscopic gating without implanted fiducial markers for lung cancer radiotherapy based on support vector machines[J]. Phys Med Biol, 2008, 53(16): N315-327. DOI:10.1088/0031-9155/53/16/N01 |
| [24] |
Lin T, Cerviño LI, Tang X, et al. Fluoroscopic tumor tracking for image-guided lung cancer radiotherapy[J]. Phys Med Biol, 2009, 54(4): 981-992. DOI:10.1088/0031-9155/54/4/011 |
| [25] |
Arimura H, Egashira Y, Shioyama Y, et al. Computerized method for estimation of the location of a lung tumor on EPID cine images without implanted markers in stereotactic body radiotherapy[J]. Phys Med Biol, 2009, 54(3): 665-677. DOI:10.1088/0031-9155/54/3/013 |
| [26] |
Rottmann J, Aristophanous M, Chen A, et al. A multi-region algorithm for markerless beam's-eye view lung tumor tracking[J]. Phys Med Biol, 2010, 55(18): 5585-5598. DOI:10.1088/0031-9155/55/18/021 |
| [27] |
Yang T, Tang Q, Li L, et al. Nonrigid registration of medical image based on adaptive local structure tensor and normalized mutual information[J]. J Appl Clin Med Phys, 2019, 20(6): 99-110. DOI:10.1002/acm2.12612 |
 2022, Vol. 42
2022, Vol. 42


