由多个电离室或半导体探测单元按一定规则排列组成的探测器矩阵(以下简称矩阵)可以方便实现辐射剂量分布测量,随着调强放射治疗技术的逐渐开展,矩阵已广泛用于调强辐射野绝对剂量和剂量分布的测量[1-2],测量参数包括辐射野尺寸、平坦度和对称性等,该设备已经成为放疗质控的重要工具[3-4]。矩阵根据各个独立探测单元的测量结果获得被测区域剂量分布的信息,而各个探测单元的响应可能存在差异。因此,为保证剂量分布测量结果可靠,需要确定各个探测单元之间的相对响应关系(以下简称相对响应),并依此对矩阵测量结果进行修正,相对响应同时也是放疗质量控制的基本要素之一。
相对响应指各个探测单元的响应或校准因子相对于参考探测单元响应或校准因子的比值。理论上,通过测量一个剂量分布已知的辐射场可以获得矩阵相对响应的结果,但受限于测量或计算方法,辐射场剂量分布结果与实际情况存在偏差,同时受辐射装置自身稳定性的影响无法形成剂量分布完全相同的辐射场,导致相对响应结果存在问题。另外,通过比较矩阵各个探测单元对于相同辐射的测量结果,也可以获得相对响应的结果,最直接的方法就是采用稳定的辐射束,使组成矩阵的每个探测单元依次接受相同辐射,从而获得相对响应的评价结果[2],如果探测单元数量多,此方法非常耗时,由于检测时间过长,探测单元响应还会随时间发生变化从而影响相对响应的结果,因此可操作性较差。本研究提出了一种基于矩阵平移、结合递归算法的矩阵相对响应检测方法。
材料与方法1.实验设备与软件
(1) 探测器矩阵:测量区域内等间距均匀分布了1 020个电离室型探测单元,排列方式为32 × 32,每个电离室外径为4.5 mm高5 mm,灵敏体积0.08 cm3,相邻电离室探测单元中心间距7.62 mm,探测区域有效测量面积24 cm × 24 cm。
(2) 辐射装置:瑞典Elekta公司生产的Synergy医用直线加速器。
(3) 计算软件:美国Origin Lab公司开发的Origin科学绘图、数据分析软件。
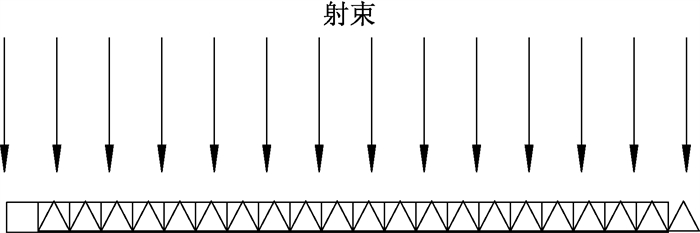
2.检测原理:简化起见,以一维矩阵为例阐述检测原理。先将一维矩阵置于1个稳定的辐射场中采集第一组测量数据,再将一维矩阵沿探测单元排列方向平移一个探测单元的间距,在相同的辐射条件下采集第二组测量数据,矩阵与辐射野相对位置的变化见图 1(向右平移)。
|
注:图中方格表示矩阵探测单元采集第1组数据的位置,三角表示平移1个探测单元间距后的位置。 图 1 一维探测单元矩阵位置变化示意图 Figure 1 Sketch map of position change of one-dimensional detection unit matrix |
假设组成一维矩阵的探测单元从左至右为d1、d2、……、di(i=1、2、…、n,n为探测单元数量),通过向右平移,d1占据了d2原来的位置,d2占据了d3原来的位置,……,di-1占据了di原来的位置,对于一个辐射野而言,位置相同意味着辐射剂量相同,因而可以获得探测单元d1和d2、探测单元d2和d3、探测单元d3和d4,直至探测单元di-1和di的相对响应。同时,由探测单元d1和d2的相对响应和探测单元d2和d3的相对响应,可以获得探测单元d1和d3的相对响应;利用探测单元d1和d3的相对响应和探测单元d3和d4的相对响应,可以获得探测单元d1和d4的相对响应,以此类推,经过n-2次运算,就可以获得探测单元d1与一维矩阵中其它各个探测单元的相对响应。
3.检测方法
(1) 检测步骤:实际检测过程中,由于测量数据分次获得,每次照射条件可能存在差异,探测单元的响应在不同检测步骤中也可能会发生微小变化,这两种变化造成的影响会随递归算法传播至整个矩阵并随着探测单元的数量线性增加,导致相对响应结果的偏差逐渐增大。为修正这些影响,在检测步骤中设置一个获取参考数据的步骤,称为参考步骤,根据其他步骤与参考步骤中矩阵的相对位置关系,将其他步骤的数据修正到参考步骤的条件下,就可消除辐射条件变化和探测单元相对响应变化的影响。下面以最为常见的二维矩阵为例,具体步骤如下:
① 设置辐射野尺寸,保证矩阵测量区域外的部分不受到辐射。
② 测量并获取第1组数据(步骤A)。
③ 将矩阵沿水平方向平移一个探测单元的间距。
④ 测量并获取第2组数据(步骤B)。
⑤ 将矩阵恢复为获取数据B的位置后,沿竖直方向平移一个探测器单元的间距。
⑥ 测量并获取第3组数据(步骤C)。
⑦ 将矩阵恢复为步骤A的位置后,以矩阵探测区域几何中心为圆心将矩阵旋转180°。
⑧ 测量并获取第4组数据(步骤D)。
上述步骤中获取第4组数据的步骤D为参考步骤。
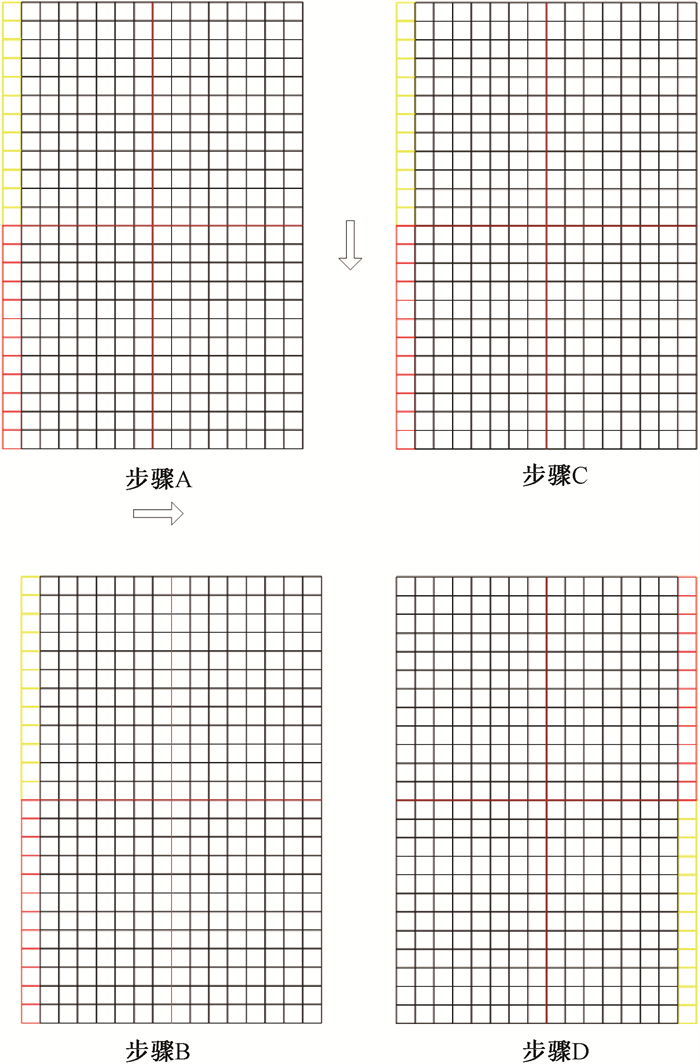
以n×m的矩阵为例,其中n为矩阵探测单元的行数,m为矩阵探测单元的列数,i和j为标记探测单元位置的角标,i=1、2、3、……、n,j=1、2、3、……、m,后续计算和分析过程中该角标不随矩阵方位变化。步骤A、B、C和D的矩阵相对位置见图 2。原则上矩阵旋转方向和平移方向可以任意选择,实际测试中采用了图 2中箭头所示的平移方向,由于旋转角度为180°,顺时针和逆时针结果一样,因此旋转方向无需特别说明。
|
注:图中箭头表示矩阵平移的方向;红、黄、黑色表示矩阵位置变化时,矩阵里第1列探测单元的位置变化 图 2 矩阵获取数据时的相对位置示意图 Figure 2 Sketch map of relative position during matrix obtaining data |
(2) 数据处理:如果检测过程中辐射条件没有发生变化,由步骤A和B中矩阵的相对位置关系可以得到式(1)。
| $ {F_{i, j + 1}} = {N_{i, j}} \times {B_{i, j}} = {N_{i, j + 1}} \times {A_{i, j + 1}} $ | (1) |
式中,Fi, j +1为探测单元(i, j+1)和探测单元(i, j)分别在步骤A和步骤B中对应的同一位置的剂量,Ni, j和Ni, j +1分别为探测单元(i, j)在步骤B中探测单元(i, j+1)步骤A中的校准因子,Bi, j和Ai, j +1分别为探测单元(i, j)在步骤B中探测单元(i, j+1)步骤A中的测量结果。
根据式(1),矩阵每一行中两两相邻的探测单元的相对响应如下:
| $ {R_{i, j + 1/i, j}} = \frac{{{N_{i, j + 1}}}}{{{N_{i, j}}}} = \frac{{{B_{i, j}}}}{{{A_{i, j + 1}}}} $ | (2) |
式中,Ri, j +1/ i, j为探测单元(i, j+1)相对于探测单元(i, j)的相对响应。
由式(2)可以推导出每行探测单元相对该行最左侧探测单元相对响应的计算公式:
| $ \begin{array}{c} {R_{i, j/i, 1}} = \frac{{{B_{i, 1}}}}{{{A_{i, 2}}}} \times \frac{{{B_{i, 2}}}}{{{A_{i, 3}}}} \times \cdots \cdots \times \\ \frac{{{B_{i, j - 1}}}}{{{A_{i, j}}}} = \frac{{\prod_{j = 1}^{j - 1} {{B_{i, j}}} }}{{\prod_{j = 2}^j {{A_{i, j}}} }}(j = 2{\rm{、、}}3{\rm{、、}} \cdots \cdots 、、m) \end{array} $ | (3) |
同理,由步骤A和步骤C可以获得每列探测单元相对该列第1个探测单元相对响应的计算公式:
| $ \begin{array}{c} {R_{i, j/1, j}} = \frac{{{C_{1, j}}}}{{{A_{2, j}}}} \times \frac{{{C_{2, j}}}}{{{A_{3, j}}}} \times \cdots \cdots \times \\ \frac{{{C_{n - 1, j}}}}{{{A_{n, j}}}} = \frac{{\prod_{i = 1}^{i - 1} {{C_{i, j}}} }}{{\prod_{i = 2}^i {{A_{i, j}}} }}(i = 2{\rm{、、}}3、、\cdots \cdots 、、n) \end{array} $ | (4) |
式中,Ci, j为探测单元(i, j)在步骤C中的测量读数。
如前所述,每个步骤的辐射条件和探测单元的响应都可能发生变化,因此需要获得对于这两个变化的修正,式(3)、(4)才能成立。为此将矩阵以探测平面中心为圆心旋转180°(步骤D),探测单元(i, j)在步骤A中的位置被探测单元(n-i+1, m-j+1)占据,矩阵整个探测区域对应的辐射区域位置没有变化,假设辐射野剂量分布和相对响应没有变化,步骤A和步骤D存在以下关系:
| $ \begin{array}{c} {F_{i, j}} = {A_{i, j}} \times {N_{i, j}} \times {f_{i, {j_{AD}}}} = \\ {D_{n - i + 1, m - j + 1}} \times {N_{n - i + 1, m - j + 1}} \end{array} $ | (5) |
式中,fi, jAD为将步骤A各个探测单元的数据修正到步骤D条件的修正因子,该修正因子将辐射条件的变化和探测单元响应的变化平均分配给每个探测单元,因此,fi, jAD可以写为fAD;Dn - i +1, m - j +1和Nn - i +1, m - j +1分别为探测单元(n-i+1, m-j+1)在步骤D的测量读数和校准因子。另外,式(5)中的角标i, j分别为步骤A中各个探测单元行和列的标记。由于各个探测单元的校准因子及其对应的辐射剂量未知,因此由式(5)依然无法计算fAD,但对于整个探测区域则有以下关系:
| $ \prod\limits_{i = 1}^n {\prod\limits_{j = 1}^m {{A_{i, j}}} } \cdot {N_{i, j}} \cdots {f_{{\rm{AD}}}} = \prod\limits_{i = 1}^n {\prod\limits_{j = 1}^m {{D_{i, j}}} } \cdot {N_{i, j}} $ | (6) |
由式(6)可得,
| $ {\left( {{f_{{\rm{AD}}}}} \right)^{n \cdot m}} = \frac{{\prod_{i = 1}^n {\prod_{j = 1}^m {{D_{i, j}}} } }}{{\prod_{i = 1}^n {\prod_{j = 1}^m {{A_{i, j}}} } }} $ | (7) |
对式(7)两边取对数,得到将步骤A的数据修正到步骤D条件的修正因子fAD的计算公式:
| $ {f_{{\rm{AD}}}} = {{\rm{e}}^{\frac{{\sum_{i = 1}^n {\sum_{j = 1}^m {\ln } } {D_{i, j}} - \sum_{i = 1}^n {\sum_{j = 1}^m {\ln } } {A_{i, j}}}}{{n \cdot m}}}} $ | (8) |
由矩阵在步骤A和步骤B的相对位置,根据式(3)位于矩阵两端的两列探测单元的相对响应乘积为:
| $ \begin{array}{c} \prod\limits_{i = 1}^n {{R_{i, m/i, 1}}} = \prod\limits_{i = 1}^n {\left( {\frac{{{B_{i, 1}}}}{{{A_{i, 2}}}} \times \frac{{{B_{i, 2}}}}{{{A_{i, 3}}}} \times \cdots \cdots \times \frac{{{B_{i, m - 1}}}}{{{A_{i, m}}}} \times {{\left( {{f_{{\rm{BD}}}}} \right)}^{m - 1}}} \right)} = \\ f_{{\rm{BD}}}^{n \times (m - 1)} \cdot \prod\limits_{i = 1}^n {\left( {\frac{{\prod_{j = 1}^{m - 1} {{B_{i, j}}} }}{{\prod_{j = 2}^m {{A_{i, j}}} }}} \right)} \end{array} $ | (9) |
式中,fBD为将步骤B各个探测单元的数据修正到步骤D条件的修正因子。式(8)及文中后续的分析计算中,步骤A的数据已经相对于步骤D进行了修正,即Ai, j = fAD · Ai, j。
由矩阵在步骤A和步骤D的相对位置,根据公式(3)可以获得以下一系列关系式。
| $ \begin{array}{*{20}{c}} {{N_{1, 1}} \times {A_{1, 1}} = {N_{n, m}} \times {D_{n, m}} = {R_{n, m/n, 1}} \times {N_{n, 1}} \times {D_{n, m}}}\\ \begin{array}{c} {N_{2, 1}} \times {A_{2, 1}} = {N_{n - 1, m}} \times {D_{n - 1, m}} = {R_{n - 1, m/n - 1, 1}} \times {N_{n - 1, 1}} \times {D_{n - 1, m}}\\ \cdots \cdots \end{array}\\ {{N_{n, 1}} \times {A_{n, 1}} = {N_{1, m}} \times {D_{1, m}} = {R_{1, m/1, 1}} \times {N_{1, 1}} \times {D_{1, m}}} \end{array} $ | (10) |
由式(10),可以推导出,
| $ \prod\limits_{i = 1}^n {{N_{i, 1}}} \times {A_{i, 1}} = \prod\limits_{i = 1}^n {{R_{i, m/i, 1}}} \times {N_{i, 1}} \times {D_{i, m}} $ | (11) |
则,
| $ \prod\limits_{i = 1}^n {{R_{i, m/i, 1}}} = \frac{{\prod_{i = 1}^n {{A_{i, 1}}} }}{{\prod_{i = 1}^n {{D_{i, m}}} }} $ | (12) |
由式(8)和(12)可得,
| $ {\left( {{f_{{\rm{BD}}}}} \right)^{n \times (m - 1)}} = \prod\limits_{i = 1}^n {\left( {{A_{i, 1}}/{D_{i, m}}} \right)} /\prod\limits_{i = 1}^n {\left( {\prod\limits_{j = 1}^{m - 1} {{B_{i, j}}} /\prod\limits_{j = 2}^m {{A_{i, j}}} } \right)} $ | (13) |
对式(13)两边取对数,可以获得步骤B的数据相对于步骤D条件的修正因子的计算公式。
| $ {f_{{\rm{BD}}}} = {{\rm{e}}^{\frac{{\sum_{i = 1}^n {\sum_{j = 1}^m {\ln } } {A_{i, j}} - \sum_{i = 1}^n {\ln } {D_{i, m}} - \sum_{i = 1}^n {\sum_{j = 1}^{m - 1} {\ln } } {B_{i, j}}}}{{n \times m}}}} $ | (14) |
同理,步骤C数据相对于步骤D条件的修正因子的计算公式如下。
| $ {\left( {{f_{{\rm{CD}}}}} \right)^{n \times (m - 1)}} = \prod\limits_{j = 1}^m {\left( {{A_{1, j}}/{D_{1, j}}} \right)} /\prod\limits_{j = 1}^m {\left( {\prod\limits_{i = 1}^{n - 1} {{C_{i, j}}} /\prod\limits_{i = 2}^n {{A_{i, j}}} } \right)} $ | (15) |
| $ {f_{{\rm{CD}}}} = {{\rm{e}}^{\frac{{\sum_{i = 1}^n {\sum_{j = 1}^m {\ln } } {A_{i, j}} - \sum_{j = 1}^m {\ln } {D_{1, j}} - \sum_{j = 1}^m {\sum_{i = 1}^{n - 1} {\ln } } {C_{i, j}}}}{{n \times m}}}} $ | (16) |
步骤A、B和C的测量数据分别乘以各自的修正因子fAD、fBD和fCD后,不同步骤的测量结果均修正到步骤D的条件下,从而消除了辐射条件和探测单元响应变化的影响。
数据修正后,根据式(3)可以获得每一行探测单元相对该行第1个探测单元(i, 1)的相对响应,再根据式(4)可以获得矩阵每一列探测单元相对于该列第1个探测单元(1, j)的相对响应,由于每行探测单元的相对响应已知,因此只要获得1列探测单元的相对响应即可获得整个矩阵各个探测单元相对于探测单元(1, 1)的相对响应。
结果1.验证实验及结果
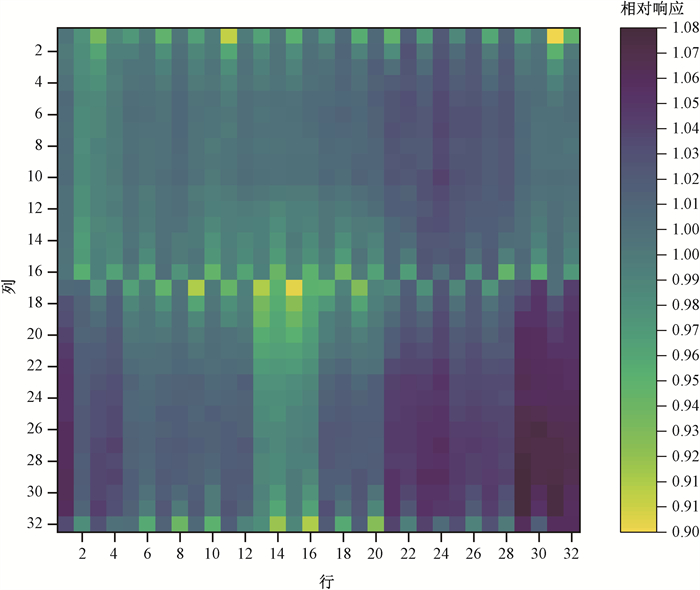
(1) 验证实验:采用上述方法对1个矩阵进行了验证测试,该矩阵具体信息如前所述。检测时,矩阵测量平面距加速器焦点100 cm,辐射野尺寸26 cm × 26 cm,矩阵探测区域中心与光野十字线中心重合,加速器输出剂量率为100 MU/min。经过前述步骤和公式,fAD=1.002 99,fBD=1.004 69,fCD=1.002 59。将编号为(1, 1)探测单元设为参考探测单元,该探测单元的响应设置为1,相对响应检测结果见图 3。
|
图 3 矩阵相对响应验证检测结果 Figure 3 Test results of relative response verification of matrix |
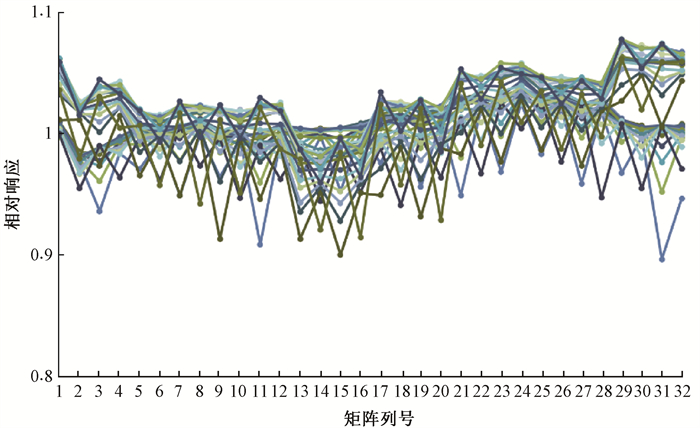
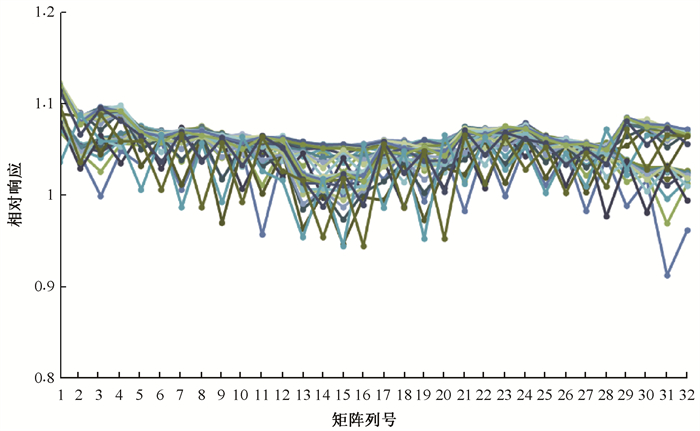
(2) 结果确认:理论上,通过自动扫描水模体系统(即三维水箱)和矩阵对同一辐射野的测量结果直接比较可以直观地获得矩阵各个测量单元相对响应检测结果的评价,由于每次测量时辐射野都存在变化的可能,三维水箱和矩阵的测量结果可能存在偏差,因此直接比较的结果无法准确评价矩阵相对响应的检测结果。如前所述,如果不修正检测过程中辐射条件和探测单元响应的变化,辐射条件和探测单元响应变化的影响会随探测单元的数量线性增加,导致相对响应的整体结果呈上升或下降趋势,因此根据相对响应的变化趋势可以判断修正方法的合理性。由于用于测试的矩阵和提供辐射的加速器稳定性较好,从相对响应结果看,修正和未修正的数据差别并不明显,但修正和未修正的每行探测单元相对响应变化趋势仍然可以看出(图 4,5),未修正的相对响应结果整体呈现了单调下降趋势,而修正后相对响应结果整体呈现随机分布,说明本方法可以准确给出矩阵相对响应的结果。
|
注:图中每条曲线代表矩阵每行探测单元的相对响应 图 4 经修正后每行探测单元相对响应变化趋势 Figure 4 Varing trend in relative response of detection unit per line after correction |
|
注:图中每条曲线代表矩阵每行探测单元的相对响应 图 5 未修正的每行探测单元相对响应变化趋势 Figure 5 Varing trend in relative response of detection unit per line before correction |
2.不确定度分析:根据相对响应的检测方法和计算过程,相对响应结果的不确定度来源主要包括矩阵旋转的定位偏差、矩阵平移的定位偏差、矩阵探测区域平面的水平、检测过程中辐射分布变化和探测器响应变化。
加速器光野定位十字线和定位指示激光线的宽度、矩阵旋转角度尺以及平移标尺分辨率的影响,矩阵旋转、平移以及调整水平时位置可能出现偏差,该偏差导致矩阵探测区域对应的辐射野存在偏差,由于检测采用的辐射野的均整区略大于矩阵探测区域的面积,在不同步骤时均能完全覆盖矩阵探测区域,考虑辐射野均整区剂量分布的情况,矩阵位置偏差对相对响应结果不确定度的贡献为0.3%。根据检测用加速器设备的测量结果,加速器输出的重复性为0.1%,辐射野平坦度重复性为0.03%,结合4个获取数据的步骤,辐射野剂量分布变化对相对响应结果不确定度的贡献为0.2%。探测单元响应变化采用输出稳定60Co辐照装置评价,各探测单元测量重复性在0.05%至0.07%之间变化,探测单元响应变化对相对响应结果不确定度的贡献为0.14%。根据不确定度合成定理[5],矩阵相对响应结果的合成标准不确定度为0.4%。
讨论相对响应是矩阵最关键和最基础的参数之一,本方法简便易行,可用于确定一维和二维矩阵的相对响应。通过平移矩阵使得矩阵两两相邻的探测单元测量相同的辐射,建立了相邻两个探测单元的相对响应关系,再通过递归算法确定了所有探测单元的相对响应,同时本方法通过旋转矩阵,根据各个探测单元在不同步骤的相对位置关系,消除了检测过程中辐射条件变化和探测单元响应变化对检测结果的影响,实际验证实验结果表明本方法可以准确获得相对响应的结果,相对响应检测结果的扩展不确定度为0.8%(k=2)。此外,通过改变矩阵在辐射野中的位置实现相邻两个探测单元接受相同辐射,辐射野只需覆盖矩阵的探测区域而无需知道剂量分布情况,避免了辐射野剂量分布结果的不确定度对相对响应结果的影响,但为降低对矩阵位置变化准确度的要求,则应尽可能采用剂量分布均匀的辐射野进行检测,同时为保护与矩阵探测区域相邻的测量电路,需要避免测量电路受到辐射。组成矩阵的探测单元主要分为电离室和半导体两类,无论电离室还是半导体探测器都存在能量响应、角响应、剂量率响应、线性、稳定性、重复性等特性,而且各个探测单元的变化趋势不尽相同,因此评价上述参数时也需考虑相对响应的问题。
目前国际上还有两种基于上述原理的相对响应检测方法,一种是Simon等[6]发明的方法,包含90°和180°两次旋转和1次平移的步骤,适用于多种排列方式的矩阵,英国国家物理实验室(NPL)采用该方法校准矩阵相对响应;另一种是Donetti等[7]的方法包含1次90°旋转和1次平移的步骤,但仅适用于正方形矩阵,该方法被德国IBA公司用于本公司矩阵产品的调试。本文叙述的方法包括1次180°旋转和2次平移的步骤,其中2次平移的方向互相垂直,与Simon等[6]的方法相比,本方法只有1次180°的旋转,降低了旋转角度偏差带来探测单元位置偏差的几率,同时计算过程简单明晰,与Donetti等[7]的方法相比,尽管本方法多了一步平移,但适用于多种排列方式的矩阵,具有更加广泛的适用性。本方法的思路除适用于放疗矩阵相对响应关系确定为放疗质控提供基础数据外,也为光学、声学等其它领域的探测器矩阵相对响应关系确定提供了一种解决方案。
利益冲突 无
志谢 感谢北京大学肿瘤医院的吴昊老师、岳海振老师和张艺宝老师对本项工作的指导与协助
作者贡献声明 第1作者张辉(指导老师)负责方法创建、归纳及实验验证、论文撰写;第2作者张辉(研究生)负责文献收集、整理及实验;王平全参与文献查阅、论文撰写、数据整理;杨竣凯负责指导文献查阅和论文撰写;王坤指导论文修改
| [1] |
Poppe B, Blechschmidt A, Djouguela A, et al. Two-dimensional ionization chamber arrays for IMRT plan verification[J]. Med Phys, 2006, 33(4): 1005-1015. DOI:10.1118/1.2179167 |
| [2] |
Herzen J, Todorovic M, Cremers F, et al. Dosimetric evaluation of a 2D pixel ionization chamber for implementation in clinical routine[J]. Phys Med Biol, 2007, 52(4): 1197-1208. DOI:10.1088/0031-9155/52/4/023 |
| [3] |
Wang S, Li Z, Chao KS, et al. Calibration of a detector array through beam profile reconstruction with error-locking[J]. J Appl Clin Med Phys, 2014, 15(6): 4591. DOI:10.1120/jacmp.v15i6.4591 |
| [4] |
翟贺争, 程金生, 丁艳秋, 等. 二维电离室矩阵探测器的光子剂量学性能测试[J]. 中华放射医学与防护杂志, 2015, 35(2): 144-148. Zhai HZ, Cheng JS, Ding YQ, et al. Test of dosimetric characteristics 2-D matrix detector in photon beams[J]. Chin J Radiol Med Prot, 2015, 35(2): 144-148. DOI:10.3760/cma.j.issn.0254-5098.2015.02.017 |
| [5] |
倪育才. 实用测量不确定度评定[M]. 第6版. 北京: 中国质量标准出版传媒有限公司, 2020. Ni YC. Evaluation of practical measurement uncertainty[M]. 6th ed. Beijing: China Quality Standards Publishing Media Co., Ltd, 2020. |
| [6] |
Simon WE, Shi J, Craig A, et al. Wide field calibration of a multi-sensor array: USA, Patent 6125335A[P]. 2000-09-26.
|
| [7] |
Donetti M, Garelli E, Marchetto F, et al. A method for the inter-calibration of a matrix of sensors[J]. Phys Med Biol, 2006, 51(3): 485-495. DOI:10.1088/0031-9155/51/3/002 |
 2022, Vol. 42
2022, Vol. 42


