2. 广州医科大学附属肿瘤医院放疗中心 510095
2. Radiotherapy Center, Affiliated Tumor Hospital of Guangzhou Medical University, Guangzhou 510095, China
磁共振加速器(MR-Linac)开辟了图像引导精确放疗的新格局,相比于常规放疗,磁共振图像引导放疗(MRgRT)具有更优的软组织成像分辨力、成像过程无辐射、无需繁琐的摆位和体位固定、可实现肿瘤位置与运动的实时监控以及在线自适应计划等优势[1-4]。目前国内有多家放疗中心已经安装了瑞曲医科达公司的Unity MR-Linac系统,该系统结合了医科达7 MV无均整器设计的加速器和荷兰飞利浦1.5 T Ingenia磁共振扫描仪,磁场方向始终与射束方向垂直[4-5]。
光子与物质发生相互作用会产生大量次级电子,Unity系统1.5 T垂直磁场的存在会影响次级电子的运动轨迹,引起剂量分布的改变,在不同密度介质交界面附近出现电子回转效应(electron return effect, ERE)[6-7],而在体外空气中则会出现电子流效应(electron stream effect, ESE)[7]。ERE和ESE都是MR-Linac系统所特有的现象,对于ERE的研究已有较多文献报道[8-10],而针对ESE效应的研究还很少,国内目前尚无报道。相比于ERE,ESE往往更难被注意到,因为ESE主要出现在射野外空气中,而在常规计划设计时,一般只考虑人体轮廓线以内的区域,无法显示出轮廓以外空气中的剂量,这就导致对体外ESE的忽视。但实际上,体外的电子流会在磁场作用下向磁场两极运动,飘移到射野外未知区域,可能对正常组织造成额外损伤,因此研究MR-Linac系统中的ESE是很有必要的[11-12]。本文主要针对Unity MR-Linac系统上的射野外ESE现象,研究了在均匀模体和临床病例调强治疗计划中的ESE对皮肤剂量的影响,为磁共振引导放疗技术的临床应用提供参考。
材料与方法 1、Monaco系统与GPUMCD计算引擎本研究采用了Unity MR-Linac系统专门配备的治疗计划系统(treatment planning system, TPS)Monaco(v5.40.1),其与常规Monaco的主要区别是采用了GPUMCD剂量计算引擎,而常规Monaco则采用了XVMC[13-14]。GPUMCD与XVMC都采用了蒙特卡罗剂量算法,二者在虚拟源建模方面也是一致的,采用了三源模型(初级光子源、次级光子源和污染电子源),所不同的是GPUMCD引擎可以准确计算出磁场下电子的剂量分布,同时也利用了GPU硬件对计算进行加速[14]。对于磁场下的电子输运,GPUMCD采用了4阶Runge-Kutta方法来求解电子耦合输运的微分方程,只考虑洛伦兹力的影响,并且认为磁场强度在空间内是均匀分布的[15]。
2、研究规则模体外的ESE首先基于规则几何的均匀水模体,分别研究单个照射野入射情况下,模体入射端和出射端的ESE。为了在TPS中更明显地观察到ESE的作用,本研究在Monaco系统中构建了两个规则几何的水模体,分别设计在束流出射端或入射端,模体表面倾斜,以观察空气中电子流的范围。模体在矢状面的剖面为梯形,短边8 cm,长边15 cm,高30 cm。水模体外围空间填充为空气,整个计算区域的外轮廓尺寸为50 cm × 50 cm × 50 cm。主要关注区域为模体外出射端和入射端的斜边附近,空气中的电子流剂量分布。照射野大小设置为5 cm × 5 cm,处方剂量为1 000 cGy,等中心设置在模体与空气交界面斜边的中心。为了与常规情况进行对比,还计算了在同样模体和射野布局情况下,没有磁场存在时计算区域内的剂量分布。所有计算采用的剂量网格大小为1 mm,所设置的计算统计误差为每个控制点<1%。
3、研究喉癌和乳腺癌临床病例中的ESE为了研究磁场下ESE对实际临床病例的射野外剂量影响,本研究回顾性地选取1例喉癌病例和1例乳腺癌病例,此前均在常规加速器上接受过调强放射治疗(IMRT),将其计划CT数据导入到MR-Linac专用的TPS Monaco系统中,沿用原计划的处方(喉癌病例为56 Gy/20次,乳腺癌病例为50 Gy/20次)和布野方式(喉癌病例9个射野的角度分别为0°、40°、80°、110°、160°、200°、250°、280°、320°;乳腺癌病例7个射野的角度分别为25°、50°、220°、250°、280°、330°、350°)。计划设计中机器模型选择考虑了磁场的Unity模型,设置剂量计算模式为“Dose to medium”,计算网格大小设为1 mm, 统计误差控制在每个控制点<1%。为了便于观察和对比磁场作用带来的射野外剂量分布改变,上述两个病例还分别设计了一个无磁场的计划,保持该计划的所有机器参数和计划参数与原始有磁场计划完全一致,仅在无磁场情况下重新进行了剂量计算,排除机器和计划参数等带来的影响。为了评估皮肤的受照剂量,将体表外轮廓内缩5 mm来代表皮肤区域。对于蒙特卡罗计算结果,为避免在使用点剂量评估时存在较大的统计误差,使用皮肤区域1 cm3体积所接受的最小剂量D1 cm3来评估其受到的最大剂量。
4、研究外加防护膜对磁场下ESE的防护考虑到ESE主要来源于散射到空气中的次级电子,其能量一般相对较低,比较容易被阻挡。本研究针对上述乳腺癌病例的调强计划,在下颌位置虚拟添加1 cm厚防护膜,探究其对ESE的衰减作用。其中防护膜材料在Monaco系统中定义为水。保持计划参数和条件不变,重新计算磁场下添加有防护膜后的剂量分布。将添加防护膜后的下颌剂量分布与原始计划未加防护膜的剂量进行对比,评估防护膜对磁场下ESE的衰减效果。
结果 1、规则几何模体外空气中的ESE结果如图 1所示,对于存在磁场的情况,水模体与空气交界面斜边位置出现了明显的电子回转效应ERE,而在沿磁场(或者背离磁场)的射野外空气中则观察到电子流效应ESE。这两种现象在无磁场情况下均未观察到。当存在磁场作用时,从模体中产生的散射电子进入到空气中,受磁场作用汇聚形成电子流,向沿磁场或背离磁场方向漂移。电子流在空气中不断漂移并逐渐衰减,对比出射端和入射端射野外的ESE结果可以发现,出射端的射野外ESE明显高于入射端。等中心平面入射端射野外2 cm处空气中ESE剂量为30.4 cGy,而出射端射野外2 cm则为85.6 cGy,主要是因为在出射端的次级电子数目较多,磁场下汇聚的电子流更强。而入射端空气中电子流主要来自背散射,次级电子数目较少,因此ESE相对较弱。
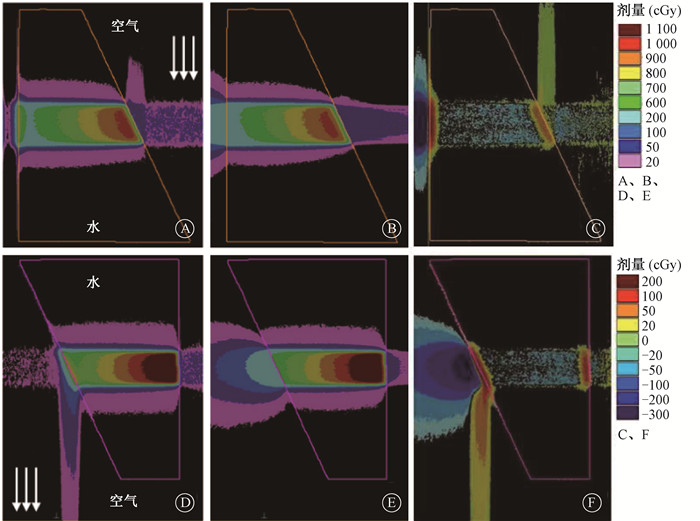
|
图 1 不同磁场情况下均匀照射野在规则几何模体上的射野外空气中ESE剂量分布 A.磁场存在下模体入射端的ESE剂量分布;B.无磁场下模体入射端的的ESE剂量分布;C.模体入射端有、无磁场的剂量差异;D.磁场存在下模体出射端的的ESE剂量分布;E.无磁场下模体出射端的的ESE剂量分布;F.模体出射端有、无磁场的剂量差异 Figure 1 Out-of-field in-air ESE-induced dose distribution in a square field of the regular geometry water phantom irradiated by different magnetic fields A. ESE-induced dose distribution on the entry side of phantom in the presence of a magnetic field; B. ESE-induced dose distribution on the entry side of phantom in the absence of a magnetic field; C. Dose difference on the entry side of phantom between the cases with and without a magnetic field; D. ESE-induced dose distribution on the exit side of phantom in the presence of a magnetic field; E. ESE-induced dose distribution on the exit side of phantom in the absence of a magnetic field; F. Dose difference on the exit side of phantom between the cases with and without a magnetic field |
2、喉癌和乳腺癌病例中的ESE结果
在临床病例的调强治疗计划中,一般需要用到多个照射野的情况,因此实际情况下ESE的来源既有入射端的背散射电子,也有出射端的散射电子。针对喉癌病例,差别较大的区域主要表现在射野内颈部的皮肤区域,局部差异可达5%以上, 但这部分的差异主要由电子回转效应ERE引起。对比射野外的剂量分布,有磁场的计划中射野外体表皮肤剂量分布稍微高于无磁场的结果,但总体差别非常小,大部分区域的皮肤剂量差异都在处方剂量(5 600 cGy)的2%以内,说明ESE对喉癌病例射野外皮肤剂量影响很小,见图 2。
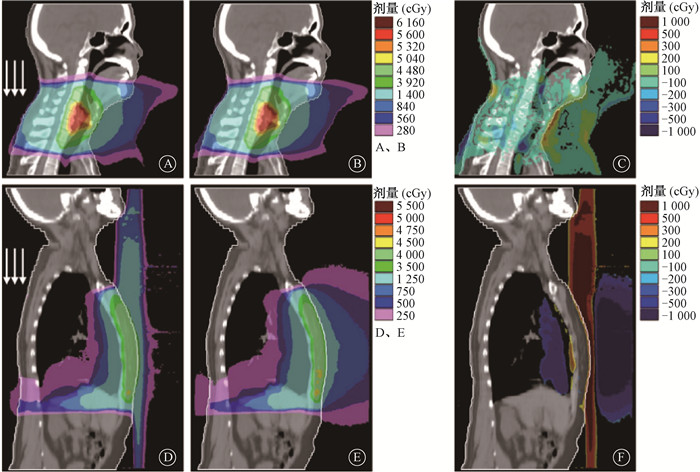
|
图 2 不同磁场情况下喉癌和乳腺癌病例的射野外空气中ESE剂量分布 A.磁场存在下喉癌病例的ESE剂量分布;B.无磁场下喉癌病例的ESE剂量分布;C.喉癌病例有、无磁场的剂量差异;D.磁场存在下乳腺癌病例的ESE剂量分布;E.无磁场下乳腺癌病例的ESE剂量分布;F.乳腺癌病例有、无磁场的剂量差异 Figure 2 Out-of-field in-air ESE-induced dose distribution for the laryngeal cancer case and the breast cancer case in different magnetic fields A. ESE-induced dose distribution for the laryngeal cancer case in the presence of a magnetic field; B. ESE-induced dose distribution for the laryngeal cancer case in the absence of a magnetic field; C. Dose difference for the laryngeal cancer case between the cases with and without a magnetic field; D. ESE-induced dose distribution for the breast cancer case in the presence of a magnetic field; E. ESE-induced dose distribution for the breast cancer case in the absence of a magnetic field; F. Dose difference for the breast cancer case between the cases with and without a magnetic field |
但对于乳腺癌病例,磁场下ESE明显改变了射野外的剂量分布。对于有磁场的情况,散射到空气中的电子流会随着磁场主轴的方向飘移较长的距离,沿上方可以到达患者下颌位置,沿下方则可到达下腹部的位置。并且ESE引起的射野外剂量随着电子运动距离的增加逐渐减弱。而对于无磁场的情况,背散射回到空气中的次级电子会向四周弥散,主要影响在射野范围内,对射野外远端的影响很小。针对乳腺癌病例中下颌区域的皮肤剂量,在有磁场的情况,下颌皮肤区域1 cm3体积对应的剂量D1 cm3为454.6 cGy,为处方剂量(5 000 cGy)的9.09%。而对于无磁场的情况,下颌皮肤区域对应的剂量D1 cm3为92.5 cGy,仅为处方剂量的1.85%,见图 2。
3、添加防护膜后的ESE结果在乳腺癌病例的下颌位置虚拟放置1 cm防护膜后重新进行计算后的射野外ESE结果见图 3。从图 3可以看出,添加防护膜可以有效减少ESE对下颌皮肤剂量的影响。添加防护膜后的下颌皮肤剂量体积直方图(DVH)曲线明显优于原始计划,与无磁场计划的DVH更为接近。对于剂量学指标,原始计划中下颌皮肤区域D1 cm3为454.6 cGy,而添加有防护膜之后,可以起到很好的防护效果,下颌位置的皮肤剂量D1 cm3降为113.6 cGy,几乎与无磁场的情况相当(D1 cm3=92.5 cGy)。
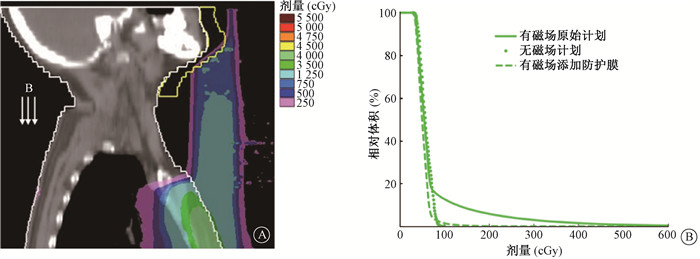
|
图 3 添加虚拟防护膜对降低乳腺癌病例磁场下ESE剂量的作用 A. 添加虚拟防护膜(图中下颌位置黄色结构)后剂量分布图;B.各计划之间的下颌皮肤DVH曲线对比 Figure 3 Effects of adding virtual protective bolus on the reduction of ESE-induced doses for the breast case in the presence of a magnetic field A. Dose distribution after adding virtual bolus (yellow structure); B. DVH curves of chin skin in three plans |
讨论
磁场的存在主要影响带电粒子的运动轨迹,而光子不带电,其与物质的相互作用几乎不受磁场影响。但光子与物质相互作用产生的次级电子会受到磁场作用而偏转。对于散射到空气中的次级电子,会在磁场作用下汇聚形成电子流,沿着(或背离)主磁场方向漂移到射野外区域。在喉癌病例中,肿瘤靶区的边缘靠近颈部皮肤,从人体出射的次级电子也在颈部皮肤附近漂移,其中大部分次级电子会受到电子回转效应的作用,重新返回颈部,导致射野内颈部皮肤剂量的升高。即使产生了一小部分空气中的ESE,也会很快被颈部皮肤所阻挡,漂移到射野外的电子很少。因此,尽管磁场作用导致喉癌病例中射野外空气中剂量分布有些许升高,但幅度很小,几乎与无磁场的情况相当。因而对于磁场下的喉癌病例,主要表现在射野内颈部皮肤剂量略微升高,ESE对射野外的剂量影响非常小。
但在乳腺癌病例的调强计划中,情况会有所不同。电子在空气中的平均自由程相对较长,如果不存在其他材料阻挡,ESE电子流将在空气中漂移到较远的距离。乳腺癌病例中的ESE电子流甚至会漂移到患者的下颌位置,造成局部皮肤剂量的显著升高。类似的研究此前在ViewRay 0.35T磁共振引导放疗系统中已经开展过,Park等[12]报道了在磁共振图像引导的乳腺癌放疗中观察到显著的电子流效应,并且报道在其中一个极端病例中,下颌皮肤最大剂量为处方剂量的16.1%,高于本文中的结果。Nachbar等[7]报道了第一例在Unity 1.5 T磁共振加速器上接受治疗的部分乳腺照射(partial breast irradiation, PBI)病例,同时也对磁场下的ERE和ESE进行了研究,并报道ESE引起下颌皮肤最大剂量约为处方剂量的6.5%, 这与本文报道的结果较为接近。可以推测,磁场强度的大小可能是影响ESE的一个因素,磁场越强,次级电子在空气中作圆周运动的半径越小,从而更容易将能量沉积在本地,导致射野外的ESE份额相对较低。而添加防护膜对于阻挡乳腺癌病例中的ESE作用非常明显,添加1 cm防护膜后的下颌皮肤剂量几乎与无磁场的情况相当。建议在MR-Linac上开展乳腺癌放疗前预先评估ESE的影响,尤其对于下颌位置,必要时可以考虑添加防护膜来予以屏蔽。
本研究的主要不足之处是缺少实验测量数据的验证,所有研究结果均来自于Monaco系统的模拟计算。而Monaco系统中Unity系统机器模型的构建、调试和验证,几乎都是针对射野内的剂量分布,很少关注射野外空气中的剂量。因此,有必要通过实验测量的手段对射野外ESE做进一步的研究,验证Monaco系统对野外ESE剂量计算的准确性,这也是下一步的研究工作。首先,从规则几何模体出发,利用固体水,构建均匀模体,利用EBT3胶片来测量不同大小照射野在射野外的ESE剂量。也将在模体入射端和出射端都进行类似的测量工作。考虑到ESE剂量一般较低,因此在使用EBT3胶片做测量验证时,需要给与足够的处方剂量,以保证胶片测量的精度。所有测量结果将与Monaco系统计算数据进行对比,分析其差别以及误差来源。其次,为了尽可能还原患者治疗时的真实场景,采用RANDO仿真人体模型来开展磁场下乳腺癌调强计划的测量研究,同样将采用EBT3胶片,验证模体外空气中ESE剂量分布,下颌区域的皮肤表面剂量。同时也可以开展针对外加防护膜的研究,通过开展在体剂量测量验证该方法的有效性。
ESE是MR-Linac系统上新发现的一种特有现象。磁场下的ESE会改变射野外剂量分布,导致局部表面剂量升高,并且在模体出射端的效应比入射端更为显著。尽管在喉癌调强计划中磁场下的ESE带来的影响很小,但在乳腺癌调强计划中,ESE会导致患者下颌皮肤剂量的增加,而外加防护膜的方法对于射野外远处的ESE能起到较好的屏蔽效果。
利益冲突 无
志谢 本研究获得了肿瘤精准放疗星火计划临床科研基金项目(HDRS2020030205)的资助
作者贡献声明 刘红冬负责方案构思、数据分析和论文撰写; 丁寿亮负责结构勾画和计划设计;阳露参与数据处理与论文撰写;王彬、李永宝参与数据准备与论文修改;黄晓延负责指导研究思路与论文修改
| [1] |
Slotman B, Gani C. Online MR-guided radiotherapy-a new era in radiotherapy[J]. Clin Transl Radiat Oncol, 2019, 18: 102-103. DOI:10.1016/j.ctro.2019.04.011 |
| [2] |
Lagendijk JJW, Raaymakers BW, Raaijmakers AJE, et al. MRI/linac integration[J]. Radiother Oncol, 2008, 86(1): 25-29. DOI:10.1016/j.radonc.2007.10.034 |
| [3] |
van Herk M, McWilliam A, Dubec M, et al. Magnetic resonance imaging-guided radiation therapy: a short strengths, weaknesses, opportunities, and threats analysis[J]. Int J Radiat Oncol Biol Phys, 2018, 101(5): 1057-1060. DOI:10.1016/j.ijrobp.2017.11.009 |
| [4] |
Winkel D, Bol GH, Kroon PS, et al. Adaptive radiotherapy: the Elekta unity MR-linac concept[J]. Clin Transl Radiat Oncol, 2019, 18: 54-59. DOI:10.1016/j.ctro.2019.04.001 |
| [5] |
Woodings SJ, Bluemink JJ, de Vries J, et al. Beam characterisation of the 1.5 T MRI-linac[J]. Phys Med Biol, 2018, 63(8): 085015. DOI:10.1088/1361-6560/aab566 |
| [6] |
Raaijmakers AJE, Raaymakers BW, Lagendijk JJW. Integrating a MRI scanner with a 6 MV radiotherapy accelerator: dose increase at tissue-air interfaces in a lateral magnetic field due to returning electrons[J]. Phys Med Biol, 2005, 50(7): 1363. DOI:10.1088/0031-9155/50/7/002 |
| [7] |
Nachbar M, M nnich D, Boeke S, et al. Partial breast irradiation with the 1.5 T MR-Linac: First patient treatment and analysis of electron return and stream effects[J]. Radiother Oncol, 2020, 145: 30-35. DOI:10.1016/j.radonc.2019.11.025 |
| [8] |
Andreozzi JM, Brůža P, Cammin J, et al. Optical imaging method to quantify spatial dose variation due to the electron return effect in an MR-linac[J]. Med Phys, 2020, 47(3): 1258-1267. DOI:10.1002/mp.13954 |
| [9] |
Shortall J, Vasquez Osorio E, Aitkenhead A, et al. Experimental verification the electron return effect around spherical air cavities for the MR-Linac using Monte Carlo calculation[J]. Med Phys, 2020, 47(6): 2506-2515. DOI:10.1002/mp.14123 |
| [10] |
游士虎, 胡南, 吴章文, 等. MRI引导放射治疗中电子回转效应的蒙特卡罗研究[J]. 原子核物理评论, 2015, 32(3): 363-367. You SH, Hu N, Wu ZW, et al. Study on the electronic return effect in the MRI guidedradiotherapy by Monte Carlo simulation[J]. Nucl Phys Rev, 2015, 32(3): 363-367. DOI:10.11804/NuclPhysRev.32.03.363 |
| [11] |
Malkov VN, Hackett SL, Wolthaus J, et al. Monte Carlo simulations of out-of-field surface doses due to the electron streaming effect in orthogonal magnetic fields[J]. Phys Med Biol, 2019, 64(11): 115029. DOI:10.1088/1361-6560/ab0aa0 |
| [12] |
Park JM, Shin KH, Kim JI, et al. Air-electron stream interactions during magnetic resonance IGRT: Skin irradiation outside the treatment field during accelerated partial breast irradiation[J]. Strahlenther Onkol, 2018, 194(1): 50-59. DOI:10.1007/s00066-017-1212-z |
| [13] |
Paudel MR, Kim A, Sarfehnia A, et al. Experimental evaluation of a GPU-based Monte Carlo dose calculation algorithm in the Monaco treatment planning system[J]. J Appl Clin Med Phys, 2016, 17(6): 230-241. DOI:10.1120/jacmp.v17i6.6455 |
| [14] |
Hissoiny S, Ozell B, Bouchard H, et al. GPUMCD: a new GPU-oriented Monte Carlo dose calculation platform[J]. Med Phys, 2011, 38(2): 754-764. DOI:10.1118/1.3539725 |
| [15] |
Hissoiny S, Raaijmakers AJE, Ozell B, et al. Fast dose calculation in magnetic fields with GPUMCD[J]. Phys Med Biol, 2011, 56(16): 5119. DOI:10.1088/0031-9155/56/16/003 |
 2021, Vol. 41
2021, Vol. 41


