2. 中山大学附属肿瘤医院, 广州 510000;
3. 安徽慧软科技有限公司, 合肥 230088
2. Sun Yat-sen University Cancer Center, Guangzhou 510000, China;
3. Anhui Wisdom Technology Co. Ltd, Hefei 230088, China
目前,临床质子放射治疗取相对生物效应(relative biological effects, RBE)为1.1[1],然而大量的实验数据证明质子RBE是可变的,而且与剂量、生物终点、组织类型和平均传能线密度(linear energy transfer,LET)等有关[2-3],忽略RBE在治疗计划中的变化,可能会导致质子治疗计划的偏差以及患者并发症的发生[4]。考虑到相对生物效应的可变性,需要提高在计划评估期间对RBE不确定性的认识,于是相对生物效应模型被开发出来用来预测质子RBE,可以分为两种,一种是基于LQ(linear quare,LQ)模型开发[5-7],以LETd为输入参数;另一种是基于DNA损伤修复模型开发[8-9],以LETt为输入参数。此前对比两种模型的研究很少。因此,本研究利用粒子模拟工具TOPAS(tool of particle simulation),重新模拟质子治疗计划并对比两种模型计算的生物剂量,最后与传统临床质子生物剂量做比较。该研究为质子治疗系统面临的RBE模型选择问题提供参考,促进质子可变生物效应在临床治疗计划中的应用。
材料与方法1.蒙特卡罗模拟设置:TOPAS是一款专门用于质子治疗的蒙特卡罗模拟软件[10]。本研究使用TOPAS Version: 3.3.p1版本。该版本基于GEANT4.10.1蒙特卡罗软件的截面库。物理模块采用了GEANT4的模块化物理模型,模型具体包括:标准电磁模型、高精度BIC模型、衰变模型、离子簇射模型、弹性碰撞模型与非弹性碰撞模型。本套模型已经经过理论和实验验证,尤其适用于质子模拟[10-11]。为提高TOPAS模拟计算的效率,EM(expectation maximization,EM)模型的最大和最小能量分别设置为300 MeV和100 eV。对质子、α粒子、光子、电子等次级粒子的射程截断设置为0.05 mm。
本次在水箱中模拟时采用的质子源是扩展布拉格峰质子束(spread out Bragg peak, SOBP),具体信息如下:沿着水模体x方向入射,平均能量为200 MeV,射程为21 cm,调制宽度为11 cm,模拟的总粒子数约为1.28×108。模拟临床质子治疗计划时,束流模型参考了刘红冬[12]构建的IBA质子加速器束流模型,质子束的实际位置、发射方向等通过RT PLAN获得。
所有的模拟计算均在一台服务器工作站上完成(CPU×2: Intel Xeon E5-2698 V4×2 3.20 GHz, 16×2=32 threads, RAM: 64 GB, OS: CentOS release 6.9),完成单次模拟所需的时间为10~48 h。水箱中模拟时在布拉格峰位置以内结果的统计误差控制在0.1%以内,而峰前和峰后位置的低剂量结果统计误差控制在5.0%以内。脑部肿瘤和前列腺肿瘤在高剂量区的统计误差控制在2.0%以内,在低剂量区的统计误差控制在5.2%以内。这些误差在可接受范围内,保证了模拟的可信度。
2. 模体
(1) 水箱: 大小为30 cm×1 cm×1 cm,因为只研究中心轴线的深度生物剂量分布,模型只沿着深度按照0.1 cm的精度细分,材料定义为TOPAS自带的G4 _ WATER,平均激发能为78 eV,同时为了避免对束流的影响,模体以外的空间设置为真空。
(2) 患者模体: 患者数据来自在UFHPTI的临床放疗计划,均采取笔形束扫描的治疗方式。其中脑部肿瘤病例单次照射剂量为250 cGy。体模122 mm ×202 mm×167 mm,体素0.976 562 5 mm× 0.976 562 5 mm×1 mm,机架角度分别是90°和180°,每个角度的质子束总数为193和138。前列腺肿瘤病例单次照射剂量为200 cGy。体模282 mm×116 mm×157 mm,体素1.171 875 mm× 1.171 875 mm×1 mm,机架角度分别是90°和270°,每个角度的质子束总数为1 624和1 626。
3. LETd和LETt:LET的定义有两种,一种是LETd,另一种是LETt。目前计算这两种平均LET的方法有很多,在TOPAS中采用了以下平均LET的定义[13]:
LETt为通过将质子局部沉积的能量与每个步骤中产生的二次电子的动能相加来逐步计数,计算公式如下:
| $ \mathrm{LET}_{\mathrm{t}}=\frac{\sum\limits_{i}^{n} d x_{i} \times \mathrm{LET}_{i}}{\sum\limits_{i}^{n} d x_{i}} $ | (1) |
式中,i为第i个粒子;n为体素中粒子的总数;dxi为第i个粒子的路径长度,mm;LETi为第i个粒子在体素中沉积的能量除以步长,keV/μm。
LETd为每个粒子的LETi根据其对每个体素局部剂量的贡献进行加权,计算公式如下:
| $ \mathrm{LET}_{\mathrm{d}}=\frac{\sum\limits_{i}^{n} E_{d e p, i} \times \mathrm{LET}_{i}}{\sum\limits_{i}^{n} E_{d e p, i}} $ | (2) |
式中,Edep, i为每步在体素中沉积的能量,MeV。
4. 生物剂量计算方法:计算传统临床质子生物剂量时,相对生物效应统一取1.1,即:
方法1:
| $ Dose _{1.1}= Dose \times 1.1 $ | (3) |
方法2:
| $ {Dose}_{\mathrm{LET}_{\mathrm{d}}}={Dose}\left(1+c \mathrm{LET}_{\mathrm{d}}\right)= Dose \mathrm{RBE}_{\mathrm{LET}_{\mathrm{d}}} $ | (4) |
方法2是基于LQ模型开发得到, 也叫现象学模型(phenomenological model, PM)。该模型假设放射性敏感度参数α近似与LETd呈线性增加,放射性敏感度参数β对LETd不具有影响[14-15]。式中,c是一个拟合参数,通过体外实验数据拟合得到。在这项工作中,方法2使用了c=0.04 μm ·keV-1的值,这是通过引入对组织α/β比率、治疗计划的剂量和LET进一步细化c以更好地接近基础生物学得到的数值[6]。
方法3:
| $ Dose _{\mathrm{LET}_{\mathrm{t}}}= Dose \left(d \mathrm{LET}_{\mathrm{t}}+e\right) f / \gamma_{r}= Dose R B E_{\mathrm{LET}_ \mathrm{t}} $ | (5) |
方法3是基于DNA损伤修复模型开发得到。该模型通过蒙特卡罗方法模拟质子照射细胞核之后的DNA损伤,包括DNA断裂、错修复和未修复量,得到细胞损伤与LETt近似是线性关系(R2>0.9),模型中的参数通过拟合的方式得到[16]。式中,d= 1.149 μm ·keV-1 ·Gy-1,e=24.1 Gy-1,f=0.073 6,γr=1.726 Gy-1。
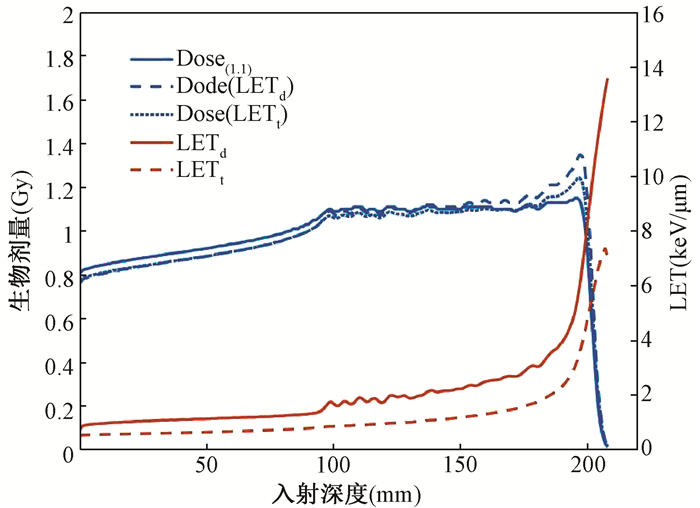
结果1. 水箱计算结果:水箱中两种平均LET和不同方法计算的生物剂量随水深度的变化示于图 1。由图 1可知,方法2、3计算的生物剂量大小有差异,但变化趋势一致。在质子束入射区,方法1计算的生物剂量要大于其他两种方法计算的生物剂量。在剂量坪区初,3种计算方法的生物剂量大致相同,但是到了剂量坪区中间,方法2计算的生物剂量曲线出现上升趋势,并大于其他两种计算方法。到了射程末端,方法2、3计算出来的生物剂量出现陡增,并远远大于方法1。
|
图 1 水箱中生物剂量与两种平均LET计算结果 Figure 1 Calculation results of biological dose and two kinds of LET in water phantom |
2. 临床病例计算结果
(1) 脑部肿瘤:脑部肿瘤的计算结果示于图 2。TOPAS模拟患者模体的物理剂量与治疗计划物理剂量分布吻合较好,所在平面3 mm/3%的γ通过率为95.2%。方法1、2、3计算的最大生物剂量均出现在靶区,分别是272.73、334.62和334.72 cGy。而靶区外的生物剂量均 < 100 cGy。方法2、3计算的生物剂量相对差异均 < 5%,与方法1的生物剂量相对差异均 < 25%。

|
图 2 脑部肿瘤计算结果A. TOPAS模拟剂量;B. 传统临床生物剂量(Dose1.1);C. 方法2计算的生物剂量(DoseLETd;D. 方法3计算的生物剂量DoseLETt Figure 2 Calculated dose maps of brain tumor A. Physical dose simulated by TOPAS; B. Traditional clinical biological dose (Dose1.1; C. Biological dose calculated using method 2 (DoseLETd); D. Biological dose calculated using method 3(DoseLETt) |
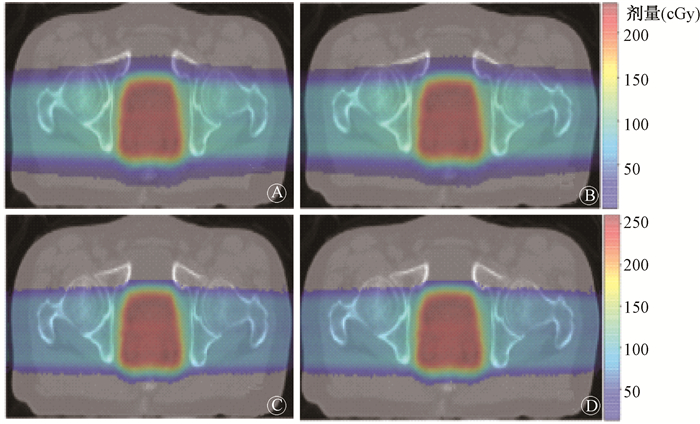
(2) 前列腺肿瘤:前列腺肿瘤的计算结果示于图 3。TOPAS模拟患者模体的物理剂量分布与治疗计划物理剂量分布吻合较好,所在平面3 mm/3%的γ通过率为96.5%。方法2、3计算的最大生物剂量同样出现在靶区,分别为219.56、245.51、239.52 cGy,而靶区外的生物剂量均 < 95 cGy。方法2、3计算的生物剂量相对差异均 < 4%,与方法1的生物剂量相对差异均 < 12%。
|
图 3 前列腺肿瘤计算结果A. TOPAS模拟剂量;B. 传统临床生物剂量(Dose1.1);C. 方法2计算的生物剂量(DoseLETd;D. 方法3计算的生物剂量DoseLETt Figure 3 Calculated dose maps of prostate tumor A. Physical dose simulated by TOPAS; B. Traditional clinical biological dose (Dose1.1; C. Biological dose calculated using method 2 (DoseLETd); D. Biological dose calculated using method 3(DoseLETt) |
为了量化3种方法计算的生物剂量差异,根据剂量大小选取3个参考点D1、D2和D3,其中D1在靶区外,约为最大剂量的40%;D2在靶区内,为最大剂量点;D3在入口处,约为最大剂量的20%。统计3个参考点的物理剂量、LET值、RBE值和生物剂量,具体信息见表 1。从表 1可知,与方法1相比较,方法2和3在靶区内的点差异很大,而靶区外的点差异较小。对于脑部肿瘤,方法2靶区内点的差异为71.99 cGy,相对差异为26.36%;方法3在靶区内点的差异为61.91 cGy,相对差异为22.73%。对于前列腺肿瘤,方法2在靶区内的点的差异为25.95 cGy,相对差异为11.82%;方法3在靶区内的点的差异为19.96 cGy,相对差异为9.09%。对比方法2和3发现靶区内外点的差异均很小,脑部和前列腺肿瘤最大差异分别是9.92和5.99 cGy。
|
|
表 1 参考点物理量 Table 1 The physical parameters of reference points |
讨论
充分发挥质子放疗的潜力是放射治疗领域的一个重大挑战,尤其是将可变相对生物效应应用到临床中。本研究使用基于LET的RBE模型评估质子生物剂量,结果显示两种生物模型差异性较小,与传统临床质子生物剂量相比较时发现在靶区内有很大的差异,这说明传统临床质子治疗保守地估计了生物效应,可能忽略了生物效应热点。
除了基于LET的RBE模型可以预测RBE,Kase等[17]用微剂量学预测质子RBE,即通过线能(yd)的分布来预测RBE。与此相比,本研究在入射区域和靶区内的结果相差不大,但射束末端明显降低(微剂量学最大RBE为2.20,方法2为1.75,方法3为1.66)。原因是Kase等[17]计算的α值小于方法2与方法3,而α值越小,RBE越大[18]。McNamara等[19]此前基于全球的体外实验数据对比了不同现象学模型计算的RBE,发现现象学模型预测的RBE在质子射程内均大于1.1。本研究结果与其略有不同,可能的原因是采用不同的LET计算方法和物理模块。
此前的研究大多数利用现象学模型计算RBE,并未考虑生物剂量,而本研究利用现象学模型计算了生物剂量。Smith等[20]利用DNA损伤修复模型计算脑部肿瘤的生物剂量时发现高生物剂量位于靶区内。本研究结果与其相吻合。
本研究尚有一些不足之处,首先是选取的病例较少,存在一定的偶然性,后续研究应当选取更多病例分析。其次是病例部位不同,未能分析危及器官的生物剂量。尽管如此,本研究基于有限的数据对比了两种不同机制生物模型计算的生物剂量,为未来质子治疗计划系统的相对生物效应模型选择问题提供了参考。
利益冲突 无本研究由署名作者按以下贡献声明独立开展,未因进行该研究接受任何不正当的职务或财务利益,在此对研究的独立性和科学性予以保证
作者贡献声明 陶寅负责实验和撰写论文;张增鹏、刘红冬负责数据的收集和分析;裴曦、徐榭、陈志指导研究设计和论文修改
| [1] |
Fager M, Toma-Dasu I, Kirk M, et al. Linear energy transfer painting with proton therapy: a means of reducing radiation doses with equivalent clinical effectiveness[J]. Int J Radiat Oncol Biol Phys, 2015, 91(5): 1057-1064. DOI:10.1016/J.IJROBP.2014.12.049 |
| [2] |
Jr DL, Wambersie A, Whitmore G. Prescribing, recording and reporting proton-beam therapy[J]. ICRU, 2007, 7(2): 1-210. DOI:10.1093/jicru_ndm021 |
| [3] |
Paganetti H, Niemierko A, Ancukiewicz, et al. Relative biological effectiveness (RBE) values for proton beam therapy[J]. Int J Radiat Oncol Biol Phys, 2002, 53(2): 407-421. DOI:10.1088/0031-9155/59/22/R419 |
| [4] |
Peeler CR, Mirkovic D, Titt U, et al. Clinical evidence of variable proton biological effectiveness in pediatric patients treated for ependymoma[J]. Radiother Oncol, 2016, 121(3): 395-401. DOI:10.1016/j.radonc.2016.11.001 |
| [5] |
Wedenberg M, Toma-Dasu I. Disregarding RBE variation in treatment plan comparison may lead to bias in favor of proton plans[J]. Med Phys, 2014, 41(9): 9-17. DOI:10.1118/1.4892930 |
| [6] |
McMahon SJ, Paganetti H, Prise KM. LET-weighted doses effectively reduce biological variability in proton radiotherapy planning[J]. Phys Med Biol, 2018, 63(22): 22-32. DOI:10.1088/1361-6560/aae8a5 |
| [7] |
Unkelbach J, Botas P, Giantsoudi D, et al. Reoptimization of intensity modulated proton therapy plans based on linear energy transfer[J]. Int J Radiat Oncol Biol Phys, 2016, 15: 1097-1106. DOI:10.1016/j.ijrobp.2016.08.038 |
| [8] |
Henthorn NT, Warmenhoven JW, Sotiropoulos M, et al. Nanodosimetric simulation of direct ion-induced DNA damage using different chromatin geometry models[J]. Radiat Res, 2017, 188(6): 690-703. DOI:10.1667/RR14755.1 |
| [9] |
Warmenhoven JW, Henthorn NT, Ingram SP, et al. Insights into the non-homologous end joining pathway and double strand break end mobility provided by mechanistic in silico modelling[J]. DNA Rep, 2020, 85: 1568-7864. DOI:10.1016/j.dnarep.2019.102743 |
| [10] |
Perl J, Shin J, Schümann J, et al. TOPAS: an innovative proton monte carlo platform for research and clinical applications[J]. Med Phys, 2012, 39(11): 6818-6837. DOI:10.1118/1.4758060 |
| [11] |
Polster L, Schuemann J, Rinaldi I, et al. Extension of TOPAS for the simulation of proton radiation effects considering molecular and cellular endpoints[J]. Phys Med Biol, 2015, 60(13): 5053-5070. DOI:10.1088/0031-9155/60/13/5053 |
| [12] |
刘红冬. 基于蒙特卡罗算法的质子放疗独立剂量验证方法与系统研究[D]. 合肥: 中国科学技术大学出版社, 2019. Liu HD. The method and system of independent dose verification of proton radiotherapy based on Monte Carlo algorithm[D]. Hefei: China University of Science and Technology Press, 2019. |
| [13] |
Granville DA, Sawakuchi GO. Comparison of linear energy transfer scoring techniques in Monte Carlo simulations of proton beams[J]. Phys Med Biol, 2015, 60(14): 65-76. DOI:10.1088/0031-9155/60/14/N283 |
| [14] |
Wilkens JJ, Oelfke U. A phenomenological model for the relative biological effectiveness in therapeutic proton beams[J]. Phys Med Biol, 2004, 49(13): 2811-2825. DOI:10.1088/0031-9155/49/13/004 |
| [15] |
Carabe-Fernandez A, Dale RG, Hopewell JW, et al. Fractionation effects in particle radiotherapy: implications for hypo-fractionation regimes[J]. Phys Med Biol, 2010, 55(19): 5685-5700. DOI:10.1088/0031-9155/55/19/005 |
| [16] |
Henthorn NT. In silico non-homologous end joining following ion induced DNA double strand breaks predicts that repair fidelity depends on break density[J]. Sci Reports, 2018, 8(1): 2654-2663. DOI:10.1038/s41598-018-21111-8 |
| [17] |
Kase Y, Yamashita W, Matsufuji N, et al. Microdosimetric calculation of relative biological effectiveness for design of therapeutic proton beams[J]. Radiat Res, 2013, 54(3): 485-493. DOI:10.1093/jrr/rrs110 |
| [18] |
Giantsoudi D, Grassberger C, Craft D, et al. Linear energy transfer-guided optimization in intensity modulated proton therapy: feasibility study and clinical potential[J]. Int J Radiat Oncol Biol Phys, 2013, 87(1): 216-222. DOI:10.1016/j.ijrobp.2013.05.013 |
| [19] |
McNamara AL, Schuemann J, Paganetti H. A phenomenological relative biological effectiveness (RBE) model for proton therapy based on all published in vitro cell survival data[J]. Phys Med Biol, 2015, 60(21): 8399-8416. DOI:10.1088/0031-9155/60/21/8399 |
| [20] |
Smith EAK, Henthorn NT, Warmenhoven JW, et al. In silico models of DNA damage and repair in proton treatment planning: a proof of concept[J]. Sci Rep, 2019, 9(1): 19-26. DOI:10.1038/s41598-019-56258-5 |
 2021, Vol. 41
2021, Vol. 41


