2. 中国疾病预防控制中心辐射防护与核安全医学所 辐射防护与核应急中国疾病预防控制中心重点实验室, 北京 100088
2. Key Laboratory of Radiological Protection and Nuclear Emergency, China CDC, National Institute for Radiological Protection, Chinese Center for Disease Control and Prevention, Beijing 100088, China
同步辐射是高能带电粒子在电磁场作用下沿弯转轨道行进时所发出的辐射,可产生从远红外到X光波段的光谱,具有高亮度、高纯净、宽波段、高准直等特点;同步辐射光源已经成为支撑多学科前沿研究及众多国家需求的国家重大科技基础设施[1-4]。自20世纪70年代以来,国际上大约每隔十几年就会出现一批新的性能更好的同步辐射光源[1]。我国第4代同步辐射光源预计电子能量高达到6 GeV,如此高能射线装置,其辐射防护非常关键。高能同步辐射光源一般包括直线加速器、低能输运线、增强器(同步加速器)、高能输运线(储存环注入区)、储存环、光束线站及其配套设施。电子枪产生电子,电子由直线加速器加速到几百MeV,经过低能输运线注入到增强器,再把电子束加速到储存环所需要的能量几个GeV;储存环是将通过高能输运线输送、注入的几个GeV电子束团进行储存和绕环运动,使其在绕环运动时产生同步辐射光(几十~几百keV),并通过光束线引出到各自的实验站进行实验[5-6]。在同步加速器、储存环注入区和储存环电子能量达到最高,束流损失较大,辐射屏蔽难度最大,本文重点研究和讨论储存环、储存环注入区(高能输运线)和同步加速器的屏蔽计算。
材料与方法1. 研究对象:本研究高能同步辐射光源的同步加速器为近似圆形,周长为450 m;高能输运线长度为100 m;储存环呈圆形锯齿状,周长为1 400 m,锯齿区域对应同步辐射光引出区;以上3个区域均采用地上隧道设计,隧道采用混凝土作为屏蔽材料,密度为2.4 g/cm3,引出区增加铅屏蔽材料,密度为11.3 g/cm3。
储存环隧道外侧屏蔽墙厚度为90 cm,内侧屏蔽墙厚度为70 cm,顶部屏蔽厚度为80 cm;电子束流管距离外侧墙最近距离为120 cm,距内侧墙最近距离为280 cm,距顶部的距离为230 cm,高度为100 cm。储存环锯齿墙距靶的距离为3 448 cm,屏蔽材料为100 cm厚混凝土和15 cm厚铅。
储存环注入区隧道外侧屏蔽墙厚度为150 cm,内侧屏蔽墙厚度为120 cm,顶部屏蔽厚度为120 cm;电子束流管距离外侧墙最近距离为170 cm,距内侧墙最近距离为430 cm,距顶部的距离为230 cm,高度为100 cm。
同步加速器隧道两侧屏蔽墙和顶的厚度均为50 cm,电子束流管距离外侧墙距离为120 cm,距内侧墙距离为230 cm,距顶部的距离为230 cm,高度为100 cm。
2. 材料:本研究中使用的模拟计算工具是FLUKA[7],版本FLUKA 2011.2x.2,FLUKA是一个开放的通用集成粒子物理蒙特卡罗仿真软件包。
3. 计算方法
(1) Jenkins公式[8-9]:当电子打厚靶时,主要考虑在靶与屏蔽体外剂量计算点连线与束流的夹角20°~160°方向的辐射,采用Jenkins公式[8-9]计算电子产生的光子周围剂量当量Hγ和中子周围剂量当量Hn,计算公式如下:
| $ \begin{array}{l} {H_\gamma } ={10^{ - 13}}{E_0}{\left( {\frac{{{\rm{sin}}\theta }}{{a + d}}} \right)^2} \times \\ \left[ {\frac{{133{{\rm{e}}^{ - \frac{\mu }{\rho }\frac{{\rho d}}{{{\rm{sin}}\theta }}}}}}{{{{(1 - 0.98{\rm{cos}}\theta )}^2}}} + 0.267{e^{ - \frac{{\rho d}}{{{\lambda _1}{\rm{sin}}\theta }}}}} \right] \end{array} $ | (1) |
| $ \begin{array}{l} {H_n} ={10^{ - 13}}{E_0}{\left( {\frac{{{\rm{sin}}\theta }}{{a + d}}} \right)^2} \times \left[ {\frac{{{{\rm{e}}^{ - \frac{{\rho d}}{{{\lambda _1}{\rm{sin}}\theta }}}}}}{{{{(1 - 0.72{\rm{cos}}\theta )}^2}}} + } \right.\\ \;\;\;\;\;\left. {\frac{{\;10{{\rm{e}}^{ - \frac{{\rho d}}{{{\lambda _3}{\rm{sin}}\theta }}}}}}{{(1 - 0.75{\rm{cos}}\theta )}} + 3.79{z^{0.73}}{{\rm{e}}^{ - \frac{{\rho d}}{{{\lambda _2}{\rm{sin}}\theta }}}}} \right] \end{array} $ | (2) |
式中,Hr当光子周围剂量当量,Sv/e;Hn为中子周围剂量当量,Sv/e;E0为入射电子能量,GeV;θ为靶与屏蔽体外剂量计算点连线与束流的夹角,°;a为靶到屏蔽体内表面的距离,cm;d为屏蔽体厚度,cm;Z为靶原子序数;ρ为屏蔽材料的密度,g/cm3;μ为屏蔽材料对光子的衰减系数,cm-1,μ=0.056 cm-1(混凝土);λ1为屏蔽材料对高能中子的吸收长度,g/cm2,λ1=120 g/cm2(混凝土);λ2为屏蔽材料对中能中子的吸收长度,g/cm2,λ2=55 g/cm2(混凝土);λ3为屏蔽材料对低能中子的吸收长度,g/cm2,λ3=30 g/cm2(混凝土)。
(2) Sakano公式[10]:当电子打薄靶时,主要考虑在靶与屏蔽体外剂量计算点连线与束流的夹角约0°方向的辐射(对应同步辐射光引出的锯齿墙区域),一般采用Sakano公式[10]计算由单个电子打靶产生的剂量当量H(d, a, ω):
| $ \begin{array}{l} H\left( {d, a, \omega } \right) ={H_0}{{\rm{e}}^{ - 0.19 \times (\omega - 1.0)}} \times \\ \;\;\;\;\;\;\;\;\;\;\;{a^{ - 2}} \times {\left( {\frac{{{E_0}}}{{100}}} \right)^{1.47}}{{\rm{e}}^{ - \frac{\mu }{\rho }\rho d}} \end{array} $ | (3) |
式中,E0为入射电子能量,MeV;H0=1×10-12,E0>200 MeV;ω为电子在靶中的径迹长度,ω =t/sinϕ;t为靶的厚度,cm;ϕ为靶表面与束流夹角;a为靶到屏蔽体内表面的距离,m;μ为屏蔽材料的衰减系数,cm-1,μ=0.052 cm-1(混凝土);d为屏蔽体厚度,cm;ρ为混凝土的密度,g/cm3。
当使用混凝土和铅两种材料屏蔽时,单个电子打靶产生的剂量当量H(d, a, ω)参照下式进行计算[10-11]:
| $ \begin{array}{l} H\left( {d, a, \omega } \right) ={H_0}{{\rm{e}}^{ - 0.19 \times (\omega - 1.0)}} \times \\ {a^{ - 2}} \times {\left( {\frac{{{E_0}}}{{100}}} \right)^{1.47}}{{\rm{e}}^{ - \frac{\mu }{\rho }\rho d}} \times {10^{ - {d_{{\rm{Pb}}}}/{\rm{TVL}}}} \end{array} $ | (4) |
式中,dPb为铅的厚度;TVL为铅的1/10值层,保守取TVL=5.7 cm[10-11]。
(3) 蒙特卡罗模拟:本研究采用FLUKA程序来构建同步加速器和储存环的几何结构,在几何空间和屏蔽体的构建上是基于我国拟建某高能同步辐射光源的设计,几何结构和屏蔽参数定义描述同本文研究对象中的描述。电子束的靶分别定义为厚靶和薄靶,材料为铜(密度8.9 g/cm3),厚靶定义为30 cm× 30 cm×30 cm,薄靶定义为30 cm×30 cm×2 cm。模拟的束流损失为集中损失模式(点损失),电子能量设为6 GeV,模拟的电子数为1×107个。
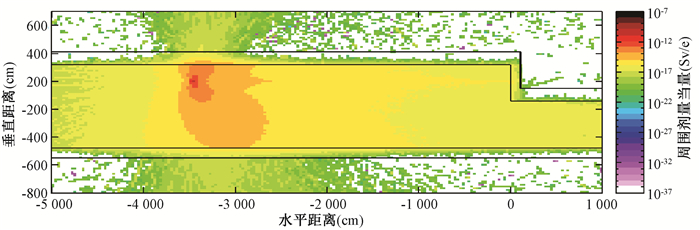
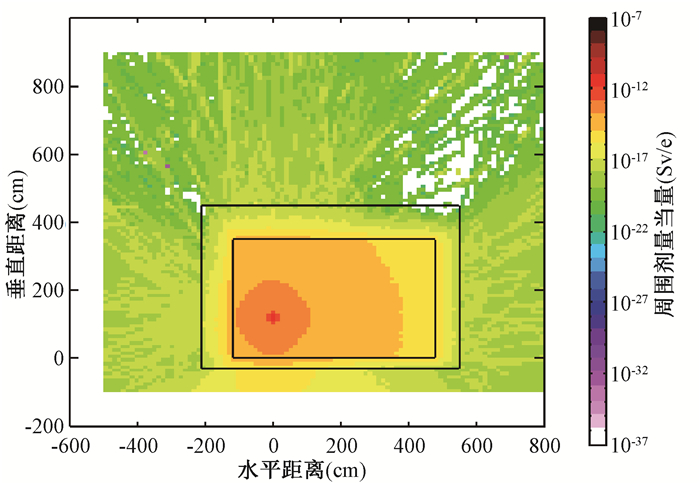
结果1. 储存环及其注入区屏蔽计算:储存环及其注入区隧道外半经验公式和蒙特卡罗模拟计算得到的单电子产生的周围剂量当量见表 1。从表 1中可以看出,根据Jenkins公式[8-9]计算得到储存环隧道外的剂量为(1.95~2.65)×10-17 Sv/e,储存环注入区隧道外的剂量为(0.918~2.50)×10-18 Sv/e;模拟计算结果分别为(1.45~1.76)×10-17 Sv/e和(0.83~1.75)×10-18 Sv/e;储存环蒙特卡罗模拟剂量分布平面图和剖面图分别见图 1和图 2。
|
|
表 1 储存环屏蔽计算参数和单电子产生的周围剂量当量 Table 1 Shielding calculation parameters of storage ring and ambient dose equivalent produced by single electron |
|
图 1 储存环单电子打厚靶产生的中子和光子周围剂量当量平面图 Figure 1 Plane distribution of neutron and photon ambient dose equivalent for single electron impinging on thick target along storage ring |
|
图 2 储存环单电子打厚靶产生的中子和光子周围剂量当量剖面图 Figure 2 Profile distribution of neutron and photon ambient dose equivalent for single electron impinging on thick target along storage ring |
从表 1中可以得出,Jenkins公式[8-9]计算的周围剂量当量与模拟计算结果的6组数据比值分别为1.51、1.53、1.34、1.11、1.20和1.43,比值比较接近,且Jenkins公式[8-9]计算的结果均略大于蒙特卡罗计算结果。
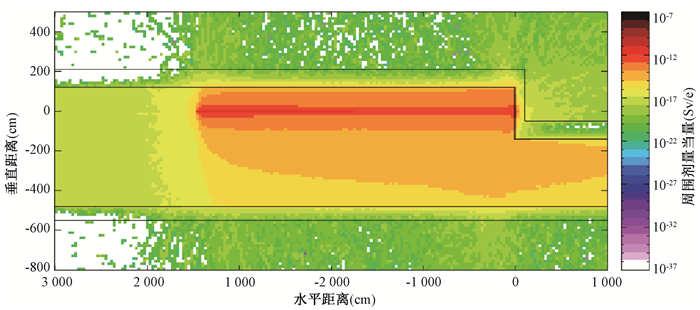
根据Sakano公式[10]计算得到同步辐射光引出锯齿墙外周围剂量当量率结果为6.62×10-17 Sv/e;蒙特卡罗模拟剂量分布平面图见图 3,模拟结果为3.30×10-17 Sv/e,Sakano公式[10]计算结果大于模拟计算结果,其值是模拟计算结果的2.01倍。
|
图 3 储存环中单电子打薄靶产生的中子和光子周围剂量当量平面图 Figure 3 Plane distribution of neutron and photon ambient dose equivalent for single electron impinging on thin target along the storage ring |
2. 同步加速器辐射屏蔽计算:同步加速器不涉及同步辐射光的引出,同步加速器隧道的屏蔽计算仅使用Jenkins公式[8-9],同步加速器隧道外半经验公式和蒙特卡罗模拟计算得到的单电子产生的周围剂量当量见表 2。从表 2中可以看出,半经验公式计算的同步加速器隧道两侧单电子产生的辐射剂量(1.05~2.85)×10-17 Sv/e,蒙特卡罗模拟的同步加速器隧道两侧单电子产生的辐射剂量(0.82~1.97)×10-17 Sv/e。从表 2可以得出,Jenkins公式[8-9]计算的周围剂量当量与模拟计算结果的3组数据比值分别为1.45、1.28和1.28,比值比较接近,且Jenkins公式[8-9]计算的结果均略大于蒙特卡罗计算结果。
|
|
表 2 同步加速器屏蔽计算参数和单电子产生的周围剂量当量 Table 2 Shielding calculation parameters of synchrotron and ambient dose equivalent produced by single electron |
讨论
本研究以高能光源储存环和同步加速器屏蔽计算为例,计算了在点损失模式下电子打厚靶和薄靶两种模式下的隧道外的辐射水平。对于厚靶模式,在束流方向约90°方向辐射水平最高。对于仅用混凝土1种材料作为屏蔽材料的隧道,Jenkins公式[8-9]计算结果与蒙特卡罗模拟结果总体比较接近,6组数据比值范围为1.11~1.53。
对于电子打薄靶模式,同步辐射光引出方向(即θ~0°)的屏蔽计算,Sakano公式[10]计算结果是蒙特卡罗模拟结果的2倍。分析原因,一是可能与模拟时采用的薄靶厚度有一定关联[10];二是在0°方向上为两种屏蔽材料,即混凝土和铅,屏蔽对象为中子和光子,而铅对中子和光子的屏蔽效果与其能量密切相关[11-12],因此导致Sakano公式[10]结果产生了差异,关于铅的1/10值层及其防护最优化需要下一步详细研究。
对加速后电子能量在GeV量级的各种电子加速器的屏蔽计算[8],尤其是对于仅采用单一屏蔽材料(如混凝土)屏蔽体的辐射水平计算,用Jenkins公式[8-9]计算是快速、保守且可行的。但当采用多种屏蔽材料时,由于受中子、光子能量及其1/10值层的影响,宜采用蒙特卡罗模拟方法。另外,对于均匀损失模式,理论上可以把均匀损失简化很多个点损失,简化模式及简化后计算的辐射水平结果的一致性将在以后的研究进行深入研究。
利益冲突 本研究未因进行该研究而接受任何不正当的职务或财务利益,在此对研究的独立性和科学性予以保证
作者贡献声明 张震设计研究方案及论文起草;王雪涛、陈飞、李玉文参与数据验算和论文修改;侯长松、练得幸、朱卫国参与建模和论文修改
| [1] |
李宜展, 樊潇潇, 曾钢, 等. 同步辐射光源的科技发展及科学影响分析——以欧洲同步辐射光源为例[J]. 世界科技研究与发展, 2019, 41(1): 19-34. Li YZ, Fan XX, Zeng G, et al. The development of synchrotron radiation sources and its influence on science and technology - A case study of synchrotron radiation source in Europe[J]. World SCI-TECH R&D, 2019, 41(1): 19-34. DOI:10.16507/j.issn.1006-6055.2018 |
| [2] |
尚智丛, 陈晨. 国家目标对大科学装置发展的影响——以美国康奈尔同步辐射光源为例[J]. 自然辩证法研究, 2010(12): 56-63. Shang ZC, Chen C. The influence of national goals on the development of large scientific devices - A case study of Cornell synchrotron radiation source[J]. Stud Dialect Nat, 2010(12): 56-63. |
| [3] |
王贻芳. 从BEPC到CEPC[J]. 现代物理知识, 2018, 30(5): 62-66. Wang YF. From BEPC to CEPC[J]. Mod Phys, 2018, 30(5): 62-66. DOI:10.13405/j.cnki.xdwz.2018.05.015 |
| [4] |
曾昭权. 同步辐射光源及其应用研究综述[J]. 云南大学学报, 2007, 30(5): 477-483. Zeng ZQ. Review of synchrotron radiation source and its application[J]. J Yunnan Univers, 2007, 30(5): 477-483. DOI:10.3321/j.issn:0258-7971.2008.05.009 |
| [5] |
王沿东, 张哲维, 李时磊, 等. 同步辐射高能X射线衍射在材料研究中的应用进展[J]. 中国材料进展, 2017, 36(3): 168-174. Wang YD, Zhang WZ, Li SL, et al. Application of synchrotron-based high-energy X-ray diffraction in materials research[J]. Mater China, 2017, 36(3): 168-174. DOI:10.7502/j.issn.1674-3962.2017.03.01 |
| [6] |
曹飞, 王同敏. 同步辐射成像技术在金属材料研究中的应用[J]. 中国材料进展, 2017, 36(3): 161-167. Chao F, Wang TM. Applications of synchrotron radiation imaging technology in metallic materials research[J]. Mater China, 2017, 36(3): 161-167. DOI:10.7502/j.issn.1674-3962.2017.03.02 |
| [7] |
Nemati MJ, Amrollahi R, Habibi M. Analysis for radiation and shielding dose in plasma focus neutron source using FLUKA[J]. J Fusion Energy, 2012, 31(3): 284-297. DOI:10.1007/s10894-011-9454-8 |
| [8] |
Jenkins TM. Neutron and photon measurements through concrete from a 15 GeV electron beam on a target-Comparison with models and calculations[J]. Nucl Instrum Methods, 1979, 159(2-3): 265-288. DOI:10.1093/oxfordjournals.rpd.a081048 |
| [9] |
李夏, 金潇. 某同步辐射光源辐射场特性研究[J]. 中国辐射卫生, 2015, 24(3): 48-51. Li X, Jin X. Study on the radiation field characteristics of a synchrotron radiation source[J]. Chin J Radiol Health, 2015, 24(3): 48-51. DOI:10.13491/j.cnki.issn.1004-714x.2015.03.017 |
| [10] |
Sakano M, Hirayama H, Ban S. Calculations of dose equivalents due to stray radiation from a high energy electron beam in a forward direction[J]. Radiat Prot Dosim, 1991, 37(3): 165-173. DOI:10.1093/oxfordjournals.rpd.a081048 |
| [11] |
International Atomic Energy Agency. IAEA Safety Report Series No.47 Radiation protection in the design of radiotherapy facilities[R]. Vienna: IAEA, 2006.
|
| [12] |
朱卫国, 梁婧, 侯长松, 等. 质子加速器治疗室辐射防护优化研究[J]. 中华放射医学与防护杂志, 2019, 39(9): 707-710. Zhu WG, Liang J, Hou CS, et al. Study on the optimization of radiation protection for therapeutic proton synchrotron[J]. Chin J Radiol Med Prot, 2019, 39(9): 707-710. DOI:10.3760/cma.j.issn.0254-5098.2019.09.013 |
 2021, Vol. 41
2021, Vol. 41


