近年来重离子束由于其在布拉格峰附近具有较高的相对生物学效应(relative biological effectiveness,RBE)等生物学特性,在肿瘤外照射放射治疗领域展现了较强的优势[1-2]。在重离子放疗过程中,RBE的确定非常重要。获取重离子的微剂量谱是常用RBE计算模型中的关键环节[3-5]。目前国内外有多种用于微剂量测量的探测器,常见的主要有组织等效正比计数器(tissue equivalent proportional counter,TEPC)[6-8]、气体电子倍增器(gas electron multiplier,GEM)-TEPC[9]及半导体探测器。绝缘体上硅(silicon on insulator,SOI)微剂量计是一种半导体探测器[10],因具有结构简单、便携、低噪声、无需高压等优点,在进行碳离子束微剂量谱测量中拥有一定的优势[11-12]。近年来,国际上使用以上探测器对质子和重离子束流、光子和中子射线均开展了微剂量谱的测量实验[13-19]。本研究使用SOI硅微剂量计对兰州重离子国家实验室提供的被动式散射束流进行了微剂量测量,从而得到不同聚甲基丙烯酸甲酯(PMMA)深度处的微剂量谱及RBE随深度变化的曲线。
材料与方法 1、微剂量测量基本物理量不管是SOI硅微剂量计,还是TEPC,测量的都是线能(lineal energy,y)。线能定义为在一个给定小体积中,由单次能量沉积事件造成的授予能ε与穿过该小体积的各向同性弦长平均值 <l >的比值:
| $ y = \frac{\varepsilon }{{ < \overline l > }} $ | (1) |
式中,ε为一次能量沉积事件中授予某一给定小体积的能量,keV;<l>为该体积内的平均弦长,μm。
线能y附近的单位线能间隔内的剂量概率密度函数为d(y),称为线能的剂量概率密度,如公式(2)所示:
| $ {\rm{d}}\left( y \right) = {\rm{ }}\frac{{yf\left( y \right){\rm{ }}}}{{\int_{_0}^{^\infty } {yf\left( y \right){\rm{d}}y} }} $ | (2) |
式中,f(y)dy为线能在y~y+dy之间的吸收剂量占总吸收剂量的分数。
剂量概率密度d(y)的期望值yD,称为剂量平均线能,y的期望值yF称为频率平均线能,如公式(3)所示:
| $ {\overline y _D} = \int\limits_0^\infty {{\rm{ }}y{\rm{d}}\left( y \right){\rm{d}}y} {\rm{ }} = {\rm{ }}\frac{{\int_0^\infty {{y^2}f\left( y \right){\rm{d}}y} }}{{\int_0^{^\infty } {yf\left( y \right){\rm{d}}y} }}{\rm{ }} = {\rm{ }}\frac{{\int_{_0}^{^\infty } {{y^2}f\left( y \right){\rm{d}}y} }}{{yF}} $ | (3) |
由于线能是针对单次能量沉积事件定义的,微剂量学提供单粒子能谱,将物质中电离辐射的吸收与生物目标(例如单个细胞)的大小联系起来。
2、微剂量谱处理方法微剂量谱在早期文献中也称为线能谱,通常用线能y的剂量分布表示微剂量分布。由于测到的微剂量谱的线能分布范围较宽,往往跨越几个数量级,故在双线性坐标下往往不利于线能分布的表达,因此选择合适的图形表示方法非常重要。微剂量学中常见的微剂量谱一般是在对数-线性坐标下作图,这样可以体现yd(y)与log(y)的比值,yd(y)表示线能为y到y+dy之间的吸收剂量占总吸收剂量的分数,yd(y) 表示线能y的吸收剂量。坐标转换过程当中需要进行归一条件的对应转换,归一条件如公式(4)所示:
| $ \int\limits_{{y_1}}^{{y_2}} {{\rm{d}}y{\rm{d}}y} {\rm{ }} = \int_{{y_1}}^{^{{y_2}}} {[y{\rm{d}}(y)]{\rm{d}}({\rm{ln}}y)} {\rm{ }} = {\rm{ln}}\left( {10} \right)\int_{_{{y_1}}}^{{y_2}} {[y{\rm{d}}\left( y \right)]} {\rm{d}}({\rm{log}}y){\rm{ }} $ | (4) |
微剂量谱可以用来表征辐射场的微剂量分布,因此可以通过将微剂量学物理量与生物加权函数或微剂量动力学(microdosimetric kinetic model,MKM)模型相结合来获得RBE。
利用生物加权函数r(y)和线能y的剂量概率密度d(y),可以根据以下公式(5)估计RBE:
| $ {\rm{RBE}} = \int {r\left( {y} \right){\rm{d}}\left( {y} \right){\rm{d}}y} $ | (5) |
MKM模型最初由Hawkins[20]引入,然后由Kase等[21]逐步修改建立。其生物有效RBE是以人类唾液腺(human salivary gland,HSG)细胞体外培养10%细胞存活率为生物学终点,通常记为RBE10。根据细胞存活的线性平方模型(linear quadratic model,LQ模型),细胞存活分数S表达式为:
| $ S = {e^{ - \alpha D - \beta {D^2}}} $ | (6) |
对于MKM模型,α可以表示为:
| $ \alpha = {\alpha _0} + \frac{\beta }{{\rho {\rm{ \mathsf{ π} }}{r^2}_d}}{y^*} $ | (7) |
式中,αo为存活分数曲线在极限为零时的初始斜率,0.13 Gy-1;β为辐射独立参数,取0.05 Gy-2;ρ为组织的假定密度;rd=0.42 μm代表MKM模型中亚细胞区域半径;饱和校正剂量平均线能y*可以通过实验测得的微剂量谱确定为:
| $ {y^*} = {\rm{ }}\frac{{y_0^2\int_{_0}^\infty {(1 - \mathop e\nolimits^{ - \frac{{{y^2}}}{{y_0^2}}} )} f\left( y \right){\rm{d}}y}}{{{y_F}}} $ | (8) |
式中,y0为饱和度参数,150 keV/μm,用于修正高传能线密度(linear energy transfer,LET)辐射的过杀伤效应。然后根据LQ模型,利用如下关系式计算RBE:
| $ {\rm{RBE}} = \frac{{{D_R}}}{D} = \frac{{2\beta {D_R}}}{{\sqrt {{\alpha ^2} - 4\beta {\rm{ln}}\left( S \right)} {\rm{ }} - \alpha }} $ | (9) |
式中,D为细胞存活分数为S下的碳离子剂量,Gy;D′ R为相同细胞存活分数下的参考辐射剂量,Gy。
4、实验设备与仪器本实验测量使用的SOI硅微剂量计测量装置是由澳大利亚卧龙岗大学放射医学物理中心(CMRP)研发[12],微剂量测量装置主要由几部分组成:SOI硅微剂量计与前置放大器集成电路,探测器裸片尺寸为4.1 mm×3.6 mm,由在10 μm厚的n型绝缘体上硅衬底的4 248个硅阵列组成,用于模仿生物细胞;用于测量系统的成形放大器、偏压供应箱以及SOI硅微剂量计的PMMA护套,同时为防止电磁干扰,外层用铝箔纸进行包裹。当入射粒子与探测器转换层材料相互作用后有可能直接或间接地产生电子等次级粒子,这些次级带电粒子经过探测器灵敏区域时,发生电离而产生电荷被强电场收集,同时在PIN两极产生感应电荷,从而输出脉冲信号。
兰州重离子加速器国家实验室提供本次实验使用的散射束流,方向为垂直照射,碳离子束流为能量260 MeV/u的12C离子束,束流强度为1×108个粒子/脉冲,射野大小10 cm×10 cm,足够覆盖探测器。
5、测量方法在探测器上方,通过摆放不同厚度PMMA的组合,实现不同等效水深度的测量。本次实验以SOI硅微剂量计探测器表面为测量零点,PMMA板最小厚度是0.1 mm,从而实现了峰区位置更好的测量空间分辨率。实验根据测量得到的剂量平均线能与深度曲线,在曲线的坪区(45.5~113.5 mm)、布拉格峰区(116.1~117.0 mm)、峰尾(117.5~125.5 mm)等不同PMMA深度处,共得到23个测点信息及其微剂量谱。由于测量结果显示布拉格峰在116.5 mm位置处,为了更精细地描述布拉格峰附近微剂量谱的变化趋势,故在PMMA深度为116.1~117.0 mm处设置测量步长为0.1 mm。SOI硅微剂量计的成形放大器提供了低、中、高3档放大倍数(分别为10、100、1 000),对于12C离子束,选择使用低档放大倍数。为保证总计数要求,每个点照射时间为300 s。每测完一个点,更换PMMA片。
实验测量如图 1所示,12C离子束流从上而下垂直照射,束流射野中心穿过探测器灵敏体积中心。
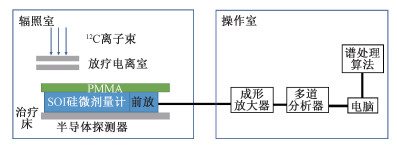
|
图 1 SOI硅微剂量计测量12C离子束流示意图 Figure 1 Schematic diagram of carbon ion beam measured by SOI silicon microdosimeter |
本研究将实验直接测量得到物理量导出,通过引入微剂量学相关物理量算法及RBE等算法进行计算,包括:剂量平均线能yD、概率平均线能yF、RBE10,以及yf(y)对y的分布、yd(y)对y的分布、yD的深度分布和RBE10的深度分布。由SOI硅微剂量计内部结构可知[22],灵敏体积为中间层的SiO2,从粒子到达SOI微剂量探测器表面至灵敏体积,中间经过10 μm厚Si、1.43 μm厚SiO2及1.7 μm的Al等材料,由于都非常薄,对12C离子束流影响小,可忽略不计。SOI硅微剂量计的PMMA保护套入射窗有0.5 mm厚PMMA,不可忽略,因此测量的固有等效PMMA深度为0.5 mm。
结果 1、剂量平均线能深度分布图 2为260 MeV/u的12C离子束的剂量平均线能yD与PMMA深度关系图。由图 2可以看出,该12C离子束的剂量线能值在PMMA中峰位为116.5 mm,等效水深度为134.2 mm,最大峰值可达97.0 keV/μm。同时,根据蒙特卡罗程序Geant4模拟得到水中不同深度处的剂量,得到的峰位为135.2 mm[22],峰位深度略高于实验测量深度,这是由于12C离子束在照射PMMA前会经过平板电离室等设备,会有一定程度的衰减,因此,会出现模拟值的峰位略高于实验测量值的情况。实验测量得到的峰宽在峰前上升沿约为3.0 mm,峰后下降沿约为2.0 mm。同时,在坪区入口处的剂量平均线能值与尾部的剂量平均线能值之比约为1 ∶2,也就是说,拖尾处剂量为坪区入口处的2倍左右,此部分主要来自于重离子作用产生的反冲质子等次级粒子具有较高线能的贡献,由此可见,12C离子束尾部的剂量不可忽略。
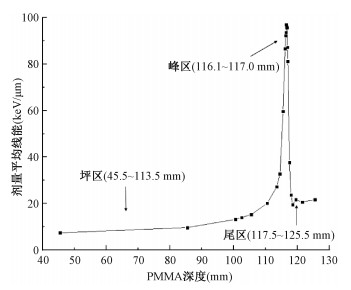
|
图 2 深度-剂量平均线能yD测量曲线 Figure 2 Measured curve of depth-dose mean line energy yD |
2、不同深度处的微剂量谱
本实验测量得到260 MeV/u的12C离子束在PMMA不同深度处的微剂量谱,因条件限制仅测量了单能的束流情况。与文献中测量所得结果对比[5],不同深度处微剂量谱变化趋势一致。图 3A为坪区处所测得微剂量谱,在坪区深度,即PMMA深度45.5~113.5 mm,随着深度增加,微剂量谱峰位逐渐向高线能区移动,同时峰值逐渐下降,全峰逐渐展宽。峰位由6.3 keV/μm逐渐向高线能区移动,直至25.12 keV/μm;峰值由0.33逐渐降至0.07,同时随着深度增加,峰慢慢出现展宽。
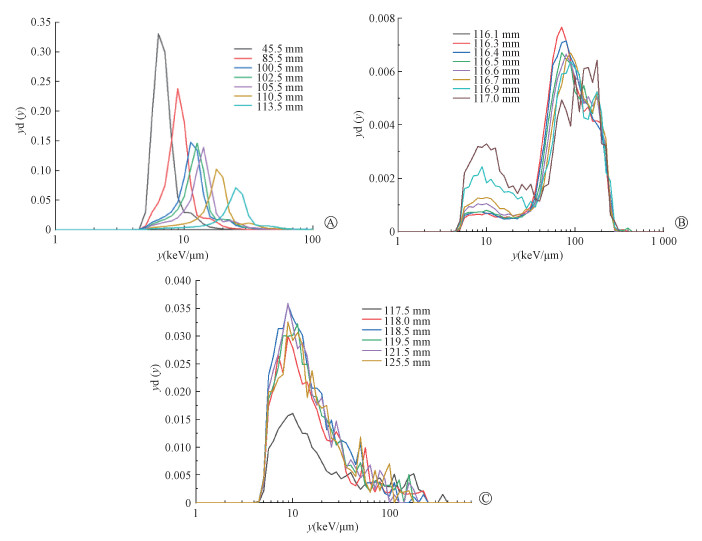
|
图 3 不同PMMA深度处微剂量谱A.坪区(45.5~113.5 mm);B.峰区(116.1~117.0 mm);C. 峰尾(117.5~125.5 mm) Figure 3 Microdosimetric spectra at different PMMA depths A. Flat region (45.5-113.5 mm); B. Bragg Peak (116.1-117.0 mm); C. Tail (117.5-125.5 mm) |
图 3B为峰值区间,即116.1~117.0 mm PMMA深度处的微剂量谱。此处测量深度间隔为0.1 mm。可以看到,谱线前沿有较低平台,峰的形状不规则,下降沿缓平,谱所在线能区间基本不变,随着深度增加,峰位略微向高线能区移动,同时低线能所占比例逐渐升高。在峰值处,即116.5 mm附近PMMA深度处260 MeV/u的12C离子束微剂量谱微剂量可见,谱峰位为70.79 keV/μm,在上升沿处迅速增加至yd(y)值为6.47×10-3。随后随着线能增加,yd(y)值缓慢减小,直至线能增加值2.82×102 keV/μm时,yd(y)值减少至4×10-5量级,可忽略不计。
图 3C为峰尾处,即PMMA深度由117.5~125.5 mm处的微剂量谱。随着深度增加,微剂量谱峰位逐渐向低线能区移动,峰值逐渐增加。在深度为125.5 mm时,移动至8.91 keV/μm处。峰尾位置处的微剂量谱测量结果与文献中用TEPC探测器测量得194 MeV/u的12C离子束峰尾位置处的微剂量谱趋势一致[5]。可以看出,在峰尾位置处吸收剂量的主要贡献来源于碳离子相互作用产生的次级粒子所造成的。yd(y)值起点线能区域不同,同样是由于两种不同探测器在后续数据处理过程中,截断设置的不同所导致的。
3、RBE深度分布图 4为260 MeV/u的12C离子束的RBE值与PMMA深度关系图,RBE值均由不同深度处所得微剂量谱结合MKM模型计算所得。由图 4可以看出,12C离子束的RBE值在PMMA中峰位为116.5 mm,可推算出等效水深度为134.2 mm,RBE值峰位与其剂量线能峰值一致。12C离子束的RBE值在峰前陡然上升,最大可以达到2.6,峰前上升沿处峰宽大概为3.0 mm;12C离子束RBE值在峰后迅速下降,在118.5 mm处低至1.2,下降沿大概为2.0 mm,拖尾为7.0 mm。此外,12C离子束RBE值拖尾处约为1.3,较坪区入口处1.0高出30%,此部分主要来自于重离子作用产生的反冲质子等具有较高线能的次级粒子造成的贡献,因此12C离子束在拖尾处的生物学效应不可忽略。

|
注:PMMA.聚甲基丙烯酸甲酯;RBE.相对生物学效应 图 4 PMMA深度与RBE10关系曲线 Figure 4 Relationship between PMMA depth and RBE10 |
讨论
重离子治疗的主要优点之一是提高了靶区离子束的RBE,高RBE是由于核尺度上局部电离密度增加所致[2]。因此,在重离子治疗中,正确确定重离子的RBE值不可或缺,微剂量谱是常用RBE计算模型中的关键环节,SOI硅微剂量计具有灵敏体积小、可以与其他类型探测器耦合、无需气体系统、无需高压(工作电压仅需10 V)、极高的空间分辨率、噪声低等特点,在进行碳离子束微剂量谱测量中有一定的优势[11]。本文使用SOI硅微剂量计,首次对兰州重离子加速器国家实验室能量为260 MeV/u的12C离子束流进行了微剂量谱测量,在布拉格峰值区测量的空间分辨率为0.1 mm。实验测量所得的脉冲幅度谱经转化得到频率分布及剂量分布,从而得到了不同PMMA深度下260 MeV/u的12C离子束微剂量谱,以及剂量线能yD与RBE随不同等效水深度的变化关系。
测量结果表明,随着PMMA深度的增加,微剂量谱会逐渐向高线能区域移动,同时峰值逐渐减小,峰将逐渐展宽,测量得到的微剂量谱变化趋势与Gerlach等[5]使用组织等效正比电离室以0.25 mm为步长进行测量得到的微剂量谱一致。在峰区PMMA深度以0.1 mm为步长进行测量,得到了更详细的峰区微剂量谱形状。在峰区时随着深度增加,yd(y)值变化趋势一致,且在低线能部分有较小鼓包,这是由于布拉格峰位置处,碳离子相互作用产生的次级粒子造成的贡献。关于次级粒子,Haettner等[23]认为此部分剂量的主要贡献来自次级碎片(特别是质子和中子),这些碎片沿着初级粒子的穿透路径连续产生。yd(y)值起点区域线能数值与文献[24]略有区别,是因为探测器在后续数据处理过程中截断设置不同有关; 在峰区后,微剂量谱会逐渐向低线能区域移动,峰值逐渐增加,峰宽变小。平均剂量线能yD值在PMMA深度为116.5 mm(等效水深度为134.2 mm)处达到峰值,最大峰值可达97.0 keV/μm,剂量线能yD值在峰位后迅速下降,但在拖尾处仍会存在坪区入口处两倍的剂量平均线能。测量发现RBE10值在峰区最高可达2.6,拖尾处的RBE10值仍有1.3左右,Chartier等[11]使用SOI硅微剂量计对日本HIMAC加速器的290 MeV/u的12C离子束流测量所得到RBE10峰值结果为2.66,因此对于碳离子束的RBE计算非常重要,碳离子束在拖尾处的生物学效应不可忽略。
本研究为碳离子束微剂量谱提供基础数据,随着PMMA深度增加,12C离子束的RBE值逐渐上升并达到峰值,布拉格峰位后迅速下降但在拖尾处的生物学效应不可忽略,因此,对于12C离子束的RBE计算非常重要。同时体现不同线能区间处的导致的剂量份额,为评估重离子治疗中继发癌症的风险提供参考。
利益冲突 本文由署名作者按以下贡献声明独立开展不涉及各相关方的利益冲突
志谢 感谢中国科学院近代物理研究所、中国科学院重离子束辐射生物医学重点实验室的戴中颖、张晖、申国盛、李强等对本研究的大力支持与帮助
作者贡献声明 杨璟喆负责实验组织与测量、数据整理与分析、论文撰写与修改;李君利负责设计实验并对文章的知识性内容作批评性审阅;邱睿负责资料分析及设备支持;衣宏昌负责采集数据与设备调试指导;武祯负责组织协调
| [1] |
Elssser ST, Schulz-Ertner D. Heavy-ion tumor therapy: Physical and radiobiological benefits[J]. Rev Mod Phys, 2010, 82(1): 383-425. DOI:10.1103/RevModPhys.82.383 |
| [2] |
Da IT, Qiang LI, Chen W, et al. Dependence of relative biological effectiveness on dose in hypofractionated carbon ion beam radiotherapy[J]. Nucl Phys Rev, 2017, 34(4): 784-789. |
| [3] |
Burigo L, Pshenichnov I, Mishustin I, et al. Microdosimetry spectra and RBE of 1H, 4He, 7Li and 12C nuclei in water studied with Geant4[J]. Nucl Instruments Methods Phys Res, 2014, 320(1): 89-99. DOI:10.1016/j.nimb.2013.10.018 |
| [4] |
Wambersie A, Zoetelief J, Menzel HG, et al. The ICRU (International Commission on Radiation Units and Measurements): its contribution to dosimetry in diagnostic and interventional radiology[J]. Radiat Prot Dosim, 2005, 117(1-3): 7-12. DOI:10.1093/rpd/nci701 |
| [5] |
Gerlach R, Roos H, Kellerer AM. Heavy ion RBE and microdosimetric spectra[J]. Radiat Prot Dosimetry, 2002, 99(1-4): 413-418. DOI:10.1093/oxfordjournals.rpd.a006821 |
| [6] |
Lindborg L, Kyllonen JE, Beck P, et al. The use of TEPC for reference dosimetry[J]. Radiat Prot Dosimetry, 1999, 86(4): 285-288. DOI:10.1093/oxfordjournals.rpd.a032959 |
| [7] |
张伟华, 王志强. 组织等效正比计数器的测量原理和方法[J]. 核标准计量与质量, 2008, 22(3): 45-54. Zhang WH, Wang ZQ. Measurement principle and method of tissue equivalent proportional counter[J]. Nucl Stand Qual, 2008, 22(3): 45-54. DOI:10.3969/j.issn.1673-453X.2008.03.008 |
| [8] |
Conte V, Colautti P, Chiriotti S, et al. Mini-TEPC microdosimetric study of carbon ion therapeutic beams at CNAO[J]. Eur Phys J Con, 2017, 153(9): 01012. DOI:10.1051/epjconf/201715301012 |
| [9] |
李春娟, 张伟华, 肖雪夫, 等. GEM-TEPC调研分析及原理研究[J]. 宇航计测技术, 2019, 39(1): 22-26. Li CJ, Zhang WH, Xiao XF, et al. GEM-TEPC investigation and analysis and principle research[J]. Astro Mea Technol, 2019, 39(1): 22-26. |
| [10] |
雷鸣, 刘书焕, 宗鹏飞, 等. SOI硅微剂量探测器对中子和伽马辐射场线能谱测量的GEANT4模拟研究[J]. 辐射防护, 2017, 37(3): 169-173. Lei M, Liu SH, Zong PF, et al. Geant4 simulation study on measurement of neutron and gamma radiation field line energy spectrum by SOI silicon microdose detector[J]. Radiat Prot, 2017, 37(3): 169-173. |
| [11] |
Chartier L, Tran LT, Bolst D, et al. Microdosimetric applications in proton and heavy ion therapy using silicon microdosimeters[J]. Radiat Prot Dosimetry, 2018, 180(1-4): 365-371. DOI:10.1016/j.radmeas.2018.06.015 |
| [12] |
Tran LT, Chartier L, Bolst D, et al. Characterization of proton pencil beam scanning and passive beam using a high spatial resolution solid-state microdosimeter[J]. Med Phys, 2017, 44(11): 6085-6095. DOI:10.1002/mp.12563 |
| [13] |
Wieser HP, Cisternas E, Wahl N, et al. Development of the open-source dose calculation and optimization toolkit matRad[J]. Med Phys, 2017, 44(6): 2556-2568. DOI:10.1002/mp.12251 |
| [14] |
Polster L, Schuemann J, Rinaldi I, et al. Extension of TOPAS for the simulation of proton radiation effects considering molecular and cellular endpoints[J]. Phys Med Biol, 2015, 60(13): 5053-5070. DOI:10.1088/0031-9155/60/13/5053 |
| [15] |
Wroe A, Rosenfeld A, Schulte R. Out-of-field dose equivalents delivered by proton therapy of prostate cancer[J]. Med Phys, 2007, 34(9): 3449-3456. DOI:10.1118/1.2759839 |
| [16] |
Borak TB, Doke T, Fuse T, et al. Comparisons of LET distributions for protons with energies between 50 and 200 MeV determined using a spherical tissue-equivalent proportional counter (TEPC) and a position-sensitive silicon spectrometer (RRMD-III)[J]. Radiat Res, 2004, 162(6): 687-692. DOI:10.1667/rr3262 |
| [17] |
Tsuda S, Sato T, Takahashi F, et al. Measurement of microdosimetric spectra with a wall-less tissue-equivalent proportional counter for a 290 MeV/u 12C beam[J]. Phys Med Biol, 2010, 55(17): 5089-5101. DOI:10.1088/0031-9155/55/17/013 |
| [18] |
Pan CY, Huang YW, Cheng KH, et al. Microdosimetry spectra and relative biological effectiveness of 15 and 30 MeV proton beams[J]. Appl Radiat Isot, 2015, 97: 101-105. DOI:10.1016/j.apradiso.2014.12.019 |
| [19] |
Dewey S, Burigo L, Pshenichnov I, et al. Lateral variations of radiobiological properties of therapeutic fields of 1H, 4He, 12C and 16O ions studied with Geant4 and microdosimetric kinetic model[J]. Phys Med Biol, 2017, 62(14): 5884-5907. DOI:10.1088/1361-6560/aa75b2 |
| [20] |
Hawkins RB. A microdosimetric-kinetic model for the effect of non-Poisson distribution of lethal lesions on the variation of RBE with LET[J]. Radiat Res, 2003, 160(1): 61-69. DOI:10.1667/rr3010 |
| [21] |
Kase Y, Kanai T, Matsufuji N, et al. Biophysical calculation of cell survival probabilities using amorphous track structure models for heavy-ion irradiation[J]. Phys Med Biol, 2008, 53(1): 37-59. DOI:10.1088/0031-9155/53/1/003 |
| [22] |
Zhu H, Chen Y, Sung W, et al. The microdosimetric extension in TOPAS: development and comparison with published data[J]. Phys Med Biol, 2019, 64(14): 145004. DOI:10.1088/1361-6560/ab23a3 |
| [23] |
Haettner E, Iwase H, Schardt D. Experimental fragmentation studies with 12C therapy beams[J]. Radiat Prot Dosim, 2006, 122(1-4): 485. DOI:10.1093/rpd/ncl402 |
| [24] |
Martino G, Durante M, Schardt D. Microdosimetry measurements characterizing the radiation fields of 300 MeV/u 12C and 185 MeV/u 7Li pencil beams stopping in water[J]. Phys Med Biol, 2010, 55(12): 3441-3449. DOI:10.1088/0031-9155/55/12/011 |
 2021, Vol. 41
2021, Vol. 41


