中华放射医学与防护杂志  2020, Vol. 40 Issue (9): 679-684   PDF    
引用本文
周解平, 彭昭, 王鹏, 常艳奎, 盛六四, 吴爱东, 钱立庭, 裴曦. 基于深度学习的直肠癌术后调强放疗剂量分布预测[J]. 中华放射医学与防护杂志, 2020, 40(9): 679-684, DOI: 10.3760/cma.j.issn.0254-5098.2020.09.005.
基于深度学习的直肠癌术后调强放疗剂量分布预测
周解平1 , 彭昭2 , 王鹏1 , 常艳奎2 , 盛六四3 , 吴爱东1 , 钱立庭1 , 裴曦2     
1. 中国科学技术大学附属第一医院 安徽省立医院 放疗科, 合肥 230031;
2. 中国科学技术大学物理学院工程应用物理系, 合肥 230026;
3. 中国科学技术大学国家同步辐射实验室, 合肥 230029
收稿日期: 2020-03-05
基金项目: 安徽省自然科学基金(1908085MA27)；安徽省重点研究与开发计划(1804a09020039)
通信作者: 裴曦, Email:xpei@ustc.edu.cn
[摘要] 目的 建立一种深度学习模型预测调强放疗(IMRT)的三维剂量分布。方法 收集直肠癌术后IMRT患者共110例，随机数表法选择其中90例作为训练验证集并作9折交叉验证，剩下20例作为测试集。构建3D U-Res-Net模型，以CT影像、靶区和危及器官(OARs)的解剖结构以及射束信息作为输入，IMRT剂量作为输出训练该模型，并用来预测测试集病例的剂量分布。采用三维剂量分布以及剂量—体积直方图(DVH)剂量参数评估预测精确性。结果 在三维剂量分布上，体素剂量的平均预测偏差为-2.12%~2.88%、平均绝对误差为2.55%~5.75%；等剂量面的Dice系数均在0.9以上，平均霍夫距离(HD95)和平均表面距离(MSD)分别0.61~1.54 cm和0.21~0.45 cm。对于DVH剂量参数，除膀胱Dmean(P=0.048)以外，其他剂量学参数差异均无统计学意义(P>0.05)。结论 基于3D U-Res-Net模型可以实现直肠癌术后IMRT剂量分布预测，为自动计划设计奠定基础。
[关键词] 深度学习    剂量预测    直肠癌    调强放疗    
Dose distributions prediction for intensity-modulated radiotherapy of postoperative rectal cancer based on deep learning
Zhou Jieping1 , Peng Zhao2 , Wang Peng1 , Chang Yankui2 , Sheng Liusi3 , Wu Aidong1 , Qian Liting1 , Pei Xi2     
1. Department of Radiation Oncology, First Affiliated Hospital of USTC, Division of Life Sciences and Medicine, University of Science and Technology of China, Hefei 230031, China;
2. Department of Engineering and Applied Physics, School of Physics, University of Science and Technology of China, Hefei 230026, China;
3. National Synchrotron Radiation Laboratory, University of Science and Technology of China, Hefei 230029, China
Fund programs: General Program of Anhui Natural Science Foundation (1908085MA27); Anhui Key Research and Development Plan (1804a09020039)
Corresponding author: Pei Xi, Email:xpei@ustc.edu.cn
[Abstract] Objective To develop a deep learning model for predicting three-dimensional (3D) voxel-wise dose distributions for intensity-modulated radiotherapy (IMRT). Methods A total of 110 postoperative rectal cancer cases treated by IMRT were considered in the study, of which 90 cases were randomly selected as the training-validating set and the remaining as the testing set. A 3D deep learning model named 3D U-Res-Net was constructed to predict 3D dose distributions. Three types of 3D matrices from CT images, structure sets and beam configurations were fed into the independent input channel, respectively, and the 3D matrix of IMRT dose distributions was taken as the output to train the 3D model. The obtained 3D model was used to predict new 3D dose distributions. The predicted accuracy was evaluated in two aspects:the average dose prediction bias and mean absolute errors (MAEs)of all voxels within the body, the dice similarity coefficients (DSCs), Hausdorff distance(HD95) and mean surface distance (MSD) of different isodose surfaces were used to address the spatial correspondence between predicted and clinical delivered 3D dose distributions; the dosimetric index (DI) including homogeneity index, conformity index, V50, V45 for PTV and OARs between predicted and clinical truth were statistically analyzed with the paired-samples t test. Results For the 20 testing cases, the average prediction bias ranged from -2.12% to 2.88%, and the MAEs varied from 2.55% to 5.75%. The DSCs value was above 0.9 for all isodose surfaces, the average MSD ranged from 0.21 cm to 0.45 cm, and the average HD95 varied from 0.61 cm to 1.54 cm. There was no statistically significant difference for all DIs, except for bladder Dmean. Conclusions This study developed a deep learning model based on 3D U-Res-Net by considering beam configurations input and achieved an accurate 3D voxel-wise dose prediction for rectal cancer treated by IMRT.
[Key words] Deep learning    Dose prediction    Rectal cancer    IMRT    

调强放疗(intensity modulate radiotherapy, IMRT)计划设计者常常根据临床指南的危及器官(organs at risk, OARs)剂量限值设定优化函数，但临床指南通常是基于群体的平均数据，不能反映个性化剂量信息[1]。因此，计划设计者常常不断地尝试和修改优化函数以获得最优计划，但不同的治疗中心和计划设计者之间由于经验、技巧以及时间等差异设计出的治疗计划质量差别较大[2]，严重地影响患者治疗效果。因此，迫切地需要在IMRT计划设计前精准地预测个性化的剂量分布，提高治疗计划的质量和效率[3-4]。目前国内外多名学者进行了剂量预测的相关研究，其中最常见的是“基于经验的放疗”(knowledge based radiotherapy, KBRT) [5-6]，但该方法需要手动方式提取几何特征且不能预测三维剂量分布。因此，本研究建立一种基于3D U-Net[7]和残差网络[8]的三维深度学习模型3D U-Res-Net，该模型自动地学习三维的CT影像、结构组及射束中多尺度、多层次特征实现精确的三维剂量分布预测。

资料与方法

1.直肠癌IMRT数据库及数据处理：收集2015—2018年直肠癌术后IMRT治疗的患者共110例，其中T2N+ 36例、T3 54例和T4 20例，盆腔磁共振提示均无阳性淋巴结，随机数表法选取其中20例作为测试集，剩下90例按8:1比例分成训练集和验证集并作九折交叉验证。所用患者靶区处方剂量均为95%计划靶区体积(PTV) 50 Gy/25次，采用Pinnacle计划系统，6 MV X射线共面5~7野设计IMRT计划，该计划所有剂量参数均满足临床标准[9]，且三维剂量分布均经过主任物理师的审核。使用自主开发的Python程序转换IMRT计划的CT影像、结构组、三维剂量分布及射束信息成各自的三维矩阵。CT影像的三维矩阵：首先将CT值截取至-200~300 HU(Hounsfield unit)，然后归一化至-1~1。结构组的三维矩阵：分别采用不同的数字标签标记靶区PTV和各OAR的体素，并归一至0~1。IMRT剂量的三维矩阵归一至0~1。射束的三维矩阵采用三维适形放疗剂量表征：其中各射束权重比例相同、数量和方向与该IMRT计划相同、适形为PTV在射野方向视图(beam eye view, BEV)投影并均匀外扩5 mm，卷积叠加算法计算最终三维全空间剂量。重采样所有三维矩阵至2.5 mm×2.5 mm×2.5 mm的分辨率，并裁剪成128×128×128的大小。

2. 3D U-Res-Net模型及训练：本研究采用以TensorFlow为后端的Python深度学习库Keras构建一个基于3D U-Net和残差网络(residual net)的三维深度学习模型—3D U-Res-Net[10]。该网络由编码器和解码器两部分组成。编码器由5个编码模块组成，每个模块又由不同数量的Res_block组成，Res_block均含有4个卷积层，其卷积核的大小分别为1×1×1、3×3×3、1×1×1、3×3×3；此外编码器的前4个模块末端还采用大小为3×3×3、步长为2×2×2的卷积操作进行下采样；所有卷积层后均采用批量归一化(batch normalization, BN)和修正线性单元(rectified linear unit, ReLU)操作。解码器含有5个解码模块；其中第1个模块仅包含1个3×3×3的卷积层，其余4个模块均包含1个Conv_block，而Conv_block由3个卷积层组成，其卷积核的大小分别为1×1×1、3×3×3和3×3×3；前4个模块末端还采用大小为3×3×3、步长为2×2×2的反卷积进行上采样；所有(反)卷积层后均执行ReLU操作。最后，使用3×3×3的卷积和ReLU操作预测最终剂量。

CT影像、结构组和射束3类三维矩阵采用平移、旋转及翻转等数据扩增方式以128×128×128×3形式作为输入，IMRT剂量三维矩阵以128×128×128×1形式作为输出；预测剂量与原临床剂量均方差作为损失函数，采用Adam优化算法训练3D U-Res-Net模型，并用最优模型预测测试集病例的剂量分布。

3.剂量预测精确性的评估

(1) 三维剂量分布比较：首先计算体素剂量的平均预测偏差$ \overline {\delta D} $及平均绝对误差(mean absolute errors, MAE)，计算公式如下：

$ \overline {\delta D} = \frac{1}{n}\sum\limits_i^n {\left( {{D_{\rm{c}}} - {D_{\rm{p}}}} \right)} $ (1)
$ {\rm{MAE}} = \frac{1}{n}\sum\limits_i^n {\left| {{D_{\rm{c}}} - {D_{\rm{p}}}} \right|} $ (2)

式中，Dc和Dp分别为体素剂量的临床和预测值；i为某体素点；n为体内所有体素点。

其次，采用Dice系数(dice similarity coefficients, DSC)、霍夫距离(Hausdorff distance，HD95)及平均表面距离(mean surface distance, MSD)预测和分析临床的等剂量面的相似性程度[11]。Dice系数计算的剂量范围为1~50 Gy，间隔为1 Gy；HD95/MSD计算的剂量范围为20~50 Gy，间隔为5 Gy。

(2) DVH剂量学参数比较：比较预测和临床的PTV和OARs的剂量学参数，包括PTV的平均剂量(Dmean)、D2、D50、D98(Di为i%的PTV体积接受的剂量)、适形度指数(CI)[12]和均匀性指数(HI)[13]，OARs的Dmean、V45、V50(Vi为接受i Gy剂量的OARs体积百分比)。

4.统计学处理：采用SPSS 22.0软件进行统计学处理，数据符合正态分布，结果采用x±s表示，对交叉验证组合1与其他组合及原临床计划进行配对t检验。P < 0.05为差异有统计学意义。

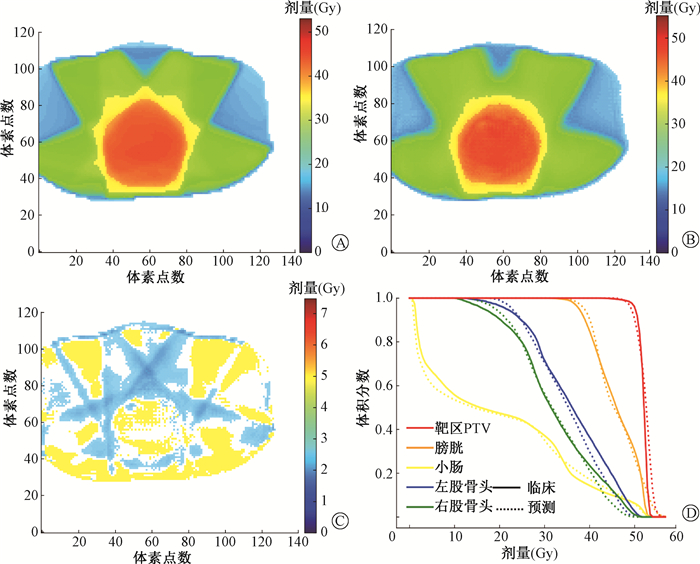
结果

1.三维剂量分布比较：随机选取1例测试集病例，原临床剂量分布、相应的预测剂量分布和体素级剂量分布差异示于图 1。结果显示，在各个剂量水平上预测的与原临床的剂量分布基本相似，体素的剂量差异均在5 Gy以下，且两者靶区PTV和OARs的DVH曲线均较为一致。

A.原临床剂量分布；B.预测的剂量分布；C.剂量分布差异；D.总DVH图 图 1 随机选择1例测试集病例三维剂量分布及DVH比较 A.Clinical dose distributions; B.Predicted dose distributions; C.Dose difference map; D. The overall DVH curve Figure 1 Dose distributions comparison between prediction and clinical truth for a randomly selected testing case

20例测试集病例体素剂量的平均预测偏差 $ \overline {\delta D} $ 为-2.12%~2.88%，平均MAE为2.55%~5.75%；各等剂量的Dice系数均在0.9以上，平均Dice系数在0.92以上，平均HD95和MSD分别为0.61~1.54 cm和0.21~0.45 cm(图 2)。

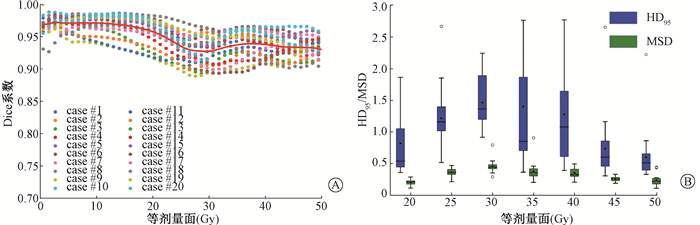
注：HD.霍夫距离；MSD.平均表面距离 图 2 20例测试集病例预测与原临床等剂量面的相似性A. Dice系数(红实线表示平均值)；B.HD95/MSD(黑点表示平均值) Figure 2 The similarity of isodose surfaces between prediction and clinical truth for the 20 testing cases A. Dice similarity coefficients; B. Hausdorff distance 95% and mean surface distance

2. DVH剂量学参数比较：PTV的D2、D50、D98、Dmean和OARs的Dmean预测的平均绝对误差在2%以内，OARs的V50、V45预测的平均绝对误差小于5%，除膀胱Dmean (P=0.048)外，其他剂量学参数差异均无统计学意义，详见表 1。

表 1 20例测试集病例原临床和预测的剂量学参数比较(x±s) Table 1 Comparison of the dosimetric parameters between prediction and clinical truth for the 20 testing cases (x±s)

3.交叉验证组在测试集上的结果：9折交叉验证的剂量预测结果示于表 2，上述结果为交叉验证组合1的预测结果，与其他交叉验证组的差异无统计学意义(P>0.05)。

表 2 9折交叉验证的平均剂量预测偏差和绝对误差(%, x±s) Table 2 The average prediction bias and absolute errors in the testing set for 9-fold cross-validation model(%, x±s)

讨论

本研究建立了3D U-Res-Net深度学习模型自动地学习CT影像、结构组及射束中多尺度、多层次特征实现直肠癌IMRT剂量分布预测。由于该模型直接采用靶区和OARs结构组及射束等的三维矩阵作为输入，而剂量分布与三维的解剖结构及射束等紧密相关[14-16]。因此，理论上本研究模型可能比其他二维深度学习模型自动提取更多的特征，实现更精确的剂量预测。此外，虽然本研究模型实现了直肠癌IMRT剂量预测，但对其他的肿瘤部位及调强技术同样适用，如鼻咽癌的旋转调强放疗等。

基于3D U-Res-Net模型的20例测试集病例预测结果显示，总的平均预测偏差为(0.02±4.82)%，总的平均绝对误差为(4.03±4.32)%；所有等剂量面的Dice系数均在0.90以上，特别是20 Gy以下的Dice系数达到0.95以上；除膀胱Dmean以外，其他所有的DVH剂量参数差异均无统计学意义, 这些结果均表明基于3D U-Res-Net模型的剂量预测是足够精确的。然而，由于肿瘤靶区和OARs的勾画及靶区的处方剂量和OARs的剂量限制等差异，本模型的预测结果可能仅适用于本肿瘤放疗中心，对于其他的治疗中心，应基于该中心的优质放疗计划数据库，利用本研究中的三维深度学习模型建立自己的预测模型。等剂量面的Dice系数从25 Gy到30 Gy时有所下降，与HD95/MSD结果一致，可能与提取的不完全射束特征等有关；在较高的等剂量面如48 Gy时，Dice系数也呈下降趋势，这可能与高剂量区等剂量面较小等有关。

Shiraishi和Moore[17]手动提取体素相对于PTV距离和角度的特征，基于人工神经网络(artificial neural network，ANN)预测前列腺VMAT和立体定向放疗的剂量分布，结果显示平均预测偏差分别为10%和8%。McIntosh和Purdie[18]应用atlas回归森林(atlas regression forests，ARF)预测乳腺切线野IMRT、乳腺腔非共面野IMRT、前列腺VMAT的剂量分布，结果显示平均Dice系数分别为0.86、0.76、0.86。与这些方法相比，本研究利用深度学习模型自动地提取特征，避免了复杂繁琐的特征提取任务且提取的特征更加全面，获得了更好的预测结果。

有研究者利用深度学习进行了剂量预测[19-22]。Nguyen等[19]使用分层紧密连接的U-Net实现前列腺癌IMRT的剂量预测，结果表明，器官Dmax和Dmean的平均预测偏差均在5.1%以下，等剂量面的平均Dice系数为0.91；Liu等[20]使用二维残差网络实现鼻咽癌Tomo的剂量预测，结果表明，OARs的Dmax和Dmean的平均绝对预测误差分别为4.2%和2.4%，体素剂量的平均预测偏差范围为-2.0%~2.3%。由于模型训练采用了不同部位肿瘤及调强放疗技术的病例数据，因此很难直接比较本研究模型与其他模型的优劣，然而从结果上看本研究模型的剂量预测精度是在相同的范围内。

精确预测的剂量可以用来实现相同射束条件下IMRT计划的质量控制和优化设计，提高治疗计划的质量和设计效率；临床医生可以据此调整靶区和OARs的剂量约束，实现患者个性化治疗；此外还可以基于精确预测的体素剂量实现体素级剂量优化，生成更优的放疗计划[23]。基于本研究基础，课题组下一步拟开展临床医生不同剂量偏好对剂量预测影响和放疗计划自动设计研究。

志谢 本研究获得中国科学技术大学附属第一医院西区青年基金(2018YJQN014)的资助

利益冲突  无

作者贡献声明  周解平负责论文撰写；常艳奎、彭昭负责深度学习模型构建；王鹏、裴曦负责数据的采集和处理；盛六四、吴爱东、钱立庭负责修改论文

参考文献
[1]
中国鼻咽癌临床分期工作委员会. 中国鼻咽癌分期2017版(2008鼻咽癌分期修订专家共识)[J]. 中华放射肿瘤学杂志, 2017, 26(10): 1119-1125.
Chinese Working Committee on Clinical Staging of Nasopharyngeal Carcinoma. The 2017 edition for staging of nasopharyngeal carcinoma in China (The Chinese 2008 expert consensus on staging revision of nasopharyngeal carcinoma)[J]. Chin J Radiat Oncol, 2017, 26(10): 1119-1125. DOI:10.3760/cma.j.issn.1004-4221.2017.10.002
[2]
Nelms BE, Robinson G, Markham J, et al. Variation in external beam treatment plan quality:an inter-institutional study of planners and planning systems[J]. Pract Radiat Oncol, 2012, 2(4): 296-305. DOI:10.1016/j.prro.2011.11.012
[3]
任信信, 戴建荣, 张岳, 等. 基于专家库的γ射线立体定向放疗计划优化方法[J]. 中国医学物理学杂志, 2015, 32(3): 301-305.
Ren XX, Dai JR, Zhang Y, et al. Planning optimization method based on expert database for γ ray stereotactic radiotherapy[J]. Chin J Med Phy, 2015, 32(3): 301-305. DOI:10.3969/j.issn.1005-202X.2015.03.001
[4]
Yuan L, Wu QJ, Yin FF, et al. Incorporating single-side sparing in models for predicting parotid dose sparing in head and neck IMRT[J]. Med Phys, 2014, 41(2): 021728. DOI:10.1118/1.4862075
[5]
贾启源, 郭芙彤, 吴艾茜, 等. 基于危及器官预测剂量分布与gEUD混合目标的调强放疗计划优化[J]. 中华放射医学与防护杂志, 2019, 39(6): 422-427.
Jia QY, Guo FT, Wu AX, et al. OAR predicted dose distribution and gEUD based treatment planning optimization for IMRT[J]. Chin J Radiol Med Prot, 2019, 39(6): 422-427. DOI:10.3760/cma.j.issn.0254-5098.2019.06.004
[6]
Li N, Carmona R, Sirak I, et al. Highly efficient training, refinement, and validation of a knowledge-based planning quality-control system for radiation therapy clinical trials[J]. Int J Radiat Oncol Biol Phys, 2017, 97(1): 164-172. DOI:10.1016/j.ijrobp.2016.10.005
[7]
Çiçek Ö, Abdulkadir A, Lienkamp SS, et al. 3D U-Net: learning dense volumetric segmentation from sparse annotation. In: medical image computing and computer-assisted intervention-MICCAI 2016[M]. Cham: Springer, 2016: 424-432.
[8]
Yu L, Chen H, Dou Q, et al. Automated melanoma recognition in dermoscopy images via very deep residual networks[J]. IEEE Trans Med Imaging, 2017, 36(4): 994-1004. DOI:10.1109/TMI.2016.2642839
[9]
中国医师协会结直肠肿瘤专委会放疗专委会, 唐源, 金晶, 等. 直肠癌术前/术后适形/调强放疗靶区勾画共识与图谱[J]. 中华放射肿瘤学杂志, 2018, 27(3): 227-234.
Professional Committee of Radiotherapy for Colorectal Cancer of Chinese Medical Doctor Association, Tang Y, Jin J, et al. Consensus and contouring atlas for the delineation of clinical target volume in pre-/post-operative image-guided intensity modulated radiotherapy for rectal cancer[J]. Chin J Radiat Oncol, 2018, 27(3): 227-234. DOI:10.3760/cma.j.issn.1004-4221.2018.03.001
[10]
Abadi M, Barham P, Chen JM, et al. Tensorflow: A system for large-scale machine learning[C]. Savannah: 12th USENIX Conference on Operating Systems Design and Implementation, 2016.
[11]
Wang B, Yang L, Tian SB, et al. Deeply supervised 3D fully convolutional networks with group dilated convolution for automatic MRI prostate segmentation[J]. Med Phys, 2019, 46(4): 1707-1718. DOI:10.1002/mp.13416
[12]
van't Riet A, Mak AC, Moerland MA, et al. A conformation number to quantify the degree of conformality in brachytherapy and external beam irradiation:application to the prostate[J]. Int J Radiat Oncol Biol Phys, 1997, 37(3): 731-736. DOI:10.1016/s0360-3016(96)00601-3
[13]
Hodapp N. The ICRU Report 83:prescribing, recording and reporting photon-beam intensity-modulated radiation therapy (IMRT)[J]. Strahlenther Onkol, 2012, 188(1): 97-99. DOI:10.1007/s00066-011-0015-x
[14]
Wu B, Ricchetti F, Sanguineti G, et al. Patient geometry-driven information retrieval for IMRT treatment plan quality control[J]. Med Phys, 2009, 36(12): 5497-5505. DOI:10.1118/1.3253464
[15]
Yuan L, Ge Y, Lee WR, et al. Quantitative analysis of the factors which affect the interpatient organ-at-risk dose sparing variation in IMRT plans[J]. Med Phys, 2012, 39(11): 6868-6878. DOI:10.1118/1.4757927
[16]
Potrebko PS, McCurdy BM, Butler JB, et al. A simple geometric algorithm to predict optimal starting gantry angles using equiangular-spaced beams for intensity modulated radiation therapy of prostate cancer[J]. Med Phys, 2007, 34(10): 3951-3961. DOI:10.1118/1.2775685
[17]
Shiraishi S, Moore KL. Knowledge-based prediction of three-dimensional dose distributions for external beam radiotherapy[J]. Med Phys, 2016, 43(1): 378. DOI:10.1118/1.4938583
[18]
McIntosh C, Purdie TG. Contextual atlas regression forests:Multiple-atlas-based automated dose prediction in radiation therapy[J]. IEEE Trans Med Imaging, 2016, 35(4): 1000-1012. DOI:10.1109/TMI.2015.2505188
[19]
Nguyen D, Long T, Jia X, et al. A feasibility study for predicting optimal radiation therapy dose distributions of prostate cancer patients from patient anatomy using deep learning[J]. Sci Rep, 2019, 9(1): 1076. DOI:10.1038/s41598-018-37741-x
[20]
Liu Z, Fan J, Li M, et al. A deep learning method for prediction of three-dimensional dose distribution of helical tomotherapy[J]. Med Phys, 2019, 46(5): 1972-1983. DOI:10.1002/mp.13490
[21]
Kearney V, Chan JW, Haaf S, et al. Dose Net:a volumetric dose prediction algorithm using 3D fully-convolutional neural networks[J]. Phys Med Biol, 2018, 63(23): 235022. DOI:10.1088/1361-6560/aaef74
[22]
Fan J, Wang J, Chen Z, et al. Automatic treatment planning based on three-dimensional dose distribution predicted from deep learning technique[J]. Med Phys, 2019, 46(1): 370-381. DOI:10.1002/mp.13271
[23]
Wieser HP, Cisternas E, Wahl N, et al. Development of the open-source dose calculation and optimization toolkit matRad[J]. Med Phys, 2017, 44(6): 2556-2568. DOI:10.1002/mp.12251