2. 安徽慧软科技有限公司, 合肥 230088;
3. 安徽省肿瘤医院放疗科, 合肥 230031;
4. 安徽大学计算机科学与技术学院, 合肥 230601;
5. 中国科学技术大学附属第一医院放疗科, 合肥 230031
2. Anhui Wisedom Technology Co. Ltd, Hefei 230088, China;
3. Department of Radiation Oncology, Anhui Provincial Cancer Hospital, Hefei 230031, China;
4. School of Computer Science and Engineering, Anhui University, Hefei 230601, China;
5. Deptartment of Radiotherapy, the First Affiliated Hospital of USTC, Hefei 230031, China
IMRT计划传统的优化方法是强度图优化(fluence map optimization,FMO),即先优化强度分布图,然后进行分群和子野分割得到子野信息。分割时要舍弃面积小、机器跳数(monitor unit,MU)少的子野,和实际强度的差别可达5.7%[1]。直接子野优化算法(direct aperture optimization,DAO)[2]将物理约束加入到优化过程中,直接对子野形状、权重等参数进行优化,不会出现子野分割前后强度不一致的问题。基于梯度的DAO算法在商用治疗计划系统(Pinnacle、RayStation等)中证明有良好的优化性能[3]。但是在DAO中,目标函数和叶片位置之间的关系是分段函数的形式,无法计算梯度。Cassioli等[3]在优化子野形状时用分段线性函数来近似梯度和目标函数,提出一种类似信赖域的算法,但只有在叶片变动小的情况下有效。杨婕等[4]在模拟退火和拟牛顿法中加入梯度信息,但优化时间较长。本研究在放疗计划系统DeepPlan中集成了一种基于共轭梯度法(conjugate gradient,CG)的快速DAO算法。算法用连续误差函数(erf函数)拟合强度分布,通过图形处理器(GPU)加速能在较短时间内得到高质量的放疗计划。
材料与方法1.模型建立:DeepPlan是中国科学技术大学放射医学物理中心与安徽慧软科技有限公司联合研发的放疗计划系统[5-8]。DeepPlan优化算法基于三维卷积叠加剂量计算模型[8],该模型已经通过《YY/T 0775-2010远距离放射治疗计划系统高能X(γ)射束剂量计算》报告[9]测试。优化算法编写基于CUDA 10.1和C++语言,采用TBB模型[10]、thrust并行算法库和cusp稀疏矩阵运算库[11]等,已经通过了《YY/T 0889-2013调强放射治疗计划系统性能和试验方法》报告[12]验证。优化算法在计算稀疏贡献矩阵和计算优化步长的梯度时数据量较大。针对稀疏贡献矩阵计算的加速,采用通量卷积宽束(fluence convolution broad beam,FCBB)算法[13]计算出只有主束贡献的稀疏剂量贡献矩阵,然后在优化过程中剂量校正部分可重用射线追踪结果,无需再计算。针对步长梯度计算的加速,除了使用并行算法库外,每次只计算多叶准直器(multi-leaf collimator,MLC)位置附近网格的梯度,避免了重复计算。本研究完成DeepPlan临床病例优化测试的计算机配置如下:操作系统为Windows 10(64位),CPU为Inter Core i7、6核12线程、32 G内存,GPU为GTX660(6 G)。
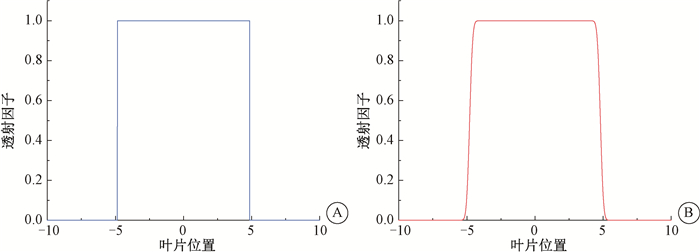
2.优化算法流程:首先,计算剂量贡献矩阵,根据计划靶区(planning tumor volume,PTV)和危及器官(organ at risks,OARs)的处方剂量,用共轭梯度法优化得到强度分布图[14]。然后,对每个射束进行强度分群和子野分割[15],得到初始子野形状和权重。如果子野数(segments number,SN)大于最大子野数,根据子野的品质因子[16]进行筛选。最后,交替优化子野形状和权重:固定权重不变,考虑叶片移动的物理限制,运用共轭梯度法优化子野形状;固定叶片位置不变,运用共轭梯度法优化子野权重[17],直到达到最大迭代次数或目标函数小于设定的阈值。DeepPlan的子野形状优化目标函数采用基于加权最小二乘法的剂量体积目标函数[14]。在子野形状优化中,MLC叶片只有开和闭(透射因子分别是1和0)两种离散状态,在开闭过渡处强度曲线无法求梯度,如图 1。而在实际治疗中,MLC叶片边缘会出现半影,强度曲线是连续下降的[18]。因此,DeepPlan采用erf函数[19]拟合子野的强度分布,不仅建立了叶片和强度之间的连续函数,同时减小MLC半影带来的误差。erf拟合曲线如图 1所示。
|
图 1 一对多叶准直器叶片开闭对应的强度曲线 A.阶梯分段的强度曲线;B. erf拟合的强度曲线 Figure 1 Intensity curve for a pair of multileaf collimator in closing and opening condition A. Intensity curve with staircase segmentation; B. Intensity curve fitted by erf function |
靶区或危及器官的第n个体素的剂量dotdosen见公式(1):
| $ {\rm{dotdos}}{{\rm{e}}_n} = \sum {_t{\rm{charmatri}}{{\rm{x}}_{n, t}}} \times \left( {\sum {_fm{u_{t, f}} \times {\rm{er}}{{\rm{f}}_{t, f}}} } \right) $ | (1) |
式中,charmatrixn, t是单位MU下第t个笔形束对第n个体素的剂量贡献;∑fmut, f×erft, f表示第t个笔形束在所有f个子野照射下的总跳数, erft, f函数见公式(2)。
| $ {\rm{er}}{{\rm{f}}_{t, f}} = \delta \times \left[ {{\rm{erf}}\left( {\frac{{{x_t} - {x_l}}}{\tau }} \right) - {\rm{erf}}\left( {\frac{{{x_t} - {x_r}}}{\tau }} \right)} \right] + T $ | (2) |
式中,xt、xl、xr分别是第f个子野中第t个笔形束的位置和所在行MLC的左、右叶片位置。δ代表归一化因子。τ是半影拟合参数,由机器实测参数决定。T代表叶片闭合时的透射率。结合式(1)和式(2)可求目标函数对叶片位置xl和xr的梯度。
3.评估方法:本研究分别从子野数(SN)、总机器跳数(MU)、均匀性指数(HI)和适形度指数(CI)4个方面对DeepPlan和Pinnacle系统的计划质量进行评估。在相同的剂量分布下,子野数越少,总的MU越小,计划质量越好[20]。HI是靶区的剂量均匀性指数,CI是处方剂量大小的适形度指数[21]。HI越接近于0则靶区剂量均匀性越好,CI越接近于1则靶区适形度越高。
4.测试数据:从安徽省肿瘤医院收集25例已行静态调强放疗的临床病例,其中包括6例头颈部、10例胸部和9例盆腔部。成像设备是美国GE公司Discovery CT 590,进行CT增强扫描,层厚为2.5 mm。由一名主治医生勾画出靶区和危及器官(OARs)并经主任医师审核确认。所有病例已经采用Pinnacle制定了静态调强放疗计划,治疗射束为加速器Trilogy 6 MV的X射线。本研究使用自主研发的DeepPlan计划系统对所有病例重新设计另一套静态调强放疗计划,并与原Pinnacle计划进行对比。每个病例中DeepPlan与Pinnacle计划具有相同的处方剂量约束、加速器参数、CT、器官勾画、剂量计算网格、最大子野数和射束信息。
5.统计学处理:采用SPSS 25.0软件进行统计学处理。PTV和OAR的剂量学参数、MU、子野数等用x±s表示,经检验相关数据符合正态分布。两系统之间的优化结果比较采用配对t检验。P < 0.05为差异有统计学意义。
结果1. DeepPlan优化结果:DeepPlan中25个病例优化时间和剂量计算时间列于表 1,DeepPlan的平均优化时间86 s,最小35 s,最大266 s,平均剂量计算时间8.36 s,最小2 s,最大23 s。DeepPlan中所有的靶区和危及器官剂量都满足临床要求。
|
|
表 1 使用DeepPlan的患者计划优化时间和剂量计算时间(s, x±s) Table 1 The optimization time and the dose calculation time of clinical cases in DeepPlan system(s, x±s) |
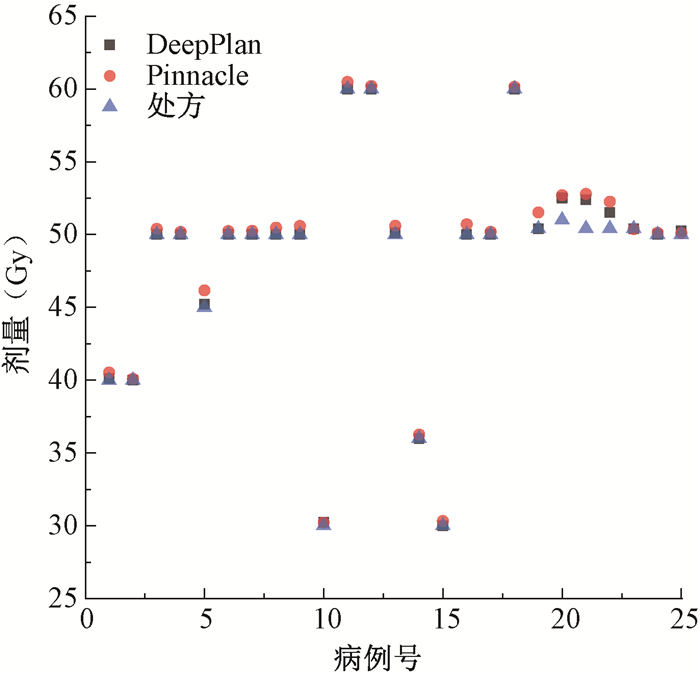
2. DeepPlan和Pinnacle优化结果对比:25例病例的靶区处方剂量(D95)与照射剂量(D95)对比如图 2,两系统中靶区D2、D50、D95、D98差异均无统计学意义(P>0.05)。相同射束条件下两系统的MU、SN、HI、CI结果对比列于表 2。
|
图 2 25例病例PTV的处方剂量(D95)与照射剂量(D95)剂量对比 Figure 2 Comparison between prescription dose and actual dose of PTV (D95) in 25 cases |
|
|
表 2 相同射束条件下25例患者DeepPlan与Pinnacle计划系统的剂量学参数比较(x±s) Table 2 Comparison of dosimetric parameters between DeepPlan and Pinnacle systems in the same beam condition for 25 cases (x±s) |
(1) 机器跳数对比:有6例病例的MUD大于MUP(下标“D”为此病例在DeepPlan的结果,下标“P”为在Pinnacle的结果,下同),最大差值为88;其余19例是MUD小于MUP,其中8例差值在100以上,最大差值为399。差异具有统计学意义(t=-3.208,P < 0.05)。
(2) 子野数对比:有8例病例的SND小于SNP,最大差值为6。有13例病例的SND大于SNP,其中7例差值在10以上,最大差值为27。差异具有统计学意义(t=2.912,P < 0.05)。
(3) CI、HI指数对比:有17例病例的CID>CIP,其中2例差值在0.2以上, 差异具有统计学意义(t=2.875,P < 0.05)。DeepPlan和Pinnacle的HI指数相似,差异无统计学意义(P>0.05)。
3.宫颈癌病例剂量学分析:由于25例病例中病种复杂,为便于说明,选取其中6例宫颈癌病例(病例4至病例9)进行剂量学参数展示。靶区和危及器官的部分剂量学参数比较列于表 3,其中Dx代表x%的体积对应的剂量(Gy),Vx代表x Gy的剂量对应的体积百分比(%)。与Pinnacle系统相比,DeepPlan对膀胱、左右股骨头的剂量体积约束稍好,对骨盆、直肠、小肠的剂量体积约束稍差,其中只有小肠的V20(t=2.581,P < 0.05)和膀胱的V40的差异具有统计学意义(t=-5.498,P < 0.05)。
|
|
表 3 相同射束条件下6例宫颈癌病例中DeepPlan与Pinnacle计划系统的剂量学参数比较(x±s) Table 3 Comparison of dosimetric parameters between DeepPlan and Pinnacle systems at the same beam for 6 cervical cancer cases (x±s) |
讨论
本研究中选取的宫颈癌剂量学参数具有临床意义:小肠V40是慢性胃肠道并发症的独立预测因子[22];骨盆V10、V20和白细胞、中性粒细胞计数下限显著相关[23],是预测血液不良反应发生率的主要因素[24];直肠V40和膀胱V40、V50分别是放射性直肠炎和膀胱炎的主要影响因素[25],上述参数中只有膀胱V40的差异具有统计学意义,DeepPlan能够更好地保护膀胱组织。DeepPlan中小肠V20略差,不过其P值(0.049)与阈值(0.05)已较为接近。
DeepPlan和Pinnacle在子野数、MU、CI等参数上的差异有统计学意义,但制定的计划都满足了临床要求。不同放疗系统的算法“特点”不同,即使对相同的病例也会有不同质量的计划,这在临床是可以接受的。比如杨健等[26]证明,对于宫颈癌IMRT,Pinnacle和Eclipse在HI、CI的差异具有统计学意义。Pinnacle和Oncentra在MU和直肠、膀胱的V40等剂量学参数的差异具有统计学意义。
另一方面,不同计划系统之间的算法差异也会影响计划对比的“公平性”。迟子峰等[27]将蒙特卡罗作为第三方平台,对比了4个治疗计划系统的计划质量,证明前列腺癌的IMRT计划更倾向于用Pinnacle和Eclipse治疗,为进一步测试DeepPlan提供了思路。
综上所述,DeepPlan集成了基于共轭梯度法的DAO优化算法,通过GPU加速可以在数分钟内优化得到符合临床剂量要求的放疗计划,DeepPlan优化后的放疗计划在总MU和CI指数上有一定优势,下一步课题组将开展多种治疗方式的DeepPlan临床应用研究。
利益冲突 本研究由署名作者按以下贡献声明独立开展,未因进行该研究接受任何不正当的职务或财务利益,在此对研究的独立性和科学性予以保证
作者贡献声明 程博负责研究的设计、实施以及论文的撰写、修改;方诗杰、任强负责剂量计算的实现;周解平负责数据的收集、统计和分析;曹瑞芬、吴爱东、徐榭、裴曦负责研究设计、技术指导和论文修改
| [1] |
Seco J, Evans PM, Webb S. An optimization algorithm that incorporates IMRT delivery constraints[J]. Phys Med Biol, 2002, 47(6): 899-915. DOI:10.1088/0031-9155/47/6/304 |
| [2] |
Shepard DM, Earl MA, Li XA, et al. Direct aperture optimization:a turnkey solution for step-and-shoot IMRT[J]. Med Phys, 2002, 29(6): 1007-1018. DOI:10.1118/1.1477415 |
| [3] |
Cassioli A, Unkelbach J. Aperture shape optimization for IMRT treatment planning[J]. Phys Med Biol, 2013, 58(2): 301-318. DOI:10.1088/0031-9155/58/2/301 |
| [4] |
杨婕, 张鹏程, 张丽媛, 等. 一种基于梯度信息的直接子野优化算法[J]. 生物医学工程学杂志, 2018, 35(3): 358-367. Yang J, Zhang PC, Zhang LY, et al. A gradient-based direct aperture optimization[J]. J Biomed Eng, 2018, 35(3): 358-367. DOI:10.7507/1001-5515.201609041 |
| [5] |
皮一飞.数字化人体模型开发及其在CT图像自动分割中的应用[D].合肥: 中国科学技术大学, 2018. Pi YF. Development of computational human phantoms and applications to automated CT image segmentation[D]. Hefei: University of Science and Technology of China, 2018. |
| [6] |
霍万里.基于笔形束算法的质子剂量计算方法研究及其在放疗计划系统DeepPlan中的应用[D].合肥: 中国科学技术大学, 2019. Huo WL. Study and application of proton dose calculation of pencil-beam algorithms for the DeepPlan treatment planning system[D]. Hefei: University of Science and Technology of China, 2019. |
| [7] |
Zhang Q, Li X, Wu H, et al. Development of DL-based automatic multi-organ degmentation geature in a new TPS, DeepPlan[C]. American Association of Physicists in Medicine. Scientific Abstracts and Sessions: 61st Annual Meeting and Exhibition. Lancaster, Pennsylvania: 2019, 46(6): E123-E123. DOI: 10.1002/mp.13589.
|
| [8] |
Ren Q, Pan Y, Xu Y, et al. Development of GPU-based collapsed cone dose calculation in a new TPS, DeepPlan[C]. American Association of Physicists in Medicine. Scientific Abstracts and Sessions: 61st Annual Meeting and Exhibition. Lancaster, Pennsylvania: 2019, 46(6): E159-E159. DOI: 10.1002/mp.13589.
|
| [9] |
国家食品药品监督管理局. YY 0775-2010远距离放射治疗计划系统高能X(γ)射束剂量计算准确性要求和试验方法[S].北京: 中国标准出版社, 2010. State Food and Drug Administration. YY 0775-2010 Teleradiotherapy treatment planning system accuracy of dosimetric calculation and test methods for high energy X(γ) beam[S]. Beijing: Standards Press of China, 2010. |
| [10] |
仁达敬. Intel threading building blocks编程指南[M]. 北京: 机械工业出版社, 2009. Ren DJ. Intel threading building blocks[M]. Beijing: China Machine Press, 2009. |
| [11] |
NVIDIA. CUDA toolkit documentation V10.2[Z/OL].[2019-11-28]. https://docs.nvidia.com/cuda/in-dex.html.
|
| [12] |
国家食品药品监督管理总局. YY/T 0889-2013调强放射治疗计划系统性能和试验方法[S].北京: 中国标准出版社, 2013. China Food and Drug Administration. YY/T 0889-2013 Intensity-modulated radiation treatment planning system-Functional performance characteristic and test methods[S]. Beijing: Standards Press of China, 2013. |
| [13] |
Lu WG, Chen ML. Fluence-convolution broad-beam (FCBB) dose calculation[J]. Phys Med Biol, 2010, 55(23): 7211-7229. DOI:10.1088/0031-9155/55/23/003 |
| [14] |
曹瑞芬, 裴曦, 郑华庆, 等. 基于共轭梯度法的调强放疗射束强度分布优化[J]. 原子核物理评论, 2010, 27(2): 212-217. Cao RF, Pei X, Zheng HQ, et al. Beam intensity map optimization based on conjugate gradient in intensity modulated radiation treatment[J]. Nucl Phys Rev, 2010, 27(2): 212-217. DOI:10.11804/Nucl-PhysRev.27.02.212 |
| [15] |
Siochi RA. Minimizing static intensity modulation delivery time using an intensity solid paradigm[J]. Int J Radiat Oncol Biol Phys, 1999, 43(3): 671-680. DOI:10.1016/s0360-3016(98)00430-1 |
| [16] |
李永杰.调强放射治疗中的优化技术研究[D].成都: 电子科技大学, 2004. Li YJ. Study on the optimization algorithms for intensity-modulated radiation therapy[D]. Chengdu: University of Electronic Science and Technology of China, 2004. |
| [17] |
裴曦, 曹瑞芬, 景佳, 等. 调强放射治疗子野权重优化方法研究[J]. 原子核物理评论, 2011, 28(1): 103-108. Pei X, Cao RF, Jing J, et al. A method of segment weight optimization for intensity modulated radiation therapy[J]. Nucl Phys Rev, 2011, 28(1): 103-108. DOI:10.11804/NuclPhysRev.28.01.103 |
| [18] |
Chen Z, D'Errico F, Nath R. Principles and requirements of external beam dosimetry[J]. Radiat Meas, 2007, 41: S2-S21. DOI:10.1016/j.radmeas.2007.01.010 |
| [19] |
Bokrantz R. Multicriteria optimization for managing tradeoffs in radiation therapy treatment planning[D]. Stockholm: KTH Royal Institute of Technology, 2013.
|
| [20] |
邱嵘, 尚凯, 李润霄, 等. 子野面积对宫颈癌IMRT剂量分布的影响[J]. 中华放射肿瘤学杂志, 2016, 25(7): 740-744. Qiu R, Shang K, Li RX, et al. Influence of sub-field area on dose distribution in intensity-modulated radiotherapy for cervical cancer[J]. Chin J Radiat Oncol, 2016, 25(7): 740-744. DOI:10.3760/cma.j.issn.1004-4221.2016.07.016 |
| [21] |
刘小波, 汪冬, 赵云, 等. KylinRay-IMRT与Pinnacle3胸部肿瘤计划剂量学比较分析[J]. 中国医学物理学杂志, 2020, 37(1): 17-21. Liu XB, Wang D, Zhao Y, et al. Dosimetric comparison between KylinRay-IMRT and Pinnacle3 TPS in thoracic tumor plans[J]. Chin J Med Phys, 2020, 37(1): 17-21. DOI:10.3969/j.issn.1005-202X.2020.01.004 |
| [22] |
Isohashi F, Yoshioka Y, Mabuchi S, et al. Dose-volume histogram predictors of chronic gastrointestinal complications after radical hysterectomy and postoperative concurrent nedaplatin-based chemoradiation therapy for early-stage cervical cancer[J]. Int J Radiat Oncol Biol Phys, 2013, 85(3): 728-734. DOI:10.1016/j.ijrobp.2012.05.021 |
| [23] |
Mell LK, Schomas DA, Salama JK, et al. Association between bone marrow dosimetric parameters and acute hematologic toxicity in anal cancer patients treated with concurrent chemotherapy and intensity-modulated radiotherapy[J]. Int J Radiat Oncol Biol Phys, 2008, 70(5): 1431-1437. DOI:10.1016/j.ijrobp.2007.08.074 |
| [24] |
Rose BS, Aydogan B, Liang Y, et al. Normal tissue complication probability modeling of acute hematologic toxicity in cervical cancer patients treated with chemoradiotherapy[J]. Int J Radiat Oncol Biol Phys, 2011, 79(3): 800-807. DOI:10.1016/j.ijrobp.2009.11.010 |
| [25] |
崔彦莉, 王晓贞. 宫颈癌调强放疗不良反应物理性影响因素分析[J]. 河北医科大学学报, 2017, 38(11): 1340-1344. Cui YL, Wang XZ. Analysis of physical influencing factors of adverse reactions of intensity modulated radiotherapy for cervical cancer[J]. J Hebei Med Univ, 2017, 38(11): 1340-1344. DOI:10.3969/j.issn.1007-3205.2017.11.024 |
| [26] |
杨健, 刘颖, 王胜利, 等. 不同治疗计划系统在宫颈癌调强放射治疗中的剂量学比较[J]. 癌症进展, 2019, 17(21): 2561-2564, 2596. Yang J, Liu Y, Wang SL, et al. Dosimetric comparison of different planning systems applied in intensity modulated radiation therapy in the treatment of cervical cancer[J]. Oncol Prog, 2019, 17(21): 2561-2564, 2596. DOI:10.11877/j.issn.1672-1535.2019.17.21.22 |
| [27] |
迟子锋, 韩春, 刘丹, 等. 基于蒙特卡罗方法评估四种治疗计划系统对前列腺癌调强放疗的计划质量[J]. 中华放射肿瘤学杂志, 2011, 20(3): 222-225. Chi ZF, Han C, Liu D, et al. Evaluation of IMRT plans of prostate carcinoma from four treatment planning systems based on Monte Carlo[J]. Chin J Radiat Oncol, 2011, 20(3): 222-225. DOI:10.3760/cma.j.issn.1004-4221.2011.03.015 |
 2020, Vol. 40
2020, Vol. 40


