后装放射治疗具有放射源周边剂量高、剂量梯度变化大的特点，能够在给与肿瘤足够剂量照射的同时保护周围危及器官，它在肿瘤的放射治疗中有不可替代的作用^[1]。传统后装放射治疗计划的设计通常基于固定的计划模板，无法实现患者的个体化治疗，已逐渐被淘汰^[2]。三维后装是现在后装放射治疗技术的主流，逆向优化是三维后装治疗计划系统的基本功能，虽然已有学者对后装治疗中的逆向优化算法进行研究^[3-4]，但是这些算法通常会产生驻留时间变化幅度较大的计划，这种计划存在一些问题。首先是驻留时间较长的位置会受到过高剂量的照射，除非有放射生物学考虑，否则，应避免肿瘤内高剂量照射区域的存在；其次，驻留时间变化幅度越大，剂量分布就越不均匀，治疗计划也越容易受治疗过程中不确定因素的影响^[5]。为控制驻留时间的变化幅度，本研究在前期研究的基础上，实现了一种可以控制驻留时间变化幅度的三维后装逆向优化算法，现报道如下。

1.优化算法：前期研究中，四川省肿瘤医院采用一种的基于梯度下降算法的逆向优化算法(gradient based planning optimization，GBPO)，具体的实现方式和结果在文献[6]中有详细介绍，此处仅做简单描述。

GBPO使用标准的二次目标函数：

式中，t_{m, n}为第m根施源器管道中的第n个驻留位置的驻留时间；p_TAR和p_OARs分别为调节靶区和危及器官权重的参数；D₀为靶区处方剂量或危及器官的剂量限制；D_i为第i个体元的剂量；H为阶跃函数。对于靶区，当D_i<D₀时为1，否则为0；对于危及器官，当D_i>D₀时为1，否则为0。

第i个体元的剂量D_i通过下式计算：

式中，N_M为施源器管道总数；N_N为单根管道中放射源驻留位置总数；d_{m, n}为单位时间的第m根施源器管道中的第n个驻留位置对第i个体元的剂量率贡献，其计算方式见文献[7]。

为了可以根据临床需求调节驻留时间的变化幅度，本研究对上述算法进行了改进，在目标函数中增加一个控制驻留时间变化幅度的项，用驻留时间调制因子(dwell time modulation factor，DTMF)调节驻留时间的变化幅度，改进后GBPO的目标函数变为：

式中，p_SOU为驻留时间调制因子DTMF；t_{m, min}为第m根施源器管道中最小的驻留时间。

2.患者数据：统计本院某医生从2018年7月至2018年9月使用三管施源器治疗的患者15例，患者中位年龄52岁(35~70岁)，肿瘤体积的平均值为53.65 cm³(35.68~80.45 cm³)。在Oncentra V4.3计划系统上勾画靶区和危及器官，危及器官包括膀胱、直肠和小肠。处方剂量是高危临床靶区(HR-CTV) 90%的体积受到6 Gy的照射。

3.计划设计：本研究中每例患者都采用两种计划：商用计划系统(Oncentra V4.3)中以模拟退火逆向计划(inverse planning simulated annealing，IPSA)算法设计的计划和本研究报道算法设计的基于梯度的计划优化(GBPO)计划。所有计划放射源的步进长度均为0.25 cm，剂量计算网格均为0.1 cm×0.1 cm×0.1 cm。两种计划使用相同的驻留点位置和个数。

IPSA计划可以根据参考靶区自动确定放射源驻留位置，优化中所有患者都使用了相同的初始参数：HR-CTV为参考靶区，最小剂量6 Gy，权重100；膀胱、直肠和小肠的表面最大剂量为4 Gy，权重80。IPSA中的驻留时间变化控制(dwell time deviation constraint，DTDC)参数会影响优化结果^[8]，本研究中IPSA计划的DTDC值均为0.4。

GBPO计划不改变IPSA计划的驻留点位置和个数，每个驻留点的初始驻留权重都为1，迭代过程中驻留点权重的最小值设定为0.000 001。所有GBPO计划都迭代50次，GBPO优化使用的初始参数为：HR-CTV最小剂量6 Gy，权重100；膀胱、直肠和小肠的最大剂量为4 Gy，权重80。这些参数也是确定GBPO中调节驻留点时间变化权重参数p的优化参数。在与IPSA计划进行对比时，如果GBPO采用初始参数得到的优化结果不满意，就适当地调节初始参数，直至得到满意的优化结果。本研究中GBPO的DTMF统一为10。

4.计划评估：通过剂量体积直方图(dose volume histogram, DVH)参数评估GBPO计划和IPSA计划的差异，统计HR-CTV的D_100%、V_150%，危及器官的D_{0.1 cm³}、D_{1 cm³}和D_{2 cm³}。所有计划都归一到处方剂量，即HR-CTV D_90%=6 Gy。

5.统计学处理：利用SPSS 19.0软件对DVH参数进行统计分析。计量资料满足正态分布，数据以x±s 表示。将GBPO计划与IPSA计划进行配对样本t检验，P < 0.05为差异具有统计学意义。

1.调节驻留时间变化幅度的参数：图 1为采用GBPO算法优化的15例患者治疗驻留时间标准差，可以看出，调节驻留时间变化幅度的参数p_SOU在增加到100以后，驻留时间标准差无明显的变化，所以在使用GBPO算法优化宫颈癌腔内后装治疗计划过程中，p_SOU的值不建议超过100。

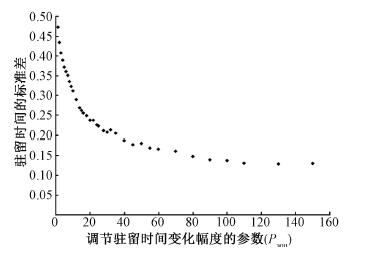
图 1 15例患者驻留时间的标准差随调节驻留时间变化幅度的参数变化图 Figure 1 Variation of dwell time standard deviation with dwell time modulation factor for 15 patients

2.靶区和危及器官参数对比：表 1对比了15例患者IPSA计划和GBPO计划靶区和危及器官的DVH参数，GBPO计划的D_100%高于IPSA计划，两种计划之间其他DVH参数的差异无统计学意义(P>0.05)，使用GBPO可以得到与IPSA相似的计划质量。

表 1(Table 1)

表 1 15例患者的DVH参数对比 Table 1 Comparison of DVH parameters for 15 patients 计划 HR-CTV 膀胱 直肠 小肠 D100% D90% V150% D0.1 cm3 D1 cm3 D2 cm3 D0.1 cm3 D1 cm3 D2 cm3 D0.1 cm3 D1 cm3 D2 cm3 GBPO 3.63±0.36 6.00±0.00 55.59±3.17 5.84±0.84 5.07±0.65 4.74±0.61 5.64±0.72 4.49±0.61 3.99±0.64 4.63±1.31 3.68±1.08 3.26±0.99 IPSA 3.53±0.34 6.00±0.00 55.63±4.42 5.82±0.89 5.06±0.71 4.75±0.65 5.65±0.82 4.52±0.67 4.02±0.67 4.56±1.37 3.65±1.12 3.24±1.02 t值 2.45 -0.14 0.18 0.21 -0.19 -0.23 -0.57 -0.68 1.22 0.95 0.39 P值 0.02 0.95 0.65 0.95 0.91 0.96 0.44 0.21 0.30 0.44 0.52   注：DHV.剂量体积直方图；HR-CTV.高危临床靶区；GBPO.基于梯度的计划优化；IPSA.模拟退火逆向计划

表 1 15例患者的DVH参数对比 Table 1 Comparison of DVH parameters for 15 patients

商用的逆向优化算法IPSA和HIPO(hybrid inverse planning optimization)都提供了控制驻留时间变化幅度的参数，通过调整参数，可以在获得令人满意的临床计划参数的同时驻留时间变化幅度也不会很大。与上述两种商用逆向优化算法不同，本文报道本中心已实现的一种控制驻留时间变化幅度的方法。通过15例宫颈癌患者的研究，结果表明该算法能优化出良好的剂量分布，达到与商用计划系统相似的优化结果。

IPSA和HIPO可产生质量相似的治疗计划^{[2, 10]}。IPSA中驻留时间调节参数是DTDC，它是一个用户输入的参数，用于约束单个驻留时间相对于平均驻留时间的上限，不考虑驻留时间低于平均驻留时间的情况。DTDC为0时表示优化无驻留时间约束，DTDC在[0~1.0]的范围内以0.1的步长变化，为1.0时，驻留时间最均匀。DTDC可有效减小长驻留时间。HIPO中调节驻留点权重变化的参数是DTGR(dwell time gradient restriction)，它避免了相邻驻留位置之间的大的驻留时间差异，因此也避免了存在可能导致热点的长驻留时间之间的位置。DTGR参数与DTDC一样，在0~1.0的范围内以0.1的步长变化，用户输入DTGR参数被转化为优化目标中的相邻驻留点之间的时间梯度变化函数^[9]。增加DTGR值，就可以迫使优化软件避免出现单个驻留时间非常高或非常低的情况，由于DTGR考虑相邻驻留时间的变化，所以在不需要驻留的位置，由于DTGR的作用，也可能会有短驻留时间的出现。

本算法调节驻留时间变化幅度的原理与IPSA和HIPO不同，具体体现在：①在优化目标函数中采用最小驻留时间，而不使用平均驻留时间。原因是从计划质量考虑，某些驻留位置可能不适合放射源驻留，在这种情况下，尽可能地保留最小驻留时间。添加驻留时间优化目标项的目的是让较长的驻留时间变短。因为保留了最小的驻留时间，所以在增加了p_SOU后，驻留时间标准差也不会为0。②本算法未对驻留权重p_SOU归一。原因是本研究只采用了根治性宫颈癌这一种病例进行测试，未考虑其他类型的病例，适合一种病例的驻留权重归一参数不一定适合另一种病例，归一后在临床实际应用中存在局限性。另外，参照IPSA和HIPO的归一方法归一后，只有11个权重值，这会让可调节的空间变小。如果不进行归一，可以根据需要设定不同的权重，可调节空间更大。

对于根治性宫颈癌患者病例，当驻留时间权重参数p_SOU超过100后，驻留时间标准差的变化就不大，因此，临床应用中可根据实际需要在0~100之间选择p_SOU值。需要说明的是，本研究的结果是基于特定的优化参数，如果更改了优化参数，驻留时间标准差随p_SOU参数变化的趋势可能会有一定的变化。另外，不同病例的驻留时间标准差随p_SOU参数变化的趋势可能不同，因此，其他病例在使用p_SOU前，也应进行相应的研究，找出适合某种病例的值。采用其他病例对本算法进行验证和研究是下一步要开展的工作。

综上所述，本文报道了一种可以控制驻留时间变化幅度的三维后装逆向优化算法GBPO，对于根治性宫颈癌患者常用的Fletcher施源器，该算法能达到与商用优化算法IPSA相近的结果，此算法可以集成在三维后装治疗计划系统中，提升国产后装治疗计划系统的竞争力。

利益冲突  所有作者均声明没有利益冲突

志谢 本研究得到了成都市科技厅重点研发支撑计划资助(2019-YF09-00095-SN)

作者贡献声明  毕斌负责论文撰写；黎杰、王培、康盛伟、唐斌、汤婷王先良负责课题设计及最终修改