粒子治疗是放射治疗手段之一，主要包括质子治疗和碳离子治疗。相对于传统的放射治疗手段，粒子束可以在射程末端释放数倍于坪区的能量，因此能够在给予靶区剂量的同时，更好地保护正常组织。粒子治疗，尤其是质子治疗，在国内外发展迅速，临床需求日益增加，也使得质子束流用于科研和质量保证的时间十分有限。蒙特卡罗(Monte Carlo，MC)模拟方法作为一种模拟质子束流的手段，可以在一定程度上，作为质子束流测量的替代方案来进行对质子束流方面的研究工作。蒙特卡罗模拟技术可以模拟粒子在介质中的输运过程，在质子治疗中的应用主要包括设备调试^[1]、剂量计算^[2]、建立剂量验证模型^[3-4]、质子相对生物效应(relative biological effectiveness，RBE)模型计算^[5-6]、质子治疗中次级中子剂量计算^[7-8]和质子治疗设备屏蔽计算^[9-10]等。

上海市质子重离子医院(SPHIC)的质子束流是基于点扫描技术的笔形束，本研究的目的是基于治疗机头几何设置及SPHIC的质子束流测量数据，建立点扫描质子束流治疗机头蒙特卡罗模拟模型，并探讨该模型在治疗计划验证中的应用。

1.蒙特卡罗程序：模拟计算采用的是蒙特卡罗FLUKA程序^[11-12]。FLUKA程序中加强了对粒子的输运模拟能力，还支持对大量复杂的几何体进行建模，可以导入CT数据生成体素模型，导入DICOM计划、剂量、靶区等数据，大大增强了其在放射医学中的应用能力^[13]。本研究利用FLUKA模拟程序2011.2x版本，模拟质子在介质中的输运过程。采用FLUKA预设的PRECISIO模式来设置模拟的物理过程。在该模式下，中子截止能量设置为10^-5 eV，其他粒子输运的截止能量为100 keV。

2.计算硬件配置和并行计算：蒙特卡罗模拟软件的仿真速度主要由软件架构和硬件环境决定。本研究使用的是专门用于临床剂量蒙特卡罗模拟计算的多处理器并行计算服务器集群。该集群由1台主机和3台节点机构成，总CPU数量达到112个。FLUKA程序本身并不直接支持并行计算，但可以利用FLUKA的界面软件FLAIR，生成数个模拟的输入文件，并给予各输入文件不同的初始随机数，再利用LINUX的shell脚本执行这些输入文件，从而实现间接并行计算，提高计算效率。

3.束流输运模式与治疗机头结构：SPHIC采用同步环加速器，粒子束流经过离子源、直线加速器和同步环加速器加速至需要的能量，经高能输运线引出，至x、y偏转磁铁后，进入治疗机头。治疗机头包括真空管，真空窗(vacuum window，VW)，两个用于束斑和位置测量的多丝正比室(multi wire proportional chambers，MWPCs)，两个用于剂量测量的电离室(ion chambers，ICs)，一个用于流强测量的探测器(intensity monitor，IM)以及束流路径上的其他设备，如脊型过滤器(ripple filter，RF)和降能器(range shifter，RS)。

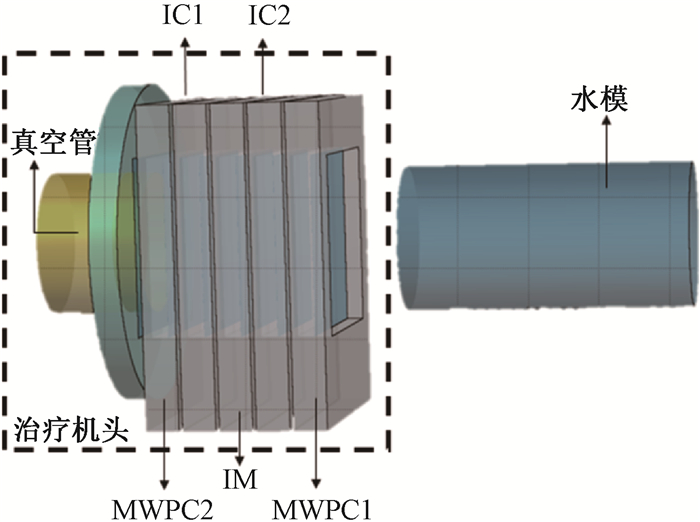
4. SPHIC的粒子治疗机头蒙特卡罗模型：结合SPHIC粒子治疗机头的几何结构，建立了治疗机头的蒙特卡罗模型(图 1)，具体建模方式与Parodi等^[14]阐述的方法相同。为了能够快速建立模型，对VW，MWPCs和ICs进行了水等效简化处理，其等效水深分别为360、230和160 μm。其中，MWPCs还包含3 μm钨层，以提高蒙特卡罗模型对质子束流散射、特别是低能质子散射的模拟精度。模型对上述设备在治疗机头内的相对位置保持不变。RF是用于对碳离子的布拉格峰展宽，由于本研究模拟的是质子束流，因此实际模拟中没有在束流路径上设置RF。

注：IC.电离室；MWPC.多丝正比电离室；IM.集成监控电离室 图 1 FLUKA模型中治疗机头的几何设置 Figure 1 Geometry of treatment nozzle in FLUKA model

5. SPHIC质子束流的测量和模拟：SPHIC粒子束流使用的是主动的点扫描技术，通过调节束流能量、束斑大小、束流强度，引出粒子束流进行治疗。蒙特卡罗模拟束流的输入参数包括束流标称能量，能谱(高斯分布)，x、y方向分别的束斑，束流的角分布等。

6.积分深度剂量测量和模拟：SPHIC临床上使用的质子束流共包括252个能量层，能量范围为48~221 MeV，对应等效水深度为20~310 mm。使用PTW^Ⓡ寻峰设备(德国PTW PeakFinder)对质子束流的积分深度剂量分布(integral depth-dose profile，IDD)进行测量，采用与盛尹祥子等^[15]束流射程测量的类似方法，PeakFinder被放置于束流方向上，距离真空窗342 mm位置，选择测量了48.08~21.07 MeV等15个能量的积分深度剂量。

FLUKA的模拟中，在与上述测量相同的位置放置水模体，模拟统计直径为8 cm的区域内不同水深度的相对剂量。通过调节模拟质子束流的标称能量和能谱分布来匹配测量结果。对比分析了测量和模拟的质子束流射程末端90%剂量深度值(R₉₀)和射程末端80%至20%跌落(R_80~20)之间的差异。

7.束斑大小的测量和模拟：SPHIC临床使用的质子束流束斑大小从8到35 mm不等，随能量增加而降低。利用EDR2胶片对质子束流束斑进行测量，将胶片放置于束流方向上等中心点处，距离真空窗1 400 mm处。测量束流的侧向扩展，通过扫描胶片进行分析，获取束流在x、y方向上的半高宽(full width half maximum，FWHM)，即束斑大小。

FLUKA模拟中，质子源设置在偏转磁铁位置，模拟束流经过束流路径上的材料后在距离真空窗1 400 mm处空气中的侧向展宽。通过调节模拟的质子源束斑大小和形状，从而与测量得到的数据进行匹配。

8. FLUKA模拟水箱验证计划：通过Syngo^Ⓡ治疗计划系统制定扩展布拉格峰宽度(spread-out Bragg peak，SOBP)8 cm，深度11 cm的均匀的水箱验证计划。利用FLUKA程序对上述物理计划和几何设置进行模拟。模拟需采用source.f文件来定义质子源^[12]。通过对质子束流的能量和位置按物理计划中的指定比例进行抽样，统计侧向和深度二维剂量分布。对FLUKA模拟和TPS计算结果进行对比。

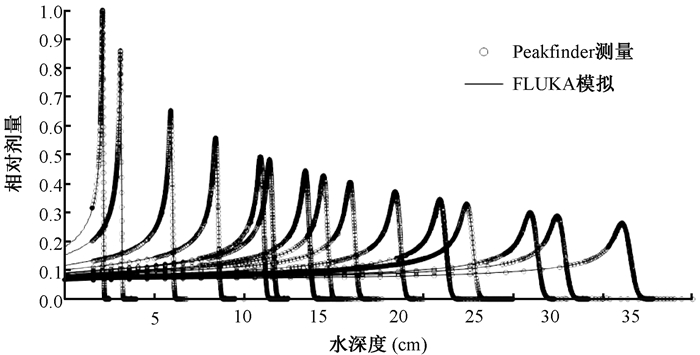
1.积分深度剂量分布(IDD)：测量和模拟各能量的积分深度剂量分布见图 2。对测量和模拟结果分别参照最大值进行了归一。从图 2中可知，测量和模拟的结果符合良好。对于射程末端90%剂量深度值(R₉₀)，各能量下测量和模拟的偏差绝对值≤0.5 mm，平均偏差为(-0.08±0.2)mm，相对偏差≤0.85%。列于表 1。而对于射程末端80%至20%跌落，各能量的测量和模拟的偏差绝对值在0.1 mm以内。

图 2 质子各能量水中积分深度剂量的测量和模拟 Figure 2 Comparison of IDD for different proton energies between measurement and simulation

表 1(Table 1)

表 1 质子各能量射程末端90%剂量深度值R90的测量和模拟结果 Table 1 Comparison of the distal range of 90% for different proton energies between measurement and simulation 能量 (MeV) 测量结果 (cm) FLUKA模拟 (cm) 绝对偏差 (cm) 相对偏差 (%) 48.08 2.134 2.129 0.005 0.23 59.82 3.141 3.139 0.002 0.06 85.67 5.857 5.907 0.050 0.85 104.49 8.484 8.474 0.010 0.12 121.08 11.003 11.005 0.002 0.02 124.20 11.510 11.503 0.007 0.06 136.16 13.525 13.506 0.019 0.14 141.87 14.539 14.524 0.015 0.10 150.14 16.038 16.031 0.007 0.04 163.27 18.567 18.545 0.022 0.12 175.72 21.076 21.033 0.043 0.20 182.44 22.579 22.575 0.004 0.02 199.03 26.142 26.115 0.027 0.10 205.68 27.647 27.626 0.021 0.08 221.07 31.283 31.282 0.001 0.00 注：绝对偏差=|模拟值-测量值|；相对偏差=绝对偏差/测量值

表 1 质子各能量射程末端90%剂量深度值R90的测量和模拟结果 Table 1 Comparison of the distal range of 90% for different proton energies between measurement and simulation

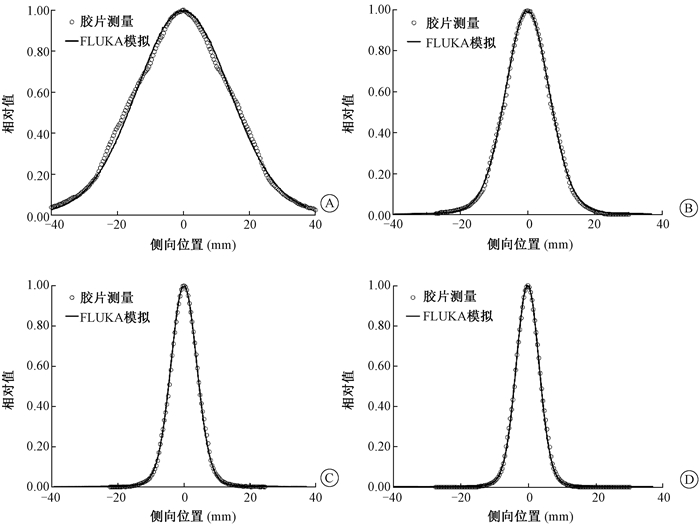
2.束斑大小：测量和模拟了15种能量的质子束流在空气中侧向展宽。图 3对比了其中4个能量(48.08、104.49、182.44和221.07 MeV)经归一后的计算和测量结果。由于对FLUKA模拟时，x和y方向采用相同的高斯分布，因此这里只列x方向的结果。对所有质子束流，测量与模拟的FWHM的绝对偏差最大值为0.45 mm(质子能量59.82 MeV时)，平均偏差为(-0.02±0.22)mm，相对偏差最大值为2.45%(质子能量121.08 MeV时)。

图 3 不同能量质子束斑x方向侧向展宽曲线A. 48.08 MeV；B. 104.49 MeV；C. 182.44 MeV；D. 221.07 MeV Figure 3 Comparison of x direction lateral profiles for proton spots with different energies A. 48.08 MeV; B. 104.49 MeV; C. 182.44 MeV; D. 221.07 MeV

3. FLUKA模拟验证计划：对扩展布拉格峰的深度剂量分布、侧向展宽分布的TPS计算数据和FLUKA模拟数据进行了比较。采用γ分析^[16]方法对模拟和TPS计算数据进行比较。所有剂量分布数据归一到处方剂量(2 Gy)，采用3 mm，3%的γ分析标准，两截面通过率分别为98.8%和99.1%，采用2 mm，2%的γ分析标准，两截面通过率分别为90.5%和92.3%。平均偏差0.024 Gy (1.2%)，最大点剂量偏差不超过5%。其中，靶区中心区域吻合度较高，偏差较大的点集中在靶区边缘，主要因为调强的质子治疗计划系统在制定治疗计划时，会在靶区边缘设置更多的粒子数以提高靶区边缘剂量梯度。

对治疗机头和束流参数的模拟是蒙特卡罗剂量计算的首要步骤，无论是对分析算法的改进研究，还是对预期剂量分布进行评价，还是制定蒙特卡罗治疗计划，或是建立相空间文件，都需要开展的第一步研究。蒙特卡罗模拟有助于新设备的设计，束流质量保证(quality assurance，QA)以及剂量验证等工作。利用蒙特卡罗的模拟数据，可以作为输入参数，对粒子治疗计划系统进行调试。

本研究利用蒙特卡罗计算软件FLUKA，通过设置适当的几何和物理参数，模拟了SPHIC的质子束流在放射治疗中的输运过程。为了使模拟结果接近现实情况，所建立的治疗机头蒙特卡罗模型的内部设备在几何尺寸和设备相对位置上与实际情况一致。设备材料采用了水等效模型，对MWPC还增加了钨丝层，最大限度的匹配实际情况。

Grevillot等^[17]利用Geant4建立了点扫描质子束流模型并进行了测量验证。得到模拟和测量的质子束流射程和束斑FWHM最大偏差分别为0.6和0.2 mm。Almhagen等^[18]利用TOPAS建立了IBA笔形束质子模型，模拟了34个能量的质子束流参数并与测量结果进行对比，结果显示质子束流的射程和束斑FWHM偏差均在0.25 mm以内。本研究中利用FLUKA模拟了点扫描质子束流，模拟得到的各能量质子束流的射程末端90%剂量深度值与测量值偏差不高于0.5 mm/0.85%，束斑半高宽最大偏差不超过0.45 mm/2.45%。上述偏差均在临床上可以接受的范围以内，并且低于质子束流参数测量的偏差限值。模拟结果说明，通过调整质子源的能量和束斑等参数，该治疗机头蒙特卡罗模型模拟结果可以与束流的测量结果较好的匹配。

对扩展布拉格峰的模拟结果说明，该治疗机头FLUKA模型可以精确地模拟质子束流在水中的输运情况，平均剂量偏差不超过1.5%，γ分析通过率均超过90%(2 mm，2%标准)。本模型中采用的初始束斑为高斯分布，束流平行出射，忽略了束流的发散角。FLUKA程序可以采用用户自定义的source.f文件，给予采样粒子方向余弦，从而定义粒子出射的发散角^[19]，该模拟方法对模拟精度的改进效果需要进行进一步的研究。

为了得到更加精准的计算结果，对积分深度剂量分布的模拟计算中，使用了超过100万个初始粒子，从而将计算结果的统计误差降低到1%以内，单次模拟所需单CPU时间在1 h左右。而对于束斑大小的模拟计算，由于设置的读数区域比较小，且计数是在空气中进行的，需要近700万初始粒子数才能将关键区域的统计误差降至1%以内。本次模拟计算并未使用降低方差的方法，因此模拟所需单CPU时间较长。但采用了多CPU并行计算方法，从而大大降低了实际计算时间，提高了模拟效率。