重离子放疗将布拉格峰集中在肿瘤区域,利用其高传能线密度特性杀死肿瘤,同时利用坪区和末端低剂量特性降低正常组织剂量,但由于离子射程不确定客观存在[1],当布拉格峰位置与计划值发生偏差时肿瘤和正常组织接受的实际剂量可能发生巨大变化,因此定位布拉格峰在体内实际位置对于重离子精准放疗意义重大[2-3]。然而,现有以正电子发射计算机断层成像为主的布拉格峰验证技术还并不能完全满足临床需求,无法做到快速精准定位布拉格峰[4]。重离子到达布拉格峰时传能线密度会显著升高,这导致峰周围介质温度短时间内迅速升高,进而产生热声学效应[5-6],这一特性让通过声学探测实现布拉格峰快速定位成为可能[3]。Kellnberger等[7]和Assmann等[8]利用超声探测器来定位低能质子布拉格峰位置,具有成像速度快定位精度高等特点,但该研究中质子声信号频率高幅度强较易探测。接着Lehrack等[9]验证利用截止频率更低的声探测器定位同步回旋加速器产生的高能质子束流布拉格峰,结果显示该系统同样可实现亚毫米定位精度,但由于使用的质子能量更高,信号频率和幅度显著下降,需较高剂量才能实现精准定位。以上研究中质子流强大,持续时间短,研究表明流强与声信号幅度成正比[10-11],而实际临床离子束流流强低,持续时间长,相关研究少,此外碳离子布拉格峰传能线密度远高于质子,其离子声信号可能与质子存在差异。本研究将系统验证一种声学探测探测质子碳离子布拉格峰声信号的可行性。
材料与方法1.整体框架:系统框架见图 1,质子或碳离子从治疗机头引出后进入水箱,在声学探测器前方产生布拉格峰声信号,声信号被紧贴在水箱后方薄膜上的声学探测器获得,信号经过放大和滤波输入到示波器显示。

|
图 1 声学探测系统框架 Figure 1 The framework of acoustic detection system |
2.束流参数:本研究采用德国西门子提供的IONTRIS离子放疗系统,包含一套同步加速器和4个固定野治疗机房。该系统可产生点扫描质子和碳离子,其中质子流强从5.0×107~2.6×109粒子/s,碳离子流强从1.3×106~6.5×107粒子/s。
3.水箱:水箱为圆柱状,外径为66.0 mm,内径为53.0 mm,长为116.0 mm,材质为亚克力,水箱靠近束流近端利用亚克力材质瓶盖密封,为了降低亚克力对于声信号的反射和折射,远端采用特氟龙塑料薄膜覆盖,声学探测器利用热熔胶固定在薄膜中间,与束流垂直,薄膜与探测器空隙利用明胶填充,水箱水等效深度使用寻峰设备(Peakfinder,PTW,德国西门子)经高能质子测定为119.0 mm。
4.声学探测器:超声设备无法探测到临床质子产生的声信号。与Assmann等[8]研究相比,本研究质子最大流强仅为该研究最小流强的0.1倍,需采用更高灵敏度探测器。基于预试验Lehrack等[9]和Sulak等[10]研究,使用了探测频率更低的探测器(MAX9812,中国),该探测器可探测频率为10 Hz到20 kHz,灵敏度-44 dB,信噪比60 dB,具有灵敏度高,信噪比高,体积小和造价低等特点。束流产生的声压会导致探测器电容值发生改变从而产生电信号。
5.摆位与测量:由于水箱大小和探测器摆位为固定值,只能通过改变入射离子初始能量从而使布拉格峰到探测器距离Dpd发生改变来测试该探测器的测量范围。基于类似原因,在测量离子布拉格峰横向半高宽时,在Dpd固定情况下,在水平或竖直方向上移动离子束斑中心位置来实现离子半高宽测量。研究质子和碳离子流强,Dpd与信号幅度关系时的束流参数列于表 1,其中质子和碳离子在等中心处半高宽分别为12.9 mm和5.6 mm,质子和碳离子出束所用总粒子分别为5.0×109和5.0×107。
|
|
表 1 质子碳离子流强,Dpd与信号幅度关系束流参数 Table 1 Parameters used for proton and carbon measurements |
6.信号输入与显示:声学探测器信号首先通过探测器自带运算放大器进行信号放大和滤波,然后输入到示波器中显示,示波器显示频率为250 Hz,信号幅度最小单位为1 mV,示波器采用4倍背景噪声抑制技术。
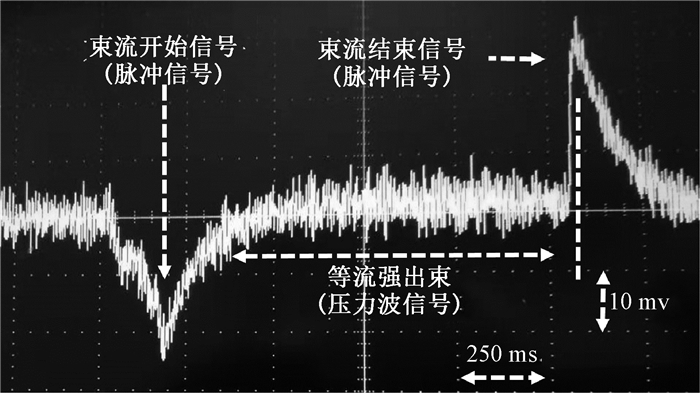
7.数据获取:实验采用等流强持续数秒的离子束流,因此探测系统只有在束流开始和束流结束时探测到脉冲信号,如图 2。分析中分别采用束流开始和束流结束时产生的脉冲信号(下称束流开始信号和束流结束信号)幅度作为分析数据。布拉格峰横向半高宽定义为束斑在布拉格峰区域横向最大半高宽。测量时,首先将原始测量数据减去本底后在Matlab(R2015B,美国Mathworks)中采用高斯方法拟合获得sigma值,接着使用公式半高宽等于sigma×2.355获得布拉格峰横向半高宽,然后与计划系统模拟获得的束斑布拉格峰区域横向最大半高宽进行对比。
|
图 2 典型临床质子碳离子布拉格峰声信号 Figure 2 Typical acoustic signal of clinical proton and carbon ion Bragg-peak |
8.统计学处理:信号可重复性可通过比较相同参数不同时段15次测量结果获得,使用配对t检验进行统计分析,P < 0.05为差异有统计学意义。
结果1.信号重复性检验:对束流开始和束流结束信号进行t检验,两者差异无统计学意义(P>0.05)。
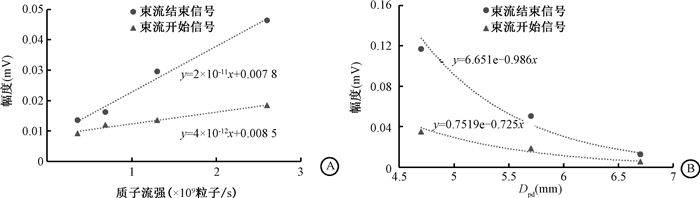
2.质子流强,Dpd与信号幅值关系:随着流强增加,束流开始和束流结束信号幅值线性递增,但束流结束信号更敏感(图 3)。Dpd从4.7 mm变化到6.7 mm,该系统均可获得满意输出;但信号幅度随Dpd指数下降,尤其是束流结束信号(图 3)。
|
A.流强与幅值;B. Dpd与幅值 图 3 流强,Dpd与信号幅值关系 A. Beam intensity versus magnitude of signal; B. Dpd versus magnitude of signal Figure 3 Beam intensity or Dpd versus magnitude of signal |
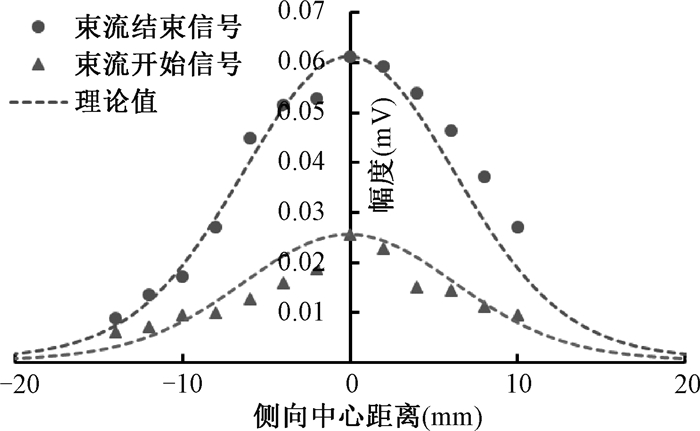
3. 125.43 MeV质子在水平方向布拉格峰横向半高宽测量结果:该质子能量在布拉格峰位置横向理论半高宽为15.7 mm,束流开始信号测得束流横向半高宽为17.6 mm,比理论值高11.7%,束流结束信号测得横向束流半高宽为17.2 mm,比理论值高9.3%。图 4虚线为束斑理论水平方向横向剂量分布,实心点为测量数据,将理论水平方向剂量分布归一到测得数据最大值并叠加显示,碳离子也采用相同方法;测量显示在低信号区域,结果受噪声影响较大;其他测量条件与流强测量一致。
|
图 4 质子布拉格峰横向半高宽测量 Figure 4 The measurements of lateral full width at half max of a proton Bragg-peak |
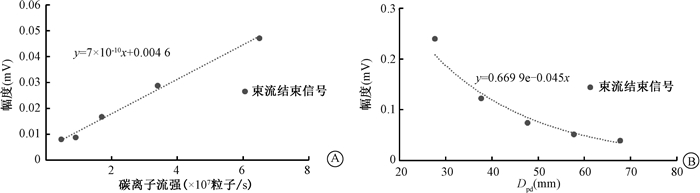
4.碳离子流强,Dpd与信号幅值关系:质子测量结果表明,束流结束信号信噪比更高,因此碳离子仅采用束流结束信号测量结果。与质子类似,碳离子流强与束流结束信号幅值随流强增加呈线性增加(图 5)。碳离子Dpd远大于质子Dpd,其Dpd从27.7 mm到67.7 mm,束流结束信号幅值呈指数下降,虚线为拟合值(图 5)。
|
A.流强与信号幅值;B. Dpd流强与信号幅值 图 5 碳离子流强,Dpd与信号幅值关系 A. Beam intensity versus magnitude of signal; B. Dpd versus magnitude of signal Figure 5 Beam intensity and Dpd versus magnitude of signal of carbon ion beam |
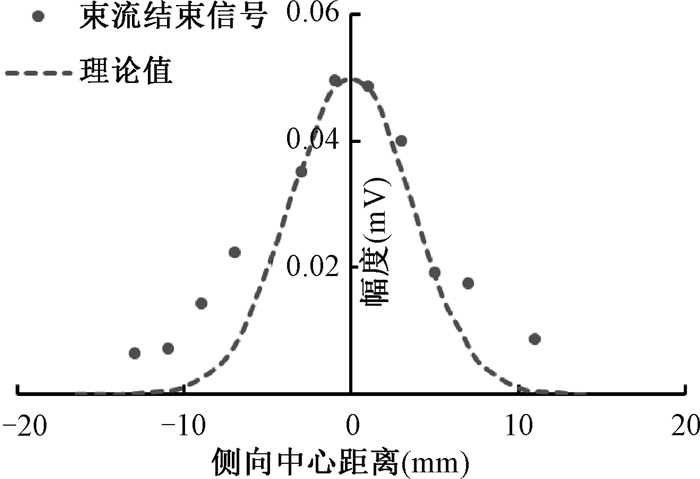
5. 178.89 MeV/u碳离子在水平方向横向半高宽测量结果:该能量碳离子在布拉格峰位置横向理论半高宽为8.5 mm,根据束流结束信号测得束流横向半高宽为12.5 mm,比理论值高45.6%。图 6虚线为理论束斑水平方向横向剂量分布,实心点为测量数据,结果显示信号受噪声影响比质子更大;其他测量条件与流强测量一致。
|
图 6 碳离子布拉格峰横向半高宽测量 Figure 6 The measurements of lateral full width at half max of carbon ion Bragg-peak |
讨论
提高信噪比是离子布拉格峰声学研究的重要课题,可通过提高束流流强,降低束斑大小和选择合适探测器等综合实现[10]。本研究及Sulak等[10]和Kipergil等[11]研究均表明,随着流强降低,产生声信号幅度也会线性降低,需使用灵敏度更高探测频率更宽的声学探测器。Assmann等[8]使用了20 MeV质子,与之相比本研究质子流强仅为其十万分之一到十分之一,同时本研究质子布拉格峰传能线密度也显著低于该研究。由Sulak等[10]研究可知,本研究信号强度要显著低于Assmann等[8]的研究,因此本研究未尝试使用兆赫兹级超声探测器。Lehrack等[9]在针对临床质子布拉格峰声信号研究中,根据能量增加布拉格峰传能线密度下降事实,使用了探测频率更低的探测器。本研究选择探测器方法符合以上研究思路。
与以往研究中质子大都由回旋加速器产生不同,本研究中质子和碳离子由同步加速器产生,没有经过任何散射设备或降能设备,离子束流能量展宽更窄。Yoshinori等[12]研究表明,当质子经过散射设备后其布拉格峰产生声效应更复杂,不利于布拉格峰声学探测的研究。以往多数研究采用束流时间仅为纳秒到微秒级质子脉冲,由于声信号幅度与脉冲持续时间成反比[13],因此会产生更显著声脉冲信号有利于探测。而临床点扫描质子和碳离子束流流强低,产生相同剂量需更长时间,流强在出束期间保持恒定,仅会在束流开始和束流结束产生脉冲信号。因此,本研究尝试使用束流开始和束流结束产生声信号幅值来表示声信号幅度,统计研究证明该方法有效。
已有离子声信号计算公式[3, 8, 14]假设一束短质子脉冲(1 ns~10 μs)释放所有能量导致介质的温度短时快速升高从而产生脉冲声信号,其特点是只有一个脉冲信号由束流直接产生,其次所有离子剂量与脉冲幅度相关。但如本研究所示,由同步加速器引出的临床质子和碳离子束流流强低,持续时间长(通常>250 ms),束流开始和束流结束分别产生两个脉冲信号而不是一个脉冲信号,进而无法将所有离子产生的剂量与声信号的某个脉冲或整体关联,这导致先前的计算公式无法直接用于该种声信号的计算。未来需做进一步测量与验证,并基于测量数据对现有声信号计算公式进行改进。
目前还没有针对碳离子声学研究的详细报道,本研究显示碳离子布拉格峰声学信号特性与质子类似,但碳离子布拉格峰声信号幅度要显著强于质子布拉格峰声信号,Dpd显著增长。这可能与碳离子布拉格峰具有显著高传能线密度和更高峰谷比相关,因此,相关声学研究对声探测器灵敏度要求显著低于质子。这可能会让碳离子声学探测在临床上更容易实现,未来可应用该特性对接受碳离子放疗的患者进行布拉格峰在线定位:通过基于现有测量数据进行理论计算得出声信号的范围和强度,将该理论结果与测量值进行对比可实现离子束流布拉格峰位置的实时定位。但碳离子尾端剂量会显著增加探测系统噪声,降低信噪比,未来需进一步降低噪声对于碳离子测量结果影响。
志谢 感谢上海市质子重离子医院放射物理科其他同事对于本研究的建议和协助利益冲突 无
作者贡献声明 王巍伟负责设计研究方案,并起草和修改论文;陈帜负责测量和处理数据,并协助修改论文;Kambiz Shahnazi指导研究方案设计;黄志杰对研究方案设计和结论进行理论指导;盛尹祥子协助起草和修改论文
| [1] |
Paganetti H. Range uncertainties in proton therapy and the role of Monte Carlo simulations[J]. Phys Med Biol, 2012, 57(11): R99-117. DOI:10.1088/0031-9155/57/11/R99 |
| [2] |
Kraan AC. Range verification methods in particle therapy:underlying physics and monte carlo modeling[J]. Front Oncol, 2015, 5: 150. DOI:10.3389/fonc.2015.00150 |
| [3] |
Parodi K, Assmann W. Ionoacoustics:A new direct method for range verification[J]. Mod Phys Lett A, 2015, 30(17): 1540025. DOI:10.1142/S0217732315400258 |
| [4] |
Dendooven P, Buitenhuis HJ, Diblen F, et al. Short-lived positron emitters in beam-on PET imaging during proton therapy[J]. Phys Med Biol, 2015, 60(23): 8923-8947. DOI:10.1088/0031-9155/60/23/8923 |
| [5] |
Bowen T, Nasoni RL, Pifer AE. Thermoacoustic imaging induced by deeply penetrating radiation[M]//Kaveh M, Mueller RK, Greenleaf JF. Acoustical Imaging: vol 13. Boston: Springer, 1984: 303.
|
| [6] |
Albul VI, Bychkov VB, Vasil Ev SS, et al. Acoustic field generated by a beam of protons stopping in a water medium[J]. Acoust Phys, 2005, 51(1): 33-37. DOI:10.1134/1.1851626 |
| [7] |
Kellnberger S, Assmann W, Lehrack S, et al. Ionoacoustic tomography of the proton Bragg peak in combination with ultrasound and optoacoustic imaging[J]. Sci Rep, 2016, 6: 29305. DOI:10.1038/srep29305 |
| [8] |
Assmann W, Kellnberger S, Reinhardt S, et al. Ionoacoustic characterization of the proton Bragg peak with submillimeter accuracy[J]. Med Phys, 2015, 42(2): 567-574. DOI:10.1118/1.4905047 |
| [9] |
Lehrack S, Assmann W, Bertrand D, et al. Submillimeter ionoacoustic range determination for protons in water at a clinical synchrocyclotron[J]. Phys Med Biol, 2017, 62(17): L20-L30. DOI:10.1088/1361-6560/aa81f8 |
| [10] |
Sulak L, Armstrong T, Baranger H, et al. Experimental studies of the acoustic signature of proton beams traversing fluid media[J]. Nucl Instrum Meth, 1979(161): 203-217. DOI:10.1109/TNS.1978.4329325 |
| [11] |
Kipergil EA, Erkol H, Kaya S, et al. An analysis of beam parameters on proton-acoustic waves through an analytic approach[J]. Phys Med Biol, 2017, 62(12): 4694-4710. DOI:10.1088/1361-6560/aa642c |
| [12] |
Yoshinori H, Junichiro T, Sc NAB, et al. Acoustic pulse generated in a patient during treatment by pulsed proton radiation beam[J]. Radiat Oncol Invest, 1995, 3(1): 42-45. DOI:10.1002/roi.2970030107 |
| [13] |
Jones KC, Witztum A, Sehgal CM, et al. Proton beam characterization by proton-induced acoustic emission:simulation studies[J]. Phys Med Biol, 2014, 59(21): 6549-6563. DOI:10.1088/0031-9155/59/21/6549 |
| [14] |
Cox BT, Kara S, Arridge SR, et al. k-space propagation models for acoustically heterogeneous media:application to biomedical photoacoustics[J]. J Acoust Soc Am, 2007, 121(6): 3453-3464. DOI:10.1121/1.2717409 |
 2019, Vol. 39
2019, Vol. 39


