基于经验学习的智慧计划设计方法通过对大量先验计划进行智能学习,在此基础上构建质优计划的剂量学特性与患者个体化特性之间的关联模型[1-3],继而将该关联模型应用于新患者计划优化前的剂量学目标预测,有望实现计划设计的快速优化引导和个体化质量控制,进而有效提高临床计划的设计效率、同质化程度[4-6]。当前研究工作多以预测计划的剂量体积直方图(DVH)或剂量学指征项为主,然而这些均为累积型数据,将其作为优化目标不利于实现对感兴趣区内剂量的体素级精细调整,使求解空间受限,从而更高概率地产生次优甚至不可行计划解[7-8]。以三维剂量分布为预测对象,并将其作为优化引导是解决上述问题的理想方案。本团队前期以危及器官(organs at risk,OARs)体素为研究对象,采用神经网络方法并结合对射线角度、器官体积和器官间空间位置关系等影响因素的充分考虑,成功地构建了OARs的三维剂量分布预测模型[9]。但预测具有不确定性,该不确定性会对后续优化引导产生较大影响。因此,本研究在前期工作的基础上,提出一种可充分利用预测剂量分布信息,同时最大限度地改善输出计划质量的调强放疗计划优化方法,该方法以预测剂量分布作为优化引导,使优化输出计划质量逼近预测水平,并同时耦合等效均匀剂量优化目标,在预测引导的基础上扩大优化求解空间,从而进一步改善计划质量。
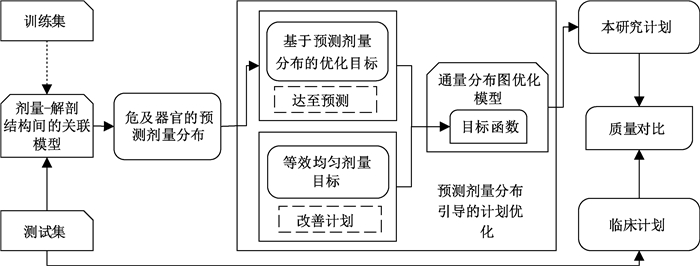
材料与方法1.优化方法的实现框架:如图 1所示,首先通过剂量-解剖结构关联模型得出OAR三维剂量分布预测;利用该预测剂量分布构建基于体素的优化目标函数,最小化OAR内体素的计算剂量与其对应预测剂量间的平方差累加值,使输出计划的质量趋于预测水平,同时添加OAR的等效均匀剂量目标进一步改善优化的求解空间。方法的有效性利用8例宫颈癌IMRT计划进行验证,比较方法所得计划质量与原始计划间的差异。
|
图 1 提出的基于预测剂量分布和gEUD混合目标的优化方法研究框架 Figure 1 Framework of proposed predicted 3D dose and gEUD based optimization method |
2.试验数据:选取8例临床优质宫颈癌IMRT计划,靶区仅有PTV,处方剂量均为45 Gy,采用分次治疗:1次/d,1.8 Gy/次,5~5.5/周。所有计划均由资深物理师在临床规范引导下,利用Eclipse计划系统(Varian Medical Systems,Palo Alto,美国Varian公司)完成,并通过美国Varian公司的6 MV光子直线加速器执行,行7野(150°、100°、50°、0°、310°、260°、210°)等间距共面照射。计划涉及的危及器官集中,直肠与膀胱与靶区重叠区域较大(分别位于肿瘤后位与直肠前位,肿瘤前位与膀胱后位),在IMRT中较受重视,因而被作为本研究的关注对象。
3.三维剂量分布预测:具体见参考文献[9],预测模型以OAR体素的剂量为输出特征,输入特征为体素到PTV边缘、PTV几何中心以及其他OARs边缘的距离、体素对于PTV几何中心的三维角度和PTV体积等,训练方法为前馈反向传播神经网络。直肠和膀胱的预测剂量分布的相对均方根误差分别为2.60%和2.98%。
4.优化模型的建立:利用危及器官的三维剂量分布预测构建基于体素的优化目标函数,以此作为优化引导,同时添加危及器官的等效均匀剂量目标函数以最大限度地降低OAR受量,此外,也设置约束项保证靶区内部剂量覆盖率和均匀性,并令靶区周围指定距离内的组织服从一定的剂量跌落规则,将各目标函数加权从而构成新的优化模型,优化以光子强度通量图x作为求解对象,最小化4项子目标的加权总二次损失函数F,同时添加实际条件约束限制C。其中目标函数第1项f优化危及器官剂量分布使其趋近于预测剂量分布;第2项gEUD无限制降低OAR剂量;第3项g优化靶区内剂量使其趋近于处方剂量;第4项h则优化靶区周围组织剂量使其满足特定跌落规则。新的优化模型数学表达式为:
| $ \begin{array}{l} MinF(x) = \sum\limits_i^{{\rm{ NOARs }}} {\left\{ {{w_i}f\left[ {{d_i}(x), d_i^{{\rm{ Pred}}{\rm{. }}}} \right]} \right.} + w_i^{{\rm{gEUD}}}{\mathop{\rm gEUD}\nolimits} \left[ {{d_i}(x)} \right]\} + \\ \sum\limits_j^{{\rm{NPTVs}}} {{w_j}} g\left[ {{d_j}(x), {{\hat d}_j}} \right] + {w^{NT}}h\left[ {d(x), {d^{NT}}} \right]\\ S.t.\quad C[d(x)] \le 0, x \ge 0 \end{array} $ | (1) |
式中,NOARs、NPTVs分别为危及器官、靶区的数目;NT为PTV边缘外扩1 cm的环,记为(PTV+1 cm)-PTV;f为预测剂量分布优化目标函数;gEUD为等效均匀剂量目标函数;g为临床上常用的均匀处方剂量目标函数,处方剂量用
(1) 利用预测剂量分布作为优化引导:以重现所预测的三维剂量分布为预测引导计划优化的最直观解决方案,最小化计算剂量分布与预测剂量分布之间的点对点差异,对感兴趣区内剂量进行空间雕刻。对应的预测剂量分布优化目标函数表达式为:
| $ f\left(d, d^{\text { Pred. }}\right)=\int_{0}^{1} \max \left\{d(v)-d^{\text { Pred. }}(v), 0\right\}^{2} \mathrm{d} v $ | (2) |
式中,v为百分比体积,该目标仅惩罚计算剂量在劣于预测剂量时,与其之间的差异。
(2) 耦合gEUD目标以弥补预测不确定性:仅以预测作为目标引导优化的方法具有一定的局限性,一是预测本身存在固有误差,其引导的优化结果会保留该误差信息;二是优化在当前计划质量达到预测后便会停止,未有进一步的探索。本方法则在预测引导目标的基础上,耦合了OAR的gEUD目标[14],该目标的梯度始终非负,意味着可无限制地降低OAR剂量,从而最大限度地提升计划质量,弥补预测局限性对优化造成的影响。其函数表达式为:
| $ \operatorname{gEUD}(d)=\left\{\left(\int_{0}^{1} d^{\alpha}(v) \mathrm{d} v\right)^{1 / \alpha}\right\}^{2} $ | (3) |
式中,α为生物特性参数,本研究中直肠和膀胱的α均设为2,旨在减少其区域内的高剂量体积以及减低其平均剂量[15]。
5.试验参数:因预测剂量分布保留了器官间的权衡信息,将其作为引导可降低优化目标权重选择的敏感度,所以本优化方法中无需复杂的权重调整过程,模型中OARs的f的权重均设为1,gEUD、g和h的权重分别为6×10-4、0.5和0.2。预设的靶区以及周围照射区域的剂量约束有:PTV的D99%≥43.2 Gy、D97%≥44 Gy、V99%≥94%、D1%≤49 Gy、D10%≤48 Gy、Dmax≤51 Gy、(PTV+1 cm)-PTV的Dmax≤50 Gy。优化使用序列二次规划算法求解,最大迭代次数为120,均在Windows 7(Intel 3.4Ghz 4核CPU)操作系统下Matlab2016b平台上实现,结果统一按照原始计划中PTV的99%处方剂量覆盖体积进行归一化。
6.统计学处理:应用SPSS 22.0软件进行数据分析。经检验相关数据分布符合正态分布,数据以x±s表示,不同计划的指征项差异采用配对样本t检验进行评估。P < 0.05为差异有统计学意义。
结果1.优化方法的求解情况:该优化方法具有可行解,优化在第100~108次迭代时即可收敛,耗时40~50 min。单次优化即可完成求解,且仅涉及几个固定参数,一旦确定后则无需二次的人工干预。
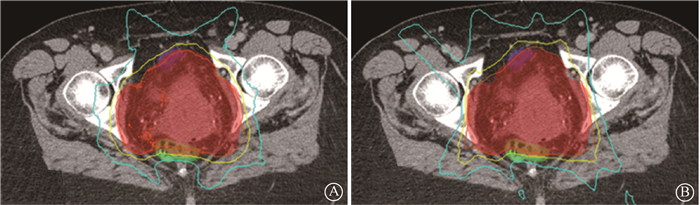
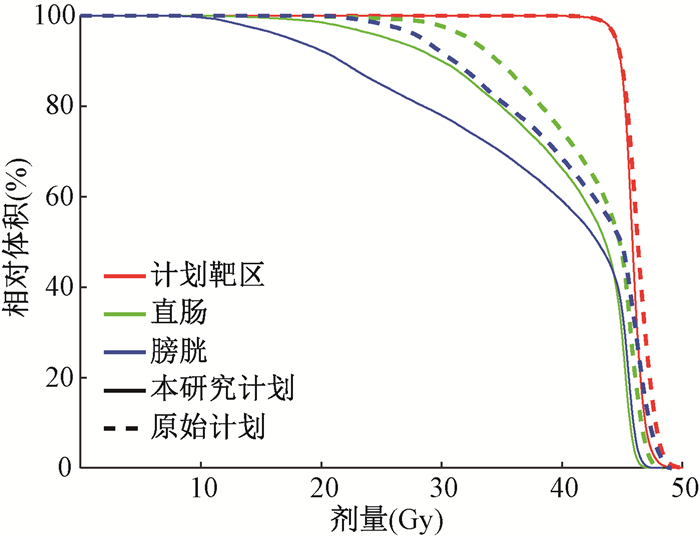
2.本研究计划和原始计划的质量比较:从第3例患者的剂量分布(图 2)上可知,本研究优化计划相比于原始计划,其剂量分布更加适形,PTV与OARs的重叠区域剂量更低,直肠与膀胱内的40 Gy和45 Gy剂量线均更优;从各感兴趣区的DVH曲线上(图 3)看,本研究计划的靶区DVH更为陡峭,直肠、膀胱的DVH也均更优。此外,从全8例患者的平均指征项(表 1)上看,本研究计划的靶区质量更优,其D1%和D10%分别减小了(0.37±0.67)Gy和(0.38±0.62)Gy;OARs剂量也均得到了降低,直肠的V30和V45分别减小了(6.60±3.53)%和(17.03±7.44)%(t=-4.954、-6.055,P < 0.05)。膀胱的V30和V45分别减小了(14.74±5.61)%和(14.99±4.53)%(t=-6.945、-8.759,P < 0.05)。本优化方法可保证靶区剂量覆盖率,提高其剂量均匀性,减少剂量热点,同时降低危及器官的受照剂量。
|
A.本研究计划;B.原始计划 图 2 第3例宫颈癌患者不同计划的计划靶区(红色阴影)、直肠(绿色阴影)和膀胱(蓝色阴影)的横截面剂量分布比较 A. Proposed plan; B. Original plan Figure 2 Transversal dose distribution comparisons of PTV (red shaded), rectum (green shaded) and bladder (blue shaded) between different plans for cervical cancer case 3 |
|
图 3 第3例宫颈癌患者不同计划的靶区、直肠与膀胱DVH图比较 Figure 3 DVH comparisons of PTV, rectum and bladder between different plans for cervical cancer case 3 |
|
|
表 1 8例宫颈癌患者不同计划的平均剂量学指征项比较(x±s) Table 1 Average dosimetric endpoints comparisons for 8 cervical cancers(x±s) |
3.对gEUD目标所起作用的验证:为评估gEUD目标对优化的改善作用,实验也将上述优化计划与仅以预测作为目标引导所得优化计划(仅预测引导计划)进行了比较。以第5例患者为例,首先从仅预测引导所得计划与预测计划的DVH曲线以及指征项的对比(图 4)中可知,本研究中以预测为引导的优化模型可保证输出计划质量不差于预测水平:直肠与膀胱的DVH均有改善,相关指征项均有不同程度的降低;并也在此基础上评估gEUD目标对后续优化的促进作用,从本研究计划与仅以预测为引导的优化计划的对比结果(图 4)中可知,耦合gEUD目标可在预测引导优化的基础上进一步提升计划质量,直肠、膀胱的整体受量均得到降低,其中直肠的V30和V45分别减少了1.65%和2.75%,膀胱的V30和V45分别减少了5.58%和1.28%,但靶区质量未有损失。

|
注:5B中横坐标1~10分别代表PTV的D99%、D97%、D1%、D10%,直肠的V30、V45、Dmax以及膀胱的V30、V45、Dmax 图 4 第5例宫颈癌患者不同计划质量间的比较 A. DVH;B.剂量学指征项 Figure 4 Plan quality comparison among different plans for cervical cancer case 5 A. DVH; B. Dosimetric endpoints |
讨论
本研究在团队成功构建的危及器官三维剂量分布预测模型的基础上,提出了一种基于预测三维剂量分布与gEUD混合优化目标的调强放疗计划优化方法,该方法利用预测剂量分布作为优化引导,可保证输出计划质量至少不差于预测,并同时耦合危及器官的gEUD目标,以此无限制地降低OAR受量,从而进一步改善计划质量。方法的有效性通过8例宫颈癌IMRT计划进行验证,结果证明该方法具有可行解且收敛快速,同时可保证输出计划的质优性。
当前基于经验学习的计划设计研究的重点在于构建更加准确的预测剂量分布模型,而对该预测的临床应用方案鲜有提及,一般将其作为调整计划等剂量线时的参照信息;或以重现预测剂量为求解策略,将其引入至目标函数中以进行计划优化[16-17],该种方法虽可得出可行计划,但在一定程度上限制了最优化求解的空间,其所得计划质量往往仅是接近于预测或原始计划,与其间差异未有统计学意义。本研究方法中将预测剂量分布目标与gEUD目标进行耦合,实现了两者的优势互补,前者可对体素剂量的空间分布进行精确的控制,后者则可弥补前者作为优化引导时提供优化空间有限的缺陷。
本研究方法虽可在预测目标过于宽松时,利用gEUD对危及器官质量进行补偿以保证计划质量,但在预测过于严格时,则需通过重新调整目标权重因子以完成优化。Ahmed等[18]在不需要任何先验信息的情况下构建了危及器官的DVH曲线集,并依据DVH被实现的可行性程度对这些DVH进行了分级,可将其作为参考信息,利用该信息对预测进行预处理或是根据预测所处的可行度级别对其目标选择合适的权重参数。此外,本研究应用的预测剂量目标函数要求所有体素剂量不可劣于其对应的预测值,该目标要求可能较为严格,今后将尝试对预测剂量的位置信息进行松弛,以构建更具包容性的应用目标函数。
本研究方法中,原始计划数据直接影响到预测模型的准确性以及后续引导优化的计划质量,由于实验数据均仅来源于本团队的合作单位,所得研究结果可能不具备临床代表性,但本研究的优化策略值得推广,接下来将收集来自不同单位或是更多分期以及病种的计划数据,以对本方法的临床可行性做进一步的验证。
综上所述,本研究成功提出了一种基于预测三维剂量分布和gEUD混合优化目标的调强放疗计划优化新方法,该方法可有效利用预测剂量分布信息的同时保障输出计划的优质性。
利益冲突 无作者贡献声明 贾启源负责研究的设计、实施以及论文的撰写、修改;郭芙彤、吴艾茜、亓孟科、麦燕华、孔繁图负责数据的收集、统计和分析;周凌宏、宋婷负责研究设计、技术指导和论文修改
| [1] |
Wu B, Ricchetti F, Sanguineti G, et al. Patient geometry-driven information retrieval for IMRT treatment plan quality control[J]. Med Phys, 2009, 36(12): 5497-5505. DOI:10.1118/1.3253464 |
| [2] |
Appenzoller LM, Michalski JM, Thorstad WL, et al. Predicting dose-volume histograms for organs-at-risk in IMRT planning[J]. Med Phys, 2012, 39(12): 7446-61. DOI:10.1118/1.4761864 |
| [3] |
Song T, Staub D, Chen M, et al. Patient-specific dosimetric endpoints-based treatment plan quality control in radiotherapy[J]. Phys Med Biol, 2015, 60(21): 8213. DOI:10.1088/0031-9155/60/21/8213 |
| [4] |
Wu B, Ricchetti F, Sanguineti G, et al. Data-driven approach to generating achievable dose-volume histogram objectives in intensity-modulated radiotherapy planning[J]. Int J Radiat Oncol Biol Phys, 2011, 79(4): 1241-1247. DOI:10.1016/j.ijrobp.2010.05.026 |
| [5] |
Li N, Carmona R, Sirak I, et al. Highly efficient training, refinement, and validation of a knowledge-based planning quality-control system for radiation therapy clinical trials[J]. Int J Radiat Oncol Biol Phys, 2016, 97(1): 164. DOI:10.1016/j.ijrobp.2016.10.005 |
| [6] |
Song T, Li N, Zarepisheh M, et al. An automated treatment plan quality control tool for intensity-modulated radiation therapy using a voxel-weighting factor-based re-optimization algorithm[J]. PLoS One, 2016, 11(3): e0149273. DOI:10.1371/journal.pone.0149273 |
| [7] |
Zarepisheh M, Uribe-Sanchez AF, Li N, et al. A multicriteria framework with voxel-dependent parameters for radiotherapy treatment plan optimization[J]. Med Phys, 2014, 41(4): 041705. DOI:10.1118/1.4866886 |
| [8] |
Wilkens JJ, Alaly JR, Zakarian K, et al. IMRT treatment planning based on prioritizing prescription goals[J]. Phys Med Biol, 2007, 52(6): 1675-92. DOI:10.1088/0031-9155/52/6/009 |
| [9] |
孔繁图, 麦燕华, 亓孟科, 等. 基于神经网络学习方法的放疗计划三维剂量分布预测[J]. 南方医科大学学报, 2018, 38(6): 683-690. Kong FT, Mai YH, Qi MK, et al. Prediction of three-dimensional dose distribution in intensity-modulated radiation therapy based on neural network learning[J]. J South Med Univ, 2018, 38(6): 683-690. DOI:10.3969/j.issn.1673-4254.2018.06.07 |
| [10] |
Bokrantz R. Multicriteria optimization for volumetric-modulated arc therapy by decomposition into a fluence-based relaxation and a segment weight-based restriction[J]. Med Phys, 2012, 39(11): 6712. DOI:10.1118/1.4754652 |
| [11] |
Fredriksson A, Bokrantz R. A critical evaluation of worst case optimization methods for robust intensity-modulated proton therapy planning[J]. Med Phys, 2014, 41(8): 081701. DOI:10.1118/1.4883837 |
| [12] |
Scherrer A, Yaneva F, Grebe T. A new mathematical approach for handling DVH criteria in IMRT planning[J]. J Global Optim, 2015, 61(3): 407-428. DOI:10.1007/s10898-014-0202-2 |
| [13] |
Deasy JO, Blanco AI, Clark VH. CERR:a computational environment for radiotherapy research[J]. Med Phys, 2003, 30(5): 979-985. DOI:10.1118/1.1568978 |
| [14] |
Wu Q, Mohan R, Niemierko A, et al. Optimization of intensity-modulated radiotherapy plans based on the equivalent uniform dose[J]. Int J Radiat Oncol Biol Phys, 2002, 52(1): 224-235. DOI:10.1016/S0360-3016(01)02585-8 |
| [15] |
Craft D. A guide to using multi-criteria optimization (MCO) for IMRT planning in Raystation[Z]. Boston: Massachusetts General Hospital, 2011.
|
| [16] |
Mcintosh C, Welch M, Mcniven A, et al. Fully automated treatment planning for head and neck radiotherapy using a voxel-based dose prediction and dose mimicking method[J]. Phys Med Biol, 2017, 62(15): 5926-5944. DOI:10.1088/1361-6560/aa71f8 |
| [17] |
Fan J, Wang J, Chen Z, et al. Automatic treatment planning based on three-dimensional dose distribution predicted from deep learning technique[J]. Med Phys, 2018, 45(1): 370-381. DOI:10.1002/mp.13271 |
| [18] |
Ahmed S, Nelms B, Gintz D, et al. A method for a priori estimation of best feasible DVH for organs-at-risk:Validation for head and neck VMAT planning[J]. Med Phys, 2017, 44(10): 5486-5497. DOI:10.1002/mp.12500 |
 2019, Vol. 39
2019, Vol. 39


