2. 清华大学核能与新能源技术研究院, 北京 100084
2. Institute of Nuclear and New Energy Technology, Tsinghua University, Beijing 100084, China
2011年3月11日发生的日本福岛核事故向环境释放了大量放射性物质,对公众与环境造成了不可忽视的辐射影响[1-2]。福岛核事故放射性释放源项,是福岛核事故向环境释放放射性物质的核素种类和放射性活度的描述。然而,由于福岛核事故的反应堆状态参数不完整,难以采用根据工况计算放射性释放源项的方法估计源项。到目前为止,国际上对福岛核事故释放源项的相关研究仍在进行。
基于数据同化的核事故源项反演可利用事故期间辐射环境监测数据估计释放源项,在福岛核事故后得到国内外的广泛重视。变分数据同化法(variational data assimilation,VAR)[3]与截断总体最小二乘法(truncated total least squares,TTLS)[4]有效结合后形成的截断总体最小二乘变分核事故源项反演模型(TTLS-VAR)[5-6],不仅保留了VAR的有效平衡利用所研究时空范围内全部监测数据的优点,而且能考虑扩散模型的误差,在反演问题不适定时合理平滑结果。
本研究使用TTLS-VAR模型对福岛核事故中137Cs释放源项进行估计,并与国际公开结果相对比,分析并讨论估计结果的准确性。
材料与方法1.源项估计方案:本研究对福岛核事故137Cs释放率时间序列进行估计。研究时段总长为20 d,由2011年3月11日0时起,至2011年3月31日0时止,研究区域覆盖了日本本州岛的大部分地区。研究中采用的原始气象资料来自欧洲中尺度天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF),再通过美国天气预报模式(weather research and forecasting,WRF)插值模拟,获得足够精细的气象场。为了与气象场的网格分布相一致,具体研究区域为137.53°E至143.53°E,34.72°N至40.72°N(图 1)。水平网格间距为0.05°,水平网格数120×120,垂直层数为15层,范围从0~ 8 km。释放发生在第一层(中间高度为20 m)与第二层(中间高度为80 m),释放比例为1:2,由核岛厂房高度和事故分析大致确定,被法国国立路桥学校大气环境研究中心(CEREA)推荐采用。若不作特别说明,本研究中所有时间皆为格林尼治标准时间。
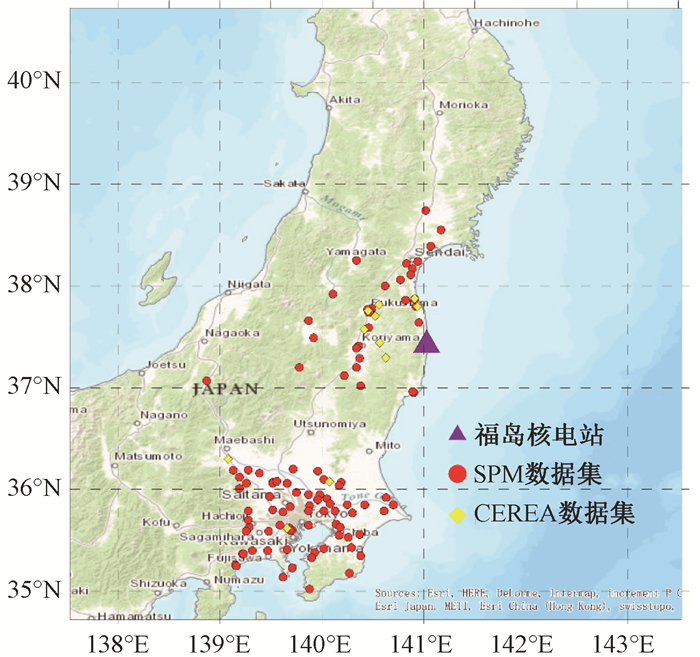
|
图 1 研究范围与监测点分布 Figure 1 Research range and monitoring point distribution |
2.监测数据:本研究同时使用两套监测数据进行137Cs释放源项的反演计算。其中,一套监测数据来源于日本原子能机构(JAEA)对日本各省空气悬浮颗粒物(suspended particulate matters,SPM)样品进行的137Cs逐时空气活度浓度测量[7-9](简称为SPM数据集);另一套为CEREA对福岛核事故放射性释放源项研究时使用的日本本土137Cs空气活度浓度[10-11](简称为CEREA数据集,由CEREA提供)。这两个数据集的监测点均分布在福岛核电站大中尺度范围内,如图 1所示。
SPM数据集于2014年起应用于福岛核事故的放射性物质大气扩散研究与事故后评价,共有99个监测点,采样时间多集中于3月12日16时至16日15时和3月19日16时至23日15时,但分布不均匀。SPM数据集共有有效监测数据13 939个,其中7 491个数据低于探测下限,计算中设为0。
CEREA数据集中共有监测数据104个,其中95个数据的采样时间在研究时段内,分布同样不均匀,其他数据采样时间位于3月31日0时至4月4日0时。由于放射性物质从释放至被监测到之间存在时间间隔,在源项估计中将扩散模拟时段延长至2011年4月4日0时,以尽量利用监测数据信息。CEREA数据集中不包含低于探测下限的数据。
3. TTLS-VAR源项反演模型:本研究所使用的源项反演模型TTLS-VAR由本研究组提出并建立[5-6],基于CEREA核事故变分源项反演模型VAR[10-12]改进而来。TTLS-VAR模型不受监测时间与频率的限制,能综合研究时空范围内的全部监测数据,并能考虑扩散模型与监测数据的误差,以提高源项估计的准确性。此外,由于气象数据及扩散模型等存在误差,且监测数据的分布不一定均匀,核事故源项反演问题常常是不适定的。TTLS可以在反演问题不适定时有效平滑估计结果,改善结果的震荡性[4]。
设位置l上t时刻的释放率为σl, t,其背景估计为σ(l, t)b。于是,对研究区域L上时段T内,有释放源项向量σ=(σ1, 1…σl, t…σL, T)T和其背景场σb=(σ(1, 1)b…σ(l, t)b…σ(L, T)b)T。
设T内共有监测数据I个,第i个监测数据为yi。同理,有监测向量y=(y1…yi…yI)T。
TTLS-VAR模型中,σ的求解是靠代价函数最小化实现的。设σ与y均符合高斯分布,其中各元素互不相关,σb保守设为0向量,Hσ为扩散模型模拟数据,H为扩散过程对释放源项的雅可比矩阵,即扩散模型算子,TTLS-VAR模型的代价函数为:
| $ J = \frac{1}{2}\left( {{{\left\| {y_k^{\rm{c}} - H_k^c\sigma } \right\|}^2}} \right) + \frac{1}{2}\left( {{{\left\| \sigma \right\|}^2}{{\left( m \right)}^{ - 2}}} \right) $ | (1) |
式中,
本研究采用L-curve法[13-14]求解正则化参数。确定k时,需要将可能范围内的所有值逐一作为k,计算
本研究采用拟牛顿法(Quasi-Newton methods)中的LBFGS(Limited-memory Broyden-Fletcher-Goldfarb-Shanno)[15]实现代价函数的最小化,求解福岛核事故137Cs释放源项。
4.扩散模型与相关参数:本研究使用CEREA开源平台Polyphemus中的Polair 3D欧拉大气扩散模型[16-18]来计算TTLS-VAR中的扩散模型算子,原因有3点:为开源软件,易于获取与使用;大气扩散模拟质量良好,应用广泛,适用于本研究的模拟尺度;具备一定放射性核素大气扩散模拟的能力,且曾被多次用于切尔诺贝利与福岛核事故的源项反演研究[10-12]。
作为一种典型的欧拉大气扩散模型,Polair 3D以气态污染物连续性方程来描述污染物的释放、扩散、沉积及化学变化。在某一时刻的某个网格内,该方程的数学表达式为:
| $ \frac{{\partial C}}{{\partial t}} = div\left( {UC} \right) = div\left[ {\rho K\nabla \left( {\frac{C}{\rho }} \right)} \right] - {\mathit{\Lambda }^{\rm{s}}}C - {\mathit{\Lambda }^{\rm{d}}}C + \sigma $ | (2) |
式中,C为污染物浓度,Bq/m3; t为时间,s; U为三维风场矢量,m/s; ρ为空气密度,kg/m3; K为水平与垂直扩散参数组成的对角阵,m2/s; Λs为湿沉积因子,1/s; Λd为衰变系数,1/s; σ为该污染物的释放率, Bq-1·m3·s-1。
Polair 3D中的边界条件分为扩散边界与对流边界,扩散边界条件有:
(1) 在本研究的三维扩散区域中,区域的上边界(顶面)与侧向边界(4个侧面)上,设通量为0,表示为:
| $ K\nabla C \cdot n = 0 $ | (3) |
式中,n为计算区域内的单位法向量, m/s。
(2) 地面边界(底面)上,设垂直风速为0,考虑干沉积过程:
| $ K\nabla C \cdot n = - {v_{{\rm{dep}}}}C $ | (4) |
式中,vdep为干沉积速率, m/s。
对流边界条件中,入口边界为大气中原有污染物与释放污染物的对流入口,入口边界通量设为待计算污染物的全球大气输运模拟结果或某一指定值。由于此处的研究对象为137Cs气溶胶,其在全球大气环境中含量很低,故设入口边界通量为0。表达式为:
| $ n \cdot UC = 0 $ | (5) |
由上述Polair 3D方程与边界条件所示,若湍流扩散过程[式(2)中右式第1项]与湿沉积过程[式(2)中右式第2项]均为线性,并且干沉积过程也为线性,该扩散过程即为线性的。
本研究沿用了CEREA福岛核事故源项反演中的相关参数设置[10-11]。水平扩散参数设为固定值25 000 m2/s,垂直扩散参数由Louis参数化模型[19]确定,使湍流扩散过程为线性。陆地与水面上的干沉积速率固定值分别为1.50×10-3与1.00×10-4 m/s,云层中的湿沉积因子由Roselle-Binkowski模型[20]计算,而云层下的湿沉积因子则使用Maryon参数[21]计算,使沉积过程与137Cs气溶胶直径无关,也为线性。因此,扩散模型算子可以简单地用137Cs单位源项分段释放模拟计算得到[5]。计算步骤为:
(1) 设位置l上t时刻的137Cs单位释放序列为σl, td=(0…0 1 0…0)T,即,除位置l上t时刻的释放率为1 Bq/s,其余释放率均为0。
(2) 将σl, td作为释放源项代入扩散模型中,可取得所有监测点上各监测时间的浓度hl, t=(h(l, t), 1…h(l, t), i…h(l, t), I)T。
(3) 对各段单位释放率重复步骤(1)、(2),可以组合得到扩散模型算子H=(h1, 1…hl, t…hL, T)。
扩散模型算子的有效性可以通过比较算子和源项的乘积与Polair 3D对监测点位上的模拟结果来进行,如这两者近似相等,则算子有效。
5.源项估计结果对比资料:本研究利用IAEA公布的福岛核事故137Cs释放总量范围(7.0×1015~ 2.0×1016 Bq)[1]、联合国原子辐射效应科学委员会(UNSCEAR)公布137Cs释放总量范围(6.0×1015~ 2.0×1016 Bq)[2]和JAEA于2015年发表的福岛核事故137Cs释放序列[22](以下简称JAEA-2015),综合东京电力公司(TOEPC)2012年5月发布的福岛核电站事故调查报告[22-23]等文献中压力下降、氢气爆炸、建筑物释放等参考事故事件的起始时刻及持续时段,如表 1所示,对比并评价137Cs源项估计结果。
|
|
表 1 福岛核事故参考事件表 Table 1 Reference events in Fukushima nuclear accident |
表 1中U1、U2、U3分别表示福岛第一核电站1号、2号与3号机组。需要说明的是,JAEA-2015计算时已经考虑了表 1中所列重要参考事件的起始及持续时间[22],所以JAEA-2015的释放率曲线与参考事故事件较为符合。但由于计算方法的主观性太强,并对释放时间序列采取了平均化处理,JAEA-2015只是日本方面给出的最新结果,而不能看作是标准结果。
结果1.扩散模型算子有效性验证:以JAEA-2015作为源项,计算Polair 3D在监测点位上的模拟结果以及扩散模型算子与源项的乘积,一阶线性拟合结果如图 2所示。可以看出,模拟结果与算子计算结果相当接近,一阶线性拟合的系数为1.001,拟合优度(R2)为1.000,均方根误差(root mean squared error,RMSE)为0.089,说明本研究中算子与源项的乘积和Polair 3D模拟结果近似相等,扩散模型算子有效,小量的误差可能来自于网格浓度到监测点浓度的插值计算。
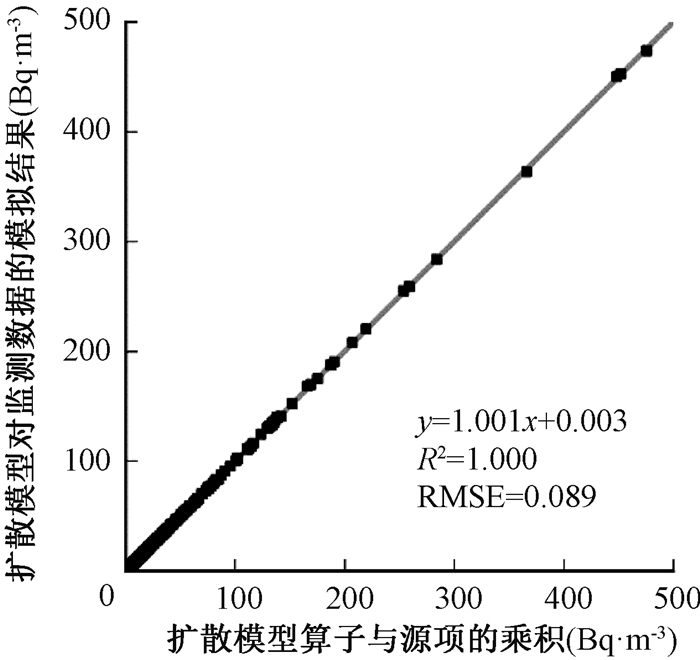
|
图 2 模拟结果与算子计算结果的线性拟合 Figure 2 Linear fitting of simulation and operator calculation |
2.正则化参数计算结果:如图 3所示,TTLS-VAR模型对正则化参数k的L-curve双对数曲线虽然为明显的“L”形状,但各点间的离散度较大。本研究选择曲线上两处较明显的拐点,取k值为100与192,分别计算正则化参数m并开展137Cs源项估计。k取100时,TTLS已经能使估计结果足够平滑,正则化参数m可取为极大值(本实验中取为1.00×1013 Bq/s)。k取192时,TTLS对结果的平滑处理不足,正则化参数m取为6.60×109 Bq/s,以加强估计结果的平滑度。
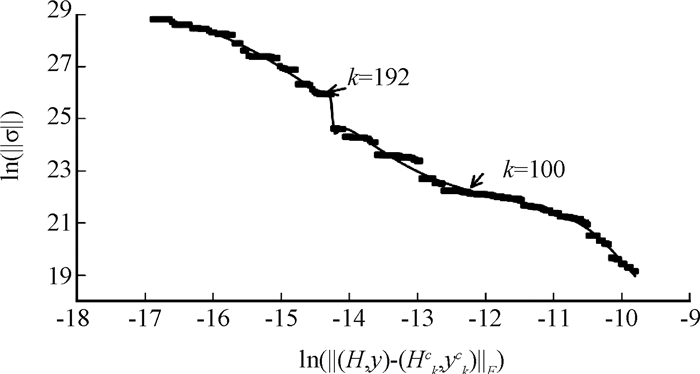
|
图 3 TTLS-VAR模型正则化参数k的L-curve双对数曲线 Figure 3 L-curve log-log plot of regularization parameter k of the TTLS-VAR |
3.源项估计结果:如图 4所示,k取100时TTLS-VAR模型对福岛核事故137Cs释放总量的估计结果为3.73×1016 Bq,超出IAEA与UNSCEAR参考范围区间范围约1.73×1016 Bq;而当k取192时,TTLS-VAR模型的估计结果为1.74×1016 Bq,在参考范围区间范围内,但更接近上界。本研究估计的137Cs释放总量较大应与SPM数据集中存在之前未考虑到的较高监测值有关。在SPM数据集中,福岛核电站北部最近的监测点为Haramachi,距福岛核电站约48 km。3月18日上午,福岛地区主风向偏西,放射性污染物向东面的太平洋方向扩散,而此时Haramachi监测到500 Bq/m3左右的气载137Cs,与3月18日早上的释放高峰相对应。从释放率曲线上看,k取100和192时,TTLS-VAR模型对释放率峰值位置的估计大致是相似的。其中,3月12日0时至15日21时以及18日0时至23日9时期间,各参考事故事件附近都出现了对应的释放峰位,并且释放率曲线的总体高低起伏趋势与JAEA-2015相似。3月18日至19日的释放高峰,亦与3号机组的泄漏事件相对应(表 1)。这些现象说明,TTLS-VAR模型的估计结果与目前已知的福岛核事故进程相符合。3月16日0时至18日0时以及23日15时至31日0时之间,释放率估计结果在背景场(0向量)附近。这是由监测数据大段缺失所致,与模型的反演质量无关。
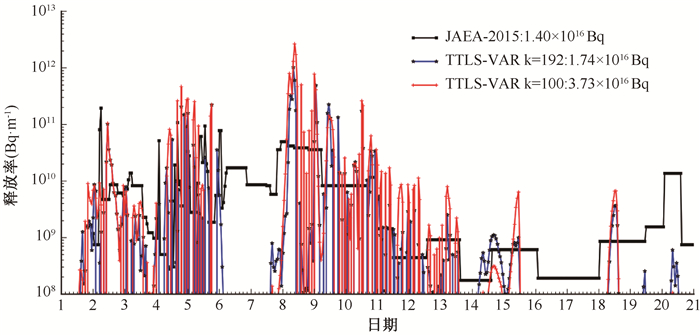
|
图中横坐标1,2,……,21表示3月11日至3月31日 图 4 137Cs估计释放率曲线与释放总量 Figure 4 Estimated 137Cs release rates and total amount |
与k取100相比,k取192时模型所估计的释放总量较小,释放率峰值较低,且在多数时间段上释放率曲线的震荡性有所减轻。这一现象说明,k值偏大且叠加Tikhonov正则化会增加估计结果的平滑度。
但是,在3月19日,k取100时模型估计结果的上下震荡幅度较小,且在3月14、15与19日上,其释放峰较k取192时连续。同时,k取100时的估计结果在3月15、17、24、29与30日出现释放峰少于k取192的情况。上述现象均说明,k取100时TTLS-VAR模型对扩散模型算子与监测向量修正的效果更加明显,而是否叠加Tikhonov正则化对估计结果的平滑效果在局部上不具有可比性。
4.数据同化质量:用本研究计算所得福岛核事故137Cs释放源项,对监测数据进行重建。之后,将重建结果与监测数据相比较,评价源项反演过程中,监测信息被融合与处理的程度,即数据同化质量。为量化监测数据与其重建结果之间的总体统计误差,表 2分别列出了SPM与CEREA数据集与其重建结果的统计误差参数值,包括分数偏差(FB)、归一化均方误差(NMSE)、相关系数(correlation coefficient,R)、0.5~2倍监测值范围内的数据比例(FAC2)与0.1~10倍监测值范围内的数据比例(FAC10)[24]。以上参数被美国环境署推荐,常用于评价大气扩散等模拟过程的质量。
|
|
表 2 137Cs监测数据重建结果的统计误差参数值 Table 2 Statistical parameters of the reconstructed results from 137Cs observations |
可以看出,当k取100时,两个数据集的重建结果与监测数据基本一致,且统计误差参数值接近完美水平,说明扩散模型算子与监测向量的修正程度良好。而当k取192时,对SPM数据集与CEREA数据集的重建结果多在监测数据的0.1~10倍之间,相关系数约为0.8,且有一定的低估。该现象说明,当TTLS-VAR模型中k值偏大时,Tikhonov正则化对数据同化质量的影响很大,导致数据同化质量偏低。
讨论福岛核事故释放源项是事故评价、公众防护、环境保护的基础。本研究利用大中尺度范围内的137Cs空气活度浓度监测数据,采用截断总体最小二乘变分核事故源项反演模型TTLS-VAR,估计了福岛核事故中137Cs的释放源项。
研究结果显示,137Cs释放总量为1.74×1016~ 3.73×1016 Bq,与IAEA与UNSCEAR公布的范围相接近,由于所采用的监测数据集中存在之前未考虑的较高监测值,释放总量有所偏大;137Cs释放曲线与日本JAEA的事故源项与进程分析具有较好的一致性,释放率最高峰出现在2011年3月18日,释放率超过1.00×1012 Bq/s,与事故进程中福岛核电站3号机组的泄漏事件相对应。
当正则化参数k的取值较为合适时,TTLS-VAR模型对扩散模型算子与监测向量的修正良好,释放总量估计值较高,释放率曲线的连续性较好;而当k值偏大时,估计的释放率峰值位置在整体上没有明显变化,释放总量的估计值相对较低,震荡性较小,对福岛核事故源项反演的不适定有更好的处理效果,但数据同化质量偏低。
本研究对137Cs释放源项的估计结果,可作为福岛核事故评价、公众辐射防护和环境影响评价的计算依据。
由于扩散模型具有误差,且监测数据分布不均匀,核事故源项反演问题经常是不适定的。虽然TTLS-VAR模型具有正则化过程,能够在一定程度上平滑释放源项的估计结果。然而,福岛核事故137Cs释放源项反演结果显示,估计得到的释放率曲线仍然存在震荡性。未来,可以在释放源项和监测数据的先验分布、正则化参数计算方法等方面开展深入研究,不断改进源项反演模型,提高其可行性、可靠性与稳定性,为工程应用提供基础。
利益冲突 无作者贡献表明 刘蕴负责实施研究、分析数据与论文撰写;刘新建、李红、曲静原指导论文修改;方晟参与数据分析与论文审阅
| [1] |
International Atomic Energy Agency. Fukushima Daiichi Accident report by the director general[R]. Vienna: IAEA, 2015.
|
| [2] |
United Nations Scientific Committee on the Effect of Atomic Radiation. Developments since the 2013 UNSCAER report on the levels and effects of radiation exposure due to the nuclear accident following the great east-japan earthquake and tsunami[R]. New York: UNSCEAR, 2016.
|
| [3] |
Dimet FXL, Talagrand O. Variational algorithms for analysis and assimilation of meteorological observations:theoretical aspects[J]. Tellus A, 1986, 38(2): 97-110. DOI:10.3402/tellusa.v38i2.11706 |
| [4] |
Fierro RD, Golub GH, Hansen PC. Regularization by truncated total least squares[J]. Siam J Sci Comput, 1997, 18(4): 1223-1241. DOI:10.1137/S1064827594263837 |
| [5] |
刘蕴.基于变分数据同化的核事故源项反演模型研究[D].北京: 清华大学核能与新能源技术研究院, 2017. Liu Y. Research on source inversion for nuclear accidents based on variational data assimilation[D]. Beijing: Institute of Nuclear and New Energy Technology, Tsinghua University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10003-1018876077.htm |
| [6] |
刘蕴, 刘新建, 李红, 等. 截断总体最小二乘变分核事故源项反演数值研究[J]. 核动力工程, 2019, 39(1): 120-125. Liu Y, Liu XJ, Li H, et al. Numerical research on source inversion for nuclear accidents based on variational data assimilation coping with truncated total least squares[J]. Nucl Power Eng, 2019, 39(1): 120-125. DOI:10.13832/j.jnpe.2019.01.0120 |
| [7] |
Tsuruta H, Oura Y, Ebihara M, et al. First retrieval of hourly atmospheric radionuclides just after the Fukushima accident by analyzing filter-tapes of operational air pollution monitoring stations[J]. Sci Rep, 2014, 4(4): 6717. DOI:10.1038/srep06717 |
| [8] |
Oura Y, Ebihara M, Tsuruta H, et al. Determination of atmospheric radiocesium on filter tapes used at automated SPM monitoring stations for estimation of transport pathways of radionuclides from Fukushima Daiichi Nuclear Power Plant[J]. J Radioanal Nucl Chem, 2015, 303(2): 1555-1559. DOI:10.1007/s10967-014-3662-4 |
| [9] |
Oura Y, Ebihara M, Tsuruta H, et al. A database of hourly atmospheric concentrations of radiocesium (134Cs and 137Cs) in suspended particulate matter collected in March 2011 at 99 air pollution monitoring stations in Eastern Japan[J]. J Nucl Radiochem Sci, 2015, 15(2): 1-12. DOI:10.14494/jnrs.15.2_1 |
| [10] |
Winiarek V, Bocquet M, Saunier O, et al. Estimation of errors in the inverse modeling of accidental release of atmospheric pollutant:application to the reconstruction of the cesium-137 and iodine-131 source terms from the Fukushima Daiichi power plant[J]. J Geophys Res Atmos, 2012, 117(D18): 1-19. DOI:10.1029/2012jd018107 |
| [11] |
Winiarek V, Bocquet M, Duhanyan N, et al. Estimation of the caesium-137 source term from the Fukushima Daiichi nuclear power plant using a consistent joint assimilation of air concentration and deposition observations[J]. Atmos Environ, 2014, 82: 268-279. DOI:10.1016/j.atmosenv.2013.10.017 |
| [12] |
Davoine X, Bocquet M. Inverse modelling-based reconstruction of the Chernobyl source term available for long-range transport[J]. Atmos Chem Phys, 2007, 7(6): 1549-1564. DOI:10.5194/acp-7-1549-2007 |
| [13] |
Sima DM, Van Huffel S. Level choice in truncated total least squares[J]. Comput Stat Data An, 2007, 52(2): 1103-1118. DOI:10.1016/j.csda.2007.05.015 |
| [14] |
Hansen PC. Analysis of discrete ill-posed problems by means of the L-curve[J]. Siam Rev, 1992, 34(4): 561-580. DOI:10.1137/1034115 |
| [15] |
Zhu C, Byrd RH, Lu P, et al. Algorithm 778:L-BFGS-B:Fortran subroutines for large-scale bound-constrained optimization[J]. ACM T Math Software, 1997, 23(4): 550-560. DOI:10.1145/279232.279236 |
| [16] |
Boutahar J, Lacour S, Mallet V, et al. Development and validation of a fully modular platform for numerical modelling of air pollution:POLAIR[J]. Int J Environ Pollut, 2004, 22(1-2): 17-28. DOI:10.1504/ijep.2004.005474 |
| [17] |
Mallet V, Sportisse B. 3-D chemistry-transport model polair:numerical issues, validation and automatic-differentiation strategy[J]. Atmos Chem Phys Discuss, 2004, 4(2): 1371-1392. DOI:10.5194/acpd-4-1371-2004 |
| [18] |
Roustan Y, Sartelet KN, Tombette M, et al. Simulation of aerosols and gas-phase species over Europe with the POLYPHEMUS system. Part Ⅱ:Model sensitivity analysis for 2001[J]. Atmos Environ, 2010, 44(34): 4219-4229. DOI:10.1016/j.atmosenv.2010.07.005 |
| [19] |
Louis J-F. A parametric model of vertical eddy fluxes in the atmosphere[J]. Bound Lay Meteorol, 1979, 17(2): 187-202. DOI:10.1007/bf00117978 |
| [20] |
Roselle SJ, Binkowski FS. Science algorithms of the EPA Models-3 Community multiscale air quality (CMAQ) modeling system: Cloud dynamics and chemistry[R]. Washington DC: US EPA, 1999.
|
| [21] |
Maryon RH, Smith FB, Conway BJ, et al. The UK nuclear accident model[J]. Prog Nucl Energ, 1991, 26(2): 85-104. DOI:10.1016/0149-1970(91)90043-o |
| [22] |
Katata G, Chino M, Kobayashi T, et al. Detailed source term estimation of the atmospheric release for the Fukushima Daiichi Nuclear Power Station accident by coupling simulations of an atmospheric dispersion model with an improved deposition scheme and oceanic dispersion model[J]. Atmos Chem Phys, 2015, 15(2): 1029-1070. DOI:10.5194/acp-15-1029-2015 |
| [23] |
Tokyo Electric Power Company. Estimation of Radioactive material released to the atmosphere during the Fukushima Daiichi NPS accident[R]. Tokyo: TOEPC, 2012.
|
| [24] |
Hanna SR. Confidence limits for air quality model evaluations, as estimated by bootstrap and jackknife resampling methods[J]. Atmos Environ, 1989, 23(6): 1385-1398. DOI:10.1016/0004-6981(89)90161-3 |
 2019, Vol. 39
2019, Vol. 39


