双能X射线骨密度仪是目前最常用的骨质疏松诊断仪器^[1-2]，其原理是采用双能X射线吸收法(dual-energy X-ray absorptiometry，DXA)即高能和低能两种X射线穿过人体组织^[3]，根据不同能量X射线在不同组织中的衰减系数不同的特点，计算出骨骼的面密度(即单位投影面积的物体质量)并得到骨密度图像。近年来，随着基于DXA骨密度图像评估骨质疏松和骨折风险的新方法不断发展，对DXA成像质量的要求越来越高^[4-6]。然而制约DXA图像质量的一个重要因素是非最优化的成像参数。本研究构建了基于CT数据的体素模型，利用蒙特卡罗通用软件MCNPX^[7]模拟DXA腰椎成像过程，通过改变不同双能X射线管电压组合，添加不同厚度的过滤铜片以及不同入射粒子数比值，在尽可能低的剂量范围内，以期获得DXA腰椎成像的最优化参数。

1.蒙特卡罗方法模拟成像过程

(1) 体素模型的构建：选取1名77岁男性的CT数据，编写MATLAB脚本，读取CT的DICOM文件，获取HU值。采用Schneider方法对HU值进行划分^[8]；并根据HU值与物质密度的转换关系和HU值与材料组成的对应关系，计算出每个像素的密度与材料组成，将其分别归类到24种组织材料，每个材料都有其独有的元素组成和密度；按照像素在CT上的空间位置拼接每个体素，所有体素填充构成可用于模拟计算的体素模型^[9]。

(2) 蒙特卡罗模拟扫描过程：模拟骨密度仪电压切换法^[10]，由SpekCalc软件计算获得钨阳极X射线管能谱^[11-12]。光子从平面面源出射，沿着正位后前方向照射体素模型的腰椎区域^[13]，射野大小为10 cm×18 cm。照射区域的人体厚度约为22 cm，处于正常腰椎厚度范围内，可以忽略能谱硬化现象的影响^[14]。探测器分为200×360个理想探测单元，每个探测单元尺寸为0.5 mm×0.5 mm×15 cm。使用计数卡F4记录每个探测单元光子通量(光子强度，photons/cm²)和相对误差，使用计数卡F6记录整个体模吸收剂量，单位MeV/(g·photon)换算为μGy/photon。

2. DXA骨密度图像的计算：DXA骨密度计算公式^{[2, 15]}为：

式中，m_b为骨骼的面密度，g/cm²；I^L、I^H分别为低能和高能的透射线强度，I₀^L、I₀^H分别为低能和高能的入射线强度；τ_b^l、τ_b^h分别为低能和高能X射线在骨骼中的质量衰减系数，τ_s^l、τ_s^h分别为低能和高能X射线在软组织中的质量衰减系数，cm²/g；${R_{\rm{s}}} = \frac{{\tau _{\rm{s}}^l}}{{\tau _{\rm{s}}^h}}$，为脂肪与肌肉含量的测量值，须提前被定义以计算骨密度图像中每个像素点数值，通过扫描不含骨骼的软组织获得R_s^[15]。若m_b=0，R_s为：

式中，I_s^L、I_s^H分别为低能和高能X射线照射去除骨骼只存在软组织体模的透射线强度。双能X射线能谱分别照射完整体模、空气、去除骨骼的软组织体模，即双能能谱组合得到6幅投影图像，对应Iⁱ、I₀ⁱ、I_sⁱ，i=L, H。将这6幅图像的每个像素数据对应代入公式(2)和(1)中，其中不同能量X射线在骨骼中的质量衰减系数从NIST数据库中查表获得^[16]，在临床成像情况下，通过能谱的平均能量插值得到能谱质量衰减系数等效值，从而计算得到被照射区域的DXA骨密度图像，图中每个像素的数据值代表了该点的骨密度值。

3.骨密度图像噪声、吸收剂量与品质因数的计算

(1) 骨密度图像噪声：噪声是衡量图像质量的重要指标，在此只考虑由探测器记录的X射线强度统计特性引起的量子噪声，该噪声符合高斯分布，随着曝光量的增加而减小。对公式(1)进行误差分析^[17-19]，并根据MCNPX中相对误差R定义—计数结果平均值标准差与计数结果平均值之比，得到由I^L、I^H、I₀^L、I₀^H统计误差导致的骨密度图像噪声，用骨密度值标准差σ_mb表示：

为了方便比较分析，只需计算每幅DXA骨密度图像的噪声σ2mb平均值。获得Rs均值后，由模拟结果得到相对误差R2I0L、RIL2、R2I0H、RIH2平均值。因为能谱的有效能量相当于具有相同衰减效果的某一单能光子射束的辐射能量[20]，在计算噪声的平均值时，通过能谱的有效能量插值得到质量衰减系数等效值。

(2) 吸收剂量：用整个体模吸收剂量D表示患者所受的辐射剂量，因为MCNPX所得结果为相对剂量，为了得到总吸收剂量D(μGy)，计算如下：

式中，D_l、D_h分别为低能和高能照射时的吸收剂量，μGy/photon；N_l、N_h分别为低能和高能照射的入射粒子数。

(3) 品质因数FOM：最优化的DXA成像参数能够在保证目标噪声的前提下，使得患者所受的辐射剂量尽可能小，品质因数(FOM)是同时评价图像质量及辐射剂量的综合指标，但在不同文献中定义有所不同，本研究根据Bolin和Preuss提出的方法^[21-22]，将品质因数FOM表示为：

吸收剂量D与入射粒子数成正比例关系，当入射粒子数足够多时，图像噪声σ²_mb与入射粒子数成反比例关系，可知FOM与入射粒子数无关。

本研究针对常用的管电压取值区间40~200 kVp进行优化，并模拟大范围的入射粒子数比以及添加常见过滤铜片厚度观察其对品质因数FOM的影响规律。

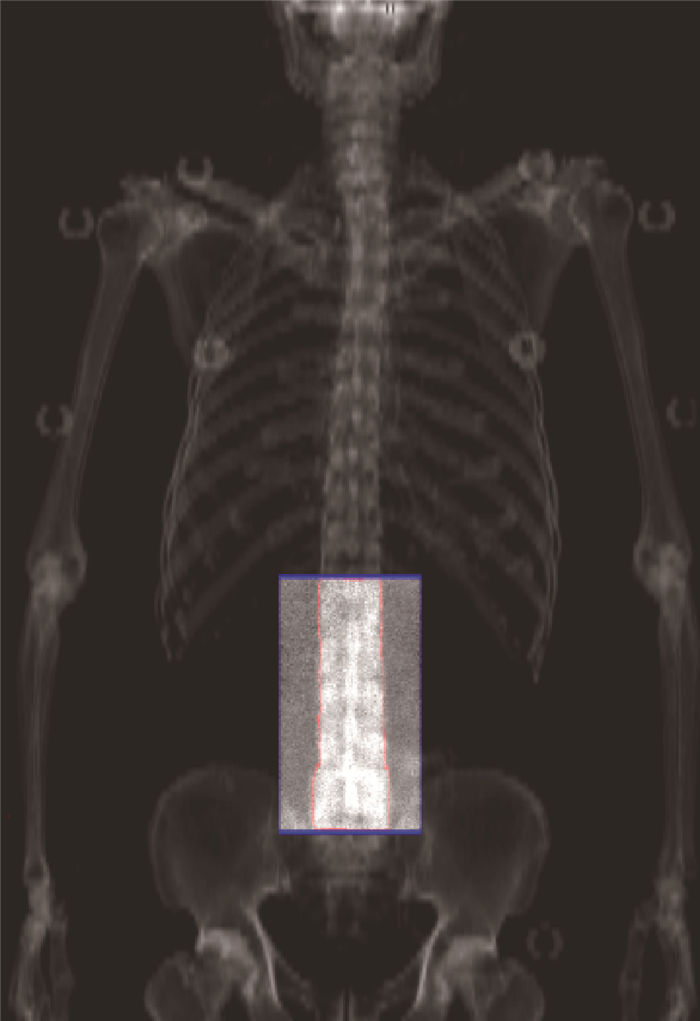
1.骨密度平均值计算：为了验证模拟是否正确，在获得骨密度图像后，计算了骨密度平均值，并与临床值比较。利用原始CT的HU值>300的像素投影，将其灰度叠加投影在一个平面上，划分骨骼和软组织区域，定位相关区域坐标，将骨密度的图像叠加在相应位置，如图 1所示。不同成像参数下骨密度计算平均值大约在0.6~1.5 g/cm²范围内，与临床值范围基本符合^[23]，并且由于图像噪声基于骨密度值标准差，表明图像噪声越低的同时骨密度值也越准确，管电压组合为80和200 kVp时，图像噪声较低，骨密度计算平均值为0.991 g/cm²，相比文献中70~79岁中国正常男性0.964 g/cm^2[23]，相对误差仅为0.028，验证了所建模型和模拟方法的正确性。

图 1 骨密度图像叠加在CT的灰度投影相应位置示意图 Figure 1 A bone density image superimposed on the corresponding position of the gray scale projection of CT

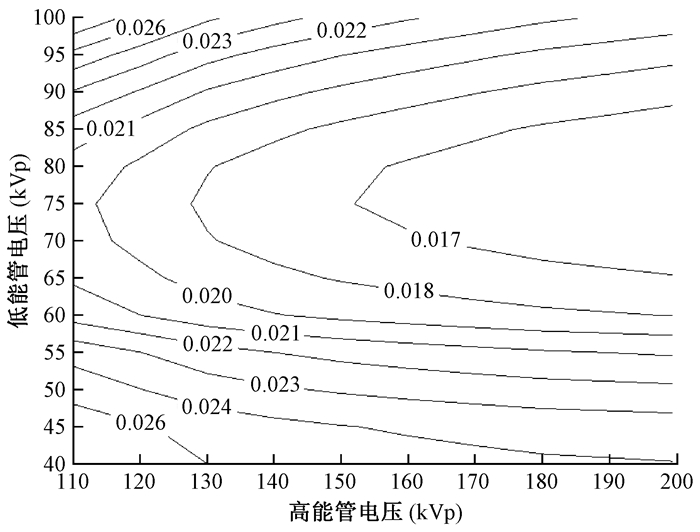
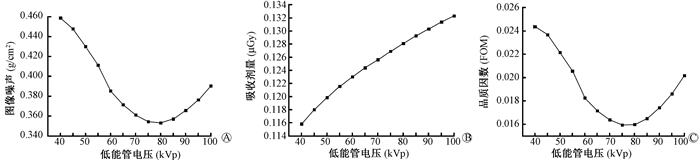
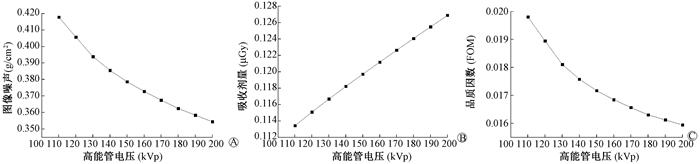
2.双能X射线管电压组合优化：低能管电压40~100 kVp，间隔5 kVp，共13组低能管电压数据，过滤片2.7 mm Al；高能管电压110~200 kVp，间隔10 kVp，共10组高能管电压数据，过滤片2.7 mm Al+ 0.3 mm Cu；入射粒子数比1 :1。不同高低能管电压组合得到130幅骨密度图像，计算每幅图的FOM。将FOM与不同管电压组合作等高线图，如图 2所示，低能取值在70~80 kVp，高能取值在160~200 kVp时，FOM值较小。由图 3和图 4可知，低能管电压为75 kVp，高能管电压为200 kVp时，FOM达到最低值1.59×10^-2。

图 2 管电压组合与品质因数关系图 Figure 2 Correlation of tube voltage combination with FOM

图 3 高能管电压固定为200 kVp与不同能量的低能管电压组合时，图像噪声、吸收剂量、品质因数变化规律图  A.图像噪声；B.吸收剂量；C.品质因数FOM Figure 3 Correlation of tube voltage combination with image noise, absorbed dose and FOM at combinations of 200 kVp high-energy tube voltage with different low-energy tube voltages  A. Image noise; B. Absorbed dose; C. FOM

图 4 低能管电压固定为75 kVp与不同能量的高能管电压组合时，图像噪声、吸收剂量、品质因数变化规律图   A.图像噪声；B.吸收剂量；C.品质因数FOM Figure 4 Correlation of tube voltage combination with image noise, absorbed dose and FOM at combinations of 75 kVp low-energy tube voltage with different high-energy tube voltages  A. Image noise; B. Absorbed dose; C. FOM

3.过滤铜片厚度优化：为了减少高低能谱之间的重叠，在产生高能能谱时额外添加一定厚度的过滤铜片，将高能能谱预硬化，过滤软X射线部分^[15]。产生高能能谱时，本研究在固定2.7 mm过滤铝片基础上添加的不同厚度的过滤铜片，管电压组合为55和120 kVp，入射粒子数比1 :1。由表 1可知，随着过滤铜片厚度增加，吸收剂量升高，图像噪声和FOM下降。

表 1(Table 1)

表 1 不同厚度的过滤铜片对应的吸收剂量、图像噪声和品质因数 Table 1 Absorbed dose, image noise, and FOM for different thicknesses of the Cu filter 铜片厚度 (mm) 吸收剂量 (μGy) 图像噪声 (g/cm2) 品质因数 (FOM) 0 0.102 0.788 6.30×10-2 0.1 0.106 0.554 3.25×10-2 0.3 0.110 0.448 2.20×10-2 3.0 0.124 0.389 1.87×10-2

表 1 不同厚度的过滤铜片对应的吸收剂量、图像噪声和品质因数 Table 1 Absorbed dose, image noise, and FOM for different thicknesses of the Cu filter

4.入射粒子数比优化：添加过滤铜片0.3 mm，管电压组合为70与200 kVp，保持总入射粒子数始终为1×10⁹，定义入射粒子数比r=N_l/N_h，r值分别为1 :3、1 :1、3 :2、3 :1、4 :1、9 :1、19 :1。如表 2所示，随着比值增加，吸收剂量降低，图像噪声和FOM先降低后升高，当r为3 :2时，图像噪声最小，当r为3 :1，FOM值最小。

表 2(Table 2)

表 2 不同入射粒子数比对应的吸收剂量、图像噪声和品质因数 Table 2 Absorbed dose, image noise, and FOM in relation to different incident photon number ratios 入射粒子数比Nl/Nh 吸收剂量(μGy) 图像噪声 (g/cm2) 品质因数 (FOM) 1:3 0.141 0.465 3.04×10-2 1:1 0.126 0.361 1.64×10-2 3:2 0.120 0.348 1.45×10-2 3:1 0.111 0.355 1.40×10-2 4:1 0.108 0.370 1.47×10-2 9:1 0.102 0.450 2.06×10-2 19:1 0.099 0.587 3.39×10-2

表 2 不同入射粒子数比对应的吸收剂量、图像噪声和品质因数 Table 2 Absorbed dose, image noise, and FOM in relation to different incident photon number ratios

当管电压取值在常用诊断能量区间40~200 kVp，正位腰椎成像情况下，模拟结果显示：低能管电压为70~85 kVp，高能管电压为160~200 kVp；产生高能能谱时额外添加0.3 mm过滤铜片；入射粒子数比r值为1~5，能在获得较好的DXA图像质量的同时使患者受到较小的辐射剂量。不同成像参数下图像质量差别较大，与模拟的最差参数相比，理想参数的选择使FOM值降低约14倍。

管电压组合优化结果显示，吸收剂量随着管电压取值增大而升高，当高能管电压固定时，低能管电压为80 kVp时图像噪声最小，75 kVp时FOM值最小；当低能管电压固定时，范围在200 kVp以下时，高能管电压取值越高，图像噪声和FOM值越低。双能X射线骨密度仪生成厂家美国Hologic公司，通过电压切换法产生70 kVp与140 kVp的能谱，美国Lunar公司、Norland公司以及Sopha公司通过K边缘过滤法产生的能谱为40 keV与70 keV^[13]，这说明目前大部分商用的骨密度仪能量选择不能达到最理想的成像效果。

为了分离双能X射线，在原有过滤铝片基础上添加过滤铜片，本研究结果显示，仅添加0.1 mm铜片，图像噪声和FOM明显下降；当过滤铜片选择0.3 mm时图像质量已明显提高，继续增加过滤铜片厚度，FOM值下降缓慢但是患者受到的辐射剂量却迅速增加。结果表明过滤铜片对图像质量有显著影响，但过度增加铜片厚度图像质量并不会有太大的提升反而会使患者受到更多不必要的辐射剂量。

相比高能X射线，低能X射线衰减更加严重，到达探测器的透射线更少，所以统计误差更大，入射粒子数比值r < 1，意味着更少的低能X射线，这种统计误差将大幅度增加，因此r值越小FOM值越大；r>1，意味着更多的低能X射线，这种统计误差将减小，但当r值过大时，高能的统计误差增大，FOM值升高。所以，r取值不应 < 1且不应过大，结果显示r值为1~5时FOM较小。本研究使用蒙特卡罗方法模拟骨密度成像，并计算骨密度值，将其与临床值相比较，验证了模拟的正确性。由模拟结果直接得到患者全身吸收剂量，根据MCNPX模拟结果误差定义计算得到图像噪声，从而获得FOM，优化了成像参数。相比以往研究中使用X射线平均能量来代替X射线能谱以及基于简单的几何模型，本文模拟了双能X射线能谱照射并基于真实人体CT数据构建的体素模型，所得结果更符合实际情况。

由于FOM还与组织的厚度和成分等因素有关^[23]，以上结果仅针对标准人体厚度的正位腰椎扫描，对于其他体型患者(肥胖患者、小孩等)以及其他人体部位(侧位腰椎、前臂骨等)在骨密度扫描时的参数选择会有所变化。另外本研究为理论模拟研究，只考虑了统计特性引起的噪声，未考虑实际噪声情况，但所得结果可为临床实际应用提供理论依据。