2. 421001 衡阳, 南华大学附属第一医院肿瘤放疗科
2. Department of Oncology, First Hospital Affiliated to University of South China, Hengyang 421001, China
蒙特卡罗方法[1]是一种模拟医用直线加速器粒子输运[2]及不均匀体模中剂量沉积的计算方法,其准确性已在许多研究中被证实[3-4]。使用蒙特卡罗方法模拟得到的剂量主要受加速器治疗头的几何尺寸以及射线参数的影响。治疗头的几何尺寸按照厂家提供的技术文档设置,因此正确的射线参数是确保剂量分布准确的关键。有关电子线平均能量、径向强度分布对不同射野下百分深度剂量影响的报道比较少,多数基于蒙特卡罗方法模拟加速器参数的研究,采用的是固定的电子线参数值或者只针对单一射野。通过将模拟与测量的剂量分布进行对比,本研究首次确定了不同大小射野下,模拟所需的最适电子线能量以及径向强度分布对百分深度剂量的影响。
材料与方法1.模拟程序及步骤:使用蒙特卡罗程序EGSnrc[5]模拟加速器中的粒子输运及水模体中的剂量沉积分为两步:首先,子程序BEAMnrc[6]产生包含粒子信息的相空间文件(粒子在治疗头输运过程中到达一个与靶特定距离且垂直于粒子入射方向的平面后,该粒子的能量、位置坐标、入射方向、权重等信息被储存在这个平面,得到的文件称为相空间文件);随后,该文件作为子程序DOSXYZnrc[7]的输入源,计算水模体中的剂量。
2. BEAMnrc中加速器治疗头建模:根据厂商提供的瓦里安IX加速器部件的几何尺寸和材料,使用SLABS、CONS3R、SLABS、FLATFILT、CHAMBER、MIRROR、JAWS模块分别模拟靶、初级准直器、真空窗、均整器、电离室、射野镜、次级准直器(上下铅门)。模拟的4个射野大小分别为4 cm×4 cm、10 cm×10 cm、20 cm×20 cm和30 cm×30 cm。相空间文件选择在垂直于粒子出射方向,源皮距(SSD)为100 cm处的平面上,方差减少技术选择直接韧致辐射分裂(directional bremsstrahlung splitting,DBS)[8]。入射电子束假设服从高斯径向强度分布(BEAMnrc中提供了多种类型的电子线源,使用不同的编号表示,本研究使用的是19号电子线源,其中包括电子线能量及径向强度分布等参数)。电子束设置为单能圆形平行束[6, 9]。在确定不同射野最适能量时,径向强度分布(由高斯分布的标准差给出,用符号σ表示)设置为0.1 cm[10],大小保持不变,得到所研究射野下不同能量值对应的百分深度剂量;在研究径向强度分布对不同射野下百分深度剂量的影响时,电子线能量设置为该射野下得到的最佳能量值,改变径向强度大小,研究其对百分深度剂量的影响。
3. DOSXYZnrc中水模剂量计算:将相空间文件作为输入源(DOSXYZnrc程序中同样需要设置输入源的类型,以相空间文件作为输入源的源号为2号),计算水模中的百分深度剂量。三维坐标方向互相垂直,其中Z轴为粒子入射方向,垂直向下,原点在水模上表面的中心点位置。水模大小为40 cm×40 cm×40 cm,划分成许多大小不同的体素,在x和y方向上,体素的长度均为1 cm,在z轴方向上体素的长度并不相同,水模表面1 cm深度内的长度为0.2 cm,超过1 cm深度后的长度为0.5 cm,采用这种设置可以减少模拟时间的同时,保证感兴趣区域的分辨率。电子步长算法和边界穿越算法分别使用PRESTA-Ⅱ和EXACT。
4.百分深度剂量的测量:百分深度剂量采用电离室(Semiflex 31010)进行测量。使用PTW公司三维水箱和电离室测量与模拟同等条件下水箱中心轴上的百分深度剂量。水模体的分辨率为0.1 mm,定位精度为±0.1 mm。扫描电离室的有效体积为0.125 cm3,腔体直径为5.5 mm。测量不同大小射野剂量分布,将电离室调节到水面的射野中心轴上,电离室有效测量点至放射源的距离为100 cm,测量射野中心轴上不同深度处的输出剂量率,归一到最大剂量深度处的输出剂量率,得到百分深度剂量。重复上述步骤,得到所研究的不同射野下的百分深度剂量。
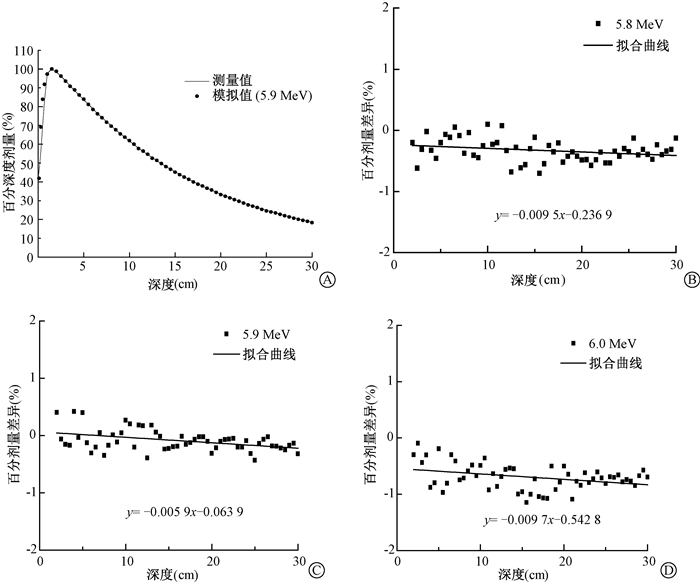
结果1.电子线能量:计算与测量的深度剂量均在水下1.5 cm处的最大剂量点进行归一化处理,得到各能量对应的百分深度剂量。对于4 cm×4 cm射野,电子线能量为5.9 MeV时模拟得到的百分深度剂量与测量的百分深度剂量如图 1所示。由于不同能量得到的百分深度剂量差异较小,为了分辨出最佳的能量值,计算出模拟与测量的百分剂量差,对该剂量差异进行最小二乘法拟合,得到了3个能量值对应的百分剂量差异曲线,如图 1所示。对于5.7~6.5 MeV区间内其他能量值对应的剂量差异也进行了拟合。拟合曲线中,斜率越接近于0、截距绝对值越小的曲线代表的电子线能量越理想。将该拟合方法应用于其他3个射野,得到适用于瓦里安Ⅸ加速器6 MV 4 cm×4 cm、10 cm×10 cm、20 cm×20 cm和30 cm×30 cm射野的蒙特卡罗电子线能量最佳值分别为5.9、6.0、6.3和6.4 MeV。4个不同射野下的模拟得到百分深度剂量在水模表面处均与测量值存在一定的差异。对于面积从小到大的4个射野,模拟与测量的深度剂量在最大剂量深度以下的剂量差异最大值分别为0.43%、1.04%、1.9%和2.21%。大射野下的百分深度剂量差异值略大于小射野下的值,但低于美国医学物理学家学会(AAPM)放射治疗委员会任务工作组50号报告中规定的剂量计算误差标准(5%)[11]。
|
图 1 5.9 MeV电子线能量得到的百分深度剂量及不同能量对应的百分剂量差 A.百分深度剂量;B~D.百分剂量差 Figure 1 Percentage depth dose curves calculated at 5.9 MeV electron energy and percentage dose differences at different energies A. Percentage depth dose curves; B-D. percentage dose differences |
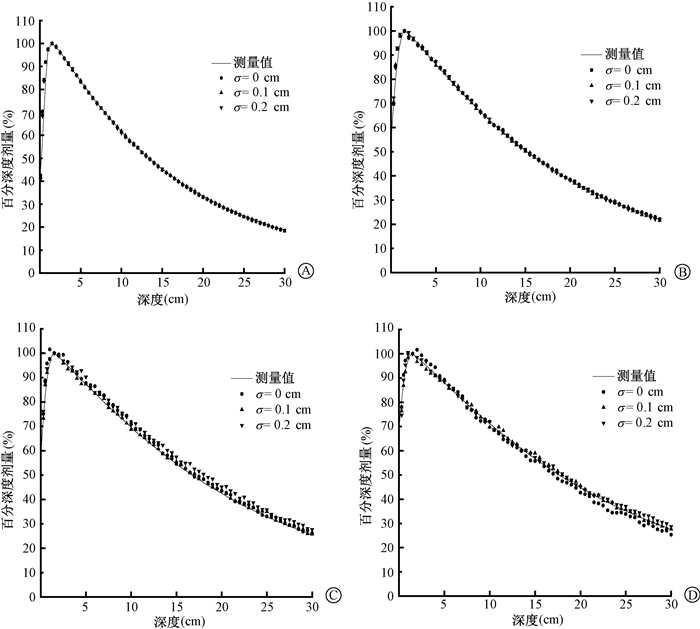
2.径向强度分布:每个射野下的电子线能量取最适能量值,改变径向强度分布,得到4组不同射野下的百分深度剂量曲线,如图 2所示。从图中可以看出,当σ变化时,4 cm×4 cm和10 cm×10 cm射野下模拟的百分深度剂量在剂量建成区内外均没有明显变化,与测量的深度剂量之间的差异也可忽略。但当射野尺寸为20 cm×20 cm和30 cm×30 cm,σ值取0及0.2 cm时,百分深度剂量与测量值之间的差异较明显,不能忽略。4组曲线中,水模表面的浅表剂量随着射野尺寸的增大而增加。
|
图 2 不同射野改变径向强度分布得到的百分深度剂量曲线 A. 4 cm×4 cm; B. 10 cm×10 cm; C. 20 cm×20 cm; D. 30 cm×30 cm Figure 2 Percentage depth dose curves calculated using three radial intensity distributions for different field sizes A. 4 cm×4 cm; B. 10 cm×10 cm; C. 20 cm×20 cm; D. 30 cm×30 cm |
讨论
使用蒙特卡罗方法模拟加速器产生的剂量分布关键是建立准确的模型,包括加速器几何模型以及电子束模型。在保证几何模型准确的前提下,确保模拟得到的剂量准确性主要是通过调整电子线参数来完成。本研究中采取一定的合理性近似,探究适用于各射野的最佳能量以及径向强度对深度剂量的影响:首先,在根据百分深度剂量确定电子线能量的同时,认为径向强度分布对深度剂量有较小的影响,或者其影响相对于能量对深度剂量的影响可以忽略[12],得到的能量值为最佳能量值;其次,在确定能量值后,改变径向强度大小,百分深度剂量的变化认为仅由径向强度引起。
有关电子线能量对百分深度剂量的影响,时颖华等[13]发现,对于10 cm×10 cm射野,不同电子线能量值对百分深度剂量没有明显影响,在确定适用于该射野的能量值时,将间隔为0.2 MeV的各能量得到的计算值与测量值进行比较,根据二者差异最大值,发现适用于该射野的能量值为5.8 MeV。本研究通过研究间隔为0.1 MeV各能量值,采用最小二乘拟合的方法,得到适用于该射野的能量值为6.0 MeV,两个能量值比较接近。此外,本研究扩展到多个射野,得到各射野的最佳能量值。倪昕晔等[14]对不同尺寸的射野下模拟与测量得到的百分深度剂量值进行比较,得到不同射野不同深度的剂量偏差,模拟时采用的是0号源,各个射野模拟时的电子线能量是固定值。Chibani等[15]基于厂商提供的电子线能量值,模拟了其对不同尺寸射野下剂量分布的影响。当能量改变0.2 MeV时,2 cm×2 cm、10 cm×10 cm、35 cm×35 cm射野下水模30 cm深度处的剂量与测量值有2%的误差。以上两个研究中电子线能量值的设置是根据经验值或者厂商提供的值,但在模拟过程中,有必要根据实际情况重新确定适用于加速器的电子线能量值。由于电子线能量的改变对百分深度剂量没有明显的影响,通过直接观察无法确定使误差最小的能量值,本研究通过对模拟与测量的剂量差值进行二次线性拟合[16],得到了在不同大小射野下的最适电子线能量。
关于径向强度分布对百分深度剂量影响的报道中,Tzedakis等[12]通过设置电子线能量为6 MeV,发现对于10 cm×10 cm射野,σ值取0~0.4 cm时,模拟与测量的百分深度剂量误差值低于1%。时颖华等[13]对10 cm×10 cm射野下径向强度分布对百分深度剂量的影响,得到了相似的结论。但对于大野及小野,国内外的相关的研究较少。在本研究中,首先确定最佳电子线能量后再改变径向强度,采用这种方法的优点是可以排除由能量引起的剂量不确定性,其次将研究的内容由单一射野扩展到小野以及大野。通过使用蒙特卡罗方法对瓦里安Ⅸ 6 MV加速器治疗头建模,改变射线参数,对模拟得到的百分深度剂量与测量的百分深度剂量进行对比,得到如下结论:
(1) 通过匹配由不同能量模拟得到的百分深度剂量与测量的百分深度剂量,发现适用于不同射野的最佳电子线能量略有不同。在电子线建模过程时,有必要找到准确的能量值,提高模拟精度。
(2) 对于4 cm×4 cm和10 cm×10 cm射野,改变径向强度分布,对百分深度剂量没有影响;对于20 cm×20 cm和30 cm×30 cm射野,径向强度分布对百分深度剂量的影响较明显。
(3) 适用于4 cm×4 cm、10 cm×10 cm、20 cm×20 cm、30 cm×30 cm射野的最佳电子线能量分别为5.9、6.0、6.3、6.4 MeV。对于20 cm×20 cm和30 cm×30 cm射野,当σ等于0.1 cm时,模拟与测量的百分深度剂量最为接近。
利益冲突 本研究还接受衡阳市科学技术发展计划项目(2016KJ36)资助,由署名作者按以下贡献说明独立开展,未接受有关公司的任何赞助,不涉及各相关方的利益冲突作者贡献声明 张帆负责模拟数据采集和论文撰写;伍海彪指导论文修改;肖爱农、艾小红、蔡曼波、李翩、成立祥协助实验;张振朝负责处理图像和数据;屈国普负责论文的选题
| [1] |
许淑艳. 蒙特卡罗方法在实验核物理中的应用[M]. 北京: 原子能出版社, 2006, 73-121. Xu SY. Application of Monte Carlo method in experimental nuclear physics[M]. Beijing: Atomic Energy Press, 2006, 73-121. |
| [2] |
Verhaegen F, Seuntjens J. Monte Carlo modeling of external radiotherapy photon beams[J]. Phys Med Biol, 2003, 48(21): R107-R164. DOI:10.1088/0031-9155/48/21/R01 |
| [3] |
Andreo P. Monte Carlo techniques in medical radiation physics[J]. Phys Med Biol, 1991, 36(7): 861-920. DOI:10.1088/0031-9155/36/7/001 |
| [4] |
Rogers DWO, Bielajew AF. Monte Carlo techniques of electron and photon transport for radiation dosimetry[J]. Dosim Ion Radiat, 1990, 3: 427-539. |
| [5] |
Kawrakow I, Mainegra-Hing E, Rogers DWO, et al. The EGSnrc code system:Monte Carlo simulation of electron and photon transport[M]. Ottawa: National Research Council Canada, 2009, 27-104.
|
| [6] |
Rogers DWO, Walters BRB, Kawrakow I. Beamnrc users manual[M]. Ottawa: National Research Council Canada, 2009, 18-114.
|
| [7] |
Walters BRB, Kawrakow I, Rogers DWO. Dosxyznrc users manual[M]. Ottawa: National Research Council Canada, 2009, 10-70.
|
| [8] |
Kawrakow I, Rogers DWO, Walters BRB. Large efficiency improvements in BEAMnrc using directional bremsstrahlung splitting[J]. Med Phys, 2004, 31(10): 2883-2898. DOI:10.1118/1.1788912 |
| [9] |
Sheikh-Bagheri D, Rogers DWO. Sensitivity of megavoltage photon beam Monte Carlo simulations to electron beam and other parameters[J]. Med Phys, 2002, 29(3): 379-390. DOI:10.1118/1.1446109 |
| [10] |
Keall PJ, Siebers JV, Libby B, et al. Determining the incident electron fluence for Monte Carlo-based photon treatment planning using a standard measured data set[J]. Med Phys, 2003, 30(4): 574-582. DOI:10.1118/1.1561623 |
| [11] |
International Commission on Radiation Units and Measurements. ICRU 50. Prescribing, recording and reporting photon beam therapy[R]. Bethesda: ICRU, 1993.
|
| [12] |
Tzedakis A, Damilakis JE, Mazonakis M, et al. Influence of initial electron beam parameters on Monte Carlo calculated absorbed dose distributions for radiotherapy photon beams[J]. Med Phys, 2004, 31(4): 907-913. DOI:10.1118/1.1668551 |
| [13] |
时颖华, 周凌宏, 刘迎军, 等. 6 MV医用电子直线加速器的蒙特卡罗模拟[J]. 中华放射医学与防护杂志, 2011, 31(2): 220-224. Shi YH, Zhou LH, Liu YJ, et al. Monte Carlo simulation of 6 MV medical electron linear accelerator[J]. Chin J Radiol Med Prot, 2011, 31(2): 220-224. DOI:10.3760/cma.j.issn.0254-5098.2011.02.028 |
| [14] |
倪昕晔, 汤晓斌, 耿长冉, 等. 加速器百分深度剂量蒙特卡罗模拟计算准确性研究[J]. 中华放射肿瘤学杂志, 2013, 22(1): 64-67. Ni XY, Tang XB, Geng CR, et al. Study on accurateness of percentage depth dose with Monte Carlo simulation algorithm[J]. Chin J Radiat Oncol, 2013, 22(1): 64-67. DOI:10.3760/cma.j.issn.1004-4221.2013.01.020 |
| [15] |
Chibani O, Moftah B, Ma CM. On Monte Carlo modeling of megavoltage photon beams:a revisited study on the sensitivity of beam parameters[J]. Med Phys, 2011, 38(1): 188-201. DOI:10.1118/1.3523625 |
| [16] |
Almberg SS, Frengen J, Kylling A, et al. Monte Carlo linear accelerator simulation of megavoltage photon beams:independent determination of initial beam parameters[J]. Med Phys, 2012, 39(1): 40-47. DOI:10.1118/1.3668315 |
 2018, Vol. 38
2018, Vol. 38


