肿瘤乏氧与放射治疗失败有密切关系，乏氧会降低放射敏感性和局部控制率。在常规放射治疗过程中，肿瘤乏氧导致的放射抗拒因分次间的再氧合过程而减小，而在大分割治疗中，由于疗程短次数少，肿瘤乏氧问题更应该得到重视。对肿瘤内部乏氧区域给予一定比例的高剂量，可以有效提高肿瘤控制率^[1-3]。

目前在立体定向体部放射治疗(SBRT)的计划设计中，靶区内部的剂量没有一个明确的规定。本研究的目的在于通过两种不同的肿瘤控制率(TCP)模型研究乏氧区的同步推量(SIB)对肿瘤控制率的影响，分析TCP与靶区不同预测因子(最大剂量D_max、平均剂量D_mean和最小剂量D_min)之间的关系，给出不同乏氧状态下靶区内部剂量的预测值，给SBRT计划的剂量设计提供一种有效的方式。同时，由于SBRT单次剂量大且剂量分布不均匀，而胰腺癌紧靠胃、小肠、十二指肠、结肠等危及器官，摆位误差引起的偏差对靶区和正常组织的影响需要特别关注。

1.临床资料：采集浙江大学医学院附属第二医院放疗科2015年7月至2017年4月接受SBRT治疗的局部进展期胰腺癌(LAPC)患者10例，平均年龄62岁，计划靶区(PTV)平均体积63.2 cm³，内靶区(ITV)平均体积21.4 cm³。靶区最高剂量范围为123%~126%，平均值为125%。所有患者均已签署知情同意书。

2.靶区勾画与计划设计：CT扫描过程中所有患者仰卧于SBRT专用真空垫，置于一体板中，并用压腹杆进行压腹固定。在美国GE LightSpeed放疗定位机上行4D-CT扫描，层厚为2.5 mm。参考4D-CT 10个时相勾画出ITV，再将ITV左右、头脚、前后分别外放5 mm得到PTV。

处方剂量参考国际上LAPC的SBRT治疗临床经验，采用30 Gy/5次进行照射^[4-5]。通过调强适形(IMRT)技术实现对靶区内部的同步推量，要求100%的参考剂量线包络90%的PTV，110%的参考剂量线包络95%的ITV。

3.数据获取：在美国瓦里安公司Trilogy医用加速器进行kV-CBCT摆位校正，治疗前行第1次锥形束CT(CBCT)，治疗后行第2次CBCT，治疗前后共获取100组摆位校正数据。在美国瓦里安公司Eclipse 10.0计划系统中按照治疗前后获取的配准数据分别对原始计划P的射野中心进行偏移，形成计划P1和P2，记录单次治疗中PTV和ITV分别接受100%剂量和110%的剂量的体积以及各危及器官(胃D_{5 cc}、小肠D_{5 cc}、十二指肠D_{5 cc}、结肠D_{5 cc}、脊髓D_max、肾脏D_33%)的点剂量。分别计算3组治疗计划(P、P1、P2)中每个计划的靶区覆盖率(TC)：

式中，V_TV为目标靶区的体积; V_ref为100%或110%的剂量线包络的体积。

4.TCP模型：单次剂量不超过8 Gy时，研究表明线性二次(L-Q)模型能够很好地预测细胞存活曲线^[6-7]。将ITV定义为乏氧区，RTV(PTV减去ITV的环状部分)定义为富氧区。为使整个PTV达到相同的肿瘤控制率，富氧区和乏氧区应该具有相同的细胞存活数。由L-Q模型^[8]及Carlson等^[9]提出的模型得出：

式中，氧增强比(OER)为产生相同生物效应时，乏氧细胞与富氧细胞的剂量之比; α和β分别表示不可修复损伤和可修复损伤，(α/β)_o和(α/β)_h分别代表富氧区和乏氧区的α/β值。在已知(α/β)_o的情况下可以得出(α/β)_h的值，带入模型即可计算出乏氧区的TCP值。采用两种不同的TCP模型进行计算，分别是Niemierko模型^[10]和Poisson模型^[11]。模型的具体参数参考相关文献^[11-13]。

通过编写的MATLAB程序调用积分量体积直方图(DVH)中的剂量体积向量，将其转化为微分剂量体积向量，再将剂量等效为单次2 Gy下的剂量(EQD₂)，通过公式即可求出各计划TCP的值。分别计算出乏氧区和富氧区的TCP以后，两者相乘即为PTV的TCP。

5.统计学处理：采用SPSS 19.0对数据进行分析。数据均符合正态分布。对两种模型的TCP与靶区剂量相关因子(D_max、D_mean和D_min)做Pearson相关性分析。对预测剂量D_mean与乏氧区肿瘤控制率TCP_ITV做一元线性回归。P<0.05为差异具有统计学意义。

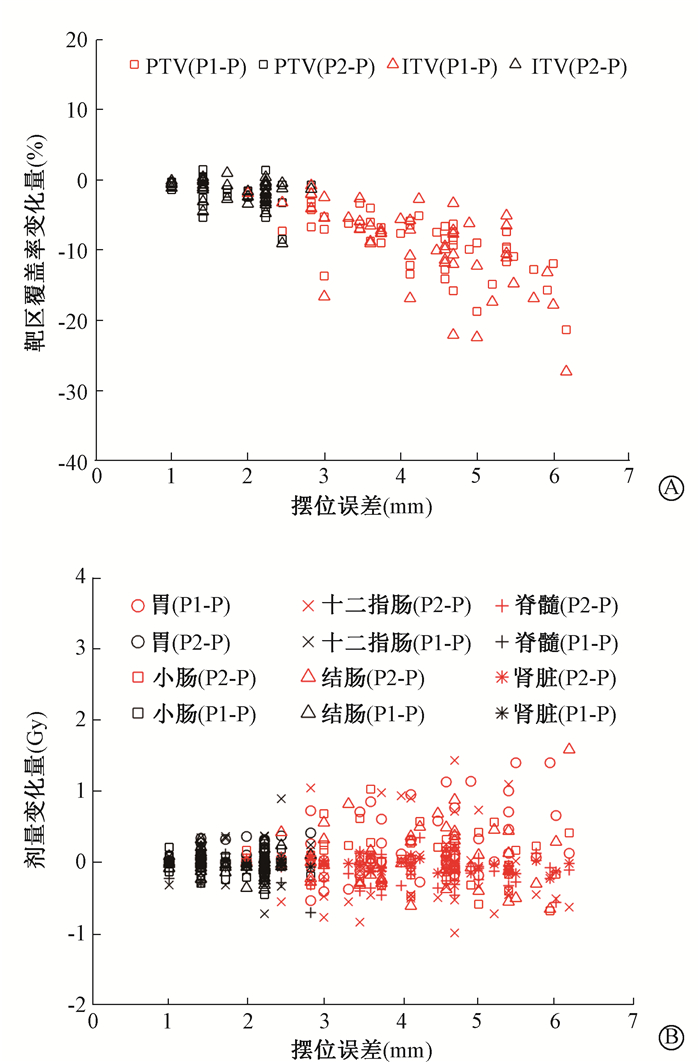
1.剂量非均匀性对靶区和危及器官的影响：图 1显示了单次治疗计划中PTV和ITV的靶区覆盖率变化量与摆位误差三维方向偏移的关系。原始计划P中PTV的TC平均值为95.7%，ITV的TC平均值为98.0%。当摆位误差三维方向偏移在<2 mm时，TC的变化较小；当偏移>2 mm时，TC的变化开始快速增大。在计划P2中，PTV的TC平均值下降至94.1%，ITV的TC平均值下降至96.7%。在计划P1中，PTV的TC平均值下降至86.8%，ITV的TC平均值下降至88.8%。

图 1 靶区覆盖率和危及器官剂量变化量随摆位误差的变化A.靶区覆盖率变化量；B.危及器官剂量变化量 注：PTV.计划靶区；ITV.内靶区；P1-P.计划P1与原始计划P的计算量之差；P2-P.计划P2与原始计划P的计算量之差 Figure 1 Changes of TC and OAR doses over setup errors A. Difference of target coverage; B. Difference of OAR doses

分别统计单次治疗计划中危及器官剂量，为了便于比较，将危及器官剂量统一转化为EQD₂表示。图 1显示了危及器官的剂量变化量与摆位误差三维方向偏移的关系。各危及器官剂量的最大增加值出现的位置范围为3.6~6.2 mm。计划P1和计划P2中的危及器官偏差的平均值范围分别为-0.11~0.26 Gy和-0.05~0.08 Gy。危及器官的剂量变化总体随摆位误差的增大而增大，但不同器官变化的趋势并不一致，相较于计划P2，计划P1中对应的危及器官剂量的波动范围更大，增加的幅度也更大。

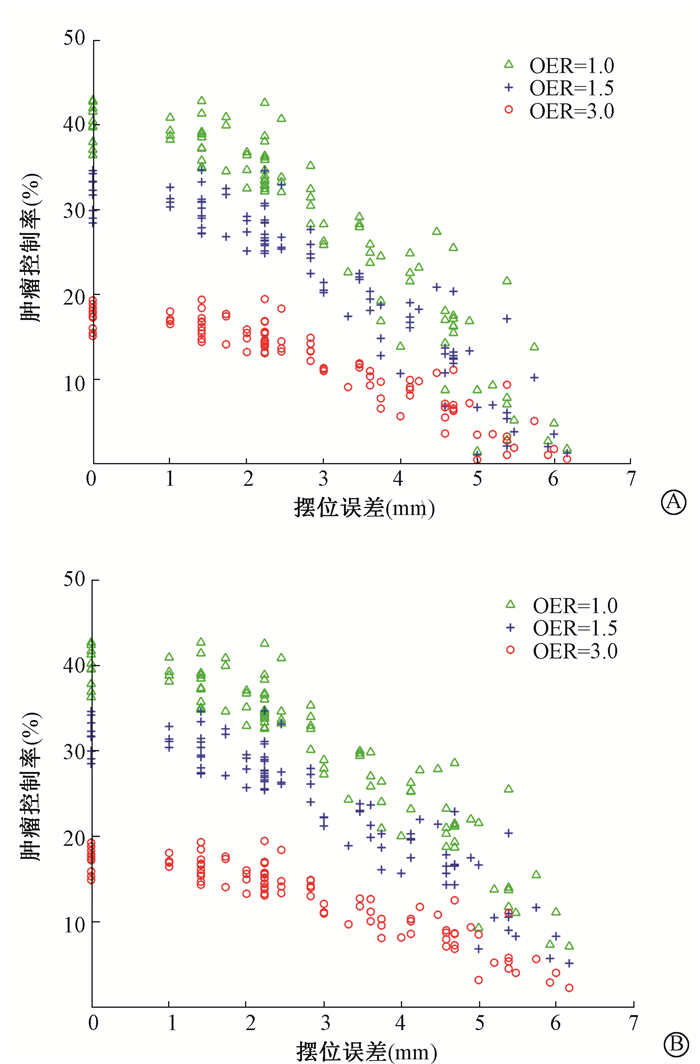
2.乏氧区同步推量的分析：图 2所示为Niemierko模型和Poisson模型中OER为1.0、1.5和3.0时PTV的肿瘤控制率随摆位误差的变化值。本研究中参考腺癌取值，选取胰腺癌富氧区RTV的(α/β)_o为6 Gy^[14]，对应的乏氧区ITV的(α/β)_h为6、9和18 Gy。两种模型的计算结果在2 mm摆位误差内基本无差别，当误差继续增大时，Niemierko模型相对Poisson模型下降更快一点，在三维方向的偏移达到6 mm时TCP接近于0。

图 2 两种模型不同氧增强比时的PTV肿瘤控制率随摆位误差的变化  A. Niemierko模型；B. Poisson模型 Figure 2 Changes of TCP with different OER over setup corrections  A. Niemierko model; B. Poisson model

统计治疗前后因摆位误差形成的共100个P1和P2计划中两种模型的TCP与靶区剂量相关因子之间的关系。TCP与靶区D_max、D_mean和D_min的关系在不同剂量分布时会有所变化，但D_mean始终是一个比较稳定的预测因子。不论是RTV还是不同OER时的ITV，TCP与D_mean关系密切，Pearson相关性系数均超过0.9，如表 1所示。

表 1(Table 1)

表 1 两种模型不同靶区剂量的相关性分析 Table 1 Pearson correlation between target volume and doses for two models 模型 因子 TCPRTV TCPITV (OER=1.0) TCPITV (OER=1.5) TCPITV (OER=3.0) r值 P值 r值 P值 r值 P值 r值 P值 Niemierko Dmax -0.365 0.000 0.052 0.609 0.043 0.673 0.029 0.777 Dmean 0.901 0.000 0.976 0.000 0.983 0.000 0.984 0.000 Dmin 0.942 0.000 0.743 0.000 0.740 0.000 0.736 0.000 Poisson Dmax -0.360 0.000 0.041 0.685 0.041 0.687 0.038 0.711 Dmean 0.930 0.000 0.979 0.000 0.987 0.000 0.992 0.000 Dmin 0.915 0.000 0.741 0.000 0.728c 0.000 0.714 0.000 注：TCPRTV.富氧区RTV的肿瘤控制率；TCPITV.乏氧区ITV的肿瘤控制率；OER.氧增强比

表 1 两种模型不同靶区剂量的相关性分析 Table 1 Pearson correlation between target volume and doses for two models

在TCP_RTV已知的情况下，为使ITV和RTV达到相同的肿瘤控制率，分别预测出OER为不同值时两种模型中ITV的D_mean需要达到的剂量。如表 2所示，通过对D_mean与TCP_ITV做一元线性回归，可以找出D_mean与TCP_ITV的对应关系。当氧增强比不同时，D_mean需要达到的剂量差别很大，范围从31.4 Gy到37.2 Gy。胰腺癌的OER接近于3.0，此时ITV的D_mean预测值为37.2 Gy，相当于处方剂量的1.24倍。原始计划P中ITV的D_mean为35.6 Gy，预示着还有提升空间。

表 2(Table 2)

表 2 两种模型乏氧区平均剂量的预测值 Table 2 Predictive values of ITV Dmean for two models 模型 OER 预测值(Gy) 调整R2 F值 P值 Niemierko 1.0 31.4 0.952 1 979.1 0.000 1.5 34.0 0.966 2 777.5 0.000 3.0 37.2 0.969 3 069.5 0.000 Poisson 1.0 31.6 0.957 2 210.1 0.000 1.5 33.9 0.973 3 574.5 0.000 3.0 37.2 0.984 6 241.0 0.000 注：OER.氧增强比

表 2 两种模型乏氧区平均剂量的预测值 Table 2 Predictive values of ITV Dmean for two models

从统计结果来看，靶区覆盖率随摆位误差的增大波动很大。摆位误差的增加会明显影响靶区覆盖率和危及器官的剂量，治疗前摆位误差会对靶区和危及器官产生较大的影响，而治疗过程中的摆位误差对靶区和危及器官的影响极大地减小。对靶区覆盖率而言，摆位误差的大小是主要因素，当摆位误差较小时，靶区的影响也很小。对危及器官而言，其不仅与摆位误差相关，本身的解剖结构以及与靶区的相邻关系等因素也可能对剂量评估产生影响。本研究表明，治疗过程中患者的呼吸运动以及位置移动等引起的摆位误差可忽略，原因与SBRT一体定位板以及压腹杆的固定效果较好有关。Case等^[15]和Shimohigashi等^[16]分别在肝癌SBRT的研究中通过CBCT摆位误差验证发现，治疗过程中的位置变化很小。Heinzerling等^[17]研究发现，压腹措施和良好的固定装置能够极大地缩小治疗过程中的器官运动。

本研究采用了两种不同的肿瘤控制率模型来计算肿瘤在不同乏氧状态下的TCP。结果表明，不考虑肿瘤的乏氧问题将会对肿瘤控制率的计算产生很大的影响。在常规放射治疗过程中，由于治疗疗程的周期较长，肿瘤和危及器官存在变化，对靶区剂量的最高量以及均匀性要求较高。但在SBRT治疗过程中，由于图像引导技术和4DCT的广泛使用，以及治疗次数的极大缩短和摆位误差的减小，给乏氧区推量以提高肿瘤控制率是一个较好的选择。Popple等^[18]的研究认为，乏氧区的同步推量应该达到处方剂量的1.2~1.3倍；Tomé等^[3]的研究认为，乏氧区剂量应达到处方剂量的120%~150%，结论均与本研究结果保持一致。剂量提升可能会导致危及器官的风险变大，只要能够在ITV的D_mean提升的同时，较好地控制RTV的剂量的上升，危及器官剂量变化较小。

由于机器条件所限，文中没有计算旋转误差对剂量带来的影响。本研究中旋转误差均<1°，其对靶区和周围器官剂量的影响可以忽略^[19]。另外，TCP计算模型中将乏氧细胞视为静止且位于中心的理想状态，而实际的肿瘤乏氧细胞状态可能会不断变化，其对肿瘤控制率可能造成影响^[18]，需要做进一步深入探讨。

综上所述，治疗过程中的位置偏差对靶区覆盖率和危及器官的影响较小。肿瘤乏氧问题对肿瘤控制率影响很大。为消除乏氧对肿瘤控制的影响，应该将胰腺癌乏氧区的D_mean提高到处方剂量的1.24倍以上。