中华放射医学与防护杂志  2018, Vol. 38 Issue (11): 859-864   PDF    
引用本文
吴爱林, 吴爱东, 朱磊, 刘云琴, 钱立庭. 瓦里安高剂量率铱源剂量学参数的蒙特卡罗模拟研究[J]. 中华放射医学与防护杂志, 2018, 38(11): 859-864, DOI: 10.3760/cma.j.issn.0254-5098.2018.11.012.
瓦里安高剂量率铱源剂量学参数的蒙特卡罗模拟研究
吴爱林1 , 吴爱东1 , 朱磊2 , 刘云琴1 , 钱立庭1     
1. 230031 合肥, 中国科学技术大学附属第一医院 安徽省肿瘤医院肿瘤放射治疗室;
2. 230026 合肥, 中国科学技术大学物理学院
收稿日期: 2018-02-06
通信作者: 吴爱东, Email:aidongwu@21cn.com
[摘要] 目的 采用美国医学物理师学会（AAPM）和欧洲放射治疗和肿瘤学会（ESTRO）推荐的蒙特卡罗方法对瓦里安GammaMed Plus HDR 192Ir源的剂量学参数进行模拟研究。方法 基于EGSnrc蒙特卡罗软件，建立该型号192Ir源精确的计算模型。采用公式推导、双线性插值及单位转换等方法，分别得到了单位活度空气比释动能强度、剂量率常数、径向剂量函数以及各向异性函数，并将结果与文献报道数据进行分析比较。结果 研究得到的单位活度空气比释动能强度为9.781×10-8 U/Bq，剂量率参数为1.113 cGy·h-1·U-1，与文献报道的相差在0.4%以内。本研究的径向剂量函数、各向异性函数与文献数据能较好吻合。结论 基于EGSnrc蒙特卡罗软件能对192Ir源剂量学特性进行定量研究，这将为进一步研究后装剂量分布，精确评价临床放疗剂量提供理论依据。
[关键词] 近距离后装治疗     192Ir源     蒙特卡罗模拟     剂量学参数    
Monte Carlo simulation study of dosimetric parameters of Varian HDR 192Ir source
Wu Ailin1, Wu Aidong1, Zhu Lei2, Liu Yunqin1, Qian Liting1     
1. Tumor Radiotherapy Room, The First Affiliated Hospital of University of Science and Technology of China, Anhui Provincial Cancer Hospital, Hefei 230031, China;
2. School of Physical Sciences, University of Science and Technology of China, Hefei 230026, China
Corresponding author: Wu Aidong, Email:aidongwu@21cn.com
[Abstract] Objective To study the dosimetric parameters of Varian GammaMed Plus HDR 192Ir source via Monte Carlo (MC) method based on the recommendation of the American Association of Physicist in Medicine (AAPM) and European Society for Radiotherapy and Oncology (ESTRO). Methods Using the Monte Carlo program EGSnrc, an accurate model of 192Ir source for MC calculations was establish firstly. Through formula derivation, bilinear interpolation and unit conversion, the air kerma strength per unit source activity, the dose rate constant, radial dose function and anisotropy function was obtained then, and compare the result with those in other published studies. Results The air kerma strength per unit source activity was 9.781×10-8 U/Bq. The dose rate constant was 1.113 cGy·h-1·U-1, with a discrepancy of less than 0.4% compared with result published in other works. Furthermore, the curves of radial dose function and anisotropy function overall agree with the data shown in the literature. Conclusions The feasibility of performing dosimetric studies of 192Ir source using the MC software EGSnrc was demonstrated. This work provides a theoretical guidance on analysis of the dose distribution of brachytherapy and on evaluation of the dose accuracy of clinical radiotherapy.
[Key words] Brachytherapy     192Ir source     Monte Carlo simulation     Dosimetric parameters    

近年来，基于多种放射源的近距离后装治疗在国内的临床应用及研究日益广泛[1-2]。在近距离后装治疗中，高剂量率(HDR)192Ir放射源在组织中的剂量分布将直接决定患者的治疗效果，因此有必要采用不同理论及研究方法对192Ir源的剂量学特性进行系统定量的评估。由于实验方法很难准确测量距源很近位置处的剂量率，欧洲放射治疗和肿瘤学会(ESTRO)[3]、美国医学物理师学会(AAPM)的TG-43号[4]以及TG-43U1号[5]报告推荐在临床使用前采用蒙特卡罗程序对放射源剂量学参数进行模拟研究。目前，国内还少见关于瓦里安GammaMed Plus HDR 192Ir源的剂量学参数研究报道，本研究拟采用EGSnrc蒙特卡罗程序对该机型的192Ir源剂量学特性做系统定量的分析，并将结果与其他文献报道数据进行比较，检验本研究模拟计算的准确性。

材料与方法

1.剂量学参数计算公式：在AAPM的TG-43U1号[5]报告中，推荐近距离治疗水模体中吸收剂量率极坐标下的计算公式如式(1)所示：

$ \dot D\left( {r,\theta } \right) = {S_k} \cdot \Lambda \cdot \frac{{{G_L}\left( {r,\theta } \right)}}{{{G_L}({r_0},{\theta _0})}} \cdot {g_L}\left( r \right) \cdot F\left( {r,\theta } \right) $ (1)

式中，r为空间任一点到放射源中心点的距离，cm；θ为空间中任一点与放射源中心轴(即放射源长轴方向)的夹角；Sk为空气比释动能强度，${S_{\rm{k}}} = {{\dot K}_\delta }\left(d \right) \cdot {d^2}$，U或cGy·cm2·h-1；${{\dot K}_\delta }$为自由空间的空气比释动能率，cGy/h；d取100 cm。Λ为剂量率常数，其定义为放射源在水中参考位置(1 cm，$\frac{\pi }{2}$)处的吸收剂量率与Sk的比值，即$\mathit{\Lambda } = \frac{{\dot D\left({{r_0}, {\theta _0}} \right)}}{{{S_k}}}$，cGy·h-1 · U-1。GL(r, θ)为线源几何因子，代表源本身因几何形状和内部活性分布对射源周围剂量率的影响。其定义如(2)式所示。径向剂量函数gL(r)和各向异性函数F(r, θ)的计算公式分别为(3)和(4)。这些剂量函数可以通过实验测量和蒙特卡罗模拟两种方法得到，但由于实验测量精度受测量手段和设备影响较大，实现难度较大且花费较高，因此，本研究拟采用蒙特卡罗程序对铱源的剂量学特性做系统研究。

式(2)中，L为源有效活性长度，cm；β为任意点对射源前后端的夹角。

$ {G_L}\left( {r,\theta } \right) = \left\{ {\begin{array}{*{20}{c}} {\frac{\beta }{{L \cdot r \cdot {\rm{sin}}\theta }}}&{\theta \ne 0}\\ {\frac{1}{{{r^2} - \frac{{{L^2}}}{4}}}}&{\theta = 0} \end{array}} \right. $ (2)
$ {g_L}\left( r \right) = \frac{{\dot D(r,{\theta _0})}}{{\dot D({r_0},{\theta _0})}} \cdot \frac{{{{\dot G}_L}({r_0},{\theta _0})}}{{{{\dot G}_L}(r,{\theta _0})}} $ (3)
$ F\left( {r,\theta } \right) = \frac{{\dot D\left( {r,\theta } \right)}}{{\dot D(r,{\theta _0})}} \cdot \frac{{{{\dot G}_L}(r,{\theta _0})}}{{{{\dot G}_L}\left( {r,\theta } \right)}} $ (4)

经公式推导及单位转换，本研究中将计算单位活度空气比释动能强度，如(5)式所示：

$ \begin{array}{l} \frac{{{S_{\rm{k}}}}}{A} = 1.602 \times {10^{ - 10}} \times 2.363 \times 3.6 \times {10^9} \times \\ \quad \quad \sum\limits_{{E_{{\rm{min}}}}}^{{E_{{\rm{max}}}}} {\phi {{\left( E \right)}_i}} \cdot \left( {\frac{{{\mu _{{\rm{en}}}}\left( {{E_{\rm{i}}}} \right)}}{\rho }} \right) \cdot \Delta E \end{array} $ (5)

式中，A为放射源活度, Bq；ϕ(Ei)为处于能量Ei[MeV]处的能量通量；$\frac{{{\mu _{{\rm{en}}}}\left({{E_i}} \right)}}{\rho }$是能量为Ei(MeV)时，干燥空气的质能吸收系数；ΔE是指模拟计算中设置的最小能量步长而Ei是每个能量步长中心点对应的能量值。

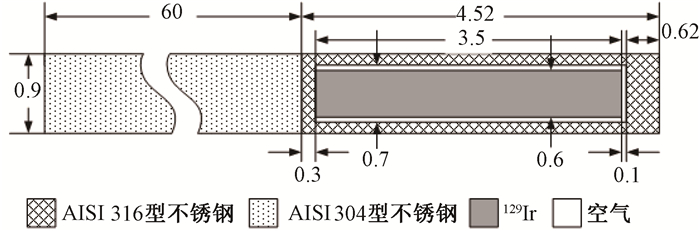
2.GammaMed Plus HDR 192Ir源模型：192Ir的半衰期约为73.825 d，其平均每次衰变发出1个电子和2.363个光子。辐射γ光子的能量为50~800 keV，平均能量约为370 keV。美国瓦里安GammaMed Plus HDR 192Ir源的几何结构和组成材料见图 1[6-7]。有效铱源呈圆柱状，其有效活性长度为3.5 mm，直径为0.6 mm，被直径为0.9 mm的AISI 316 L型不锈钢包裹，不锈钢包壳与裸源间存在小范围的空气间隔。此外，计算模型还加入了长60 mm，直径0.9 mm的AISI 304型不锈钢传输缆线的影响。计算模型中使用的各材料组成及密度如表 1所示。

图 1 GammaMed Plus HDR 192Ir源材料及结构尺寸(mm) Figure 1 Materials and dimensions of GammaMed Plus HDR 192Ir source(mm)

表 1 本研究模拟计算使用的材料组成和密度 Table 1 Materials, composition and density used in this simulation study

3.蒙特卡罗程序及其模拟参数：本研究模拟电子-光子传输过程的EGSnrc蒙特卡罗软件系统受到了目前医学物理领域的广泛认可，适用于模拟1 keV~10 GeV的粒子能量范围。在本研究中，采用了最新版的EGSnrc版本[8]来计算光子通量和水中吸收剂量。

模拟中使用XCOM光子截面库和“Ir192_bare_1993” 192Ir源能谱，每次模拟统计的粒子数为109。在利用FLURZnrc子程序计算源附近的能谱分布时，将放射源置于长100 cm，半径50 cm的圆柱体中心。根据文献建议，将能量步长选择为5 keV，电子和光子的截止能量设置为2 MeV和10 keV[6-7, 9]。采用DOSRZnrc模块计算水模体中的吸收剂量率，考虑背散射等因素影响，放射源置于长50 cm，半径为25 cm的圆柱体水模体中心。为保证计算效率和记录精度，在距源不同远近位置划分不同大小的体元，如在距源中心距离r≤1 cm，采用0.1 mm3体元；在1 cm＜r≤5 cm范围，采用0.5 mm3体元；在5 cm＜r≤10 cm范围，采用1 mm3体元；在10 cm＜r≤20 cm范围，使用2 mm3体元。为去除放射源包壳产生低能光子影响，将电子和光子的截止能量设置为0.521 MeV和10 keV。

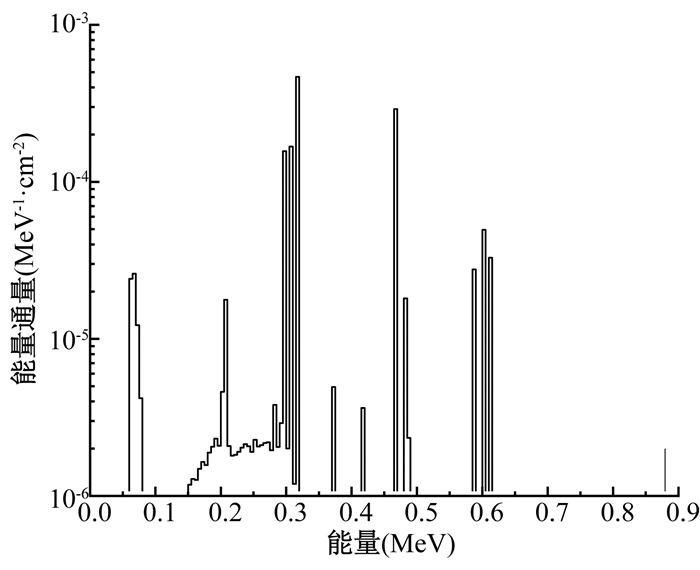
结果

1.单位活度空气比释动能强度和剂量率常数：利用FLURZnrc程序计算得出了距源中垂线1 m处的光子能谱分布(图 2)。利用DOSRZnrc程序计算出水模体中各位置处的吸收剂量，再经公式推导及单位转换[9]，进而得出单位活度空气比释动能强度和剂量率常数，模拟中统计误差均 < 1%。本研究得出的单位活度空气比释动能强度Sk/A为9.781×10-8 U/Bq，与文献[7]给出的9.790×10-8 U/Bq，仅相差0.092%；本研究得出的剂量率常数Λ为1.113 cGy·h-1·U-1，与文献[6-7]的研究结果(1.115 cGy·h-1·U-1和1.117 cGy·h-1·U-1)吻合较好，分别相差0.180%和0.359%。

图 2 距源中心1 m处的能谱分布图 Figure 2 Fluence spectra at 1 m from the center of source

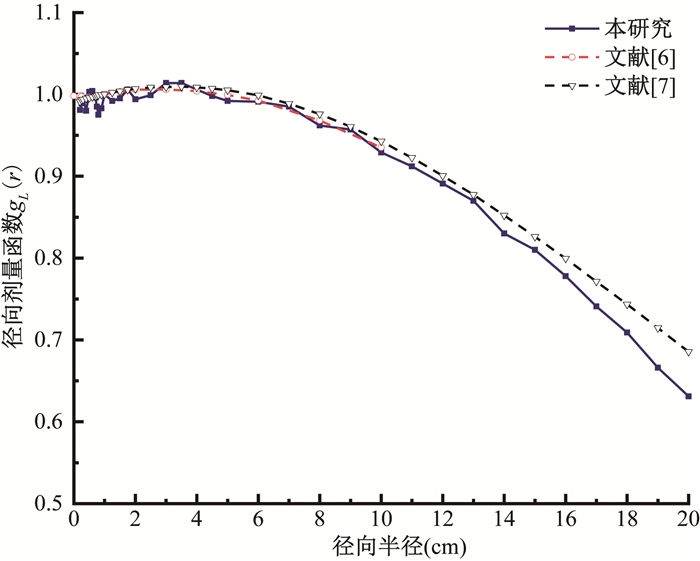
2.径向剂量函数：将模拟计算得出的数据代入公式(3)，得出了描述只考虑介质吸收和散射情况下，沿着放射源横轴垂直方向随距离增长，剂量率降低之比的径向剂量函数。图 3给出了本研究的径向剂量函数与文献研究数据的对比情况。本研究结果与文献[6-7]报道基本重合：在径向半径1 cm以内，径向剂量函数有一小波动，呈上升后下降的趋势；当径向半径 < 5 cm，所有研究结果显示铱源的径向剂量函数近似保持不变；当径向半径超过5 cm，径向剂量函数逐渐下降。当径向半径超过12 cm后，本研究的径向函数与文献[7]结果差异逐渐增大。考虑到女性盆腔厚度一般在30 cm以内，在径向半径15 cm处，本研究与文献报道的最大差异约为1.96%。

图 3 本研究和文献报道的径向剂量函数对比图 Figure 3 Comparison of radial dose functions between this study and references

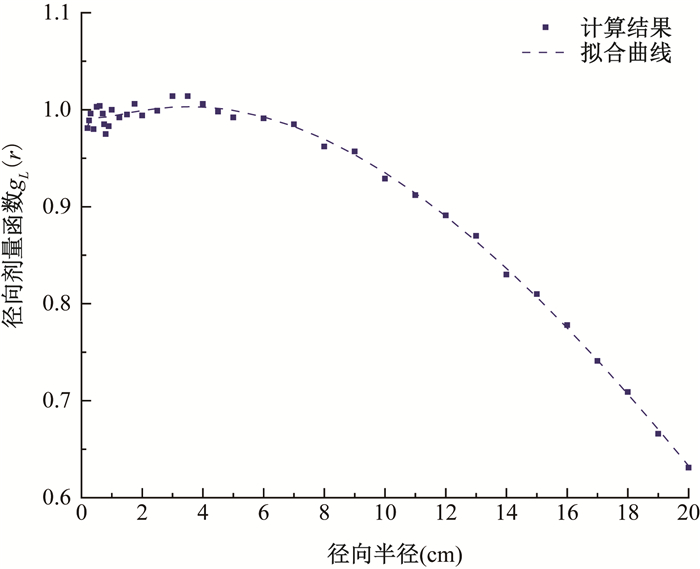
根据研究所得数据并运用Matlab cftool工具箱对径向剂量函数数据进行拟合(图 4)得到经验公式gL(r)=(a0×r－2+a1×r－1+a2+a3×r+a4×r2+a5×r3)×e(－a6×r)，当径向半径r < 20 cm时，式中系数a0、a1、a2、a3、a4、a5、a6分别为-0.001 42、0.008 40、0.973 44、0.034 67、-0.001 82、-4.888 33×10-8和0.019 72。

图 4 GammaMed Plus HDR 192Ir源的径向剂量函数拟合曲线 Figure 4 Fitting curve of radial dose function for GammaMed Plus HDR 192Ir source

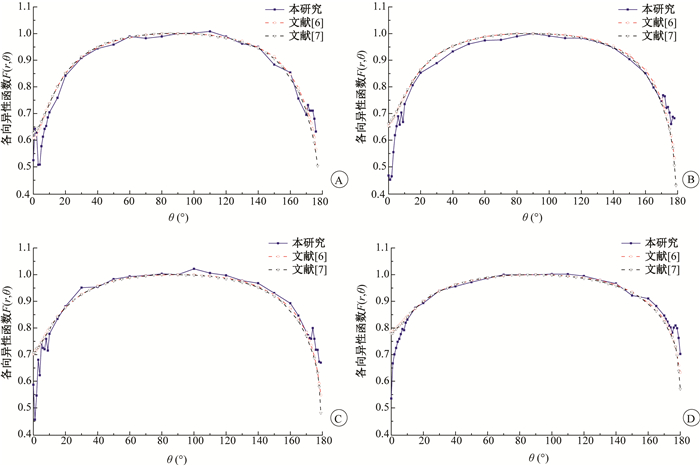
3.各向异性函数：如表 2所示，根据公式(4)可以得出各向异性函数，它是描述不考虑几何因素，在距源中心r，各方向θ上，介质吸收及散射效应对剂量率分布的影响。图 5分别给出了不同径向半径下，本研究和文献[6-7]报道的各向异性函数的对比情况。可见，在放射源的两端(0°及180°)，本研究与文献[6-7]的各向异性函数偏差较大；而在中垂线方向(90°)，该函数偏差相对较小。

表 2 距源中心不同距离的GammaMed Plus HDR 192Ir源的各向异性函数表 Table 2 Anisotropy function value at different radial distances for GammaMed Plus HDR 192Ir source

图 5 本研究和文献报道的距源中心不同距离的各向异性函数对比图    A.1 cm；B.3 cm；C.5 cm；D.10 cm Figure 5 Anisotropy functions at different radial distances in this study and literatures    A.1 cm; B.3 cm; C.5 cm; D10 cm.

讨论

AAPM TG43号[2]报告中提出了描述放射源剂量学特性的物理量，并给出常见放射源的剂量参数标准，而TG-43U1报告[5]又分别给出了利用蒙特卡罗计算及实验测量两种方法更新的相应参数的参考标准，同时建议在临床计划系统使用前需要再次确定这些剂量学参数，以保证近距离治疗剂量的精确性。由于采用实验方法对硬件要求多，测量精确难以保证，因此很多学者利用不同蒙特卡罗软件对放射源的剂量学参数进行模拟计算。如近年来加拿大研究人员Taylor和Rogers[7, 10]利用EGSnrc程序对多种放射源的剂量学参数展开了系统的研究，而Perez-Calatayud等[6]整理了近距离治疗常用的192Ir、137Cs和60Co的物理学参数的模拟计算值和测量值，其中包括Ballester等[11]利用GEANT3程序模拟计算了GammaMed 12i和Plus两种型号铱源的剂量学参数；王先良等[12]利用EGSnrc软件针对GZP型60Co剂量学参数进行分析，结果与Granero等[13]用GEANT4软件模拟的剂量率常数相差仅1%。曹振等[14]为了验证MCNP5软件和EGSnrc软件的计算精度，将两种软件对125I模拟结果与实验测量的剂量分布进行比较，得出EGSnrc剂量数据更准确的结论。可见，EGSnrc软件在放射源在介质中剂量分布的模拟计算具有较明显的优势。

本研究基于EGSnrc蒙特卡罗软件对GammaMed Plus HDR 192Ir源进行精细几何结构模型建立，分别利用FLURZnrc和DOSRZnrc子程序计算光子通量谱和水介质中吸收剂量。研究得出的单位活度空气比释动能强度、剂量率常数与文献[6-7]结果近似。而径向剂量函数与文献报道基本一致，在径向半径1 cm以内，有一“拐点”结构存在；之后随着径向半径增大，函数呈连续下降。同时，由于模拟中选用的水模体结构尺寸不同，加之坐标转换时采用的是双线性插值，而非文献中所用的线性插值，造成了当径向半径>12 cm后，本研究径向函数与文献[7]存在一定的差异。考虑到实际患者体厚，结合近距离治疗范围有限，剂量跌落快等特点，该差异对径向半径超过12 cm的低剂量处剂量计算影响非常小。此外，由于本研究模拟的放射源模型为矩形，而实际放射源为弧形端部，这种结构差异造成放射源端部吸收剂量的偏差，因此各向异性函数与两个国外研究团队的研究结果相比，在放射源端部位置有少量偏差。

总之，基于EGSnrc蒙卡软件的GammaMed Plus HDR 192Ir源剂量学特性研究是可行的，其计算结果与文献报道差距很小。本研究工作为临床近距离治疗计划系统的验收提供基础数据，是精确评价近距离放疗剂量的理论参考依据。而以此研究为基础，下一步计划对考虑施源器和非均匀组织影响的实际临床病例展开分析研究。

利益冲突 所有署名作者按以下贡献声明独立开展，未接受有关公司的任何赞助，不涉及各相关方的利益冲突
作者贡献声明 吴爱林负责构思、模拟计算、论文撰写；吴爱东，朱磊负责立意确认、论文修改；刘云琴、钱立庭协助研究、指导写作
参考文献
[1]
杜霄勐, 安菊生, 吴令英, 等. 宫颈癌近距离放射治疗新进展[J]. 癌症进展, 2015, 11(2): 152-158.
Du XY, An JS, Wu LY, et al. New progress in cervical cancer brachytherapy[J]. Oncol Prog, 2015, 11(2): 152-158. DOI:10.11877/j.issn.1672-1535.2015.13.02.09
[2]
吴爱林, 吴爱东, 刘云琴, 等. 宫颈癌二维近距离后装治疗中危及器官参考点剂量与三维体积剂量的相关性研究[J]. 中华放射医学与防护杂志, 2016, 36(11): 847-851.
Wu AL, W AD, Liu YQ, et al. Study of association between OARs reference points doses and OARs 3D volume doses in 2D intracavitary brachytherapy for cervical cancer[J]. Chin J Radiol Med Prot, 2016, 36(11): 847-851. DOI:10.3760/cma.j.issn.0254-5098.2016.11.010
[3]
Li Z, Das RK, DeWerd LA, et al. Dosimetric prerequisites for routine clinical use of photon emitting brachytherapy sources with average energy higher than 50 keV[J]. Med Phys, 2007, 34(1): 37-40. DOI:10.1118/1.2388155
[4]
Nath R, Anderson LL, Luxton G, et al. Dosimetry of interstitial brachytherapy sources:recommendations of the AAPM Radiation Therapy Committee Task Group No. 43. American Association of Physicists in Medicine[J]. Med Phys, 1995, 22(2): 209-234. DOI:10.1118/1.597458
[5]
Rivard MJ, Coursey BM, DeWerd LA, et al. Update of AAPM Task Group No. 43 report:A revised AAPM protocol for brachytherapy dose calculations[J]. Med Phys, 2004, 31(3): 633-674. DOI:10.1118/1.1646040
[6]
Perez-Calatayud J, Ballester F, Das RK, et al. Dose calculation for photon-emitting brachytherapy sources with average energy higher than 50 keV:report of the AAPM and ESTRO[J]. Med Phys, 2012, 39(5): 2904-2929. DOI:10.1118/1.3703892
[7]
Taylor RE, Rogers DW. An EGSnrc Monte Carlo-calculated database of TG-43 parameters[J]. Med Phys, 2008, 35(9): 4228-4241. DOI:10.1118/1.2965360
[8]
Kawrakow I, Mainegra-Hing E, Rogers DW, et al. The EGSnrc code system: Monte Carlo simulation of electron and photon transport[M/OL]. Ottawa: National Research Council Canada, 2018. http://nrc-cnrc.github.io/EGSnrc/doc/pirs701-egsnrc.pdf.
[9]
Borg J, Rogers DW. Spectra and air-kerma strength for encapsulated 192Ir sources[J]. Med Phys, 1999, 26(11): 2441-2444. DOI:10.1118/1.598763
[10]
Taylor RE, Rogers DW. EGSnrc Monte Carlo calculated dosimetry parameters for 192Ir and 169Yb brachytherapy sources[J]. Med Phys, 2008, 35(11): 4933-4944. DOI:10.1118/1.2987676
[11]
Ballester F, Puchades V, Lluch JL, et al. Technical note:Monte-Carlo dosimetry of the HDR 12i and Plus 192Ir sources[J]. Med Phys, 2001, 28(12): 2586-2591. DOI:10.1118/1.1420398
[12]
王先良, 袁珂, 唐斌, 等. GZP型60Co源剂量学参数的蒙特卡洛模拟[J]. 中华放射肿瘤学杂志, 2016, 25(5): 489-495.
Wang XL, Yuan K, Tang B, et al. Brachytherapy 60Co source Dosimetric parameters Monte Carlo simulation[J]. Chin J Radiat Oncol, 2016, 25(5): 489-495. DOI:10.3760/cma.j.issn.1004-4221.2016.05.015
[13]
Granero D, Pérez-Calatayud J, Ballester F. Technical note:Dosimetric study of a new Co-60 source used in brachytherapy[J]. Med Phys, 2007, 34(9): 3485-3488. DOI:10.1118/1.2759602
[14]
曹振, 孟贝蒂, 张文在, 等. 复合型种子源125I-103Pd剂量场分布的蒙特卡罗模拟与实验测定[J]. 同位素, 2014, 27(2): 116-121.
Cao Z, Meng BD, Zhang WZ, et al. Determination of dose field distribution of 125I-103pd seed source with Monte-Carlo and experimental method[J]. J Isotopes, 2014, 27(2): 116-121. DOI:10.7538/tws.2014.27.02.0116