目前以电子射野影像装置(EPID)为代表的二维图形配准技术在临床上有着很大的应用[1-2],但无论是基于图像灰度的配准,还是基于骨性结构的配准,主要是以刚性配准的方式来实现。刚性配准的前提是假定两幅图像完全相同,只是在几何位置上存在偏差,经过平移和旋转变换后,两幅图像能够完全重合[3]。但在实际治疗过程中,患者的旋转和平移误差会导致相应方向投影的变化,导致投影图像与基准图像不再完全相同,并且随着偏差角度或偏移距离的增大,两幅图像的差别将会越来越大,如果还用刚性配准,将会降低配准结果的精度[4]。本研究考虑通过仿真头部体模模拟摆位误差,研究摆位误差引起的投影形变并提出改进配准方法。
材料与方法1.摆位误差引起的投影形变:物体的旋转和平移会导致投影的变化,本研究通过互信息来衡量投影的变化。互信息是一种衡量两个随机变量统计相关性的测度,在图像处理中本研究将互信息作为判断两幅图像在空间位置上是否一致的指标[5]。由于普通的互信息会受到图像重叠区域差别的影响,本研究采用了改进的归一化互信息来反映摆位误差引起的投影变化程度,即NMI:
| ${\rm{NMI}}({\rm{A}},{\rm{B}}) = \frac{{H({\rm{A}}) + H({\rm{B}})}}{{H({\rm{A}},{\rm{B}})}}$ | (1) |
式中,H(A)和H(B)分别为图像A和B的熵,bits;H(A,B)为图像A、B的联合熵[6]。
当两幅图像在空间上完全相同时,对应的归一化互信息值应为最大;相反如果两幅图像空间上变化越大,归一化互信息就越小。
本研究使用四川大学研制的仿真头部体模来代替真实患者,在体模的内部包含一具用高磷、高钙树脂制成的高仿真人工颅骨[7]。首先,在模拟定位机上设置仿真头部体模的等中心,然后在美国瓦里安公司的IX加速器上摆位,并借助瓦里安自带的PV aS1000 EPID拍摄正位图像,将其作为基准参考图像。分别使用精度为1 mm的钢尺沿z轴(上下)方向在-20~20 mm范围内、以1 mm为步长设置40例平移误差,以及使用精度为0.05°的角度仪绕x轴(左右)在-10°~10°范围内、以1°为步长设置20例旋转误差,拍摄上述设置的60例位置误差的正位EPID图像作为浮动图像,计算参考图像和浮动图像的互信息。本研究通过归一化互信息值的大小来反映摆位误差产生的投影变化程度。
2.改进配准算法:目前临床上主要使用EPID自带的基于灰度的刚性互信息配准软件来实现对二维图像的配准。共有3个配准参数:图像x方向的平移和图像y方向的平移、绕图像中心点的旋转[8]。如果摆位误差会导致投影图像发生变化,与参考图像不再完全一样,那么仅仅通过平移和旋转等刚性变换,已无法将两幅图像完全匹配,这时就需要形变配准(也称为非刚性配准)。但目前形变配准更多应用于三维图像配准[5, 9-10],二维图像的形变配准较少报道[11],原因是二维图像中人体的所有解剖信息是完全叠加在一起的。因此,在对比两幅图像时,很难精确的找到对应的解剖信息。
由于互信息配准算法具有较强的鲁棒性[12],并且通过分析侧位图像可知,当物体A绕轴旋转,或向下平移时,投影会呈现出一种近似缩放的改变(图 1),平移和旋转导致的投影变化可以在一定程度上看成投影在图像x、y两个方向上的缩放,本研究在原有3个配准参数的基础上再增加2个配准参数,分别是图像x方向和y方向的缩放比例,通过对两个缩放比例的优化来校正平移和旋转引起的投影图像形变,所以本研究的配准方法一共有5个配准参数。在优化算法上,本研究采取粒子群优化算法(particle swarm optimization,PSO)和鲍威尔(Powell)优化算法结合的改进型混合优化算法[13],以兼顾全局优化搜索能力强和局部优化收敛速度快的优点。
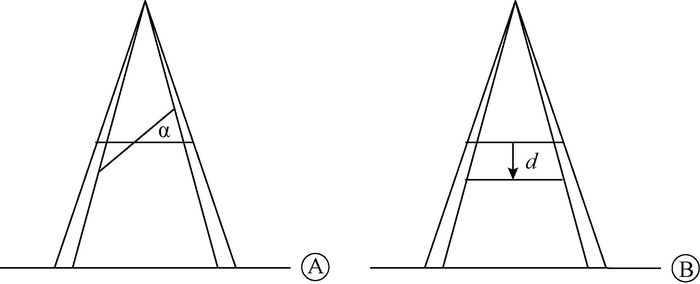
|
图 1 旋转和平移导致的投影变化A.旋转;B.平移 注:α为物体绕轴旋转角度,d为物体向下平移距离 Figure 1 Transformation of projection with translation and rotation A. Rotation; B.Translation |
3.配准结果分析方法:使用精度为1 mm的钢尺设置头部体模的平移误差,通过精度为0.05°的角度仪测量头部体模底座上的水平基准线,借助底部填塞纸片来设置旋转误差,拍摄正侧位EPID图像,分别运用目前临床上使用的传统互信息配准方法和本研究的改进配准算法进行配准。体模x轴(左右)的平移误差取自正位图像x(水平)方向的偏差,y轴(头脚)的平移误差取自正位图像y(垂直)方向偏差和侧位图像y方向偏差的平均值,z轴(上下)的平移误差取自侧位图像x方向的偏差,绕x轴的旋转误差取自侧位图像绕图像中心点的旋转误差,绕z轴的旋转误差取自正位图像绕图像中心点的旋转误差。将得到的摆位误差结果与实际摆位误差进行比较,以判断本研究的改进算法相对于目前临床使用的传统配准方法的优劣。
由于EPID无法检测出绕y轴方向的旋转误差,所以只设置了体模x、y、z轴的平移误差和绕x、z轴的旋转误差。根据临床中可能出现的摆位误差范围设置20例摆位误差,以3 mm平移误差和3°旋转误差为界,分为较小摆位误差组和较大摆位误差组,每组各10例(表 1,2)。
|
|
表 1 较小摆位误差设置(平移误差≤3 mm,旋转误差≤3°) Table 1 The parameters of the ten cases with smaller errors (translation error≤3 mm, rotation error≤3°) |
|
|
表 2 较大摆位误差设置(平移误差≥3 mm,旋转误差≥3°) Table 2 The parameters of the ten cases with larger errors (translation error≥3 mm, rotation error≥3°) |
4.软件实现及统计学处理:通过Matlab R2008a软件自编配准软件,实现本研究的改进互信息配准算法。采用SPSS 16.0软件对设置的20例模拟摆位误差实验结果进行配对t检验,P<0.05为差异有统计学意义。
结果1.投影图像的变化程度:仿真头部体模分别绕轴旋转、沿射束方向平移导致的归一化互信息变化示于图 2,3。随着仿真体模旋转角度或平移距离的增大,其互信息值相对于基准位置互信息的差别呈现不断扩大的趋势,表明此时的投影图像的变化越发显著。头部体模在旋转误差为-10°和10°时,较基准位置的互信息值分别减少了10.2%和10.0%;而头部体模在平移误差为-20 mm和20 mm时,较基准位置的互信息值甚至减少了34.1%和32.4%。如果用此时的投影图像与基准位置图像进行互信息配准,必然会导致较大的误差。
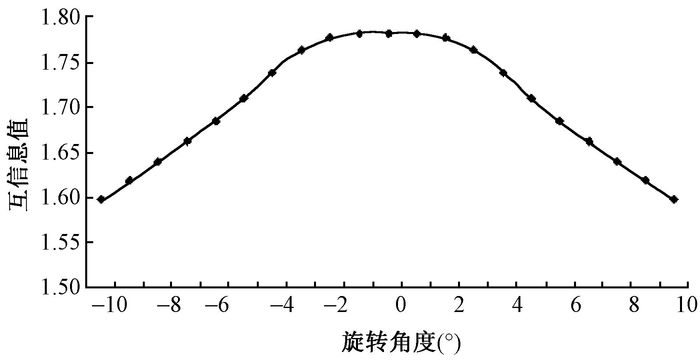
|
图 2 旋转导致的互信息变化 Figure 2 The mutual information value with rotation |
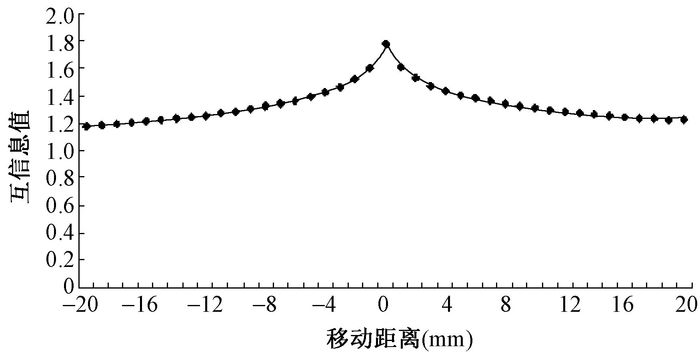
|
图 3 平移导致的互信息变化 Figure 3 The mutual information value with translation |
2.不同方法配准耗时的比较:使用传统互信息配准方法和本研究改进的互信息配准方法分别对较小摆位误差组和较大摆位误差组进行配准的耗时见表 3。从实验结果可以看到,无论是对于较小摆位误差组还是较大摆位误差组,改进互信息方法的配准耗时会比加速器自带的互信息(以下简称互信息)方法延长,平均耗时分别达到31.1和33.2 s,但也在临床可接受范围内。
|
|
表 3 较小摆位误差组和较大摆位误差组不同配准方法的配准耗时比较(s) Table 3 Comparison of the average registration time between the two methods for the cases with smaller errors and bigger errors(s) |
3.不同方法配准精度的比较:使用传统互信息方法和改进的互信息方法分别对较小摆位误差组和较大摆位误差组进行配准的结果分别见图 4,5。通过观察分区迭加的配准融合图像上两幅图像交界处解剖结构轮廓连接的平滑程度可以看到,对于较小摆位误差组,互信息方法和改进的互信息方法都可以准确配准两幅图像;而对于较大摆位误差组,改进的互信息方法的精度依旧较高,但互信息方法却出现了较大的配准误差,如图 5A红色箭头所示。
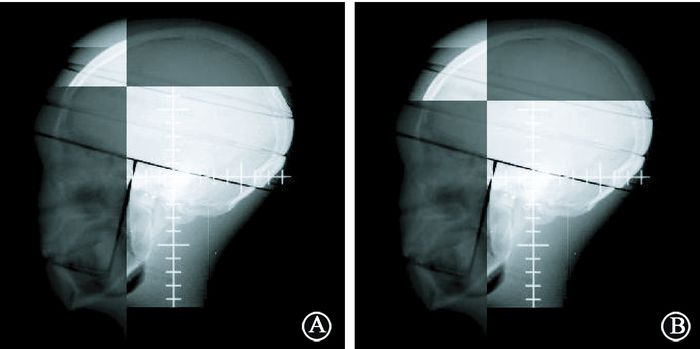
|
图 4 较小摆位误差组不同配准方法的配准结果比较 A.传统互信息;B.改进互信息 Figure 4 Comparison of the registration between the two methods for the cases with smaller errors A. Mutual information registration; B. Improved mutual information registration |
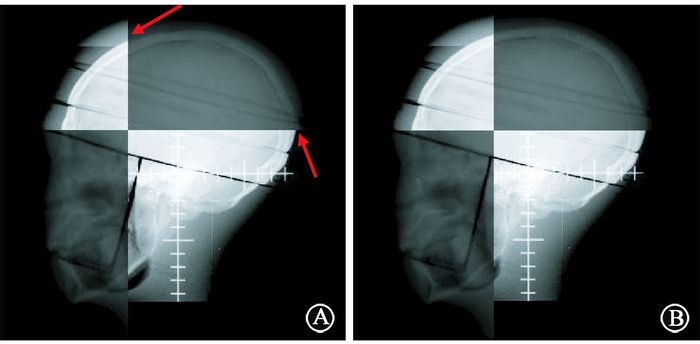
|
图 5 较大摆位误差组不同配准方法的配准结果比较A.传统互信息;B.改进互信息 注:红色箭头表示较大误差 Figure 5 Comparison of the registration between the two methods for the cases with larger error A. Mutual information registration; B. Improved mutual information registration |
对不同配准方法精度进行量化分析也印证了上述观察结果,量化分析的结果列于表 4,5。对于较小摆位误差组,互信息方法和本研究的改进互信息方法在精度上差异没有统计学意义,但对于较大摆位误差组,两种方法的精度差异有统计学意义(t=4.386、3.160、2.845、3.048、2.621, P<0.05),本研究改进互信息方法精度优于互信息方法。
|
|
表 4 较小摆位误差组不同配准方法的配准精度量化比较(mm/°) Table 4 Quantitative comparison of the registration accuracy between the two methods for the cases with smaller error(mm/°) |
|
|
表 5 较大摆位误差组不同配准方法的配准精度量化比较(mm/°) Table 5 Quantitative comparison of the registration accuracy between the two methods for the cases with larger error(mm/°) |
讨论
EPID使用时间长,配置费用经济,所以目前在我国的各级医院中作为一种图像引导放疗技术(IGRT)的实现方式仍在广泛使用[14]。目前,临床上使用的EPID配准方式主要有两种,分别是基于特定骨性结构或者植入标记物的手工配准和基于传统互信息的配准方法。手工配准方法操作繁琐,并且过多的人工干预使得验证效率低下,同时增加了结果的不确定性,因此临床上更多的是使用传统互信息配准方法。
相对于与基于标记的配准方法,基于传统互信息的配准方法具有更高的配准精度[15],但本研究发现,传统互信息方法的配准准确性会随摆位误差的增大而降低。在摆位误差较小的实例中,传统互信息配准方法的精度较高,但在摆位误差较大的实例中,x、y、z轴平均平移误差分别升高到0.9、0.7和0.8 mm,x、z轴平均旋转误差分别升高到0.9°和0.8°。
本研究分析导致摆位误差较大时,传统互信息配准误差也较大的原因,除了与配准所采用的最优化算法的全局搜索能力相关外,还与投影形变的影响有关。因为摆位误差越大,投影变化也会越显著,作为刚性配准技术的传统互信息配准方法必然会产生不同程度的配准误差[16-17]。对此,本研究改进优化算法的全局搜索能力,解决当优化初始值离全局最优值较远时,优化算法局部收敛的问题,但克服投影变化的影响只能通过形变配准实现。EPID二维图像中人体的所有解剖信息完全叠加在一起,在两幅图像中找到对应的解剖信息,进行形变配准带来了极大的困难,因此本研究增加图像x、y方向上的缩放比例两个参数,优化这两个参数校正形变对配准的影响,虽然这种近似的形变校正只能对人体图像的整体进行校正,还无法达到对每一个解剖点进行形变配准,但这种不足是由二维图像自身的局限性决定的,相对于原有的二维互信息刚性配准方法来说,已经是一种改进。
本研究通过摆位误差模拟实验可以看到,对于摆位误差较小的实例,本研究的改进互信息配准算法的精度也较高,和传统互信息方法的配准精度差异没有统计学意义,但当摆位误差较大时,本研究的改进互信息方法平均配准误差较互信息方法分别下降55.6%、57.1%、62.5%、66.7%和62.5%,差异具有统计学意义,说明在摆位偏差较大时,本研究的改进互信息方法能够提供更高的配准精度, 而在患者的实际照射过程中,这种较大的摆位误差是可能出现的。徐鹭英等[18]分析了30例头颈部肿瘤患者的摆位误差,发现患者在左右、上下、前后方向的最大平移误差分别达到6.0、4.6和4.9 mm,最大旋转误差分别达到4.1°、4.1°和2.4°,Zeidan等[19]也发现,至少有>11%的头颈肿瘤患者治疗摆位误差>5 mm。虽然本研究改进方法的平均配准耗时会延长,但也在临床可接受范围内。
利益冲突 本研究由署名作者按以下贡献声明独立开展,未接受有关公司的任何赞助,不涉及各相关方的利益冲突作者贡献声明 陈诚负责论文的设计及撰写;鲍志荣负责数据收集;於海军协助统计分析;刘晖指导论文修改
| [1] |
邬筱莹, 章真, 王文超, 等. 电子射野影像装置对盆腔肿瘤放疗摆位误差的测定[J].
中华放射肿瘤学杂志, 2007, 16 (1): 52-54. Wu XY, Zhang Z, Wang WC, et al. Evaluation ofset-up errors in pelvic irradiation with electronic portal imaging device[J]. Chin J Radiat Oncol, 2007, 16 (1): 52-54. DOI:10.3760/cma.j.issn.1004-4221.2007.01.013. |
| [2] |
张彦新, 戴建荣, 易俊林, 等. 应用EPID分析头颈部肿瘤调强放疗的摆位误差[J].
中华放射肿瘤学杂志, 2008, 17 (1): 39-42. Zhang YX, Dai JR, Yi JL, et al. Analyzing setup error with electron portal images device for head and neck tumors treated with intensity modulated radiation therapy[J]. Chin J Radiat Oncol, 2008, 17 (1): 39-42. DOI:10.3760/cma.j.issn.1004-4221.2008.01.010. |
| [3] | Markelj P, Tomaževič D, Likar B, et al. A review of 3D/2D registration methods for image-guided interventions[J]. Med Image Anal, 2012, 16 (3): 642-661. DOI:10.1016/j.media.2010.03.005. |
| [4] | Tsao J. Interpolation artifacts in multimodality image registration based on maximization of mutual information[J]. IEEE Trans Med Imaging, 2003, 22 (7): 854-864. DOI:10.1109/TMI.2003.815077. |
| [5] | Loeckx D, Slagmolen P, Maes F, et al. Nonrigid image registration using conditional mutual information[J]. IEEE Trans Med Imaging, 2010, 29 (1): 19-29. DOI:10.1109/TMI.2009.2021843. |
| [6] |
杨志杰, 于明, 张海哲. 归一化互信息配准[J].
计算机与信息技术, 2005 (6): 18-22. Yang ZJ, Yu M, Zhang HZ. Image registration based on normalized mutual information[J]. Comput Inf Technol, 2005 (6): 18-22. |
| [7] |
高向涛, 林大全, 颜海婴, 等. 中国人仿真头颈部体模的解剖参数及CT值研究[J].
中华放射医学与防护杂志, 1998, 18 (6): 414-417. Gao XT, Lin DQ, Yan HY, et al. Dissection parameters and CT values of a Chinese head and neck pantom[J]. Chin J Radiol Med Prot, 1998, 18 (6): 414-417. DOI:10.3760/cma.j.issn.0254-5098.1998.06.017. |
| [8] | Viola P, Wells WM. Alignment by maximization of mutual information[J]. Int J Comput, 1997, 24 (2): 137-154. DOI:10.1109/ICCV.1995.466930. |
| [9] | Rivaz H, Collins DL. Near real-time robust non-rigid registration of volumetric ultrasound images for neurosurgery[J]. Ultrasound Med Biol, 2015, 41 (2): 574-587. DOI:10.1016/j.ultrasmedbio.2014.08.013. |
| [10] | Sotiras A, Davatzikos C, Paragios N. Deformable medical image registration: a survey[J]. IEEE Trans Med Imaging, 2013, 32 (7): 1153-1190. DOI:10.1109/TMI.2013.2265603. |
| [11] | Park T, Jung H, Yun ID. Nonrigid 2D registration of fluoroscopic coronary artery image sequence with layered motion[J]. Spie Med Imaging, 2016, 9788 DOI:10.1117/12.2218565. |
| [12] |
唱轶钲, 山世光, 高文, 等. Gabor特征判别分析人脸识别方法的误配准鲁棒性分析[J].
计算机工程与应用, 2005, 41 (5): 56-59. Chang YZ, Shan SG, Gao W, et al. Evaluation of Gabor features for face recognition from the angle of robustness to Mis-alignment[J]. Comput Eng Appl, 2005, 41 (5): 56-59. DOI:10.3321/j.issn:1002-8331.2005.05.020. |
| [13] |
陈诚, 黄劭敏, 邓小武, 等. 兆伏级放疗射野图像与模拟图像自动配准算法研究[J].
中华放射肿瘤学杂志, 2010, 19 (3): 256-260. Chen C, Huang SM, Deng XW, et al. Study on registration algorithm for portal images and simulation images in megavolt radiotherapy[J]. Chin J Radiat Oncol, 2010, 19 (3): 256-260. DOI:10.3760/cma.j.issn.1004-4221.2010.03.023. |
| [14] | Jaffray DA, Siewerdsen JH, Wong JW, et al. Flat-panel cone-beam computed tomography for image-guided radiation therapy[J]. Int J Radiat Oncol Biol Phys, 2002, 53 (5): 1337-1349. DOI:10.1016/S0360-3016(02)02884-5. |
| [15] | Kim J, Fessler JA, Lam KL, et al. A feasibility study of mutual information based setup error estimation for radiotherapy[J]. Med Phys, 2001, 28 (12): 2507-2517. DOI:10.1118/1.1420395. |
| [16] | Kun H, Menglong H, Chenkai Y. An action-space-based global optimization algorithm for packing circles into a square container[J]. Comput Oper Res, 2015, 58 (C): 67-74. DOI:10.1016/j.cor.2014.12.010. |
| [17] | Wang CF, Liu K. A novel particle swarm optimization algorithm for global optimization[J]. Comput Intell Neurosci, 2016, 2016 (7): 1-9. DOI:10.1155/2016/9482073. |
| [18] |
徐鹭英, 潘建基, 王笑良, 等. 头颈部肿瘤图像引导调强放疗中摆位误差对剂量学的影响研究[J].
中华放射肿瘤学杂志, 2011, 20 (6): 506-509. Xu LY, Pan JJ, Wang XL, et al. The preliminary study of setup error's impact on dose distribution of image guide radiation therapy for head and neck cancer[J]. Chin J Radiat Oncol, 2011, 20 (6): 506-509. DOI:10.3760/cma.j.issn.1004-4221.2011.06.017. |
| [19] | Zeidan OA, Langen KM, Meeks S, et al. Evalution of image-guidance protocols in the treatment of head and neck cancers[J]. Int J Radiat Oncol Biol Phys, 2007, 67 (3): 670-677. DOI:10.1016/j.ijrobp.2006.09.040. |
 2017, Vol. 37
2017, Vol. 37


