目前临床已普遍开展了调强放疗技术 (intensity modulated radiation therapy, IMRT),其剂量计算模型主要采用叠加/卷积算法和笔射束算法[1]。然而,这些计算模型在小野照射,存在腔体的区域及非均匀组织中剂量计算并不准确[2],因此,在治疗前必须进行剂量验证。目前IMRT剂量验证方法,主要以模体代替患者利用二维平面探测器矩阵和三维均匀模体进行测量验证,将测量结果与治疗计划系统 (treatment planning system,TPS) 结果进行比较。该方法能准确评估TPS在模体中剂量算法的偏差,具有一定的可靠性。但对于复杂的人体,无法测量其肿瘤靶区和危及器官的剂量分布情况,使得临床剂量验证的实际意义受到很大限制[3]。蒙特卡罗 (Monte Carlo,MC) 算法是模拟每个光子和电子在物质中的输运和能量沉积过程,是目前最准确的剂量计算方法[4],对于组织具有低密度性或非均匀性等常规剂量计算方法难以保证计算精度的情形,更可体现其优越性。
本研究借助开源蒙特卡罗程序包EGS4/BEAM的基础上进行进一步完善,使其具备用于临床剂量验证的功能。首先,比较所模拟结果与测量结果分别在三维水箱和二维平面探测矩阵体模 (multicube) 中的差异,验证模拟过程及计算结果的准确性;最终利用患者的CT数据与TPS设计的加速器几何信息进行MC剂量再计算,比较所计算结果与Pinnacle自带剂量筒串卷积算法 (collapsed cone convolution,CCC) 在鼻咽癌真实病例中的差异,实现临床IMRT计划三维剂量验证,说明使用MC方法进行剂量验证具有较好的临床意义。
一、 材料与方法主要利用BEAMnrc,DOXYZnrc蒙特卡罗程序对美国瓦里安公司23EX加速器6 MV X射线放射源进行模拟和模体剂量计算。该程序是由加拿大国家研究院中心组在EGS4基础上开发的OMEGA项目,是一种通用的MC吸收剂量计算程序。在此基础上,本研究实现了放疗计划到MC剂量计算的解析、计算结果的剂量分析,以及图像显示等功能。同时,该系统还可对计算结果进行γ通过率对比,剂量体积直方图 (dose volume histograms,DVH) 比较以及三维图像剂量分布显示等方式的评估。
1.蒙特卡罗模拟:用BEAMnrc蒙特卡罗程序对加速器机头的组件进行准确建模。其中将加速器建模分为放射源相空间建模 (up-head) 和准直器建模 (down-head) 两部分。放射源相空间建模包括靶、初级准直器、Be窗、均整器、电离室和射野镜。准直器建模包括二级准直器 (JAWs),多叶光栅 (MLC) 等。将BEAMnrc模拟放射源相空间生成的相空间数据作为准直器模拟的输入源。为了实现调强剂量计算,二级准直器和多叶光栅选用具有同步功能的SYNCJAWS,SYNCVMLC组件,分别导入JAWs文件和MLC文件,实现与DOSXYZnrc程序对模体进行三维任意方向的多角度同步模拟计算。放射源分别选择高斯分布的放射源和相空间文件输入的放射源。电子从真空加速管射出电子窗时,电子束为单能单向的,能量选择6 MeV,束流半径为0.13 cm,电子束方向为 (0,0,1)。为了提高计算效率,减少统计误差,需要对电子截止能量、光子截止能量及韧致辐射粒子分裂数等主要模拟参数进行优化设置[5],截止能量ECUT=0.70 MeV,PCUT=0.01 MeV。
在DOSXYZnrc程序对模体进行剂量计算过程中,选择具有同步功能的放射源。将准直器部分建立的放射源模型与模体的剂量计算部分进行同步模拟运算,完成不同机架角度的调强剂量计算。蒙特卡罗模拟的不确定度和模拟时间受模拟粒子数量,体素大小与数量,射野大小及子野多少的影响[6],为使计算结果在兴趣区不确定度小于2%,本文将模拟粒子数设置为1×108~1×1010,模拟时间约为2~80 h。最后,所用的计算机平台为Intel i7-6700k@4 GHz处理器,8 Gb内存,Linux Fedora 20操作系统。
2.治疗计划的提取:从Pinnacle 9.6计划系统获取完成的放射治疗计划数据,导出DICOM数据文件:包括CT图像文件,计划文件RP,剂量文件RD,靶区勾画结构文件RS。运用MATLAB编程实现数据文件转换,用于MC模拟及剂量分析对比。TPS采用CCC进行剂量计算,网格大小设为3 mm。本研究采用2例鼻咽癌9野调强放射治疗计划,为减少小野剂量的差异[7],将最小子野设置为5 cm×5 cm。
3.剂量计算与测量验证
(1) 一维剂量验证:使用Blue Phantom三维剂量测量系统。将三维水箱放于SSD=100 cm处,进行探测器中心点校准后,开始测量。在相同条件下建立MC模拟模型,水模体体素设置为2 mm×2 mm×2 mm,计算不同方野在水中的剂量分布。取射野中心轴的百分深度剂量 (percentage depth dose, PDD) 和水下任意深度的射野离轴比 (off-axis ratio, OAR),分别将结果进行归一化处理。分析比较测量值与计算值,对建立的MC加速器模型进行初步验证。
(2) 二维平面剂量验证:使用IBA公司的二维平面矩阵电离室MatriXX。通过CT扫描获取MatriXX定制配套模体Multicube (IBA Dosimetry) 的CT数据,TPS和MC使用该数据进行剂量计算。首先,通过TPS设置5个不规则适形射野进行剂量计算,导出该结果进行测量和MC计算,将结果按TPS计划最大值进行归一化处理,比较三者之间的差异,对MC建立的准直器模型在不规则射野中的走位精度进行验证。其次,将病例中的9野IMRT计划机架归为0°,对Matrixx模体制定TPS验证计划,完成计划测量和MC计算。最后,将获取的测量平面剂量分布数据,进行剂量分布曲线对比及γ分析,完成IMRT的二维平面验证。
(3) 三维患者剂量验证:将鼻咽癌IMRT计划和患者CT数据导入MC进行计算。将MC计算结果按TPS最大值进行归一化处理,比较分析患者三维组织结构的剂量分布,对比DVH差别,评估放射治疗计划。
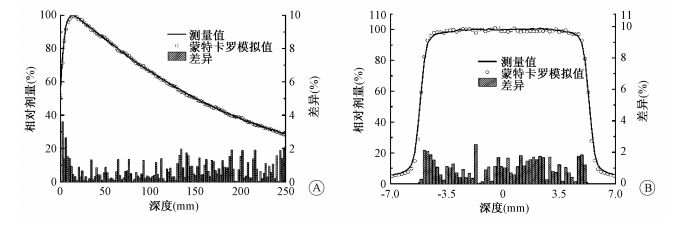
二、 结果1.与点剂量测量的PDD和OAR比较:图 1是射野为10 cm×10 cm,在射野中心轴PDD (图 1 A) 和深度为5 cm的OAR (图 1 B) 测量值与MC模拟的比较结果,测量值与计算值分别在剂量最大处进行归一化处理。由图 1可见,在最大剂量点深度以下和射野平坦区二者差异不明显,误差均在2%以内,低于精确放疗中计划系统剂量计算的允许误差3%[8]。但是,由图也不难发现在剂量建成区域和半影区剂量计算值和测量值差异较大,这主要与网格大小及电离室本身的固有特性和侧向电子失衡有关。其他射野的PDD和OAR计算与测量结果与此类似。
|
图 1 10 cm×10 cm过射野中心轴相对剂量曲线与相对差异 A.百分深度剂量与差异;B.水下5 cm射野离轴比与差异 Figure 1 Relative dose curve and differences along beam center axis for 10 cm×10 cm field A. Percentage depth dose and difference; B. Off-axis ratio at underwater 5 cm and difference |
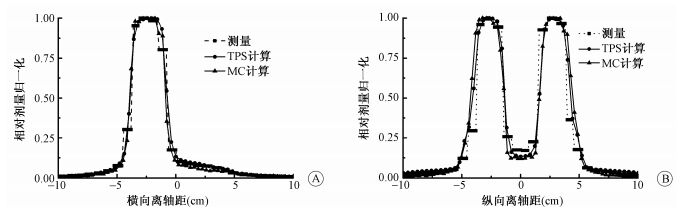
2.在二维平面剂量验证中的比较:图 2为一不规则横向U形适形射野在MatriXX模体测量平面过等中心横向与纵向剂量离轴比。由图 2可见,在横向和纵向三者的离轴比具有良好的一致性,仅在半影区域存在一定的差异。其他适形射野的结果与此类似。通过比较各适形射野MC、TPS与MatriXX三者之间的γ通过率,按3 mm 3%的标准,三者比较的结果γ通过率≤1均好于98%。
|
图 2 为侧向U形射野过中心点横向与纵向的剂量离轴曲线 A.横向离轴曲线;B.纵向离轴曲线 Figure 2 Profiles from isocentre along both horizontal and vertical axis for side-direction U field A. Profile along horizontal axis; B. Profile along vertical axis |
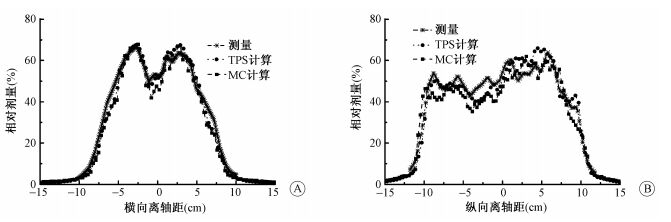
在对鼻咽癌患者的IMRT剂量验证中,首先利用TPS计算其在MatriXX模体中的平面剂量分布。再分别利用MatriXX测量加速器执行的计划数据以及MC计算模体中的剂量分布。图 3是病例1 TPS和MC在测量平面过中心点的横向和纵向的剂量离轴比。比较三者的γ通过率,按3 mm 3%的标准,MatriXX验证TPS的剂量γ通过率≤1为95.72%,MatriXX对MC的剂量γ通过率≤1为96.37%,MC对TPS的剂量γ通过率≤1为90.15%。MatriXX为实际测量值,测量验证MC的通过率比TPS计算稍高,MC验证TPS的通过率偏低。由图 3可见,在横轴方向剂量差异较小,在纵轴方向差异较大,差异较大的区域均为中心纵轴方向,这与在鼻咽癌调强放射治疗在解剖结构腔体部位相对应,估计与TPS在该部位进行优化过程中进行复杂的小野计算有关[9]。病例2验证结果与剂量分布规律与此类似,三者γ通过率≤1大于88%。MC验证的结果与实际MatriXX测量验证的结果具有很好的一致性。
|
图 3 IMRT验证计划在MatriXX模体中过中心点的横向与纵向剂量离轴曲线比较 A.横向剂量离轴曲线;B.纵向剂量离轴曲线 Figure 3 Profiles from isocentre along both horizontal and vertical axis for IMRT verification plan of MatriXX phantom A. Profile along horizontal axis; B. Profile along vertical axis |
|
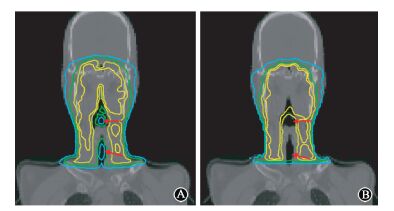
图 4 MC与TPS冠状位剂量分布与比较 A.MC计算;B.TPS计算 Figure 4 Comparison of dose distribution of coronal view given by both MC simulation and TPS calculation A. MC simulated result; B. TPS calculated result |
3.患者剂量验证:图 4为病例1鼻咽癌9野IMRT的冠状面MC和Pinnacle计划系统CCC算法等剂量分布曲线图,图中由内向外分别为80%(59 Gy)、70%(52 Gy)、50%(37 Gy)、30%(22 Gy) 等剂量分布曲线。其中,左侧为蒙特卡罗方法计算的等剂量分布曲线,右侧为CCC算法等剂量分布曲线,图中箭头指示的空腔部位可以显著看到蒙特卡罗模拟计算具有低剂量分布,CCC算法对于存在腔体中的结构高估了其剂量[10],这主要的原因是CCC算法对待组织中的腔体作为低密度水来处理进行剂量计算[11]。
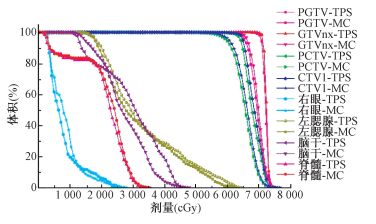
|
图 5 鼻咽癌MC和TPS计算剂量体积直方图比较 Figure 5 Comparison of DVH between MC simulation and TPS calculation for NPC |
图 5为该病例1鼻咽癌剂量体积直方图的比较,表 1为临床靶区 (CTV) 在TPS和MC算法的最大和平均剂量以及体积剂量与差异。由DVH图可看出在主要的靶区均存在不同程度的差异,其中CTV在最大剂量 (Dmax) 平均相差为0.36%(0.28 Gy),中位剂量平均差异达7.68%(5.06 Gy),体积剂量D95%(剂量覆盖95%的体积) 平均相差6.69%(4.22 Gy),体积剂量D50%平均相差3.90%(2.63 Gy),体积剂量D5%平均相差2.49%(1.79 Gy)。MC模拟结果存在较低的低剂量,估计这与靶区包括空腔组织在内相关,TPS高估了空腔中的剂量。由图 5也不难看出剂量计算在脑干的差异性较大,D50% MC计算比TPS低,相差约15%(约4 Gy),估计这与CCC算法比MC在低密度组织中具有更高的剂量[12],脑干位于高密度颅骨区间相关。其余危及器官的差异不明显。
|
|
表 1 CTV在TPS和MC算法的最大剂量和平均剂量以及体积剂量与相对差异 (Gy) Table 1 Comparison of mean, maximum and volume dose values for the treatment planning system (TPS) calculations and MC simulation results in the CTV volumes (Gy) |
三、 讨论
蒙特卡罗作为剂量计算的金标准,其准确性已被普遍认可,但由于运算效率较低,在过去较长时间限制了其临床的应用。本研究通过二步法避免了粒子在准直器以上部分重复进行模拟计算,大幅度提高计算效率。在此基础上,通过多CPU的并行运算使计算效率获得了数倍的提高,已完成初步实验,一定程度上满足了临床剂量验证的时间要求,下一步将进行验证研究。基于图像处理器 (graphics processing unit, GPU) 加速的应用已成为当前的研究热点,其计算速度获得突破性的提高满足于临床剂量计算的时间需求,并已应用于临床[13],未来将作为本研究进一步的研究方向。
本研究建立的MC剂量验证平台,与三维水箱在PDD与OAR测量比较,差异小于2%, 说明该MC模型能真实反映加速器实际治疗的剂量分布特性。对9野鼻咽癌计划MC模拟结果与MatriXX测量结果进行比较,MC模拟的结果与测量结果具有很好的一致性。在对两例鼻咽癌患者的调强放疗计划的MC剂量验证中,发现存在腔体与非均匀组织区域,MC模拟的结果低于TPS计算的剂量,CTV在TPS中其D95%更加优于MC模拟的结果,中位剂量偏差约7.6%(5.0 Gy)。本研究结果与相关研究结果相一致,陈华等[14]得出在空腔边缘筒串卷积算法 (CCC)、各向异性分析算法 (anisotropic analytical algorithm, AAA) 都高估了腔体剂量;Carrasco等[15]得出CCC算法在非均匀介质中比MC模拟具有更高的剂量,在骨水模体界面存在半影萎缩;Crowe等[16]通过MC模拟CCC计算的头颈部IMRT,得出在咽后壁结节与筛骨副鼻窦处中位剂量分别相差4.8%和6.7%,在主要的靶区中D95%均为CCC算法的结果优于MC模拟的结果。因此,在临床中计划系统对存在腔体与非均匀组织的靶区难以得到较为精确的剂量结果,针对以上情形病例,使用MC对其进行剂量验证,具有很好的临床意义。
本研究已初步建立MC验证平台能准确模拟加速器对患者进行三维剂量计算。但由于本研究使用的病例有限,剂量偏差无法成为临床指导的量化指标,今后将对临床的病例进行具体的分析。对今后应用MC模拟用于调强剂量验证具有很好的实际作用,尤其是在组织具有低密度性或非均匀性等常规剂量计算方法难以保证计算精度的情形,对靶区与危机器官三维剂量分布和评估,更可体现其优越性,具有很大的临床意义。
利益冲突 本研究全体作者无利益冲突, 未因进行该研究而接受任何不正当的职务或财务利益,在此对本研究的独立性和科学性予以保证作者贡献声明 杨耕负责程序模拟和撰写论文;王学涛、张白霖、招什武、朱远湖、朱琳负责计划的设计和实验测量;李飞、蔡春雅参与平台搭建、文献整理和数据处理;戴振晖负责研究思路指导、论文撰写指导与修改
| [1] | Cilla S, Digesù C, Macchia G, et al. Clinical implications of different calculation algorithms in breast radiotherapy: a comparison between pencil beam and collapsed cone convolution[J]. Phys Med, 2014, 30 (4): 473-481. DOI:10.1016/j.ejmp.2014.01.002. |
| [2] | Ezzell GA, Galvin JM, Low D, et al. Guidance document on delivery, treatment planning, and clinical implementation of IMRT: report of the IMRT Subcommittee of the AAPM Radiation Therapy Committee[J]. Med Phys, 2003, 30 (8): 2089-2115. DOI:10.1118/1.1591194. |
| [3] | Jursinic PA, Nelms BE. A 2-D diode array and analysis software for verification of intensity modulated radiation therapy delivery[J]. Med Phys, 2003, 30 (5): 870-879. DOI:10.1118/1.1567831. |
| [4] | Ahnesjö A, Aspradakis MM. Dose calculations for external photon beams in radiotherapy[J]. Phys Med Biol, 1999, 44 (11): R99-155. DOI:10.1088/0031-9155/44/11/201. |
| [5] | Keall PJ, Siebers JV, Libby B, et al. Determining the incident electron fluence for Monte Carlo-based photon treatment planning using a standard measured data set[J]. Med Phys, 2003, 30 (4): 574-582. DOI:10.1118/1.1561623. |
| [6] | Cygler JE, Daskalov GM, Chan GH, et al. Evaluation of the first commercial Monte Carlo dose calculation engine for electron beam treatment planning[J]. Med Phys, 2004, 31 (1): 142-153. DOI:10.1118/1.1633105. |
| [7] | Followill DS, Kry SF, Qin L, et al. The Radiological Physics Center's standard dataset for small field size output factors[J]. J Appl Clin Med Phys, 2012, 13 (5): 3962 DOI:10.1120/jacmp.v13i5.3962. |
| [8] | Jones D. ICRU report 50—prescribing, recording and reporting photon beam therapy[J]. Medical physics, 1994, 21 (6): 833-834. DOI:10.1118/1.597396. |
| [9] | Luo W, Meacham A, Xie X, et al. Monte Carlo dose verification for lung SBRT with CMS/XiO superposition algorithm[J]. Biomed Phys Eng Express, 2016, 2 (1): 015020 DOI:10.1088/2057-1976/2/1/015020. |
| [10] | Ma CM, Pawlicki T, Jiang SB, et al. Monte Carlo verification of IMRT dose distributions from a commercial treatment planning optimization system[J]. Phys Med Biol, 2000, 45 (9): 2483-2495. DOI:10.1088/0031-9155/45/9/303. |
| [11] | Seco J, Adams E, Bidmead M, et al. Head-and-neck IMRT treatments assessed with a Monte Carlo dose calculation engine[J]. Phys Med Biol, 2005, 50 (5): 817-830. DOI:10.1088/0031-9155/50/5/007. |
| [12] | Fogliata A, Vanetti E, Albers D, et al. On the dosimetric behaviour of photon dose calculation algorithms in the presence of simple geometric heterogeneities: comparison with Monte Carlo calculations[J]. Phys Med Biol, 2007, 52 (5): 1363-1385. DOI:10.1088/0031-9155/52/5/011. |
| [13] | Chi Y, Tian Z, Jia X. Modeling parameterized geometry in GPU-based Monte Carlo particle transport simulation for radiotherapy[J]. Phys Med Biol, 2016, 61 (15): 5851-5867. DOI:10.1088/0031-9155/61/15/5851. |
| [14] |
陈华, 徐义果, 庄志邈, 等. 放疗计划系统中空腔边缘剂量计算准确性研究[J].
中华放射肿瘤学杂志, 2017, 26 (1): 69-73. Chen H, Xu YG, Zhuang ZM, et al. Dose accuracy research on air cavity interface in treatment planning system[J]. Chin J Radiat Oncol, 2017, 26 (1): 69-73. DOI:10.3760/cma.j.issn.1004-4221.2017.01.016. |
| [15] | Carrasco P, Jornet N, Duch MA, et al. Comparison of dose calculation algorithms in phantoms with lung equivalent heterogeneities under conditions of lateral electronic disequilibrium[J]. Med Phys, 2004, 31 (10): 2899-2911. DOI:10.1118/1.1788932. |
| [16] | Crowe SB, Kairn T, Trapp JV, et al. Monte Carlo evaluation of collapsed-cone convolution calculations in head and neck radiotherapy treatment plans[C]//World Congress on Medical Physics and Biomedical Engineering May 26-31, 2012, Beijing, China. Springer Berlin Heidelberg, 2013: 1803-1806. DOI:10.1007/978-3-642-29305-4_474. |
 2017, Vol. 37
2017, Vol. 37


