非均整模式(FFF)由于去除均整器使射野内剂量分布不均匀,加之高剂量率的实现,在缩短患者治疗时间、 提高肿瘤治疗效率,降低辐射野外正常组织或器官的辐射损伤等方面,优于传统的均整模式(FF),这也为临床质量控制与质量保证工作带来了新的挑战[1-3]。本研究利用加拿大国家研究委员会(NRC)的BEAMnrc/DOSXYZnrc程序[4-5]建立6 MV FF和FFF模式加速器模型,参考Popescu等[6]方法,充分考虑次级准直器反射线对监测电离室的影响,分析次级准直器反射线和反射线占全部射线的比例与射野大小的关系,并通过计算射野输出因子建立各射野绝对剂量与机器跳数(MU)的对应关系,从而实现该模型的绝对剂量刻度,为医用直线加速器的X射线临床剂量学研究奠定模型与剂量传递基础。
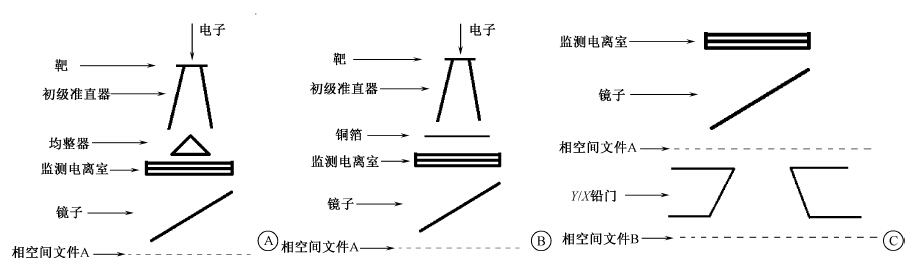
材料与方法1. 加速器机头模型及参数设置:考虑到x/y 轴的反射线对监测电离室剂量沉积的影响,设置两个蒙特卡罗模型如图 1所示。模型BEAM_up(包括FF和FFF两个模式)描述靶、 初级准直器、 均整器或铜箔、 监测电离室和反光镜等次级准直器以上恒定不变的组件部分,并在次级准直器上表面距离靶中心27.88 cm位置存储记录粒子的相空间文件A,用于BEAM_down部分模拟的输入源。BEAM_down模型模拟监测电离室、 反光镜和X/Y 铅门组件部分,并在X 铅门下表面记录粒子的相空间文件B。FFF模式的BEAM_up模型中,依据美国Varian公司提供的相关材料,在原均整器的位置设置一个厚度为0.812 6 cm的铜箔。
|
图 1 均整与非均整模式蒙特卡罗模型 A. BEAM_up 均整模型;B. BEAM_up 非均整模型; C.BEAM_down 模型 Figure 1 Monte Carlo models for FF and FFF A. BEAM_up FF model; B. BEAM_up FFFmodel; C. BEAM_down model |
本研究BEAM_up模型入射源设置为径向强度是高斯分布的圆形射束 (ISOURC 19号),入射电子束为高斯分布的6 MV单能,半高全宽(FWHM)为0.75 mm。电子输运截止能量(ECUT)和碰撞产生电子的最低能量(AE)设置为0.7 MeV,光子输运截止能量(PCUT)和韧致辐射产生光子的最低能量(AP)为0.01 MeV。为提高次级准直器反射线在监测电离室内剂量沉积的模拟精度,均整与FFF模式的BEAM_up模型产生相空间文件大小为56和48 G,分别包含3.097×109和1.842×109个粒子,作为BEAM_down模型的输入源。BEAM_down模型模拟粒子数设置为1.999×109~ 4.999×109,粒子数量与辐射野大小成正比,次级准直器反散在监测电离室的剂量沉积模拟结果不确定度控制在1%以内。
为了提高水模体中特定深度处的剂量计算精度,本研究选择SOURCE 9(机头BEAM模型)作为DOSXYZnrc程序输入源,这种共享程序库(shared library)的方式,避免了因相空间文件内粒子数较少而被重复使用所造成的非完全独立事件误差。DOSXYZnrc 程序使用50 cm ×50 cm ×50 cm标准水模体。其中,ECUT、 AE、 PCUT和AP参数与BEAMnrc程序相应参数设置相同。在计算射野中心轴上特定深度处剂量沉积时,对于4 cm×4 cm以下射野相应位置的体素设置为0.2 cm×0.2 cm×0.2 cm,其他射野设为半影区体素设置为0.5 cm×0.5 cm×0.5 cm,入射粒子数设置为2×109 ~6×1010,粒子数与射野大小成正比,计算结果的不确定度控制在<0.2%以内。
2. 绝对剂量刻度:依据加速器绝对剂量刻度规范,辐射野大小为10 cm× 10 cm,源靶距(SSD)为100 cm,在射野中心轴最大剂量点(Dmax)处,1 MU=1 cGy。MU为监测电离室的剂量单位,由监测到的比释动能转化而来,监测电离室的剂量沉积Dch计算如式(1)所示:
| ${D_{ch}} = D_{ch}^{forward} + D_{^{ch}}^{back}$ | (1) |
式中,Dchforward为单个电子从入射方向穿过监测电离室的剂量沉积;Dchback为X/Y铅门的反射线在监测电离室的剂量沉积。两个参数为监测电离室内空气部分剂量沉积的平均值,均可在BEAMnrc程序模拟的.egslst文件中获取,单位为Gy/粒子。
本研究用Dxyz表示在单个电子打靶后经过加速器机头各组件,最终在标准水模体中坐标为(x、 y、 z)处的体素(Voxel)所沉积的剂量,该数据存储在DOSXYZnrc程序所生成.3ddose文件中每个体素的剂量值,可以将指定数据输出到.egslst文件中,本研究使用matlab程序读取相关数据用于数据处理。而该体素的绝对剂量Dxyz,abs由式(2)给出:
| ${D_{xyz,}}abs = {D_{xyz}}{N_e}$ | (2) |
式中,Ne为入射粒子数或打靶粒子数,Ne个入射电子在监测电离室所沉积的绝对剂量Dch,abs表示如下:
| ${D_{ch,abs}} = {D_{ch}}{N_e}$ | (3) |
1个监测单位的粒子数在监测电离室沉积剂量的绝对值,标记为Dch,abs1 MUU,其中U表示MU的数量,式(3)可表述为Dch,bas=Dch,abs1 MUU。入射电子数量Ne可用式(4)表述:
| ${N_e} = \frac{{D_{ch,abs}^{1MU}}}{{{D_{ch}}}}U$ | (4) |
如取U=1,则加速器输出1 MU相当于${N_e} = \frac{{D_{ch,abs}^{1MU}}}{{{D_{ch}}}}$个入射电子。把式(4)代入式(2),得到水模体中任意体素的绝对剂量,如式(5)所示,该式适用于任何射野大小,可用于开野或者多射野IMRT计划的计算。由公式可知,Dxyz,abs与入射粒子数Ne无关。
| ${D_{xyz}} = {D_{xyz}}\frac{{D_{ch,abs}^{1MU}}}{{{D_{ch}}}}U$ | (5) |
对于IMRT计划,m个角度不同的射野,分别模拟计算各个射野的绝对剂量,IMRT计划总剂量由下式给出:
| ${D_{xyz,abs}} = D_{ch,abs}^{1MU}\sum _{i = 1}^m\frac{{D_{xyz}^i}}{{D_{ch}^i}}其中,i = 1, \cdots ,m$ | (6) |
式(6)可应用于IMRT和多弧的VMAT计划,因为牵涉到多叶光栅(MLC)的模型建立,调强子野的MLC序列读取与文件格式转换等,本研究暂不讨论。
3. 加速器模型校准:Dch(10×10)表示10 cm×10 cm标准射野条件下,单个入射电子在监测电离室的剂量沉积。因此,式(3)改为:Dch,abs1 MU=Dch(10×10)N1 MUe,而式(2)可以改为:Dxyz,abscal=DxyzN1 MUecal,结合式(2)和(3)得到式(7):
| $D_{ch,abs}^{1MU} = {D_{ch\left( {10 \times 10} \right)}}\frac{{D_{xyz,abs}^{cal}}}{{D_{xyz}^{cal}}}U$ | (7) |
需要注意的是,与Dch(10×10)或N1 MUe不同,Dch,abs1 MU为常量,不涉及任何特定的射野尺寸。到此,绝对剂量式(5)可以表述为式(8):
| ${D_{xyz,abs}} = {D_{xyz}}{{{D_{ch\left( {10 \times 10} \right)}}} \over {{D_{ch}}}}{{D_{zyz,abs}^{cal}} \over {D_{xyz}^{cal}}}U$ | (8) |
把式(1)代入式(8)得到式(9):
| ${D_{xyz,abs}} = {D_{xyz}}{{D_{ch}^{forward} + D_{ch\left( {10 \times 10} \right)}^{back}} \over {D_{ch}^{forward} + D_{ch}^{cal}}}{{D_{zyz,abs}^{cal}} \over {D_{xyz}^{cal}}}U$ | (9) |
4.射野输出因子模拟与测量:考虑到射野大小与探测器有效测量体积的相对关系,本研究输出因子的测量采用德国PTW公司半导体探测器(PTW 60016)(1 cm ×1 cm~3 cm×3 cm)和0.125 cc电离室(PTW 31010)(4 cm×4 cm~40 cm×40 cm),测量条件为SSD=100 cm,测量深度为10 cm。PTW 60016为半导体探测器,有效测量体积为0.03 mm3,空间分辨率较高,可用于小尺寸辐射野剂量学数据测量,包括PDD、 profile和输出因子测量。PTW 31010电离室有效测量体积为0.125 cm3,可用于较大射野的剂量学数据测量。蒙特卡罗模拟中,相对射野输出因子(ROF)定义标准水模体中射野中心轴上特点深度处,单个入射电子的剂量沉积相对于标准射野(10 cm ×10 cm)的比值,由式(5)可知ROF的计算公式如下式所示:
| $\begin{array}{l} ROF = \frac{{{D_{xyz,abs}}}}{{{D_{xyz,abs\left( {10 \times 10} \right)}}}} = \frac{{{D_{xyz}}\frac{{D_{ch,abs}^{1MU}}}{{{D_{ch}}}}U}}{{{D_{xyz,abs\left( {10 \times 10} \right)}}\frac{{D_{ch,abs}^{1MU}}}{{{D_{ch\left( {10 \times 10} \right)}}}}U}}\\ = \frac{{{D_{xyz,abs}}}}{{{D_{xyz\left( {10 \times 10} \right)}}}}\frac{{{D_{ch\left( {10 \times 10} \right)}}}}{{{D_{ch}}}} \end{array}$ | (10) |
式中,Dxyz为蒙特卡罗模拟中射野中心轴上的参考深度处(本研究取水下10 cm)的剂量值,Gy/粒子,表示单个电子打靶后在射野中心轴上某深度处的沉积剂量。Dxyz的值可以在DOSXYZnrc程序生成的egslst文件中获取。ROF的相对偏差(Dev.)由式(11)得到:
| $Dev. = {{RO{F_{MC}}RO{F_{Meas.}}} \over {RO{F_{Meas.}}}}$ | (11) |
5.数据处理:本研究采用OriginPro 8.0软件进行数据处理,均值和标准差均由软件给出,相关数据可从模拟结果的egslst文件中直接读取。
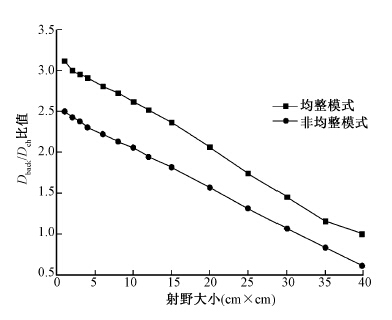
结果1. 相对射野输出因子: 6 MV FF与FFF模式次级准直器反射在监测电离室的剂量沉积Dback占监测电离室总的剂量沉积Dch的百分比与射野的相对关系基本成反比,分别为2.33%±0.71%和1.79%±0.62%,如图 2所示,即次级准直器的反射对监测电离室的影响FF模式相对较大,平均为FFF模式的1.32倍。
|
图 2 均整与非均整模式Dback/Dch比值与射野大小的关系 Figure 2 Relationship between the ratio Dback/Dch and the field size for FF and FFF models |
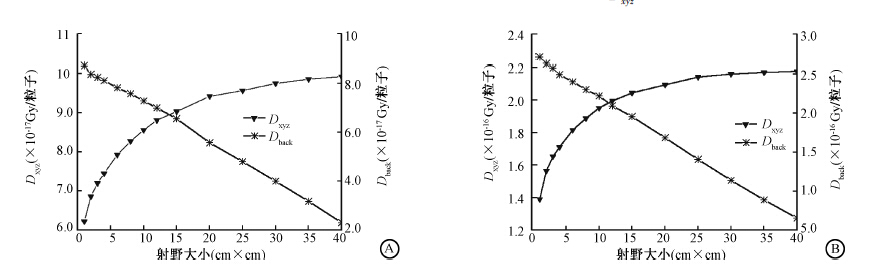
不同射野次级准直器反射在监测电离室的剂量沉积Dback与特定深度处射野中心轴上剂量沉积Dxyz的相对关系如图 3所示。研究表明,Dxyz与射野大小成正比,FFF模式平均为FF模式的2.2倍; Dback大小与射野成反比,FFF模式平均为FF模式的3倍。
|
图 3 均整与非均整模型Dxyz 与Dback值与射野大小的关系 A.均整模式; B.非均整模式 Figure 3 The relationship between Dxyz andDback and field size for FF and FFF models A. FF mode; B. FFF model |
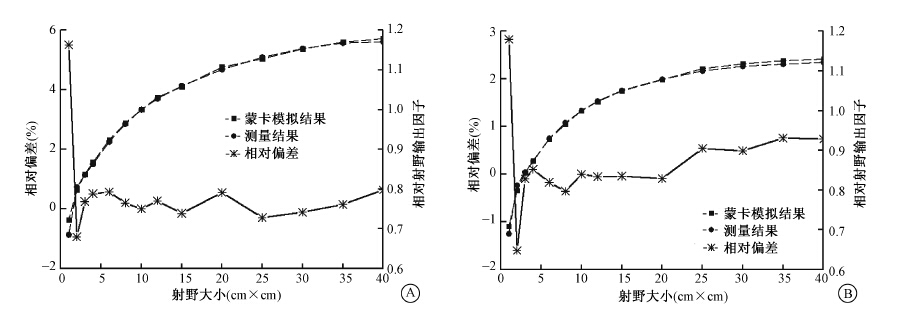
6 MV FF与FFF模型射野相对输出因子的蒙特卡罗模拟与测量值及其相对偏差(Dev.)结果如图 4所示,相对偏差取绝对值后的平均值和标准差分别为0.72%±1.4%、 0.58%±0.78%,两种模式下小于2 cm× 2 cm的小尺寸辐射野的ROF偏差较大。
|
图 4 均整与非均整模式相对射野输出因子和相对偏差 A.均整模式; B.非均整模式 Figure 4 The ROF and Dev. of FF and FFF models A. FF model; B. FFF model |
2. 绝对剂量刻度:对于10 cm×10 cm标准照射野,由模型BEAM_up得到均整与非均整模式下入射电子在监测电离室的剂量沉积Dchforward的值分别为2.706×10-15±1.624×10-17和1.056×10-14±2.112×10-17;由模型BEAM_down得到两种模式下次级准直器反散对在监测电离室内的剂量沉积Dchback的值分别为7.288×10-17±4.373×10-19和2.192×10-16±1.534×10-18。由DOSXYZnrc程序模拟两种模式下入射电子在射野中心轴上参考校准深度处(本研究选取10 cm处)的剂量沉积Dxyzcal分别为8.558×10-17±1.712×10-19和1.952×10-16±1.952×10-19,以上参数的单位均为Gy/粒子。两种模式的Dxyz,abscal分别为0.663和0.634 cGy/MU。把以上参数代入公式(9)得到公式(12):
| $D_{xyz,abs}^{cal} = {D_{xyz}}{{0.215{\rm{ }}3\left( {0.350{\rm{ }}1} \right)} \over {2.706 \times {{10}^{ - 15}}\left( {1.056 \times {{10}^{14}}} \right) + D_{ch}^{back}}}{\rm{ }}U$ | (12) |
公式(11)表示FF与FFF模式下加速器输出1 MU时在监测电离室得到的剂量沉积分别为21.53和35.01 cGy,该值由公式(13)和(14)推导得到:
| $\eqalign{ & \left[ {D_{ch}^{forward} + D_{ch(10 \times 10)}^{back}} \right]{{D_{xyz,abs}^{cal}} \over {D_{xyz}^{cal}}} = \left( {2.706 \times {{10}^{ - 15}} + 7.288 \times {{10}^{ - 17}}} \right) \cr & {{0.663} \over {8.558 \times {{10}^{ - 17}}}} = 21.53cGy \cr} $ | (13) |
| $\eqalign{ & \left[ {D_{ch}^{forward} + D_{ch(10 \times 10)}^{back}} \right]{{D_{xyz,abs}^{cal}} \over {D_{xyz}^{cal}}} = \left( {21.056 \times {{10}^{ - 14}} + 2.192 \times {{10}^{ - 16}}} \right) \cr & {{0.634} \over {1.952 \times {{10}^{ - 16}}}} = 35.01cGy \cr} $ | (14) |
根据公式${N_e} = \frac{{D_{ch,abs}^{1MU}}}{{{D_{ch}}}}U$或$N_e^{1MU} = \frac{{D_{xyz,abs}^{cal}}}{{D_{xyz}^{cal}}}$,本研究的FF和FFF模型标准射野下,1 MU分别相当于7.747×1013±3.099×1011和3.248×1013±1.624×1011个电子打靶,结合射野输出因子,可以得到各个射野的绝对剂量刻度因子,进而完成模型的绝对剂量刻度。
讨论立体定向放射治疗(SBRT)和立体定向放射外科治疗(SRS)在早期小细胞肺癌、 肝癌和颅内多发或单发转移瘤的放射治疗中显示了较明显的优势[7-10],尤其非均整模式下(FFF)的SRS和SBRT技术具有剂量跌落快,正常组织受量低,治疗时间缩短等优点[11-12],对于提高患者生存率和肿瘤局部控制率,降低患者辐射风险具有较大优势。电子打靶产生的原初光子经过均整器后损失较大,并产生较大的散射线[13],因此Dback/Dch的比值,FF模式为FFF模式的1.32倍。均整器的去除致使机头散射明显降低,射线质变软,射野内粒子通量显著提高,剂量率明显增加,可以缩短治疗时间,提高治疗效率[14-15]。
临床上探测器(电离室或宝石探测器)在FFF模式下的绝对剂量刻度工作中,受限于探测器的饱和效应(>500 MU/min),尤其小尺寸辐射野下探测器的体积效应,能量响应等特性,导致剂量刻度偏差与基准数据测量偏差较大[16-17]。现阶段的研究主要集中在利用蒙特卡罗建立直线加速器和探测器模型,通过模拟和计算探测器能量响应、 体积效应、 饱和效应等参数,得到探测器修正因子,进一步确定适合高剂量率和小尺寸辐射野条件下的参考探测器。因此,直线加速器蒙特卡罗模型的建立和绝对剂量刻度工作显得尤为重要。关于3 cm×3 cm以下小尺寸辐射野输出因子的测量,由于探测器的体积效应、 源的遮挡效应和射野内电子不平衡等,使测量结果偏差较大,进一步导致模拟和测量结果偏差较大。英国国家物理研究所(NPL)对于小尺寸辐射野的研究比较深入,近期发表的成果主要有探测器对小尺寸辐射野的影响,探测器的扰动因子和辐射剂量因子等[18-19],研究显示小尺寸高能光子照射野的质量修正因子主要依赖于水和探测器材料电子密度差异以及探器空腔体积的影响,蒙特卡罗模拟对于描述笔形束扰动因子和探究兆伏级光子小尺寸照射野辐射剂量因子特性是非常有帮助的。在临床应用中,当照射野大于探测器扰动区域时辐射剂量因子是无效的。特定的探测器和射线质,充分考虑探测器几何形状对于确定临界射野尺寸是非常必要的。
本研究在现有的均整与非均整模式的蒙特卡罗模型基础上,确定了模型的绝对剂量刻度因子和射野输出因子,为复杂的调强放疗计划方案的蒙特卡罗模拟和对比研究提供了必要的模型基础,同时为探测器模型的剂量刻度研究提供了基本的方法依据。本研究射野输出因子的蒙特卡罗模拟与实测值偏差基本在1%以内,除小于2 cm× 2 cm射野以外,进一步说明了该模型和方法的可靠性和科学性。为了提高模拟精度,降低模拟结果的不确定度度,本研究提高BEAM_up模型入射电子数,分别产生56和48 G相空间文件(EGSnrc设置相空间文件最大为56 G),有效避免了在BEAM_down 模型中由于相空间文件输入源所含光子数目较少带来的非独立事件造成的误差,DOSXYZnrc模拟射野中心轴上特定深度处的剂量沉积采用ISOURCE 9也是基于这样的考虑,由于重复模拟及头部分,增加了模拟的时间成本。
本研究下一步的研究方向是以现有的模型和研究成果为基础,一方面模拟动态调强放射治疗(DIMRT),容积调强放射治疗(VMAT)计划的精确性验证,另一方面针对小尺寸辐射野,特别是<1 cm×1 cm的极小野剂量学研究。
利益冲突 本人与本人家属、 其他研究者,未因进行该研究而接受任何不正当的职务或财务利益,在此对研究的独立性和科学性予以保证作者贡献声明 岳海振负责设计研究方案,收集数据后统计并起草论文;张艺宝负责文章校对;胡俏俏、 刘卓伦、 蒋璠和弓健负责输出因子数据测量和整理;吴昊指导、 监督试验进行和修改论文
| [1] | Lechner W, Kragl G, Georg D. Evaluation of treatment plan quality of IMRT and VMAT with and without flattening filter using Pareto optimal fronts[J]. Radiother Oncol , 2013, 109 (3) : 437-441 DOI:10.1016/j.radonc.2013.09.020 |
| [2] | Navarria P, Ascolese AM, Mancosu P, et al. Volumetric modulated arc therapy with flattening filter free (FFF) beams for stereotactic body radiation therapy (SBRT) in patients with medically inoperable early stage non small cell lung cancer (NSCLC)[J]. Radiother Oncol , 2013, 107 (3) : 414-418 DOI:10.1016/j.radonc.2013.04.016 |
| [3] | Boda-Heggemann J, Mai S, Fleckenstein J, et al. Flattening-filter-free intensity modulated breath-hold image-guided SABR (Stereotactic ABlative Radiotherapy) can be applied in a 15-min treatment slot[J]. Radiother Oncol , 2013, 109 (3) : 505-509 DOI:10.1016/j.radonc.2013.09.014 |
| [4] | Rogers DWO, Walters BR, Kawrakow I. BEAMnrc users manual[J]. Nrc Report Pirs , 2004 : 1-288 |
| [5] | Walters BR, Kawrakow I, Rogers DWO, et al. DOSXYZnrc users manual[J]. Nrc Report Pirs , 2010 : 1-125 |
| [6] | Popescu IA, Shaw CP, Zavgorodni SF, et al. Absolute dose calculations for Monte Carlo simulations of radiotherapy beams[J]. Phys Med Biol , 2005, 50 (14) : 3375-3392 DOI:10.1088/0031-9155/50/14/013 |
| [7] | Nestle U, Guckenberger M. [Stereotactic body radiotherapy for malignant nodules in the lung][J]. Zentralbl Chir , 2013, 138 (Suppl 1) : S25-31 DOI:10.1055/s-0033-1350866 |
| [8] | Mancini BR, Park HS, Harder EM, et al. Elderly patients undergoing SBRT for inoperable early-stage NSCLC achieve similar outcomes to younger patients[J]. Lung Cancer , 2016, 97 : 22-27 DOI:10.1016/j.lungcan.2016.04.011 |
| [9] | Dionisi F, Guarneri A, Dell'Acqua V, et al. Radiotherapy in the multidisciplinary treatment of liver cancer:a survey on behalf of the Italian Association of Radiation Oncology[J]. Radiol Med , 2016, 121 (9) : 735-743 DOI:10.1007/s11547-016-0650-5 |
| [10] | Smith TR, Lall RR, Lall RR, et al. Survival after surgery and stereotactic radiosurgery for patients with multiple intracranial metastases:results of a single-center retrospective study[J]. J Neurosurg , 2014, 121 (4) : 839-845 DOI:10.3171/2014.4.JNS13789 |
| [11] | Stieler F, Fleckenstein J, Simeonova A, et al. Intensity modulated radiosurgery of brain metastases with flattening filter-free beams[J]. Radiother Oncol , 2013, 109 (3) : 448-451 DOI:10.1016/j.radonc.2013.10.017 |
| [12] | Reggiori G, Mancosu P, Castiglioni S, et al. Can volumetric modulated arc therapy with flattening filter free beams play a role in stereotactic body radiotherapy for liver lesions? A volume-based analysis[J]. Med Phys , 2012, 39 (2) : 1112-1118 DOI:10.1118/1.3679858 |
| [13] | Fu W, Dai J, Hu Y, et al. Delivery time comparison for intensity-modulated radiation therapy with/without flattening filter:a planning study[J]. Phys Med Biol , 2004, 49 (8) : 1535-1547 DOI:10.1088/0031-9155/49/8/011 |
| [14] | Vassiliev ON, Titt U, P nisch F, et al. Dosimetric properties of photon beams from a flattening filter free clinical accelerator[J]. Phys Med Biol , 2006, 51 (7) : 1907-1917 DOI:10.1088/0031-9155/51/7/019 |
| [15] | Salter BJ, Sarkar V, Wang B, et al. Rotational IMRT delivery using a digital linear accelerator in very high dose rate 'burst mode'[J]. Phys Med Biol , 2011, 56 (7) : 1931-1946 DOI:10.1088/0031-9155/56/7/002 |
| [16] | Tyler MK, Liu PZ, Lee C, et al. Small field detector correction factors:effects of the flattening filter for Elekta and Varian linear accelerators[J]. J Appl Clin Med Phys , 2016, 17 (3) : 6059 |
| [17] | Ravichandran R, Binukumar JP, Al AI, et al. Diamond detector in absorbed dose measurements in high-energy linear accelerator photon and electron beams[J]. J Appl Clin Med Phys , 2016, 17 (2) : 5690 |
| [18] | Bouchard H, Seuntjens J, Duane S, et al. .Detector dose response in megavoltage small photon beams.I.Theoretical concepts[J]. Med Phys , 2015, 42 (10) : 6033-6047 DOI:10.1118/1.4930053 |
| [19] | Bouchard H, Kamio Y, Palmans H, et al. Detector dose response in megavoltage small photon beams.Ⅱ.Pencil beam perturbation effects[J]. Med Phys , 2015, 42 (10) : 6048-6061 DOI:10.1118/1.4930798 |
 2017, Vol. 37
2017, Vol. 37


