2. 610041 成都, 四川大学华西医院肿瘤放射物理技术中心
2. Radiation Oncology Physics Technical Center, West China Hospital of Sichuan University, Chengdu 610041, China
随着放射治疗技术的发展,调强放疗(IMRT)以及容积旋转调强(VMAT)等技术显著提高了疗效的同时,也使得临床治疗前的剂量验证更加复杂。因临床常规照射与三维适形放疗(3D-CRT)的剂量计算与实现方式相对简单,由相关机器参数引起的误差较小,故使用手工核对的方法即可进行剂量验证[1-3]。而对于调强放疗等技术,传统的手工计算核对和单点剂量的验证已经不再适用[4-5],目前普遍使用的是模体实测的方法,虽然它可以较全面地验证调强的剂量分布,但是这种方法不仅耗费时间和人力[6],而且还需要占用加速器时间,这不仅会影响患者的治疗,还会增加机器的劳损[7]。因此,发展快速有效的剂量验证工具来验证这些复杂的技术很有必要。目前世界上已经有多个放疗中心在尝试实践独立算法软件核对机器跳数(MU)的验证方法[8-10],且可对治疗计划系统(TPS)中复杂的剂量算法提供二次验证。独立的算法验证作为放射治疗质量保证(QA)的一部分已经在很多文章中被提及[1, 5, 11-12],所采用的方法一般分为基于修正和基于模型的两种剂量验证。其中,在3D-CRT技术中两种方法都可以用来验证,而针对调强放疗技术由于其复杂性更适合采用后者进行较为精确的剂量验证。本文根据剂量验证所采用的方法和算法进行分类归纳。
一、 独立剂量验证的必要性放疗的最终目的是尽最大可能提高治疗增益比。目前兴起的IMRT和VMAT等技术在剂量分布上已经很好地契合了这一点,但是由于技术复杂,实施步骤比较繁琐,导致病人在放疗过程中可能会因为某些不确定性因素接受到与处方剂量不相匹配的照射。根据国际辐射单位与测量委员会(ICRU)50号报告[13],靶区剂量偏离处方剂量±5%时,就有可能使原发灶肿瘤失控(局部复发)或放射并发症增加,肿瘤的类别和分期不同,对精确性(5%)的要求也会不同。美国医学物理学家协会工作组(AAPM)40号报告[11]建议在治疗前需要对治疗计划进行独立的机器跳数(MU)检验,并指出两种计算跳数的差异一般情况下应该在2%以内,但是在算法比较复杂时,5%更符合实际情况,该范围一般根据放射治疗采用的技术和算法的复杂程度来设定[14-15]。因此,治疗前进行准确的剂量验证是判断放疗计划能否准确安全实施最重要的指标之一。目前剂量验证的方法一般有模体内剂量实测、跳数的独立核对(手工独立计算和第三方软件计算)和蒙特卡罗模拟。现在被广泛采用的是模体内剂量实测的方法,但是其操作复杂、较为费时而且还需要占用加速器时间[7],给临床工作带来了不便。相比之下,独立的算法验证不仅操作简单而且节约了验证时间,考虑到这些因素,目前的研究认为发展独立的算法验证很有必要[1, 8, 16-17]。
二、 基于修正方法的剂量验证基于修正的剂量计算模式是指以参考条件下实验测量标准野所得的深度剂量、离轴比、散射因子等参数为基础,对其进行必要修正后,得到实际治疗射野内部分点剂量的计算方法。该方法是对参考条件下测量数据的直接或间接调用,这些数据依赖于实验条件和实验模型,被用于实际剂量计算时还需要根据实际情况进行校正,如射野形状、人体轮廓、组织不均匀性、楔形板的使用等。
1.深度剂量-离轴比经验模型:常规放疗都是采用一维或二维表格的形式来表达射野中心轴上和离轴的剂量分布。而从理论上讲,中心轴剂量与离轴剂量的分布相结合就能得到完整的三维射野剂量分布,也就是说肿瘤中任意一点的吸收剂量都可以通过对射野离轴比(OAR)修正来获得[18]。早期的剂量分布计算方法通常表达为百分深度剂量(PDD)和离轴比两个函数的乘积。之后由Khan和Gibbons[19]与欧洲放射肿瘤学会(ESTRO)不断发展[20-21],其函数形式也变得日益复杂,AAPM 114[1]与71[22]号报告里就指出均匀水模体内任意一点P的吸收剂量可用方程式(1)表示。
| $ \begin{array}{*{20}{c}} {D = MU \cdot D{'_0} \cdot {S_{\rm{c}}}\left( {{r_{\rm{c}}}} \right) \cdot {S_{\rm{p}}}\left( {{r_{\rm{d}}}} \right) \cdot {\rm{TPR}}\left( {d,{r_{\rm{d}}}} \right) \cdot \left( {\frac{{{\rm{SS}}{{\rm{D}}_0} \pm {d_0}}}{{{\rm{SPD}}}}} \right) \cdot }\\ {{\rm{OAR}}\left( {d,x} \right) \cdot TF \cdot WF\left( {d,r,x} \right)} \end{array} $ | (1) |
式中,D为所求点的吸收剂量,cGy;D0为参考射野在最大剂量处的校准剂量率,cGy/MU;rc为准直器在等中心平面的射野大小,rd为模体中深度d处的射野大小;Sc(rc)为准直器散射因子;Sp(rd)为模体散射因子;TPR为组织模体比;SSD0为源到模体表面的距离,cm;SPD为源到计算点的距离,cm;d0为标准深度;OAR是离轴比;TF为托架因子;WF为楔形因子。这种经验模型简单易懂, 对诸多条件作了近似处理,比如对总散射因子不作区分或者不考虑介质的非均匀性等。这虽然对模型的计算精度有所影响,但计算速度得以提高且方便了验证软件的使用,适合手工或计算器处理。即使是在TPS迅速发展的今天,有些单位仍然会借助这种模型进行单点的剂量验证,并取得了较好的实验结果,有研究表明,若忽略组织非均匀性的影响,pinnacle计划系统和手工计算的MU其平均差异在1%以内[23]。另外也有研究通过内置这种算法模块的软件(RadCalc、RVP)或者自编译算法软件(MS-Excel)对多种治疗计划进行了单点或多点的剂量验证,证实了软件的准确性和临床可用性,这些软件在使用前,也需要做相关的测试[5, 14-15, 24-25]。在临床允许的剂量误差范围内,独立的MU验证作为一种快速有效的QA工具可以用来帮助识别和减少放疗中的错误[1]。由于算法验证的目的主要在于改善测量验证所带来的时间和人力的耗费。因此,在不明显降低计算精度的条件下,独立的算法验证软件应尽量简单和容易使用[26]。
2. Clarkson积分模型:Clarkson积分模型是二维卷积模型的雏形,开始使用散射的概念进行任意点的剂量计算, 对于不规则野的剂量分布同样适用[27]。该模型由Clarkson提出,基本思想是利用原、散射线模型,以计算点为圆心,将不规则射野等分成36个小扇形分别处理。类似地,对于不规则射野的处理方法还有面积周长比法和Day法。从计算结果的精确度来看,当计算点位于射野中心区域且无遮挡时,面积周长比法较其他两种方法更合适,既未降低准确度,使用起来也不复杂[28],而Day法[29]和Clarkson积分法都是基于将原、散射线分开处理的近似理论,其结果的准确程度基本相同。
对于调强放疗的剂量验证,基于独立子野的Clarkson积分或基于散射的计算方法在临床上也已经得到了应用与发展[10, 30-31]。Kung等[32]和Yang等[8]在此基础上先后对Clarkson方法做了改进,进一步解决了IMRT实施中散射线比较明显以及多叶准直器(MLC)叶片穿透率等问题,其中Kung提出了改进的Clarkson积分(MCI)算法,相比于常规Clarkson积分法,MCI沿着中心轴线的方向,将射野划分成一个个环形区域,并利用散射的旋转对称性来简化剂量的计算,结果显示,5例IMRT计划采用不同算法计算出的中心点剂量的差异都在±3%之间。而Yang等[8]通过改进的Clarkson方法计算散射剂量,解决了机头散射的问题,剂量验证也不再局限于中心轴上的点,而是可以实现任意点的剂量计算与验证。当然对于复杂的调强计划,不仅需要点剂量的验证,还需要平面剂量验证甚至是三维剂量验证才能保证照射剂量的准确性。因此,有报道指出应采用卷积叠加或蒙特卡罗模拟这些更精确的模型对调强放疗计划进行独立的剂量验证[2, 6, 16]。
三、 基于模型方法的剂量验证基于模型的剂量计算方法充分考虑了射线与物质的相互作用,将任意一点的剂量都分成原射线和散射线剂量,并根据各自的特性采用不同的剂量计算模型分别计算。目前常用的基于模型的剂量算法有卷积叠加算法、蒙特卡罗算法等。剂量计算模型的复杂性表现在它对射线与物质相互作用物理过程模拟的逼近程度,模型越趋近于射线吸收的真实物理过程, 表现形式就越复杂,精度也就越高。
1.基于点核和笔形束核的卷积/叠加(convolution/superposition)模型:卷积叠加算法模型来源于Boyer和Mok[33],Mohan等[34]和Mackie等[35]在各自研究中提出的几种类似的剂量计算模型,其原理都是利用点核与原射线穿过人体组织时在单位质量物质中所释放的总能量(TERMA)进行卷积叠加计算。卷积法适用于任意射野的剂量分布计算,在点核相对于空间保持不变的情况下,还可以通过快速傅立叶变换(FFT)来完成对卷积的加速,而对于肺组织而言,相比于蒙特卡罗模拟和常规卷积叠加算法,FFT明显高估了其剂量分布。这是因为在严格意义上,只有单能、平行的射束照射到无限均匀的吸收体时,才能满足核的空间不变性,而实际条件下不同的组织、射线的硬化、射束的发散以及带电粒子的污染等因素都会使点核发生改变[36]。因此,为了得到更精确的剂量分布,采用空间变化核做叠加会更合理,但同时也会增加计算时间。随后,Ahnesj[37]提出了筒串卷积叠加算法(CCCS),进一步缩短了计算时间。因为卷积叠加模型兼顾了临床对计算精度和速度的需求,目前的TPS大多也是采用这种算法。因此,有人建议可以用第二套TPS来实现剂量的验证,Anjum等[38]和Arumugam等[39]就曾用两套TPS互相验证剂量计算的准确性来进行独立的剂量验证。前者是用Eclipse来验证Corvus计算的剂量分布,后者则是Xio和Pinnacle系统的相互验证,研究结果均证实了用第二套TPS独立验证剂量的可行性。AAPM 114[1]报告也对使用第二套TPS作剂量验证时的情况提出了相关建议。
另外,为了有效减少基于笔形束核卷积的计算时间,Bourland和Chaney[40]提出了有限笔束(FSPB)的概念,即假设照射野是由若干个截面为有限大小的笔形束组成,则模体中任意一点的剂量是这些有限笔束在此点产生的剂量叠加。最近,Park等[6]在此基础上进一步发展,在其研究中展示了一种有效的自适应基于细束的有限笔形束(AB-FSPB)剂量计算方法,该方法大大简化了计算程序,而且并未丧失精度,与并行图形处理单元(GPU)相结合,在5 s内就可以计算出调强计划1个子野三维方向的剂量分布。研究还指出若同时考虑精度和计算速度,该算法比其他基于细束的笔形束算法更有优势,这也使其今后能够用于日常的临床IMRT和VMAT计划独立剂量验证成为可能。
2.蒙特卡罗(MC)模型:蒙特卡罗方法是一种基于“随机数”的计算方法。该模型针对待求问题,根据物理现象本身的统计规律,进行大统计量的统计实验或计算机随机模拟,一次计算至少需要模拟百万数量级的粒子才能满足统计误差的要求,也正因为其利用大统计量处理复杂问题(复杂的几何、复杂的放射源布置等)的能力而具有不可替代性。蒙特卡罗模型用于剂量计算的原理在于,用统计学的方法模拟大量光子在输运过程中与物质的相互作用。由于能在使用较少近似的情况下对放射物理过程进行精确地建模,蒙特卡罗模拟方法被认为是最精确的剂量计算方法[41]。近年来,Ma等[42]、Pawlicki和Ma[43]、Davidson等[44]和Dogan等[45]已经实现了将MC方法用于调强计划的独立剂量验证。但是将其用于日常的临床验证仍然受到计算耗时较长的限制[46]。而随着计算机运算速度的迅速提高和GPU的快速发展,这一问题正在逐步得到解决。目前应用比较广泛的蒙特卡罗模拟软件有EGSnrc(BEAMnrc和DOSEnrc),Lourens[47]和Ishihara等[48]都用此软件做过剂量验证的研究,并证实了蒙特卡罗方法具有很高的准确性,其中,Lourens[47]认为现代具有并行处理器的计算机可以实现MC的快速计算,对于较复杂的IMRT计划的剂量计算也可以在合理的时间内完成。针对耗时长的缺点,也有很多快速蒙特卡罗模拟软件(VMC/XVMC、MCDOSE等)被开发出来以满足临床使用,与普通软件的计算方法比较,这类软件引入了各种方差缩减技巧来缩短计算时间[41]。另外,现在比较新的MC验证方法采用的都是患者的CT扫描数据,与一般基于水模体的实测验证方法相比,其模拟结果也更接近于患者体内真实的剂量分布[49],而由于采用近似算法而引起的剂量计算的不准确性,也更容易被检测出来[41],这在一定程度上也提高了MC方法验证的可信度。最近,Chen等[2]用基于体素的蒙特卡罗系统(VMC)与云计算技术相结合有效地计算出了调强计划的剂量分布,并认为这种方法能适用于临床计划的剂量验证,不仅是VMAT,对于IMRT和3D-CRT也同样适用。蒙特卡罗模拟验证作为一种理论方法,既有模拟精确的优点,又有耗时长的缺点,不过随着计算机技术的快速发展,蒙特卡罗算法也越来越受到关注,并逐渐成为研究的热点,今后也将得到更广泛的使用。
四、 独立的算法验证在临床放疗QA中的应用自从调强技术在临床上被广泛应用以来,为了保证调强放射治疗射野输出剂量的准确性, 必须进行精心的剂量学验证。尽管可以采用很多方法来实现基于剂量的患者个体化(patient-specific)QA,但个体治疗计划的验证方法必需简单高效,因为QA的工作量是随着患者数量的增加而增加的。而医院能否提供准确高效的剂量验证设备与验证方法直接影响着放疗中心治疗患者的效率。同时对英国近两年来IMRT病例的数据分析,显示基于算法的验证方法的增加与放疗中心利用调强技术治疗的患者数相互影响[50]。患者个体化QA仅用于检查严重错误,例如绝对剂量超过了处方剂量的5%等。也有研究建议患者治疗计划完成后,应进行3个步骤的检查,首先设计计划的物理师需要直观判断剂量分布是否正确,然后采用独立的计算机程序验算每个射野的MU,对于简单布野条件,验算值与计划系统的结果差别应控制在2%~3%的范围内,而在复杂布野条件时,差异超过5%的情况应分析原因,最后由高年资的物理师核对全部计划资料[51]。
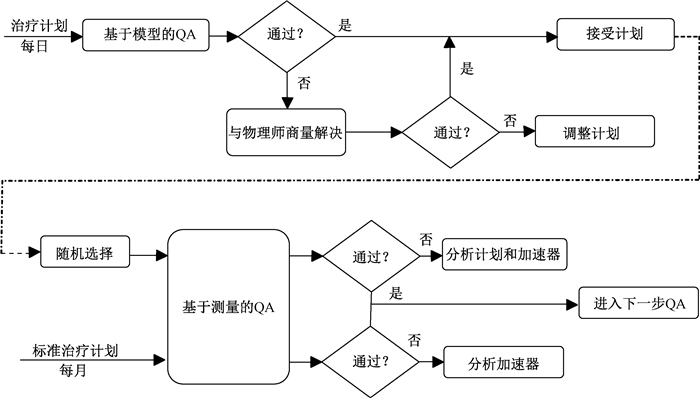
由于点剂量以及某些情况下平面剂量分布的分析与验证不需要加速器的参与,基于软件和算法的验证方法有明显的增长[50]。早期基于简单算法的验证方法并未考虑机头散射的影响,而且剂量的验证也仅限于中心轴上的点[8],因此仅适合于二维与三维适形放疗技术。而IMRT和VMAT照射的通量或者剂量具有较大的梯度,且射野大小和入射角度在照射过程中也是变化的,因此,中心轴上点剂量的验证已不再适用。有研究建议利用独立剂量验证的蒙特卡罗模拟方法先对IMRT计划做初步筛选,而基于测量的验证作为第二道程序只在必要的时候进行[41]。Visser等[52]针对目前IMRT患者不断增加的问题提出了一种快速有效的QA流程即混合式QA,其基本流程图如图 1(译自参考文献[52]中图 1)所示。
|
图 1 混合式QA流程图[52] 注:QA.质量保证 Figure 1 Overview of the hybrid-QA method |
具体流程如下:先将所有的治疗计划用基于模型的独立算法验证,不满足要求的返回与物理师进行商议并调整计划,直到满足临床要求为止;另外对所有满足初筛要求的计划还要进行抽测(约15%的计划),采用测量验证的方法进行第2次验证,若误差在允许范围内,则可以进入下一阶段的临床治疗,反之则对计划和加速器进行分析,找出问题所在。而对于整个系统稳定性的测试,采用每月对某一例经典的标准计划进行重复测量验证的方法来实现。
这种方法综合了基于模型QA的时间有效性和基于测量QA的结果可靠性,可以验证大量复杂的治疗计划,而且缩短了放疗计划的测量QA时间。研究还指出这种混合式QA具有一般性,它可以根据各个放疗中心的实际情况由不同的QA方式混合组成。比如基于模型的蒙卡算法和基于测量的电子射野影像系统(EPID),这也是患者个体化QA的发展方向[53]。
目前并没有某种单一的QA技术能够全面检测并修正放疗计划执行过程中所有可能产生的错误。Pawlicki等[54]早在2008年就曾采用统计学的控制图表方法,对测量验证与算法验证IMRT计划的QA结果进行了分析,结果显示两种方法都还有提升的空间,可以互补互足,不能完全相互取代。Siochi等[55]也针对基于计算的患者个体化QA能否取代基于测量的验证作过讨论。另外,相关研究也应该对传统的QA方法评估其效率和有效性,并结合已有的经验,探索出更有效、系统、可行的方法来拓宽或者替换现有的QA技术。最近就有研究将独立的算法验证与加速器的logfile文件分析相结合共同评估IMRT剂量分布,这样不仅能验证TPS剂量计算的误差,同时也能检测计划数据传输的准确性和加速器MLC的到位精度,而且验证所需的时间相比测量也大为减少[7]。Handsfield等[56]针对螺旋断层放射治疗系统(Tomo)也提出了一种新的双重验证的QA方法即MCLogQA。该方法也是将二次的剂量计算与基于logfile文件分析MLC位移的QA相结合,优势在于能够提供综合的三维剂量验证、采用的是患者原始的CT数据、考虑了组织不均匀性、同时也缩短了计划验证时间,更重要的是对治疗中的每个分次都提供了完整的QA方法。而对立体定向放射外科(SRS)的主要治疗手段伽玛刀来说,由于是单次大剂量的聚焦照射,其剂量验证显得尤为重要。通过各种算法对伽马刀计划(LGP)的剂量验证在相关文献上已有报道[57-59]。Hur等[60]也在此基础上提出了采用改进的可变椭球模型(MVEMT)对LGP作二次验证,并认为MVEMT可以作为参考验证方法,对以后新的验证方法的使用和设计具有参考意义。总之,用于放射治疗独立剂量验证的剂量算法,应该是综合考虑了算法的计算精度、运行速度以及适用技术等多种因素之后最适宜的模型。
五、 总结与展望基于修正方法的剂量验证计算方法较简单,适用于射野注量分布比较均匀的常规照射、3D-CRT以及静态IMRT等技术。而对于动态IMRT和VMAT等复杂技术,由于其射野注量分布不均,剂量梯度较大,单点或者多点的剂量验证不足以判断照射剂量的准确性[61],需要基于模型的更复杂的算法实现剂量验证。蒙特卡罗算法几乎可以覆盖所有放疗技术的剂量验证,精度也满足临床要求,但也会受到较长计算时间的影响。因此,对不同种类的治疗计划进行剂量验证时,应当根据各种算法软件的计算时间和精确程度以及软件本身的性价比来选择合适的剂量验证工具。
从理论上来讲,独立算法验证软件应具备3个特点:准确性(计算结果可靠)、一般性(能够适用于不同的治疗技术)、简单性(不耗费大量时间且容易使用)。算法验证的主要目的是提供一种简单直接且具有一定准确度的剂量验证方法,使剂量差异>5%的计划能够快速地被检查出来,进而对其采用其他更精确的方法做进一步的分析,防止任何的漏照射或过照射[9, 26, 54]。另外需要引起注意的是,算法验证的方法仅仅只是针对TPS的优化算法进行了简单的验证,而对于加速器质量控制特别是MLC的到位精度验证必需同时进行,只有两类验证的结合才能构成严格且完整的QA程序[41, 62]。同时也有研究认为,独立的剂量计算验证方法与周期性MLC的QA相结合才足够完成调强放疗计划的患者个体化QA [6]。实际上,关于调强放疗的剂量验证问题,已经有很多人在其文章和著作中讨论过,但对于“如果实际照射剂量和计划剂量不一致时该如何处理”的问题,却少有人涉及。本文虽然提出了部分解决办法,但这方面还需要进行更多的研究。总之,独立的算法验证具有速度快、精度高、简单易行等特点,在临床治疗与验证方面显示出极大的优势,值得深入研究,并有望与其他QA技术相结合替代传统的基于测量的验证方法[6, 55],完成从补充验证工具到主流剂量验证工具的转变。
利益冲突 本人与本人家属、其他研究者无可能影响研究结果的财务关系,在此对研究的独立性和科学性予以保证作者贡献声明 昌胜负责构思、收集文献和论文撰写;李光俊负责拟定写作思路,指导论文的撰写和修改;柏森负责指导论文的撰写和修改
| [1] | Stern RL, Heaton R, Fraser MW, et al. Verification of monitor unit calculations for non-IMRT clinical radiotherapy:report of AAPM Task Group 114[J]. Med Phys , 2011, 38 (1) : 504-530 DOI:10.1118/1.3521473 |
| [2] | Chen X, Bush K, Ding A, et al. Independent calculation of monitor units for VMAT and SPORT[J]. Med Phys , 2015, 42 (2) : 918-924 DOI:10.1118/1.4906185 |
| [3] | International Atomic Energy Agency. Commissioning and quality assurance of computerized planning systems for radiation treatment of cancer. IAEA TRS 430[R]. Vienna:IAEA, 2004. |
| [4] | Georg D, Stock M, Kroupa B, et al. Patient-specific IMRT verification using independent fluence-based dose calculation software:experimental benchmarking and initial clinical experience[J]. Phys Med Biol , 2007, 52 (16) : 4981-4992 DOI:10.1088/0031-9155/52/16/018 |
| [5] | Sellakumar P, Arun C, Sanjay SS, et al. Comparison of monitor units calculated by radiotherapy treatment planning system and an independent monitor unit verification software[J]. Phys Med , 2011, 27 (1) : 21-29 DOI:10.1016/j.ejmp.2010.01.006 |
| [6] | Park JC, Li JG, Arhjoul L, et al. Adaptive beamlet-based finite-size pencil beam dose calculation for independent verification of IMRT and VMAT[J]. Med Phys , 2015, 42 (4) : 1836-1850 DOI:10.1118/1.4914858 |
| [7] | Sun B, Rangaraj D, Boddu S, et al. Evaluation of the efficiency and effectiveness of independent dose calculation followed by machine log file analysis against conventional measurement based IMRT QA[J]. J Appl Clin Med Phys , 2012, 13 (5) : 673-678 DOI:10.1120/jacmp.v13i5.3837 |
| [8] | Yang Y, Xing L, Li JG, et al. Independent dosimetric calculation with inclusion of head scatter and MLC transmission for IMRT[J]. Med Phys , 2003, 30 (11) : 2937-2947 DOI:10.1118/1.1617391 |
| [9] | Howlett SJ. Enhanced dynamic wedge and independent monitor unit verification[J]. Australas Phys Engineer Sci Med , 2005, 28 (1) : 26-36 DOI:10.1007/BF03178861 |
| [10] | Xing L, Chen Y, Luxton G, et al. Monitor unit calculation for an intensity modulated photon field by a simple scatter-summation algorithm[J]. Phys Med Biol , 2000, 45 (3) : N1-N7 DOI:10.1088/0031-9155/45/3/401 |
| [11] | Kutcher GJ, Coia L, Gillin M, et al. Comprehensive QA for radiation oncology:report of AAPM Radiation Therapy Committee Task Group 40[J]. Med Phys , 1994, 21 (4) : 581-618 DOI:10.1118/1.597316 |
| [12] | Fraass B, Doppke K, Hunt M, et al. American Association of Physicists in Medicine Radiation Therapy Committee Task Group 53:quality assurance for clinical radiotherapy treatment planning[J]. Med Phys , 1998, 25 (10) : 1773-1829 DOI:10.1118/1.598373 |
| [13] | Jones D. ICRU Report 50:prescribing, recording and reporting photon beam therapy[J]. Med Phys , 1994, 21 (6) : 833-834 DOI:10.1118/1.597396 |
| [14] | Curtis H, Richmond N, Burke K, et al. Determination of monitor unit check tolerances based on a comparison with measurement and treatment planning system data[J]. Med Dosim , 2013, 38 (1) : 81-87 DOI:10.1016/j.meddos.2012.07.005 |
| [15] | Nordström F, Af Wetterstedt S, Johnsson S, et al. Control chart analysis of data from a multicenter monitor unit verification study[J]. Radiother Oncol , 2012, 102 (3) : 364-370 DOI:10.1016/j.radonc.2011.11.016 |
| [16] | Pisaturo O, Moeckli R, Mirimanoff RO, et al. A Monte Carlo-based procedure for independent monitor unit calculation in IMRT treatment plans[J]. Phys Med Biol , 2009, 54 (13) : 4299-4310 DOI:10.1088/0031-9155/54/13/022 |
| [17] | Low DA, Moran JM, Dempsey JF, et al. Dosimetry tools and techniques for IMRT[J]. Med Phys , 2011, 38 (3) : 1313-1338 DOI:10.1118/1.3514120 |
| [18] | Chui CS, Mohan R. Off-center ratios for three-dimensional dose calculations[J]. Med Phys , 1986, 13 (3) : 409-412 DOI:10.1118/1.595886 |
| [19] | Khan FM, Gibbons JP. Khan's the physics of radiation therapy[M]. Baltimore: Lippincott Williams & Wilki, 2014 . |
| [20] | Dutreix A, Bjärngard BE, Bridier A, et al. Monitor unit calculation for high energy photon beams[M]. Leuven: Garant Publ, ESTRO, 1997 . |
| [21] | Mijnheer B, Bridier A, Garibaldi C, et al. Monitor unit calculation for high energy photon beams:practical examples[M]. Brussels: ESTRO, 2001 . |
| [22] | Gibbons JP, Antolak JA, Followill DS, et al. Monitor unit calculations for external photon and electron beams:report of the AAPM Therapy Physics Committee Task Group No. 71[J]. Med Phys , 2014, 41 (3) : 31501 DOI:10.1118/1.1429629 |
| [23] | Chan J, Russell D, Peters VG, et al. Comparison of monitor unit calculations performed with a 3D computerized planning system and independent "hand" calculations:results of three years clinical experience[J]. J Appl Clin Med Phys , 2002, 3 (4) : 293-301 DOI:10.1120/1.1506379 |
| [24] | Kay I, Dunscombe P. Verifying monitor unit calculations for tangential breast fields[J]. J Appl Clin Med Phys , 2006, 7 (2) : 50-57 DOI:10.1120/jacmp.v7i2.2177 |
| [25] | Leszczynski KW. Independent corroboration of monitor unit calculations performed by a 3D computerized planning system[J]. J Appl Clin Med Phys , 2000, 1 (4) : 120-125 DOI:10.1120/1.1314820 |
| [26] | Linthout N, Verellen D, Van AS, et al. A simple theoretical verification of monitor unit calculation for intensity modulated beams using dynamic mini-multileaf collimation[J]. Radiother Oncol , 2004, 71 (2) : 235-241 DOI:10.1016/j.radonc.2004.02.014 |
| [27] | Clarkson JR. A note on depth doses in fields of irregular shape[J]. Br J Radiol , 1941, 14 (164) : 265-268 DOI:10.1259/0007-1285-14-164-265 |
| [28] | 胡逸民. 肿瘤放射物理学[M]. 北京: 原子能出版社, 2003 . Hu YM. Radiation oncology physics[M]. Beijing: Atomic Energy Press, 2003 . |
| [29] | Day MJ. The equivalent field method for dose determination in rectangular fields[J]. Br J Radiol , 1983, 17 : 105-114 |
| [30] | Zhe C, Lei X, Nath R. Independent monitor unit calculation for intensity modulated radiotherapy using the MIMiC multileaf collimator[J]. Med Phys , 2002, 29 (9) : 2041-2051 DOI:10.1118/1.1500397 |
| [31] | Zhu J, Yin FF, Kim JH. Point dose verification for intensity modulated radiosurgery using Clarkson's method[J]. Med Phys , 2003, 30 (8) : 2218-2221 DOI:10.1118/1.1589495 |
| [32] | Kung JH, Chen GT, Kuchnir FK. A monitor unit verification calculation in intensity modulated radiotherapy as a dosimetry quality assurance[J]. Med Phys , 2000, 27 (10) : 2226-2230 DOI:10.1118/1.1286553 |
| [33] | Boyer A, Mok E. A photon dose distribution model employing convolution calculations[J]. Med phys , 1985, 12 (2) : 169-177 DOI:10.1118/1.595772 |
| [34] | Mohan R, Chui C, Lidofsky L. Differential pencil beam dose computation model for photons[J]. Med Phys , 1986, 13 (1) : 64-73 DOI:10.1118/1.595924 |
| [35] | Mackie TR, Scrimger JW, Battista JJ. A convolution method of calculating dose for 15 MV X rays[J]. Med Phys , 1985, 12 (2) : 188-196 DOI:10.1118/1.595774 |
| [36] | Miften M, Wiesmeyer M, Monthofer S, et al. Implementation of FFT convolution and multigrid superposition models in the focus RTP system[J]. Phys Med Biol , 2000, 45 (4) : 817-833 DOI:10.1088/0031-9155/45/4/301 |
| [37] | Ahnesjö A. Collapsed cone convolution of radiant energy for photon dose calculation in heterogeneous media[J]. Med Phys , 1989, 16 (4) : 577-592 DOI:10.1118/1.596360 |
| [38] | Anjum MN, Parker W, Ruo R, et al. IMRT quality assurance using a second treatment planning system[J]. Med Dosim , 2010, 35 (4) : 274-279 DOI:10.1016/j.meddos.2009.09.001 |
| [39] | Arumugam S, Xing A, Goozee G, et al. Independent calculation-based verification of IMRT plans using a 3D dose-calculation engine[J]. Med Dosim , 2013, 38 (4) : 376-384 DOI:10.1016/j.meddos.2013.04.005 |
| [40] | Bourland JD, Chaney EL. A finite size pencil beam model for photon dose calculations in three dimensions[J]. Med Phys , 1992, 19 (6) : 1401-1412 DOI:10.1118/1.596772 |
| [41] | Goetzfried T, Rickhey M, Treutwein M, et al. Monte Carlo simulations to replace film dosimetry in IMRT verification[J]. Z Med Phys , 2011, 21 (1) : 19-25 DOI:10.1016/j.zemedi.2010.05.002 |
| [42] | Ma CM, Pawlicki T, Jiang SB, et al. Monte Carlo verification of IMRT dose distributions from a commercial treatment planning optimization system[J]. Phys Med Biol , 2000, 45 (9) : 2483-2495 DOI:10.1088/0031-9155/45/9/303 |
| [43] | Pawlicki T, Ma CM. Monte Carlo simulation for MLC-based intensity-modulated radiotherapy[J]. Med Dosim , 2001, 26 (2) : 157-168 DOI:10.1016/S0958-3947(01)00061-9 |
| [44] | Davidson S, Cui J, Followill D, et al. A flexible Monte Carlo tool for patient or phantom specific calculations:comparison with preliminary validation measurements[J]. J Phys Conf Ser , 2008, 102 (1) : 12004 DOI:10.1088/1742-6596/102/1/012004 |
| [45] | Dogan N, Mihaylov I, Wu Y, et al. Monte Carlo dose verification of prostate patients treated with simultaneous integrated boost intensity modulated radiation therapy[J]. Radiat Oncol , 2009, 4 : 18 DOI:10.1186/1748-717X-4-18 |
| [46] | Palta JR, Mackie TR, Chen Z. Intensity-modulated radiation therapy-the state of the art[J]. Med Phys , 2003, 30 (12) : 3265 DOI:10.1118/1.1628279 |
| [47] | Lourens JS. Verification of a commercial treatment planning system based on Monte Carlo radiation dose calculations in intensity modulated radiation therapy[D]. Bloemfontein:University of the Free State (UFS), 2015. |
| [48] | Ishihara Y, Sawada A, Nakamura M, et al. Development of a dose verification system for vero 4DRT using Monte Carlo method[J]. J Appl Clin Med Phys , 2014, 15 (6) : 4961 DOI:10.1120/jacmp.v15i6.4961 |
| [49] | Zarza-Moreno M, Cardoso I, Teixeira N, et al. The use of non-standard CT conversion ramps for Monte Carlo verification of 6 MV prostate IMRT plans[J]. Phys Med , 2013, 29 (4) : 357-367 DOI:10.1016/j.ejmp.2012.05.004 |
| [50] | Abolaban F, Zaman S, Cashmore J, et al. Changes in patterns of intensity-modulated radiotherapy verification and quality assurance in the UK[J]. Clin Oncol , 2016 : 1-7 DOI:10.1016/j.clon.2016.01.013 |
| [51] | 于金明, 于甬华. 放射治疗的质量保证与质量控制[J]. 中国肿瘤 , 2004, 13 (8) : 3-7 Yu JM, Yu YH. Quality assurance and quality control in radiotherapy[J]. China Cancer , 2004, 13 (8) : 3-7 DOI:10.3969/j.issn.1004-0242.2004.08.001 |
| [52] | Visser R, Wauben DJL, Groot MD, et al. Efficient and reliable 3D dose quality assurance for IMRT by combining independent dose calculations with measurements[J]. Med Phys , 2013, 40 (2) : 157 DOI:10.1118/1.4774048 |
| [53] | Elmpt WV, Nijsten S, Mijnheer B, et al. The next step in patient specific QA:3D dose verification for conformal and intensity modulated RT based on EPID dosimetry and monte carlo calculations[J]. Radiot Oncol , 2008, 86 (1) : 86-92 DOI:10.1016/j.radonc.2007.11.007 |
| [54] | Pawlicki T, Yoo S, Court LE, et al. Moving from IMRT QA measurements toward independent computer calculations using control charts[J]. Radiot Oncol , 2008, 89 (3) : 330-337 DOI:10.1016/j.radonc.2008.07.002 |
| [55] | Siochi RA, Molineu A, Orton CG. Point/counterpoint. Patient-specific QA for IMRT should be performed using software rather than hardware methods[J]. Med Phys , 2013, 40 (7) : 70601 DOI:10.1118/1.4794929 |
| [56] | Handsfield LL, Jones R, Wilson DD, et al. Phantomless patient-specific Tomotherapy QA via delivery performance monitoring and a secondary Monte Carlo dose calculation[J]. Med Phys , 2014, 41 (10) : 101703 DOI:10.1118/1.4894721 |
| [57] | Hur BI, Choi BK, Sung SK, et al. The variable ellipsoid modeling technique as a verification method for the treatment planning system of γ knife radiosurgery[J]. J Korean Neurosurg Soc , 2010, 47 (2) : 128-133 DOI:10.3340/jkns.2010.47.2.128 |
| [58] | Tsai JS, Engler MJ, Rivard MJ, et al. A formalism for independent checking of γ knife dose calculations[J]. Med Phys , 2001, 28 (9) : 1842-1849 DOI:10.1118/1.1398038 |
| [59] | Marcu SM, Wu QJ, Pillai K, et al. γ plan-leksell γ knife radiosurgery treatment planning verification method[J]. Med Phys , 2000, 27 (9) : 2146-2149 DOI:10.1118/1.1287051 |
| [60] | Hur BI, Lee JM, Cho WH, et al. Clinical application of gamma knife dose verification method in multiple brain tumors:modified variable ellipsoid modeling technique[J]. J Korean Neurosurg Soc , 2013, 53 (2) : 102-107 DOI:10.3340/jkns.2013.53.2.102 |
| [61] | Xing L, Lin ZX, Donaldson SS, et al. Dosimetric effects of patient displacement and collimator and gantry angle misalignment on intensity modulated radiation therapy[J]. Radiot Oncol , 2000, 56 (1) : 97-108 DOI:10.1016/S0167-8140(00)00192-4 |
| [62] | Xing L, Li JG. Computer verification of fluence map for intensity modulated radiation therapy[J]. Med Phys , 2000, 27 (27) : 2084-2092 DOI:10.1118/1.1289374 |
 2016, Vol. 36
2016, Vol. 36


