中华放射医学与防护杂志  2015, Vol. 35 Issue (9): 670-673   PDF    
引用本文
陈利, 黄晓延, 曹午飞, 姚杏红, 陈阿龙. 肺癌调强计划在水与介质中蒙特卡罗计算的剂量差异[J]. 中华放射医学与防护杂志, 2015, 35(9): 670-673, DOI: 10.3760/cma.j.issn.0254-5098.2015.09.007.
肺癌调强计划在水与介质中蒙特卡罗计算的剂量差异
陈利, 黄晓延 , 曹午飞, 姚杏红, 陈阿龙    
510060 广州, 中山大学肿瘤防治中心放疗科 华南肿瘤学国家重点实验室 肿瘤医学协同创新中心
收稿日期: 2015-01-28
通信作者:黄晓延,Email:huangxiaoy@sysucc.org.cn
[摘要]    目的 探讨肺癌调强放疗计划时,蒙特卡罗算法计算对水与介质的剂量差异。方法随机类型抽样法选取10例肺癌患者的5野调强计划,在质量保证模块下以患者自身图像为模体,采用蒙特卡罗算法分别计算两种计划的吸收剂量,计算对实际介质的吸收剂量(Dm)和对水的吸收剂量(Dw);通过剂量体积直方图的剂量体积参数和计划分析,比较两种剂量在患者体内的分布差异。结果 靶区PTV65和PTV50的D50%、D98%和D2%的Dm和Dw差异分别为:-0.3%、-0.2%、0.3%和0.1%、-0.6%、0.4%,其中PTV65的D50%和PTV50的D98%差异有统计学意义(t=-2.536、-3.776,P<0.05)。正常组织的D50%中,脊髓、心脏、肺和食管的Dm与Dw的平均偏差为0.3%、1.1%、-0.2%和-0.1%,脊髓和心脏的Dm比Dw稍低(t=2.535、3.254,P<0.05);正常组织的D2%的平均偏差为0.3%、-0.6%、-0.7%和0.6%,差异有统计学意义(t=2.311、-4.105、-3.878、6.214,P<0.05)。所有剂量的体积偏差均<2%。对于没有勾画出来的一些骨组织区域,Dm和Dw的偏差>5%。结论 在临床使用过程中,在考虑骨性组织的受照剂量限制时,需要注意肺癌患者的Dm与Dw的相对偏差。
[关键词]     肺癌    调强放疗    蒙特卡罗算法    对介质的剂量    对水的剂量    
The differences between Monte Carlo calculated dose-to-medium and dose-to-water for lung cancer IMRT
Chen Li, Huang Xiaoyan , Cao Wufei, Yao Xinghong, Chen Along    
Department of Radiation Onclology, Sun Yat-sen Universiry Cancer Center;State Key Laboratory of Oncology in South China;Collaborative Innovation Center for Cancer Medicine, Guangzhou 510060, China
[Abstract]    Objective To investigate the differences between Monte Carlo (MC) calculated dose-to-water (Dw) and dose-to-medium (Dm) for lung cancers treated with intensity-modulated radiotherapy (IMRT). Methods A total of 10 lung carcinoma patients with 5-field IMRT treatment plans were stratified sampling randomly selected for this study, which were performed on Monaco treatment planning system (TPS) with MC algorithm. Using the patients' own CT images as quality assurance (QA) phantoms, two kinds of QA plan were calculated, one was the Dm, and another was the Dw plan. Dose volume histogram (DVH) parameters and the subtraction of two plans were used to evaluate the spatial distribution of the difference between the Dm and Dw. Results Differences between dose-volume indices computed with Dm and Dw for the PTV65 and PTV50 doses (D50%, D98% and D2%) were -0.3%,-0.2%,0.3% and 0.1%,-0.6%,0.4%, respectively, of which the D50% of PTV65 and D98% of PTV50 had statistical difference (t=-2.536, -3.776, P<0.05). For normal tissues, spinal cord, heart, lung and esophagus, the D50% differences between Dm and Dw were 0.3%, 1.1%, -0.2% and -0.1%, of which the Dm of spinal cord and heart were slightly lower than the Dw (t=2.535, 3.254, P<0.05). For the D2% of the normal tissues, the differences were 0.3%, -0.6%, -0.7% and 0.6%, the differences were statistically significant (t=2.311, -4.105, -3.878, 6.214, P<0.05). All the differences were within 2%. Meanwhile planned subtraction analysis showed the differences between the Dm and Dw varied very much with the other body parts of the patient, especially for bone tissues, and the two doses were significant difference (>5%). Conclusion In the course of clinical application, the relative differences between Dm and Dw for lung cancers MC calculations should be noted when considering the dose limitations of bone tissue.
[Key words]     Lung cancer    Intensity-modulated radiotherapy    Monte Carlo algorithm    Dose-to-medium    Dose-to-water    

吸收剂量是放射治疗中最基本的物理量。蒙特卡罗算法(Monte Carlo,MC)是公认的准确计算放射治疗剂量的算法,特别是计算密度非均匀组织的吸收剂量,且相比传统的剂量算法,其剂量计算更准确[1, 2]。MC算法已经被投入到商业治疗计划系统(TPS)的使用中[3, 4, 5],而基于MC算法的TPS,使用对介质的吸收剂量(dose-to-medium,Dm)还是对水的吸收剂量(dose-to-water,Dw)存在一定的争议[6]。Bragg-Gray空腔理论计算显示,对高密度的骨组织,MC算法计算的Dm和Dw之间的差异可达10%以上[7],目前使用MC算法的TPS中并无相关报道。本研究基于 V3.20 Monaco TPS的MC算法分别计算了Dm计划和Dw计划,分析总结了患者体内两种剂量的差异,为肺癌的临床计划设计、评价及验证提供一定的参考。

资料与方法

1.病例资料:回顾性地随机类型抽样法选取2014年5月—8月在本科接受放射治疗的肺癌患者10例,其中左肺癌患者5例,右肺癌患者5例。男性9例,女性1例,年龄57~74岁,中位年龄66岁。按美国癌症联合会(AJCC)第7版分期标准[8],Ⅱ期2例,Ⅲ期8例。

2. 计划设计:根据国际辐射单位和测量委员会(ICRU) 50和62号报告[9, 10],在CT图像上勾画所有患者的肿瘤靶区体积(GTV)、亚临床病灶与高危淋巴引流区域临床靶区体积(CTV),及相应外扩得到计划靶区体积(PTV),处方剂量为60和50 Gy的2个计划靶区分别定义为PTV65和PTV50。使用瑞典Elekta公司生产的V3.20 型Monaco计划系统进行计算。选用瑞典Elekta公司生产的Synergy型6 MV X射线,多叶光栅40对,叶片在等中心处投影宽度为1 cm,最大剂量率600 MU/min。对每例患者设计5野静态调强放疗(sIMRT)计划,射束角度随肿瘤的位置变化。使用ICRU 83号报告推荐的"一定体积的"剂量来描述各个结构的剂量信息[11],D2%为近似最大剂量,D98%为近似最小剂量,D50%为中位剂量。各靶区与危及器官的计划剂量约束条件如下:各PTV的V100% ≥95％且V110%≤10％(Vx%[JP+1]为接受x%处方剂量的体积百分比);脊髓近似最大剂量D2%(Dx%为x%的体积接受的照射剂量) < 45 Gy;[JP]肺V20Gy < 35%,平均剂量＜19 Gy;心脏V30Gy < 40%;食管最大剂量＜65 Gy。

3. Dw和Dm的剂量计算:为了计算相同的辐射条件和辐射介质下Dw和Dm的差异,使用质量保证(QA)计划。以患者自身CT影像为QA模体,分别计算两种QA计划,Dm计划是计算对介质的剂量,Dw计划是对水的剂量。MC剂量计算的网格大小为0.3 cm × 0.3 cm × 0.3 cm,每个控制点的标准偏差为3.0%。

4. 靶区及正常组织的剂量计算:通过剂量体积直方图(DVH)统计分析比较两种计算的靶区及正常组织的剂量结果。对每例患者,其靶区及正常组织的Dw和Dm的偏差率(%)计算为Diff(%)=[(Dx%)w - (Dx%)m]/(Dx%)w × 100%,同时计算10个病例的平均偏差结果。考虑到DVH给出的结果只是基于统计的结果,而没有空间位置的剂量信息。利用计划相减的办法,得到在某一具体空间坐标处(即患者体内某一确定位置)的两种剂量计算差异。

5.统计学处理:数据以 ± s表示。采用SPSS 19.0软件分别对Dw和Dm两组剂量信息进行配对t检验。P < 0.05为差异有统计学意义。

结 果

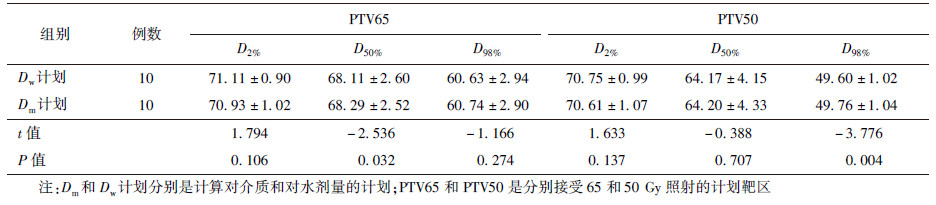
1. 靶区剂量: 10例患者MC算法计算靶区的两组剂量结果列于表1。靶区PTV65和PTV50的D50%、D98%和D2%的两种计算剂量的平均差异分别为:-0.3%、-0.2%、0.3%和0.1%、-0.6%、0.4%。从表1的结果可以得出,在Dm和Dw的差异中,PTV65的D50%和PTV50的D98%差异有统计学意义(t =-2.536、-3.776,P < 0.05),其余的剂量体积参数差异无统计学意义(P>0.05)。所有靶区剂量体积参数的偏差结果都在1%以内。

表 1 10例肺癌患者蒙特卡罗算法计算靶区的Dw与Dm的剂量（Gy, ± s）

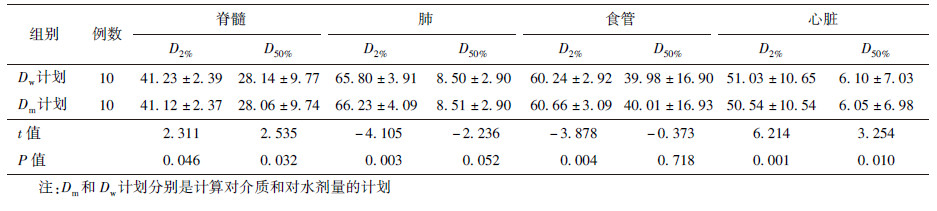
2. 正常组织剂量:10例患者的正常组织的剂量体积参数结果列于表2。正常组织的中位剂量D50%中,脊髓、心脏、肺和食管的Dm与Dw的平均偏差为0.3%、1.1%、-0.2%和-0.1%;对近似最高剂量D2%,脊髓、肺、食管和心脏的两种计算剂量的平均偏差为0.3%、-0.6%、-0.7%和0.6%。在正常组织D50%的中位剂量中,脊髓和心脏的Dm比Dw稍低(t=2.535、3.254,P < 0.05),肺和食管的Dm比Dw高0.2%和0.1%,差异无统计学意义(P＞0.05)。对正常组织的D2%,脊髓、肺、食管、心脏的Dm和Dw的差异有统计学意义(t=2.311、-4.105、-3.878、6.214,P < 0.05)。通过计算可以得出,所有剂量体积的偏差均＜2%。

表 2 10例肺癌患者正常组织的Dw与Dm剂量参数比较（Gy, ± s）

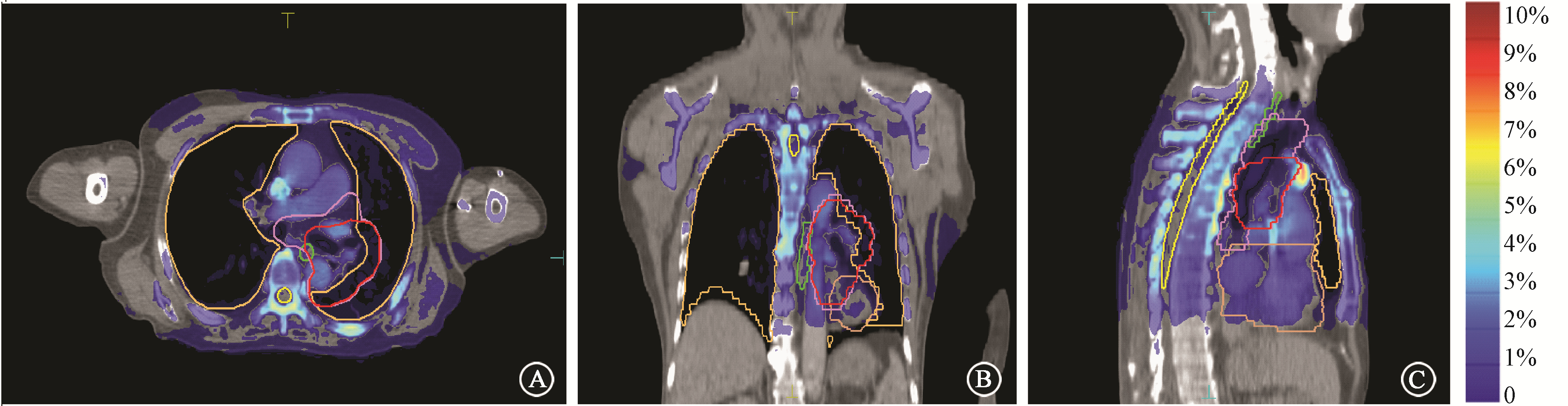
3. 剂量差异分布:两种计算剂量的差异在某一例患者体内三维空间分布如图1所示。从剂量差异结果的3种层面分布上可以看出,高密度的骨性结构的位置,两种剂量的差别通常比较大,一般有5%以上,而软组织的两种计算剂量差别则相对要小一些( < 2%)。

图1 1例患者的Dw与Dm剂量差异在空间3个层面上的分布情况 A.横断面；B.冠状面；C.矢状面
讨 论

MC算法的剂量计算依赖于所调用的物质截面数据库,不同组织介质、水介质的作用截面数据并不严格一致,对本研究所涉及的6 MV X射线能量,软组织的作用截面与水很接近,所以,对两种介质的计算剂量结果差异小;而对于高密度骨组织,两者所用截面的差异变大,结果差异明显。Monaco的MC算法对肺癌患者计算的结果也证实了这点:对临床勾画的靶区和正常组织,Dm与Dw差异不明显,偏差均在2%以内;而在没有勾画出的一些骨性区域,两种剂量相差甚至>5%。在MC算法的应用中,放射治疗的剂量报告应该使用对水的吸收剂量还是使用对介质的吸收剂量是一个争论的话题[6]。支持使用Dw的一方认为,TPS建立机器模型的数据是在水中测量的,输出量的校准规程也使用的是对水的剂量,临床的经验也是基于对水的吸收剂量。而支持使用Dm的一方则认为,Dm代表了介质体积位置处的剂量,是真正意思上的吸收剂量,是MC算法的优势,同时使用因子转换成Dw也会引入一定的不确定性。目前,非MC算法(卷积叠加、笔形束等)的TPS计算的一般都是对水的剂量。不管TPS的剂量报告采用的是何种剂量,在临床使用的时候,两种剂量的差别一定要清楚。

在一些特别的情况下,需要关注骨性组织的剂量。比如骨转移病灶,肿瘤位于骨性组织位置,或者计划设计时需要限制骨性组织的高剂量。此时,使用计算对介质剂量的TPS需要特别注意,因为,其剂量结果转换到对水的剂量后会明显大很多[7],有必要对其剂量做一定比例的预设或转换。一般情况下,IMRT计划都要通过测量验证后才能进行治疗。本研究结果也显示了两种剂量的系统性差异,如果测量采用的是均匀等效水模体,Dm和Dw计算的差别基本可以忽略。但如果使用的是不均匀模体,包含高密度的材料,两种剂量的差别可能会对最终的剂量验证通过率有一定的影响。Kan等[12]的研究数据结果显示,对鼻咽癌调强计划,使用不均匀的调强验证模体(包含高密度的类骨性材料),TPS计算的对介质剂量与对水剂量计划的验证通过率存在一定的差异。

综上所述,对肺癌患者的MC计算表明,对介质的剂量和对水的剂量存在一定的差异,靶区和正常组织剂量参数的偏差＜2%,对没有勾画出的骨性区域,两种剂量的差异会＞5%,在临床应用中应引起足够注意。而在进行计划验证时,更要注意根据所使用的验证模体(均匀与非均匀)来选择Dm还是Dw,由于通常测量的剂量都是基于对水的吸收剂量,因此,本研究推荐使用Dw,以得到更接近实际的剂量结果。

参考文献
[1] Papanikolaou N, Battista J, Boyer A, et al. AAPM report No 85: tissue inhomogeneity corrections for megavoltage photon beams[R]. Madison, WI: Medical Physics Publishing, 2004:1-135.
[2] [ZK(]Fogliata A, Nicolini G, Vanetti E, et al. The impact of photon dose calculation algorithms on expected dose distributions in [LL]lungs under different respiratory phases[J]. Phys Med Biol, 2008, 53(9): 2375-2390.
[3] Hartmann-Siantar CL, Walling RS, Daly TP, et al. Description and dosimetric verification of the PEREGRINE Monte Carlo dose calculation system for photon beams incident on a water phantom[J]. Med Phys, 2001, 28(7): 1322-1337.
[4] Mika S, Christ G. Experimental validation of a Monte Carlo-based treatment-planning system for electron beams[J]. Strahlenther Onkol, 2007, 183(3): 150-156.
[5] Li J, Doemer A, Harrison AS, et al. Dose calculation using Monte Carlo algorithm of Monaco treatment planning system[J]. Int J Radiat Oncol Biol Phys, 2008, 72(1 Suppl): S674.
[6] Keall P. Dm rather than Dw should be used in Monte Carlo treatment planning. Against the proposition[J]. Med Phys, 2002, 29(5):923-924.
[7] Siebers JV, Keall PJ, Nahum AE, et al. Converting absorbed dose to medium to absorbed dose to water for Monte Carlo based photon beam dose calculations[J]. Phys Med Biol, 2000, 45(4): 983-995.
[8] Edge SB, Byrd DR, Compton CC, et al. AJCC cancer staging manual[M]. 7thed. New York: Springer, 2010: 253-270.
[9] International Commission on Radiation Units and Measurements. ICRU report 50: prescribing, recording, and reporting photon beam therapy[R]. Bethesda, MD: ICRU, 1993.
[10] International Commission on Radiation Units and Measurements. ICRU report 62: prescribing, recording and reporting photon beam therapy (supplement to ICRU report 50)[R]. Bethesda, MD: ICRU, 1999.
[11] International Commission on Radiation Units and Measurements. Report 83: Prescribing, recording and reporting photon-beam intensity-modulated radiation therapy(IMRT)[J]. Bethesda, MD: ICRU, 2010.
[12] Kan MW, Leung LH, So RW, et al. Experimental verification of the Acuros XB and AAA dose calculation adjacent to heterogeneous media for IMRT and RapidArc of nasopharygeal carcinoma[J]. Med Phys, 2013, 40(3): 1-19.