2. 中山大学肿瘤防治中心肿瘤放疗科
在肿瘤精确放射治疗中,放射治疗计划系统剂量计算方法的精度直接影响到肿瘤靶区与正常组织的剂量分布,对治疗的成败起到关键性的作用。由于人体胸部解剖构成的特殊性,包含肺组织、骨组织以及不规则空腔结构,不同的计算方法在非均匀组织中剂量计算精度误差较大[1, 2, 3],是精确放射治疗的关键问题。在非均匀介质的处理过程中,蒙特卡罗方法是剂量计算的常用算法[4, 5, 6],但计算速度慢。有限笔形束算法(FSPB)在非均匀介质中密度变化较大时,计算仍存在一定的误差[7]。Fippel[8]开发了快速X射线体积元蒙特卡罗算法(XVMC),使计算时间有一定程度的缩短。本研究基于瑞典Elekta公司的MONACO的两种计算模型在非均匀组织条件下对规则照射野和调强放射治疗射野的剂量准确性进行验证。
1. 材料与设备:选用瑞典Elekta公司的MONACO3.0调强放射治疗计划系统。美国ARTM公司型号为1051的仿真人型模体由含有骨组织密度、肺组织密度、空气腔以及等效固体水组成,每层厚度均为2.5 cm,其中有等效软组织材料物理密度为1.06 g/cm3,肺等效材料物理密度为[JP]0.28 g/ cm3,骨等效材料物理密度为1.68 g/cm3。美国ISP公司生产的EBT2胶片剂量分析系统由三部分构成,包括EBT2胶片(美国 ISP公司,编号A03301102,有效日期至2016年3月)、彩色平板扫描仪(美国EPSON公司 perfection v750 pro)、剂量分析软件(美国FilmQA公司型号v 2.2)。美国GE公司 Speed Light大孔径CT模拟定位机及Advantage SIM4.2工作站;美国Varian23EX直线加速器,光子射线能量为6和15 MV。
2. 胶片剂量验证系统:按文献[9]方法,利用FilmQA v 2.2软件把曝光后的放射性铬胶片进行扫描分析。输入对应的机器跳数(MU),形成胶片剂量响应曲线,并刻度胶片的绝对剂量。曝光后放置2 h,利用彩色平板扫描仪扫描胶片形成tif格式文件,扫描参数色彩为48位、分辨率75 dpi。
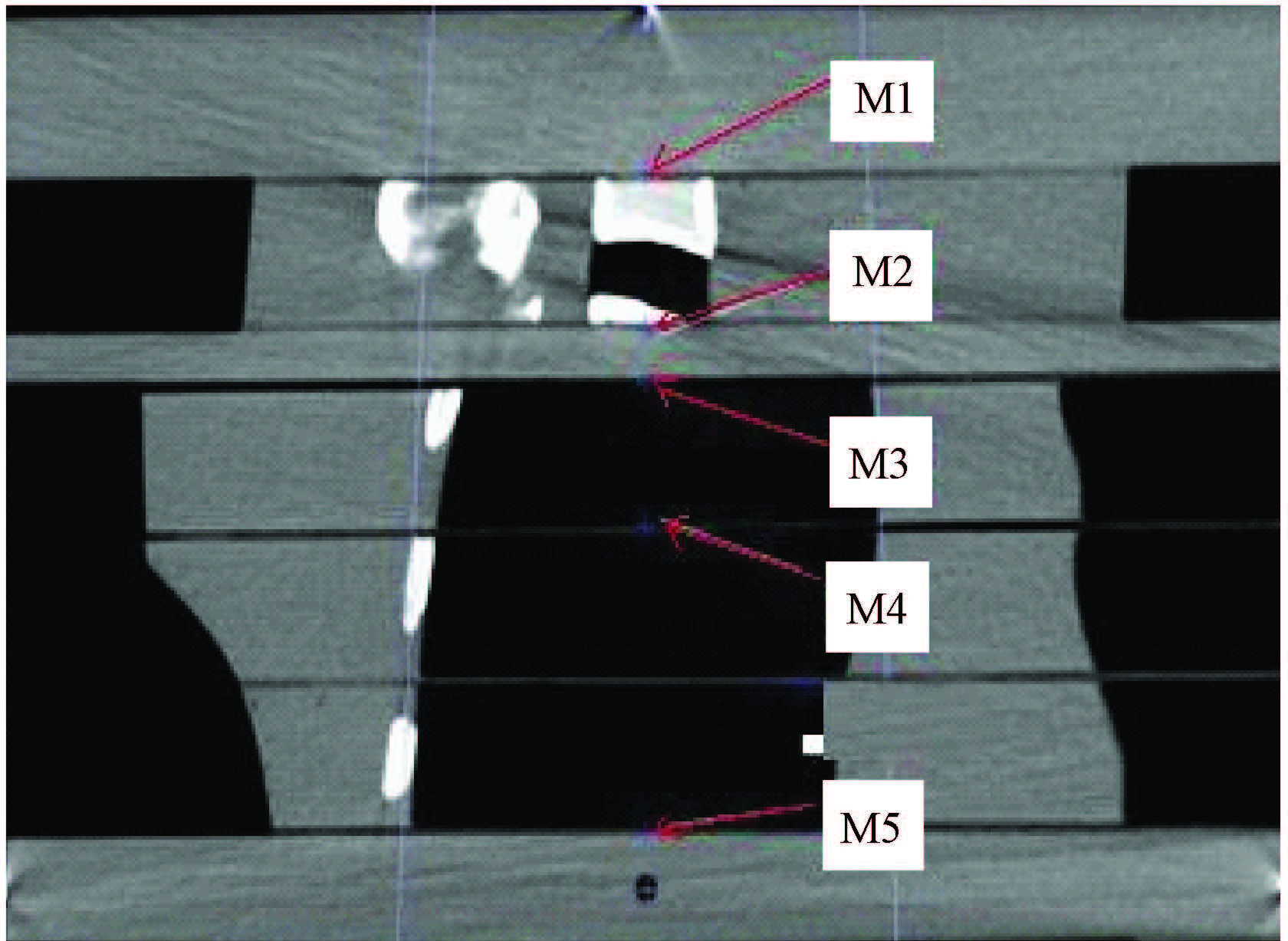
3. 混合介质模体CT图像扫描及感兴趣点的选取:取仿真人型模体中胸部模体层面,含有肺组织、骨组织及空腔的层面模体建立非均匀性的模体,如图1所示。在GE speed light大孔径CT模拟定位机下扫描,扫描条件:螺旋扫描层厚2.5 mm、螺距0.75、电压120 kV、电流160 mA,扫描后将图像输出并导入MONACO计划系统。在非均匀模体中选取不同介质交界面的感兴趣点,感兴趣点的位置如图1中红色箭头所示的界面,这些感兴趣点依次分别位于水-骨(M1)、骨-水(M2)、水-肺(M3)、肺-肺(M4)、肺-水(M5)等不同密度组织界面。
|
图1 混合介质模体及剂量感兴趣点 注:水-骨(M1)、骨-水(M2)、水-肺(M3)、 肺-肺(M4)、肺-水(M5)等不同密度组织界面 |
4. 规则射野的两种算法剂量测量:在非均匀模体中,利用EBT2胶片剂量验证系统,对规则照射野的两种算法计算结果进行对比,将EBT2胶片剪为10 cm×10 cm的小胶片,标记出每张小胶片的中心测量点,物理参数条件:X射线能量6和15 MV,射野大小分别为10 cm×2 cm和10 cm×10 cm,200 MU,源皮距(SSD)90 cm。将EBT2胶片放在感兴趣点相应的层面中心,进行剂量测量,重复测量3次,结果取平均值,利用FilmQA v 2.2软件进行分析,并分别与两种不同算法的计算结果比较。
5. 调强射野的两种算法剂量测量:在仿真人型模体中,从MONACO治疗计划系统中选取食管癌的调强治疗计划(IMRT)滑窗技术治疗模式照射野10个,X射线 6 MV。将IMRT的照射野角度全部归零后移植于仿真人型的胸部模体中,重新计算仿真人型模体中的剂量分布,剂量计算允许的误差设为1%、计算网格设为3 cm×3 cm,分别输出EBT2胶片层面的二维平面剂量图,并与相应层面EBT2胶片实际测量的二维平面剂量进行比较分析。分析方法包括γ(3%/3 mm)通过率分析、水平方向以及垂直方向的等剂量曲线分析。
6. 统计学处理:数据以 ±s表示,采用SPSS 13.0统计软件分析数据。
±s表示,采用SPSS 13.0统计软件分析数据。
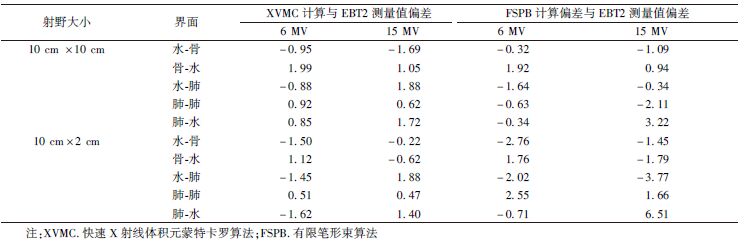
1.规则照射野结果分析:在非均匀模体中,规则照射野计算结果与测量结果分析,结果列于表1。MONACO计划系统中XVMC算法在能量为6和 15 MV光子线的非均匀模体规则照射野的实验组中,其计算的不同深度,不同组织界面的剂量结果与EBT2胶片测量的结果相符,偏差在±2%以内。在6 MV、射野大小分别为10 cm×2 cm、10 cm×10 cm以及15 MV、射野大小为10 cm×10 cm的实验组中,FSPB算法的结果与EBT2胶片的测量结果较符合,偏差在±3%以内,较XVMC的算法与EBT2胶片的结果符合度稍差;而15 MV、射野大小为10 cm×2 cm的计算结果,在肺内的计算结果高于EBT2胶片测量结果,在肺-水界面高达6.51%。
| 表1 不同能量射线在两种射野下测量值与两种算法计算偏差(%) |
2.IMRT照射野结果分析:仿真人型模体中,在离胸壁前缘深度6 cm处胸腔内取水平方向的胶片剂量响应曲线,XVMC算法计算出的剂量曲线均与EBT2测量的结果基本吻合。而FSPB算法计算出的结果在射野内高剂量区较EBT2胶片测量的结果要高,偏差为在3%~4%之间。垂直方向的胶片剂量响应曲线,y轴坐标正方向表示射野入射方向。XVMC算法计算出的剂量曲线均与EBT2胶片测量的结果较吻合,偏差均<2%。而FSPB算法计算出的结果较EBT2胶片测量的结果偏差达4%。
3.IMRT照射野下两种算法与胶片测量结果的γ指数分析比较:对10个6 MV能量的X射线IMRT计划射野的剂量分布,与EBT2胶片测量结果比较,XVMC算法计算结果的γ (3 mm,3%)通过率为94.90%±1.23%;而FSPB算法计算结果通过率则为82.89%±1.78%,后者的计算精度明显差于前者。放宽评价标准后FSPB算法的γ(4 mm,4%)通过率为91.95%±2.35%。
目前对IMRT计划剂量验证结果仍然没有一个统一的评估标准,临床上普遍采用国内外经验式推荐的方法来判断剂量验证的结果。国际辐射单位与测量委员会(ICRU) 24号报告指出[10],3%剂量计算误差将导致放射治疗总的不确定度达到4.3%甚至更高达5%,其中包括系统误差及摆位误差。为了使总的不确定度控制在±5%之内,在进行三维治疗计划剂量计算时必须控制剂量误差在±3%范围之内,甚至更低的剂量误差,以提高肿瘤控制率并减小正常组织并发症概率。EBT2胶片测量方法在临床上已经得到广泛应用,其测量结果的可靠性也得到国内外专家的认可[9, 11, 12, 13]。
从EBT2胶片测量结果来看,在非均匀模体中,MONACO计划系统中利用XVMC算法计算不同能量射线的规则照射野与IMRT照射野的结果与EBT2胶片测量的结果误差较小,在剂量学方面均能达到临床的要求。由于蒙特卡罗方法能在非均匀介质中模拟光子的输运过程,与介质相互作用后所产生的次级电子的能量沉积,并考虑了电子失衡对剂量的影响,从而剂量计算结果误差较小,能满足临床上不同能量不同大小照射野的剂量学要求。FSPB算法是基于电子平衡的条件下的一种算法,但是在非均匀介质中密度变化较大时,高能射线计算仍存在很大的误差[14, 15]。光子与含有低密度肺组织的非均匀模体相互作用后产生的次级电子,当光子能量较小时,其产生的次级电子射程较短,并向侧向散射,如果照射野足够大时,达到电子平衡,射野内的能量沉积越多,其计算的结果误差越小。如实验中FSPB算法在6 MV能量的X射线情况下,规则照射野计算结果与EBT2胶片结果误差在±3%范围之内,其中10 cm×10 cm照射野测量结果优于10 cm×2 cm照射野的测量结果,射线能量较小时基本能满足临床剂量学要求。当入射光子能量为15 MV时,其产生的次级电子射程较长,照射野较小时产生侧向电子失衡,使射野内的吸收剂量减小,局部导致较大剂量误差。当失去电子平衡的条件下,FSPB算法仍然按照电子平衡的条件进行剂量计算,这将导致局部剂量计算结果高于实际EBT2胶片测量结果。本研究实验结果中FSPB算法在15 MV能量下的10 cm×2 cm照射野在肺-水界面计算结果比EBT2胶片测量结果高出6.51%,这一结果与之相符合。相关报道,傅卫华等[16]分析了肺部肿瘤高能X射线放射治疗计划采用笔形束算法计算,误差高达18%。临床IMRT计划中含有大量的条带状的小子野,同样可能存在电子失衡条件的情况,本研究6 MV能量的X射线IMRT实验组中使用FSPB算法进行计算,在胸腔内不均匀的肺组织吸收剂量误差最高达4%、γ指数分析3%/3 mm条件下通过率未能达到90%,观察其未通过的剂量点大部分落在肺组织内,考虑为由于FSPB算法在非均匀介质中计算所导致的误差。在IMRT照射野中另外观察到一小部分射野未能通过γ指数分析的剂量点位于射野外边缘处,通过人工移位1 mm再进行比对,原边缘处未通过的剂量点在3%/3 mm的条件下通过亦超过90%,这部分误差考虑由于摆位误差的原因所致。
综上所述,由于人体组织结构的复杂性,在组织不均匀条件下,由于IMRT计划中存在着许许多多的小子野,如果使用高能X射线进行计划设计时,更加容易出现侧向电子失衡的现象。所以在临床应用中,特别是胸部肿瘤以及密度变化比较大的部位,应该充分考虑XVMC算法计算不均匀组织剂量的准确性以及FSPB算法的缺点,避免由于射线能量及算法选择不当的原因所致的计划靶区剂量缺失的情况出现。
| [1] | Fotina I, Winkler P, Künzler T, et al. Advanced kernel methods vs. Monte Carlo-based dose calculation for high energy photon beams[J]. Radiother Oncol, 2009, 93(3): 645-653. |
| [2] | Kragl G, Albrich D, Georg D. Radiation therapy with unflattened photon beams: dosimetric accuracy of advanced dose calculation algorithms[J]. Radiother Oncol, 2011, 100(3): 417-423. |
| [3] | Zarza-Moreno M, Carreira P, Madureira L, et al. Dosimetric effect by shallow air cavities in high energy electron beams[J]. Phys Med, 2014, 30(2): 234-241. |
| [4] | Altunbas C, Kavanagh B, Dzingle W, et al. Dosimetric errors during treatment of centrally located lung tumors with stereotactic body radiation therapy: Monte Carlo evaluation of tissue inhomogeneity corrections[J]. Med Dosim, 2013, 38(4): 436-441. |
| [5] | Mampuya WA, Matsuo Y, Nakamura A, et al. Differences in dose-volumetric data between the analytical anisotropic algorithm and the x-ray voxel Monte Carlo algorithm in stereotactic body radiation therapy for lung cancer[J]. Med Dosim, 2013, 38(1): 95-99. |
| [6] | Bueno M, Paganetti H, Duch MA, et al. An algorithm to assess theneed for clinical Monte Carlo dose calculation for small proton therapy fields based on quantification of tissue heterogeneity[J].Med Phys, 2013, 40(8):081704. |
| [7] | Jeleń U, Alber M. A finite size pencil beam algorithm for IMRT dose optimization: density corrections[J]. Phys Med Biol, 2007, 52: 617-633. |
| [8] | Fippel M. Fast Monte Carlo dose calculation for photon beams based on the VMC electron algorithm [J]. Med Phys, 1999, 26(8):1466-1475. |
| [9] | Chang L, Ho SY, Ding HJ, et al. Dependency of EBT2 film calibration curve on postirradiation time[J]. Med Phys, 2014, 41(2): 021726. |
| [10] | Shalek RJ. Determination of absorbed dose in a patient irradiated by beams of X or γ rays in radiotherapy procedures[J]. Med Phys, 1977, 4(5):461. |
| [11] | Hu Y, Wang Y, Fogarty G, et al. Developing a novel method to analyse Gafchromic EBT2 films in intensity modulated radiation therapy quality assurance[J]. Australas Phys Eng Sci Med, 2013, 36(4): 487-494 |
| [12] | Butson MJ, Yu PK, Cheung T, et al. High sensitivity radiochromic film dose comparisons[J]. Phys Med Biol, 2002, 47(22): N291-295. |
| [13] | 周颖娟, 黄劭敏, 邓小武.辐射显色剂量胶片的特性及其在放射医学的应用[J].国际肿瘤学杂志,2007,34(1) : 28-31. |
| [14] | Carrasco P, Jornet N, DuchMA, et al. Comparisonof dose calculation algorithms in phantoms with lung equivalent heterogeneities under conditions of lateral electronic disequilibrium[J]. Med Phys, 2004, 31(10): 2899-2911. |
| [15] | Jones AO, Das IJ. Comparison of inhomogeneity correction algorithms in small photon fields[J]. Med Phys, 2005, 32(3): 766-776. |
| [16] | 傅卫华, 胡逸民, 戴建荣. 侧向电子失衡对肺部肿瘤放射治疗计划设计的影响[J].中国生物医学工程学报,2004,23(1): 49-54. ) |
 2015, Vol. 35
2015, Vol. 35